基于区间摄动的不确定非线性结构动力学模型修正方法研究

任铭泽，邓忠民，国兆普

(1.北京航空航天大学 宇航学院，北京 100191；2.中国航天科工集团 北京动力机械研究所，北京 100074)

近年来，有限元模型修正方法被广泛应用于航空、航天、土木建筑等领域[1]，这类方法利用测量数据作为参考数据来提高模型精度，通过识别和改进建模参数，从而使模型能更好地对结构的响应进行预测[2]。

确定性结构有限元模型修正方法[3-4]目前已被广泛应用于工程结构中，但在实际工程结构中普遍存在不确定性[5]。工程中的不确定性主要分为三类[6]：①结构参数不确定性，例如某些复合材料的物理参数存在明显不确定，螺栓、铰接等连接结构的边界条件难以精准化等；②分析模型不确定性，主要是由仿真软件本身的边界条件难以精准化等；③试验测量不确定性,例如在测量过程中，由于人为或者仪器本身误差导致的不确定性。结构不确定性在很大程度上影响动力学分析结果的可信度，因此开展考虑不确定性的结构有限元模型修正的研究具有极大的工程意义。

不确定性研究方法主要分为概率与非概率方法[7]。概率方法通常需要大量的试验数据来获得较准确的统计信息，但是当试验数据样本数量较少，不足以准确的描述结构的统计特性时，会引起较大的误差[8]。非概率方法中具有代表性的就是区间方法，仅需要参数的上下界即可进行相关研究，对于处理少量试验数据或某些特殊的不确定性问题有很好的效果。得益于区间理论的发展以及Chen等[9]、Ben-Haim等[10]学者的研究，区间方法已成功应用于结构静力学、动力学分析问题。

在不确定性有限元模型修正研究领域，Collins等[11]首先提出的最小方差法；之后，Beck等[12]提出了贝叶斯统计框架，利用动态响应数据定量分析结构模型的预测精；王登刚等[13]提出了一种结构计算区间反演方法，将模型修正问题转化为全局优化问题；姜东等[14]提出了在区间参数结构特征值分析理论基础上，利用参数灵敏度分析进行区间模型修正方法。

线性结构的不确定问题研究已经取得很大成果，非线性结构与线性结构相比，非线性结构的响应与输入之间的传递函数会随着激励的变化而变化，因此非线性响应的求解往往会有更大的计算量甚至会有收敛性问题。在不确定非线性分析研究上，张义民等[15]提出了一种概率摄动有限元法，并用于解决多自由度非线性随机参数振动响应分析，但是此方法对参数先验信息要求较高；邱志平等[16]采用一种以区间数学为基础,将不确定性参数用区间进行定量化,借助一阶泰勒级数,给出了近似估计非线性振动系统动力响应范围的区间分析方法，相较于概率摄动法结果略显保守。已有的非线性动力学研究主要集中在研究已知不确定参数的区间分布信息，对参数的响应区间的求解问题上，对不确定非线性模型修正问题还缺少相关的研究。

本文介绍了一种区间模型修正法，它是一阶区间摄动技术与传统的有限元模型修正中代价函数相结合的产物。传统的有限元模型修正问题将仿真响应与实际响应的差的平方和作为优化的目标函数，本文基于传统模型修正方法，结合区间摄动理论，进行不确定性模型修正问题中非概率区间模型修正问题研究，相较于以往不确定非线性分析研究，降低了对参数区间分布的先验信息需求的同时，研究通过区间摄动法求解响应区间，并在此基础上对不确定参数区间进行修正。

1 相关理论

1.1 非线性结构动力学区间摄动理论

考虑N自由度非线性结构系统动力学微分方程

(1)

式中，B为不确定性参数，可以包含不确定载荷参数和不确定结构参数。

(3)

式中，Kc为非线性刚度系数，用于描述非线性恢复力，Kc通常用非线性系数c乘以结构不确定刚度K来表示。

采用区间摄动理论将其分解为区间均值和区间半径两部分

K=[Kc-ΔK,Kc+ΔK]

(4)

式中：Kc为区间均值；ΔK为区间的半径。

对含不确定参数的非线性结构时域响应，相应地有

X(t)∈X(t)I=[X0-ΔX,X0+ΔX]

(5)

对于自由度为N的系统有X=[X1,X2,…，Xn]

X的区间均值为

(6)

式中，s为样本点数量。

区间半径为

(7)

时域动响应分解为

(8)

1.2 基于区间摄动的模型修正理论

定义目标函数

minr(B)=(Xi(B)-Xi)2

(9)

式中：Xi(B)为仿真值;Xi为真实值。将不确定参数定义为确定部分和不确定小量的和的形式

B=Bc+δB

(10)

与此同时将响应也分为确定参数和不确定参数两部分的响应

(11)

相应的将优化的目标函数分为由确定参数(区间均值)和不确定参数(区间半径)导致的响应两部分的和的形式

r(B)=r0(Bc)+δr(δB)

(12)

将式(8)、式(11)、式(12)代入式(9)

(13)

式(13)展开并分离为确定参数部分零阶式的式(14)和不确定参数部分一阶式的式(15)

(14)

(15)

(16)

通过求解式(14)中的极小化问题，可以得到不确定参数均值的估计。现在的主要目标是找到求解参数的“真”区间半径，使结构响应的修正值与试验值相匹配，用ΔXi近似替换式(16)中的δXi作为真实响应的区间半径，得到

(17)

通过建立和求解式(14)和式(17)的最小值问题。可以得到不确定参数的修正区间，并用均值和区间半径区间来表示。通过上述分析，区间有限元模型修正过程主要包括两个步骤：①区间均值优化；②在均值修正基础上，区间半径优化。

2 模型修正算法

2.1 区间均值修正

区间均值的修正问题，与确定性模型修正问题类似，可分为以下几步：

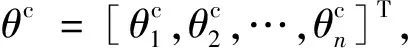
步骤2代入结构动力学时域动响应计算的算法中，得到时域响应的区间均值的X0(θc)，建立参数区间均值和响应区间均值的函数关系

(18)

步骤3利用式(14)得到待修正参数的确定部分(区间均值)导致的响应的与试验数据的残差

ε1=X(θ0)-Xm

(19)

步骤4将均值的修正转化为了如下的优化问题

(20)

式中,下标l和u分别为修正参数的空间的下限和上限，通过对式(20)进行最小化寻优可得到参数的均值的修正值

θc=[θ1c,θ2c,…,θnc]T

(21)

2.2 区间半径修正

区间半径的修正算法主要有以下几个步骤：

步骤1在区间均值修正的基础上，基于对待修正参数区间采用固定抽样间隔的均匀抽样方法得到样本点，代入有限元模型计算得到时域响应区间；

步骤2建立参数区间半径和响应区间半径的函数关系

δX=δX(δθ)=[δx1(δθ),δx2(δθ),…,δxn(δθ)]T

(22)

其中,

(23)

(24)

步骤3利用式(17)得到待修正参数不确定部分(区间半径)导致的响应的与试验数据区间半径的残差

ε2=δX(δθ)-ΔXm

(25)

步骤4因此将区间半径的修正转化为了如下的优化问题

(26)

步骤5通过对式(26)进行最小化寻优可得到参数的区间半径的修正值

Δθ=[δθ1,δθ2,…,δθn]T

(27)

步骤6因此待修正参数区间的修正值为

Θ=[θc-Δθ,θc+Δθ]

(28)

具体流程如图1所示。其中区间均值修正步骤中，均值附近的固定取样区间设定为真实区间半径，灰色部分为真实的区间信息。可以看出算法分为两步：①求解区间均值修正值；②在此基础上，修正摄动量(区间半径)，这保证区间半径是在区间均值修正基础上的的修正结果，这是两个相关联的变量。

图1 基于摄动法的区间模型修正流程

3 算例分析

3.1 算例一 两自由度刚架结构

算例模型采用如图2所示的两层刚架结构，钢架结构的支柱只提供弯曲刚度不计质量，水平杆具有质量，只发生水平位移，系统的运动微分方程为

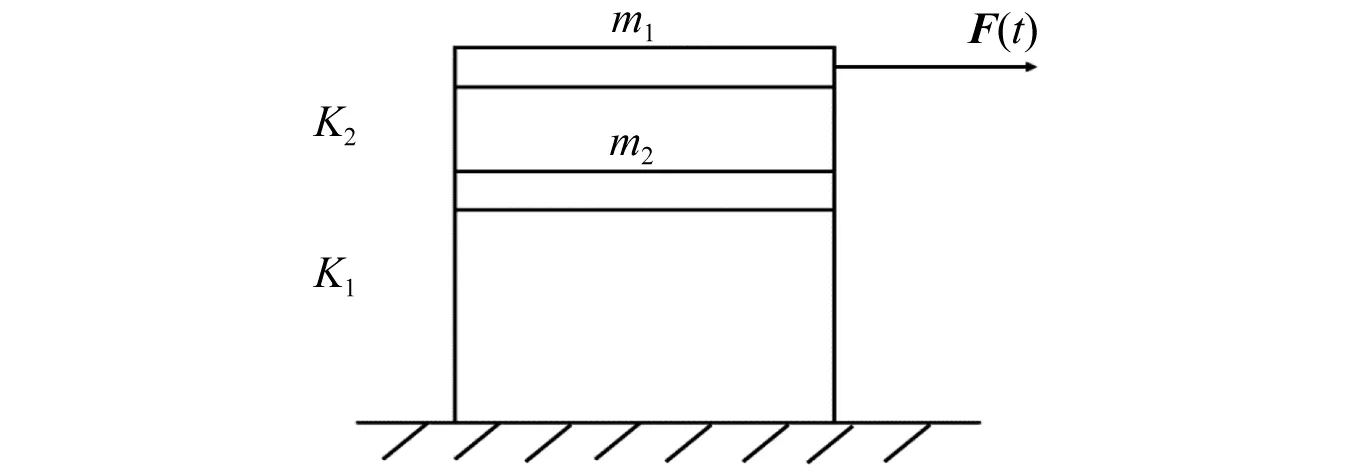
图2 两自由度刚架结构

(29)

其中,

Kc=c×K×104

(30)

确定的结构参数包括刚架m1,m2质量分别为1 kg，2 kg，等效非线性系数为Kc，其中c分别取0和1，对比分析线性和非线性模型修正方法的修正效果，外作用力F(t)=10·sin(100·t)。

假设不确定的参数真实值区间为

K1=K2=[0.8,1.2]·103N/m。

区间均匀抽样的取样间隔r分别设定为0.01和0.001，样本点个数由区间长度除以取样间隔r得到。时域动响应的计算采用Newmark-β直接积分法，仿真时间为1 s，仿真步长为0.001 s。

分别假设待修正的参数的初始区间为

initial-1:K1=K2=0.9+[-0.4,0.4]·103N/m

initial-2:K1=K2=0.8+[-0.5,0.5]·103N/m

当非线性系数取0和1时，区间的均值和区间半径的迭代收敛曲线，如图3和图4所示。从图可知，区间均值和半径经过二十余次迭代后收敛到真实值附近，而且当初始区间不同的情况下，修正后参数区间均值和半径均能收敛到真实区间附近，这表明在非线性和线性不确定模型修正问题上，该算法具有很好的收敛效果，且算法稳定性好。c取0和1两种情况下修正前后参数的区间误差，如表1、表2和表3所示。从表中数据可知，两种结构形式下，修正后区间均值和区间半径的误差小于3%，较初始误差有大幅度下降，说明该方法对线性和非线性结构均有很高修正精度，表2和表3分别为不同取样间隔r为0.01和0.001的条件下，区间修正误差对比，结果表明取样间隔越小，修正后参数区间误差更小。

表1 修正前后不确定参数区间误差(c=0)

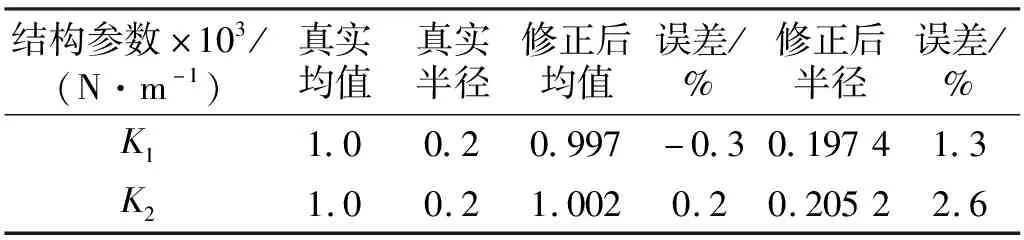
表2 修正前后不确定参数区间误差(c=1，initial-1,r=0.01)

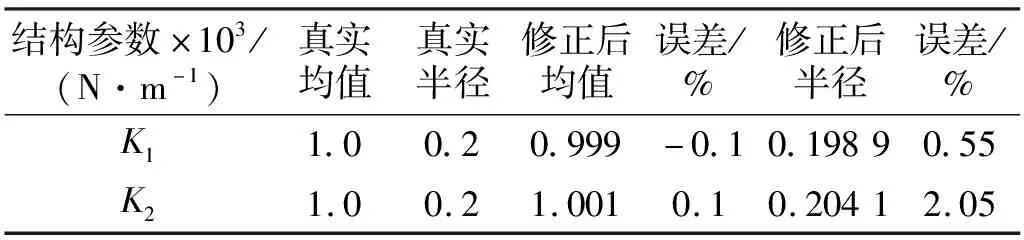
表3 修正前后不确定参数区间误差(c=1,initial-1,r=0.001)

图3 区间均值收敛过程

图4 区间半径收敛过程

对修正前后的参数区间，通过均匀取样的方法构造参数样本，带入确定的有限元模型计算得到修正前后的时域响应的区间分布。图5为(c=1，initial-1,r=0.001)条件下，修正前后自由度X2的时域响应的响应区间与真实的响应区间的对比，其中:U和 L分别为时域响应区间的上界和下界；R，Q，H分别为真实值、修正前和修正后。从图5可知，修正后的响应区间和真实的响应区间的曲线基本重合，两个区间在不同采样时间都能很好地吻合，能够准确反映仿真试验结果。

图5 修正前后时域响应X2(C=1, initial-1,r=0.001)

3.2 算例二 非线性悬臂梁

算例模型采用如图6所示的自由端带有非线性弹簧的悬臂梁结构，梁的截面为圆形,梁的结构参数如表4所示，以梁的材料的弹性模量E和材料密度ρ作为不确定参数的待修正参数。

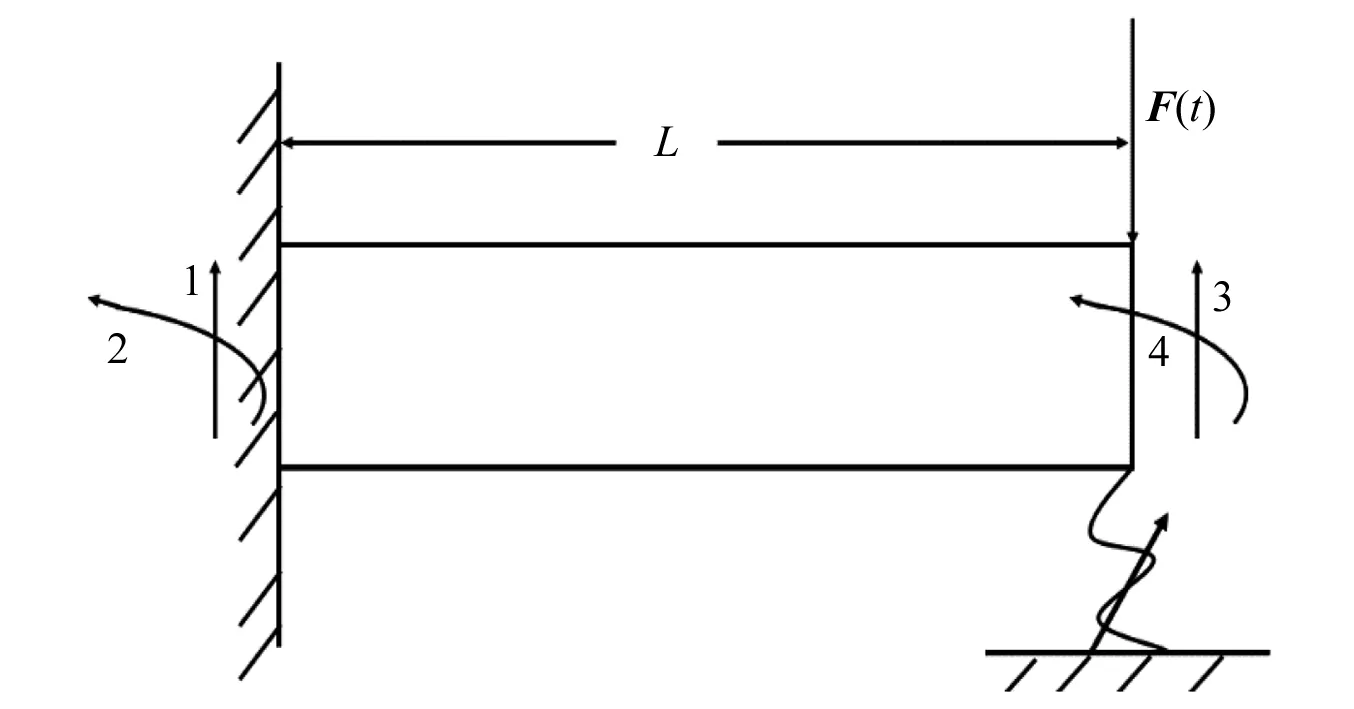
图6 悬臂梁有限元模型

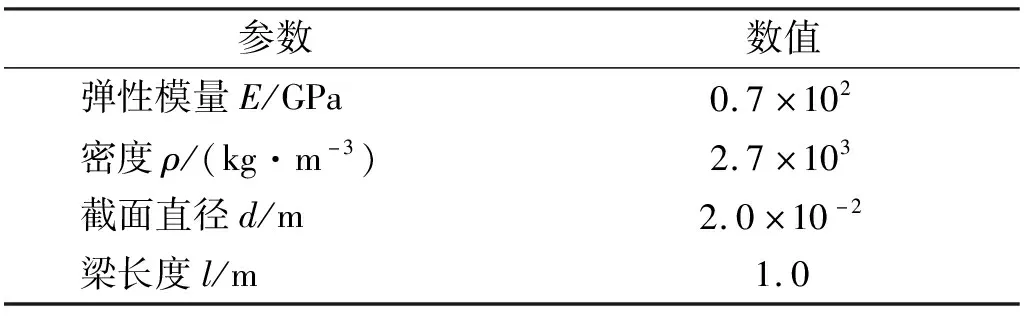
表4 梁结构参数

假设梁的材料特性参数中弹性模量E和材料密度ρ的真实值分别为

E=0.7+[-0.1,0.1](102GPa)

ρ=2.7+[-0.3,0.3](103kg/m3)

假设弹性模量E和材料密度ρ的初始值分别为

E=0.49+[-0.2,0.2](102GPa)

ρ=2.43+[-0.4,0.4](103kg/m3)

即弹性模量E的区间均值被低估了30%，区间半径初始误差+100%；材料密度ρ的区间均值被低估了10%，区间半径初始误差33.3%。

取立方非线性和分段非线性两种非线性形式进行仿真，对于立方非线性，非线性弹簧刚度系数Kc定义为k·c，c为非线性系数定义为1×103，弹簧恢复力位移呈现三次关系，结构的整体运动学方程为

(31)

对于分段非线性，取分段间隔|δ|=1×10-4，非线性恢复力呈现分段性，非线性恢复力为

(32)

结构运动学方程为

(33)

外力F(t)=600sin(400×t)，梁单元为欧拉-伯努利梁单元。采用Newmark-β法进行时域动响应的计算，取仿真时间t=5 s，时间步长为0.001 s。采用间隔r为0.001的均匀取样方法分别对初始和真实参数区间进行抽样，构造参数样本空间。

修正后不确定参数的区间误差比较，如表5和表6所示。非线性形式为立方非线性和分段非线性时，修正后参数的区间均值误差均下降到小于0.1%，弹性模量E区间半径误差从100%分别下降到1.4%和2.0%，材料密度ρ的区间半径误差下降到0.6%和0.8%。两种非线性形式下不确定参数的修正后误差与修正前相比均有大幅的下降。

表5 修正后参数的区间误差(立方非线性,r=0.001)

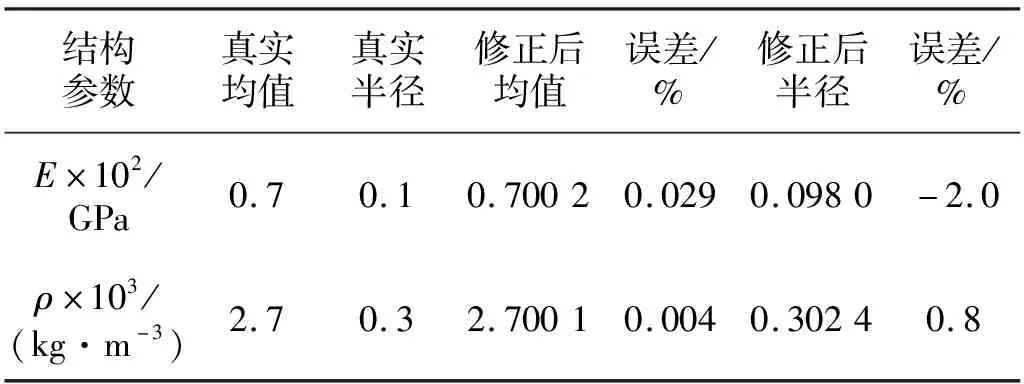
表6 修正后参数的区间误差(分段非线性,r=0.001)

弹性模量E和材料密度ρ的区间均值和区间半径的迭代收敛曲线(取样间隔r为0.001)，如图7和图8所示。从图中可以看出两种非线性形式的两个不确定参数的区间均值和区间半径在二十多次迭代后收敛于真实值附近。

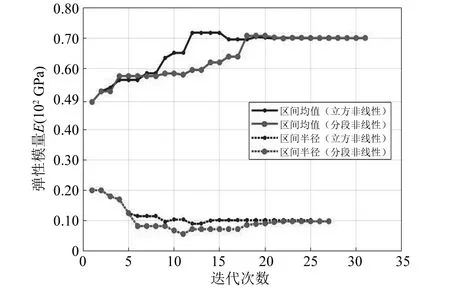
图7 弹性模量E收敛过程：区间均值，区间半径

图8 材料密度ρ收敛过程：区间均值,区间半径

为了直观对比修正前后的时域响应区间，分别计算参数修正前后以及试验(真实)的时域响应区间，修正前后的自由端的时域响应区间的修正值和试验值的对比，如图9所示。图9中的曲线代表的对象和“算例一”相同，从图中可以看出两种非线性形式下修正后的时域响应区间的上下界和真实的响应区间基本重合，证明两种非线性形式下修正后的响应区间都能反映真实的响应区间。

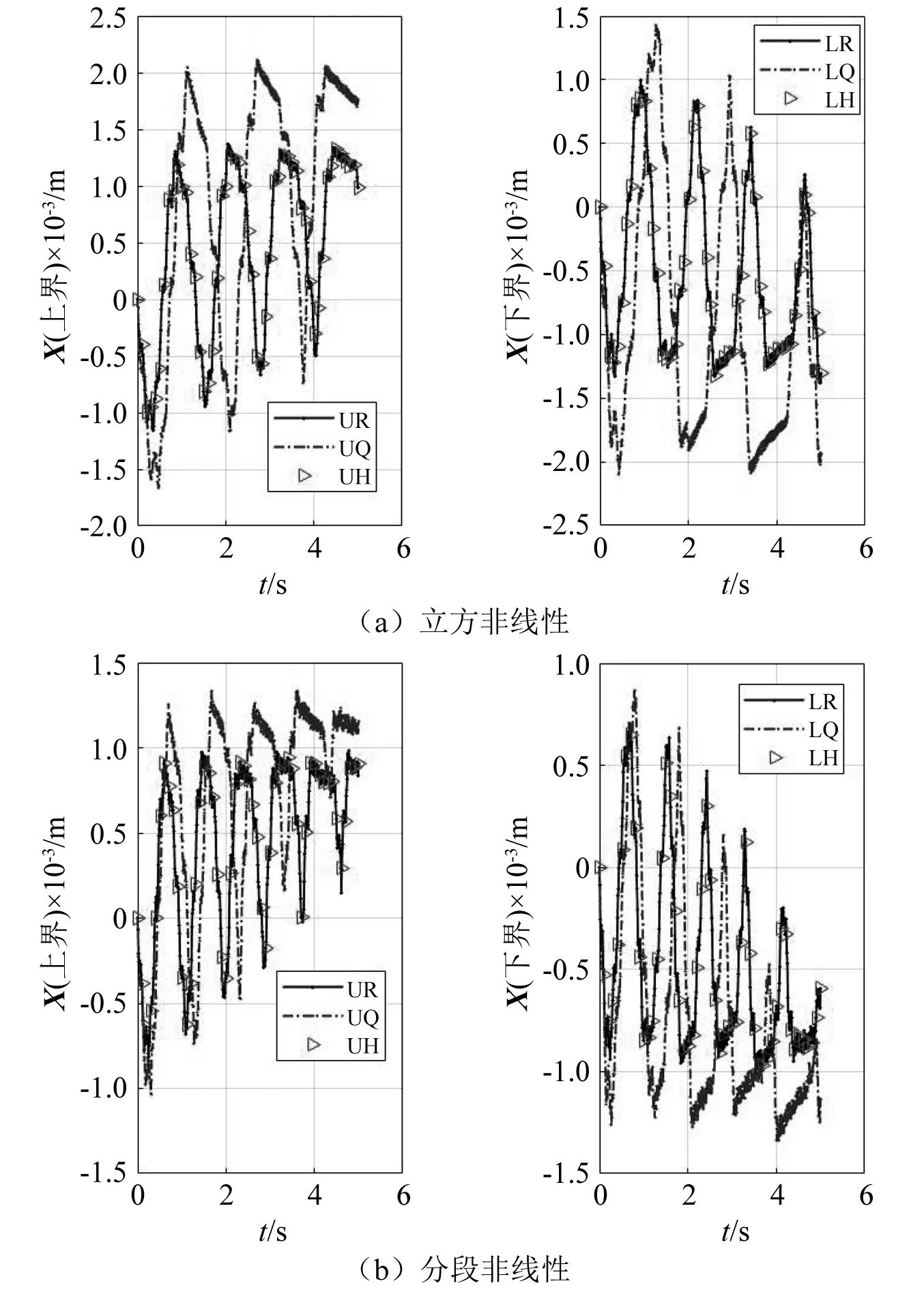
图9 修正前后时域响应区间

4 结 论

本文基于区间摄动原理，提出了一种求解不确定非线性结构模型修正问题的方法。通过区间摄动原理，将不确定性参数和时域动响应分别表示为区间均值和区间半径的形式。通过建立不确定参数和响应的区间均值、半径映射关系将不确定性模型修正问题转化为修正区间均值和区间半径的确定性优化问题。通过两种不同非线性形式以及潜在线性结构对比研究表明：

(1)立方非线性结构和潜在的线性结构的对比，两种情况下修正后不确定参数的修正误差均较小，说明此方法对非线性和线性结构都能适用。

(2)初始参数区间对算法修正结果影响较低，改变初始的参数区间，修正的区间参数仍能快速收敛，且修正后的结果具有很高的精度。

(3)立方非线性和分段非线性两种非线性结构的不确定参数的区间均值和区间半径都能快速的收敛到真实值附近，证明对于不同的非线性形式，该方法都能进行高效的区间修正。

根据修正后的区间构造参数样本，代入有限元模型中计算对应的响应区间，修正之后的响应区间与试验样本(真实值)的响应区间吻合良好，能够准确的反映试验样本的区间特性。