基于记忆多项式的时间交织模数转换器自适应非线性失配校正方法

刘素娟 张仲侯

(北京工业大学微电子学院 北京 100124)

1 引言

模拟数字转换器(Analog-to-Digital Converter,ADC)在现代电子系统中扮演着至关重要的角色，在各个领域都获得了广泛的应用[1-3]，高速、高分辨率是当今ADC的发展方向。然而，对于ADC来说，采样率和分辨率是一对相互制约的指标，由于制造工艺的限制，单个ADC很难同时满足高采样率和高分辨率的要求。文献[4]在1980年提出通过时间交织(time-interleaved)的方式对信号进行采样，即时间交织模数转换器(Time-Interleaved Analog-to-Digital Converter, TIADC)。从而可以在现有制造工艺的条件下，成倍地提高采样率。

由于器件制造工艺的非理想性，不可避免地会在通道之间引入失配误差，这些误差会降低TIADC的有效分辨率等动态性能[5,6]。在过去的几十年间，大量的学者对TIADC通道之间如增益失配误差、采样时刻失配误差、频率响应失配误差等线性失配误差的估计和校正方法进行了深入的研究[7-10]。近些年来，学者逐渐开始对TIADC中的非线性失配误差(nonlinear mismatch error)产生兴趣，非线性误差是由于模拟前端电路的非理想性、子ADC中的积分非线性以及微分非线性引入[11]，TIADC通道之间非线性的差异又会引起非线性失配误差。

很多学者对TIADC非线性失配误差进行分析并进行估计和校正[12-18]。文献[12,13]提出了一种通道随机化的校正策略，但是引入了额外的子ADC，增加了硬件资源消耗。文献[14,15]提出了一种基于Volterra级数的TIADC行为级模型，对TIADC的动态非线性失配误差进行建模并提出了一种适用于硬件实现的补偿结构。文献[16,17]提出了TIADC静态非线性失配误差的自适应校正算法，文献[16,17]均利用多项式模型对TIADC静态非线性失配误差进行建模，分别采用了带宽有效利用(Band Width Efficiency, BWE)和哈达玛调制的方法进行校正，并采取了滤波最小二乘的方法进行非线性失配误差的估计。文献[18]采用了简化的Volterra级数对双通道TIADC静态非线性失配误差进行建模并利用自相关函数和最小均方(Least Mean Square, LMS)迭代算法进行了失配误差的估计。

目前只有少量的文章对TIADC带有记忆效应的非线性失配误差的估计和校正方法进行研究。文献[19]提出了联合盲校正算法对双通道TIADC的带有记忆效应的非线性失配误差进行校正，使用归一化最小均方(normalized-LMS)算法对非线性失配误差进行估计和补偿，但是该方法只适用于两通道非线性失配误差的校正，难以扩展到多通道的情况；文献[20]提出了多相非线性均衡器(polyphase NonLinear EQualizer, pNLEQ)，可以同时对线性失配误差和高阶非线性失配误差进行校正，但是因为校正过程涉及复杂的复数运算，会消耗大量的硬件资源，所以不便在实际的硬件结构中实现。

本文针对M通道的TIADC带有记忆效应的非线性失配误差提出了一种基于子通道重构结构的盲校正方法。相比于BWE和哈达玛变换的方法：首先，不仅能对静态非线性失配误差进行校正，还能对带有记忆效应的非线性失配误差进行校正；其次，不需要产生正弦调制序列，有更少的硬件资源消耗；最后，LMS算法模块以及误差重构中乘法器模块的工作频率仅为TIADC总采样频率的1/M，降低了系统功耗。

2 系统建模

理想的TIADC结构如图1所示，本文假设只存在带有记忆效应的非线性失配误差，偏置失配、增益失配以及时间失配误差均已对其进行补偿。

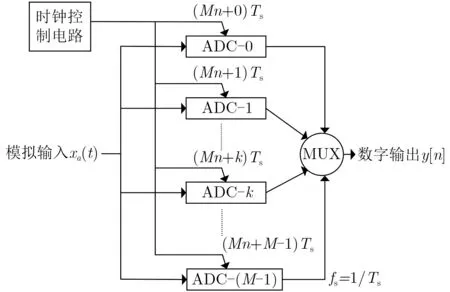
图1 TIADC结构示意图

2.1 带有记忆效应的非线性失配误差的子ADC的离散模型

本文考虑一个带限的模拟输入信号xa(t)，其最高频率为fmax。xa(t)的模拟频谱(傅里叶变换)表示为Xa(jΩ)，其中Ω=2 πf表示模拟角频率(rad/s)，f表示模拟频率(Hz)。

采样周期为Ts理想ADC的离散时间输出信号表示为

xd[n]的数字频谱离散时间傅里叶变换(Discrete-Time Fourier Transform, DTFT)表示为Xd(ejω)，其中ω表示采样率为fs下的数字角频率(弧度/采样周期，rad/sample)，关系为

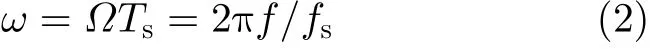
因此，模拟频谱和数字频谱之间的关系可表示为[21]

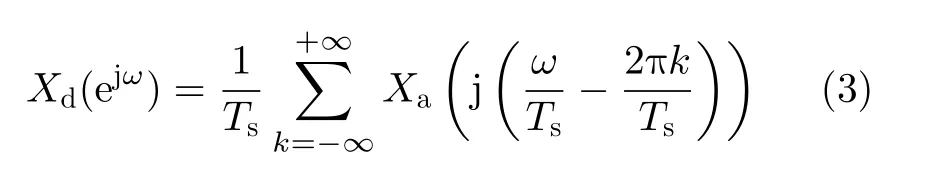
图2是带有记忆效应的非线性失配误差的子ADC的离散模型，模拟输入信号xa(t)首先经过采样得到了离散信号xd[n]，然后经过P 阶的离散时间Volterra级数(Discrete Time Volterra Series, DTVS)后得到了输出信号xv[n]，因为本文仅考虑非线性失配误差，所以2≤p≤P，DTVS的表达式为

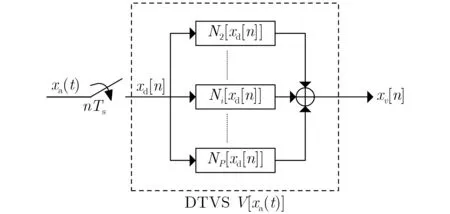
图2 带有记忆效应的非线性失配误差的子ADC的离散模型

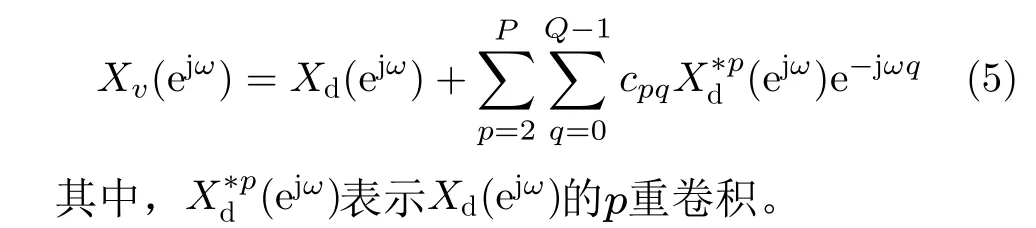
2.2 带有记忆效应的非线性失配误差的TIADC的离散模型

对于一个M通道的TIADC，每个子ADC都具有不同的非线性误差，整个系统的离散等效模型如图3所示。为了方便后续表示，2.1节中的模拟输入信号xa(t)以及第m通道采样后的值分别用x(t)以及xm[nM]表示。此外，不同于2.1节的单通道ADC，本节以及之后的内容，TIADC的采样率和采样周期为fs以及Ts，而每个子ADC的采样周期为TIADC的M倍，即MTs。

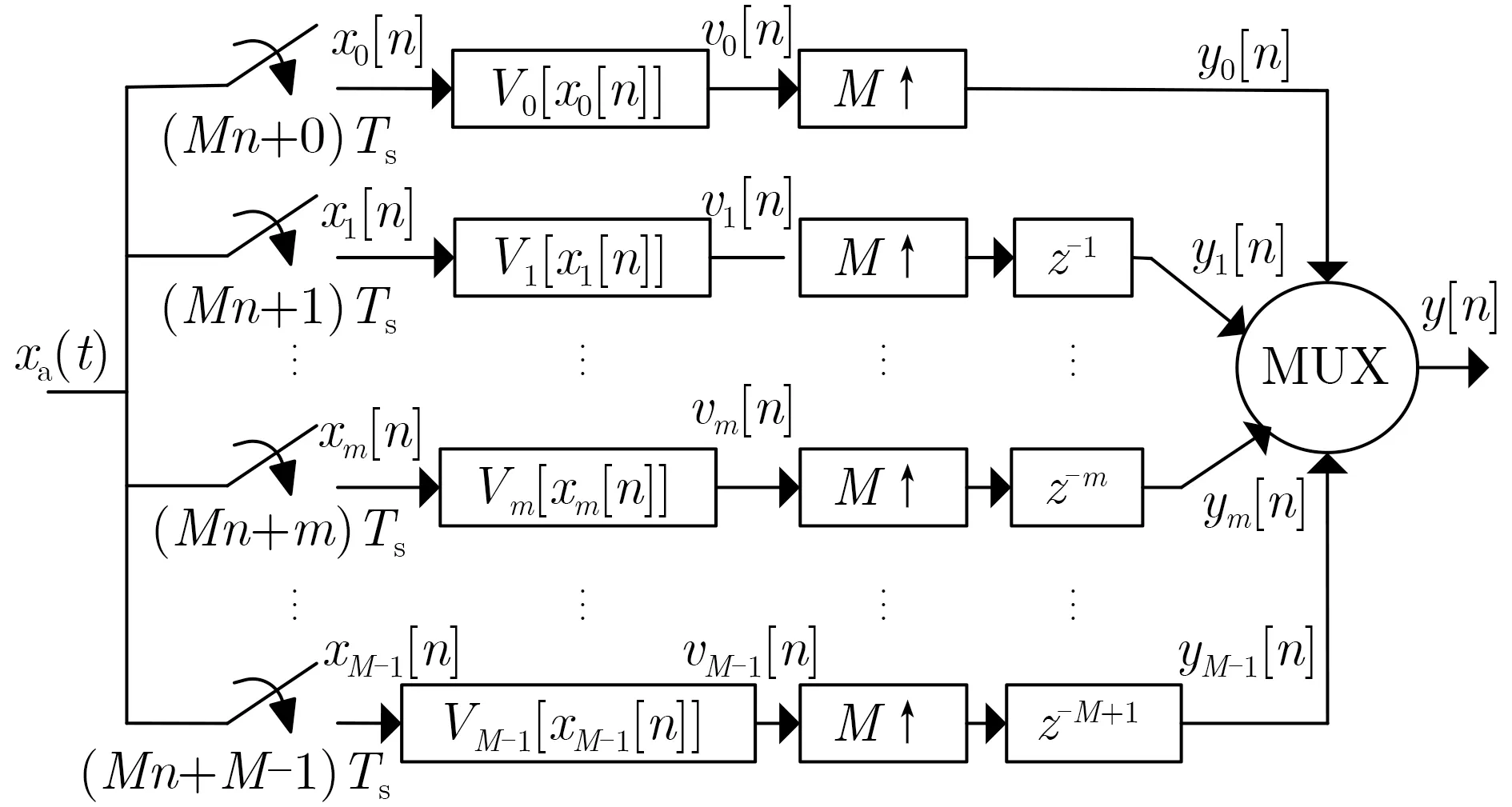
图3 带有记忆效应的非线性失配误差的TIADC的离散模型

由2.1节中的理论可知，第m个子ADC的降采样序列xm[v]可以表示为

其傅里叶变换表示为

cm,p,q表示第m个子ADC的p阶非线性项记忆长度为q时的误差系数。

ym[v]经过升采样并相加之后得到了TIADC的输出y[n]，其表达式为

3 校正方法

基于图3中的TIADC等效模型，本节提出了一种针对M通道中带有记忆效应的非线性失配误差的自适应盲校正方法。校正方法的基本原理是利用估计的非线性误差系数和子通道重构结构(Sub-Channel Reconstruction, SCR)重构误差信号，然后从TIADC的输出中减去误差信号，采用了滤波降采样最小二乘(Filtered-Down-sampled Least Mean Square, FDLMS)算法在输入无关频带(Input Free Band, IFB)中得到误差信号以此来估计非线性误差系数。

3.1 校正结构

误差信号e[n]可以由输入信号x[n]进行完美重构，但是实际情况中，输入信号是未知的，可以用y[n]来近似x[n]进行重构[17]。重构信号可以表示为

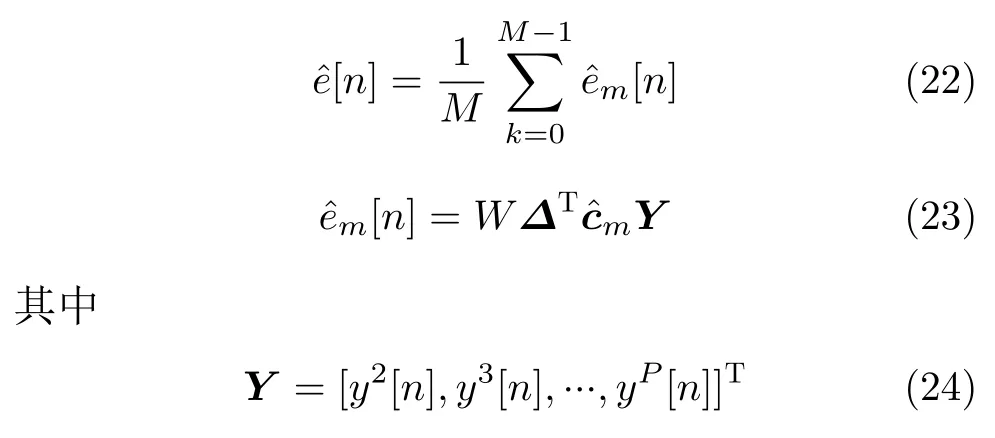
cˆm表示误差估计矩阵。

图4展示了M通道TIADC的校正结构，TIADC的输出y[n]经过M倍降采样率的降采样模块，数据的频率降到了TIADC总采样率的1/M，也就是每个子ADC的采样率fs/M。后续模块的工作频率也均为fs/M。降采样模块子通道输出ym[v]通过子通道误差重构(Sub-Channel Reconstruction, SCR)模块后，再经过升采样模块以及一个单位的延迟得到了重构后的误差信号eˆ[n]。利用ym[v]进行乘方操作依次得到2阶项ym2[v]到最高阶P阶项ymP[v]，然后分别乘以对应的系数cm,2,0～cm,P,0，再累加得到了一个基本误差重构单元(Basic Error Reconstruction Unit, BERU)，利用ym[v]得到Q-1个延时分量ym[v-1]～ym[v-Q+1]，这Q-1个延时分量再经过Q-1个基本误差重构单元，最后将Q个基本误差重构单元的输出合并得到重构后的信号yRS_m[v]，其公式为

图4 M通道TIADC带有记忆效应的非线性误差校正原理结构图

3.2 估计结构和整体框架

为了估计系数矩阵cm的值，考虑一个带限输入信号，带宽范围为[0, βπ]，其中0<β<1。若TIADC内不存在任何误差，那么在TIADC的输出频谱仅在[0,βπ]内有信号能量，当非线性误差存在时，在[βπ,π]频带范围内将会产生误差能量，但是没有输入信号的能量，这个部分称为输入无关频带(Input Free Band, IFB)或者失配频带(Mismatch Band)。图5给出了含有2阶非线性误差的四通道TIADC的IFB示意图，其中X(jΩ)和E(jΩ)分别表示x[n]和e[n]的连续时间傅里叶变换。因此在[βπ,π]范围内的这部分能量可以通过一个高通滤波器滤出并结合FDLMS算法对误差系数矩阵cm进行估计。误差信号e[n]经过高通滤波器f[n]滤波后的误差滤波信号ε[n]表示为

图5 含有2阶非线性误差的四通道TIADC输入无关频带示意图[7]

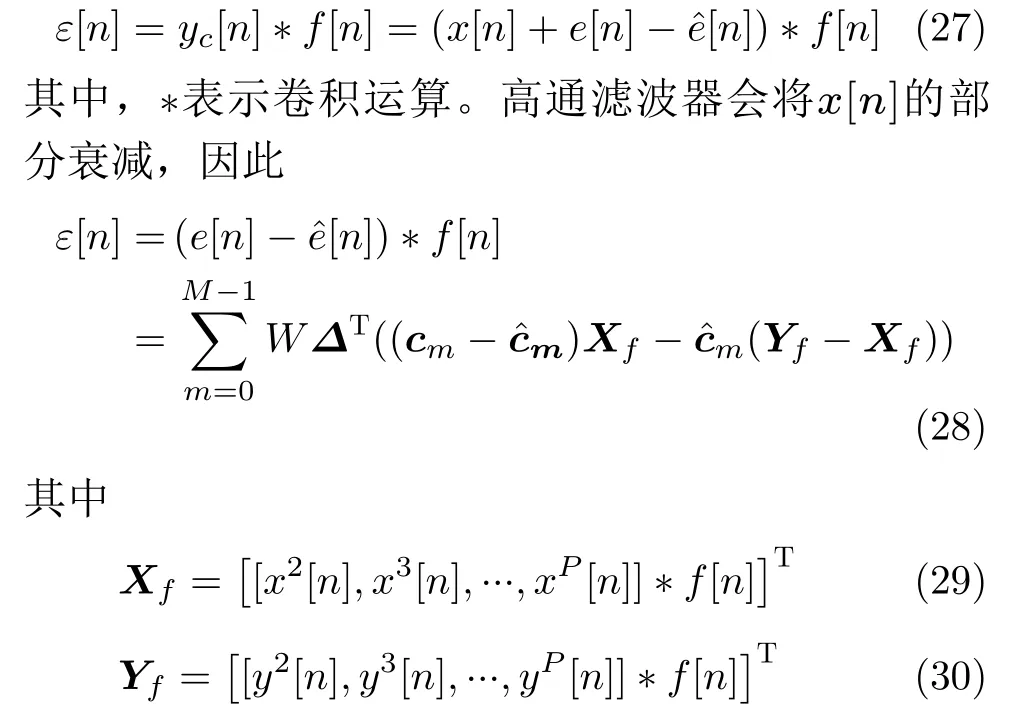
表示信号向量X和Y经过高通滤波器之后的部分。图6为基于FDLMS迭代算法的M通道TIADC的非线性误差自适应盲校正的结构示意图，D代表高通滤波器f[n]的延迟，ε[n]经过另外一个降采样模块得到εm[v],m=0, 1, 2, ··· , M-1。LMS为最小均方算法模块，估计误差系数矩阵cˆm中元素cˆm(q,p-2)=cˆm,p,q基于FDLMS迭代算法的迭代公式为

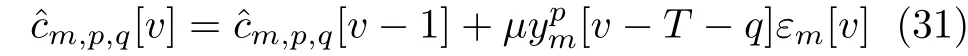
其中，µ为迭代步长，T=-(M+D)/M。迭代式(31)通过不断迭代减小ε[n]的值，当式(31)收敛时，ε[n]的值被减到最小，从而估计出系数cˆm,p,q的值，进而得到估计的系数矩阵cˆm。 图6中采用了向量表达方式使得图示更简洁，其中

图6 基于FDLMS算法的M通道自适应盲校正算法结构示意图

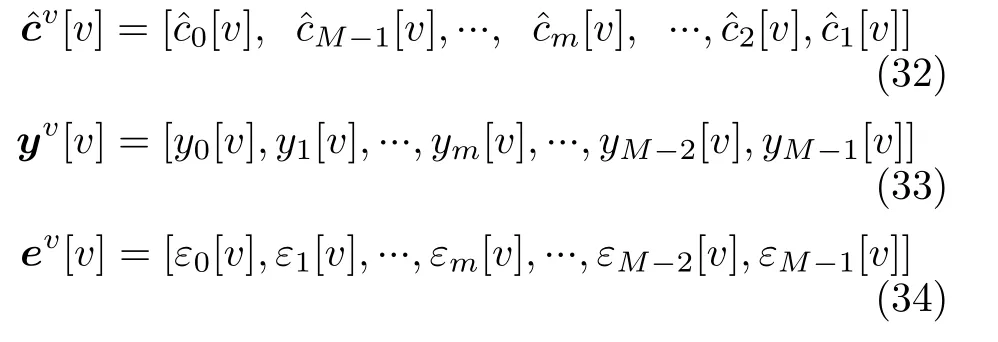
4 仿真结与实验

本节展示了所提出校正结构的仿真结果。利用MATLAB Simulink建立了四通道、16 bit的TIADC模型，高通滤波器利用FADTOOL工具进行设计，阶数为40阶，通带左侧归一化频率设置为0.8π。迭代步长µ设置为0.001，估计系数矩阵cˆm(m=0, 1, ··· , M-1)初始设为零矩阵，非线性最高阶设置为3，记忆长度为2，系数矩阵c设置为

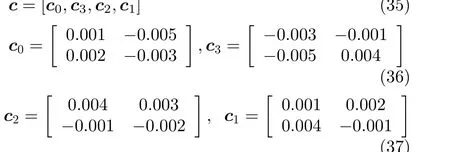
4.1 多频点实验

本实验选取了如下输入信号

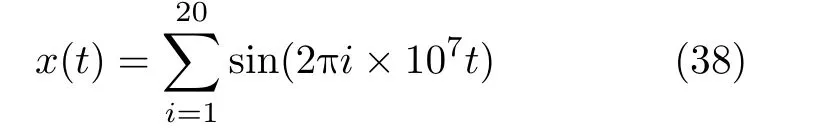
由DC到0.79π(归一化频率)均匀分布的正弦信号。图7比较了校正前后的频谱。从结果可以看出，本文所提出的校正方法有效地提高了TIADC系统的无杂散动态范围(Spurious Free Dynamic Range,SFDR)。校正之前由于非线性失配误差，TIADC的SFDR只有51.1083 dB，校正之后，TIADC的SFDR增加到了92.3539 dB。图8给出了每个通道分支对应的误差收敛曲线，其中黑色虚线表示真实值。

图7 多频点输入信号校正效果示意图

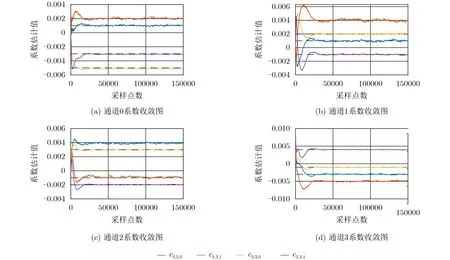
图8 多频点输入信号情况下误差收敛曲线

4.2 白噪声实验

本实验选取了一个低通信号，仍然使用4.1节中的四通道TIADC。一个均值为0，方差为1的高斯白噪声信号经过一个截止频率为0.78π的低通滤波器得到所需的低通信号。为了量化在通带中的校正效果，本文计算了误差向量幅度(Error Vector Magnitude, EVM)，其公式为[16]

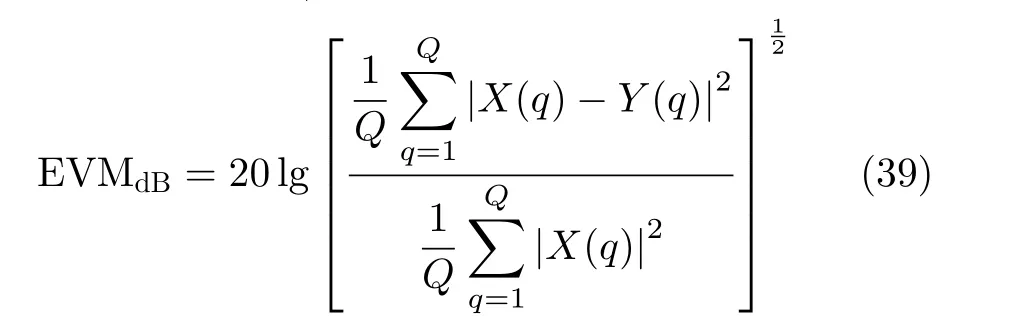
其中，X(q)表示期望信号的频谱，而Y(q)则表示校正信号的频谱。Q是FFT的总点数(图9中采用了点数为3.2×104的FFT)。图9是校正前后的频谱对比，可以看到，TIADC系统在输入无关带中的最大失真由-49.74 dB降低到了-89.85 dB，图10给出了4个子通道所对应的误差收敛曲线，黑色虚线代表系数的真实值。TIADC校正前后的EVMdB分别为-47.77 dB和-88.11 dB。

图9 低通白噪声输入信号校正效果示意图

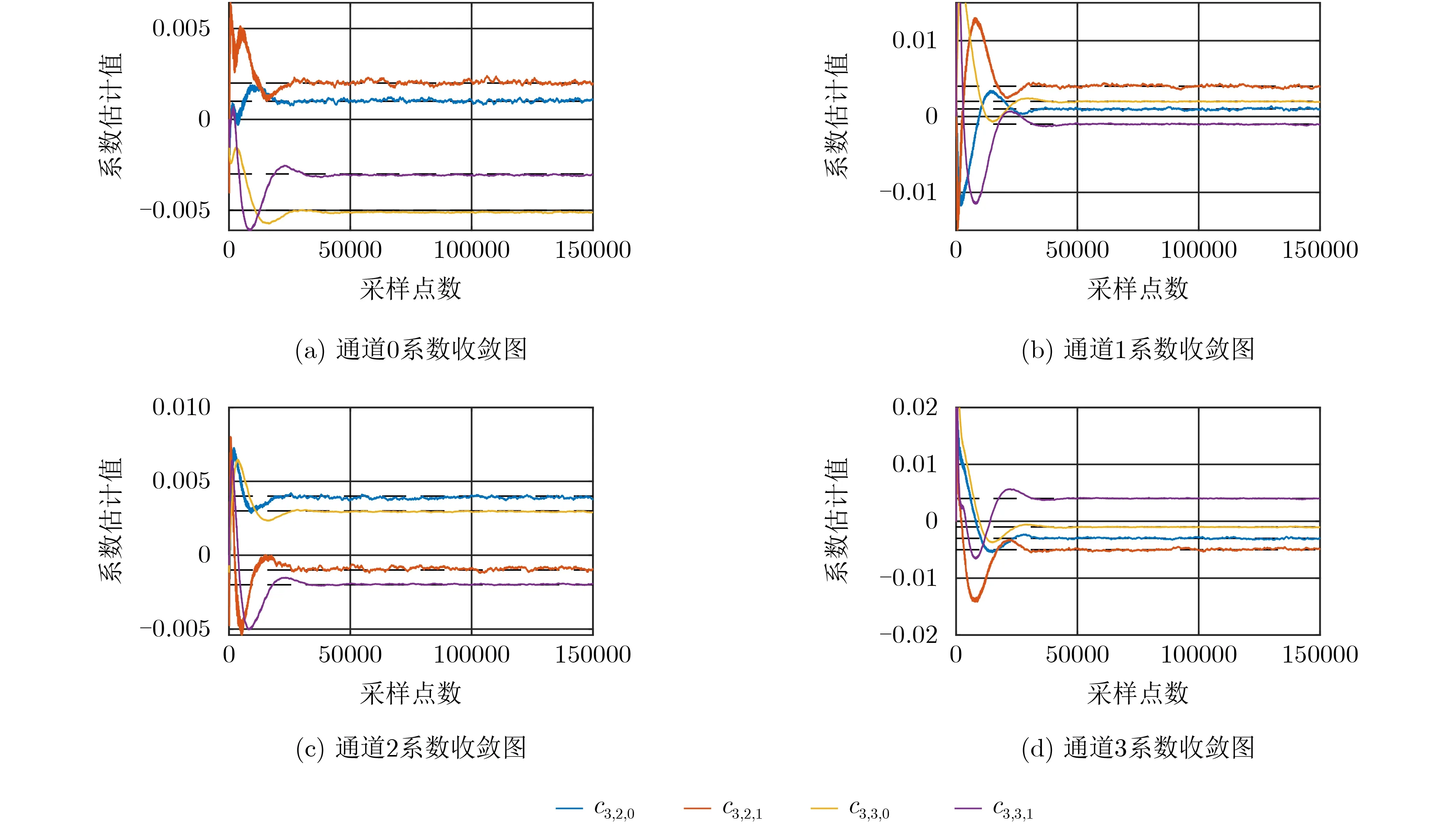
图10 低通白噪声输入信号情况下误差收敛曲线

4.3 计算复杂度

本节分析了所提出方法的计算复杂度。本方法对比其他论文主要的优势在于对硬件资源消耗更少，避免了正弦调制信号。此外，本文的带有记忆效应的校正结构也适用于静态非线性失配误差校正，当记忆长度为1的时候，所提出的结构即等效于静态非线性模型。从图6可以看到，一个BERU里面的乘法器数目为2(P-1)，因此每一个降采样后的SCR模块包含乘法器数目为2(P-1)Q，总的乘法器数目为2M(P-1)Q，但是这些乘法器工作频率均为Fs/M，因此就等效于在Fs的工作频率下使用了2(P-1)Q个乘法器[16]，加上高通滤波器的乘法器数目Nf/2+1，本文校正算法每个采样周期使用的乘法器数目为2(P-1)Q+Nf/2+1。表1给出了本文和其他方法的对比。对比文献[16]和文献[17]，在只考虑静态非线性的情况下，本文采用方法的乘法器较少，且不需要调制器，避免了生成正弦序列的复杂电路。

表1 计算复杂度的对比

图11展示了3种方法所消耗的乘法器数量以及乘法器数目的比率。高通滤波器的阶数为44，因此系数对称的有限冲激响应(Finite Impulse Response,FIR)滤波器乘法器数目为22，可以看到，随着通道数目M以及非线性最高阶数P的增加，BWE方法[16]以及哈达玛矩阵调制方法[17]的计算复杂度不断增加，而本文的方法仅随着非线性误差最高阶P以及记忆长度Q增长，和通道数目M无关。在M=16,P=7, Q=2时3种方法消耗乘法器数目分别(BWE、哈达玛、本文)为227, 125和47，消耗乘法器比率分别为6.31和3.57。本文所提结构硬件消耗远小于另外两种方法。其中比率公式为

图11 计算复杂度对比

5 结束语

本文介绍了一种自适应盲校正方法来校正M通道TIADC中带有记忆效应的非线性失配误差。通过子通道重构结构(SCR)重构非线性引起的误差信号，并通过FDLMS算法估计了各通道的非线性失配误差系数。本文所提出的方法首先不仅能校正静态非线性失配误差，也能校正带有记忆效应的非线性失配误差，其次避免了调制器的使用，与基于正弦序列和哈达玛变换的方法相比，硬件资源和功耗大量减少。