一种适用于椒盐-高斯干扰信号的自适应滤波改进算法*
高东生,廖泓舟,王 侃,代 翔
(1.中国人民解放军31434部队,沈阳 110086;2.中国西南电子技术研究所,成都 610036)
0 引 言
现今,通过通信网络传送、存储、检索或广播图像与文字等视觉信息的业务层出不穷,多种多样的图像信号接连出现,但是由于拍摄装备本身的特点和通信过程中的光-电转换机制,图像通信一般都掺杂着噪声,导致了图像信号质量的下降[1]。当干扰信号噪声污染严重时,一些图像信号甚至会出现失真,损失了信号的本质特征和价值[2-3]。因此,在使用图像信号之前需要先进行预处理,最大程度地保留信号的本质信息。图像通信在平滑、采样、量化、转化的物理处理过程中,原始信号更多时候会被引入椒盐-高斯干扰信号噪声,而不是单一的椒盐噪声或高斯噪声。均值滤波和中值滤波分别被认为是滤除高斯噪声和椒盐噪声最简单和实用的方法之一[4-5],然而,当噪声是污染严重的混合噪声时,单一干扰信号噪声之间的交叉影响会导致单一的滤波方法不能有效去除混合噪声,导致滤波失败[6-7]。
一直以来,国内外学者在图像通信滤波上都有着深入的研究。文献[8]研究了多种中值滤波的变体,在椒盐噪声上取得了优异的效果,但是各种变体对椒盐-高斯干扰信号噪声滤波效果不理想。文献[9]提出了自适应加权均值滤波算法,对高斯噪声产生了明显的抑制作用,但是针对严重的椒盐-高斯噪声,该方法仍然效果不佳。文献[10]最早提出了改进的均值滤波算法,即MTM(Modified Trimmed Mean)算法,首次将中值滤波和均值滤波进行了联合,相比传统单一滤波方法,在混合噪声滤波效果上有着本质的改观,但是该算法对阈值的设定十分敏感。针对文献[10]阈值敏感的问题,文献[11]提出了基于MTM的自适应阈值混合算法,即IMF(Improved Median Filtering)算法,克服了MTM算法的弊端,但是滤波效果受不同噪声之间耦合关系和噪声密度大小影响较大。因此,文献[12]在文献[11]的基础上改善了自适应均值滤波算法,提出平均阈值概念,称为IAAF(Improved Adaptive Average Filtering)算法,通过设定平均阈值较好地降低了交叉噪声对输出的影响。IAAF算法相比MTM和IMF算法在阈值自适应上有很大的创新,实用性强,存在许多IAAF思想衍生而来的新算法和应用,如文献[13]基于IAAF思想,增加了噪声点预处理环节,滤波效果得到有效提升;文献[14]则借鉴IAAF思想进行隧道混合噪声滤波,既降低了混合噪声,又保护了信号边缘信息。
本文首先对MTM、IMF、IAAF等演进算法进行分析,针对算法存在的不足进行改进,并通过实验进行了算法对比验证。
1 MTM及其演进算法分析
MTM算法是最早用于解决椒盐-高斯干扰信号的联合滤波方法,其主要思想是:针对一幅图像,在处理图像中第x(i,j)个点时,首先以当前点为中心确定滤波窗口,并对滤波窗口进行中值滤波,获得当前滤波窗口的中值,然后以当前滤波窗口的中值为中心,以一定灰度步长确定均值滤波区间,再进行指定区间内的像素均值滤波,并获得最终滤波输出。该方法首次将两种方法进行了联合,可表示如下:
(1)
式中:y表示中值-均值联合滤波输出结果,Wij表示滤波窗口,median表示滤波窗口的中值,step表示灰度步长值。
由式(1)可知,滤波窗口大小W和灰度步长值step需要人为确定,MTM算法存在阈值选择困难的问题。
针对MTM算法阈值选择存在的不足,IMF算法被提出,其主要思想是:针对一幅图像,在处理图像中第x(i,j)个点时,首先以当前点确定一个滤波窗口W,并计算出滤波窗口中的中值mi,j,然后计算滤波窗口内各像素点与中值的方差d(m,n),根据方差计算各像素点的归一化加权系数Avei(m,n),最终通过加权系数对窗口内像素进行加权平均,获得最终滤波输出。该方法可表示如下:
d(m,n)=(X(m,n)-mi,j)2,
(2)
Ii(m,n)=1/(1+di(m,n)),
(3)
sum=I1(m,n)+I2(m,n)+...+IM×M(m,n),
(4)
Avei(m,n)=Ii(m,n)/sum。
(5)
式中:d(m,n)是滤波窗口中每个像素与中值的方差;Ii(m,n)是为均值滤波加权系数;Avei(m,n)是均值滤波归一化加权系数,其中i=1,2,…,M×M。
IMF算法成功解决了MTM算法阈值选择困难的问题,但通过式(2)~(7)可以发现,IMF只考虑了滤波窗口中的中值与相邻像素点的距离,而没有考虑相邻像素本身性质的问题,如果与中值大小相近的像素点本身是噪声点,那么它与中值的方差会很小,这就会导致噪声点的加权权重很高,反而扩大了干扰信号噪声点对滤波输出的影响。
针对IMF算法在相邻噪声点像素对均值加权滤波输出的影响问题,IAAF被提出,其基本思想是,基于IMF算法求取滤波窗口内每点像素与中值的方差Ei,然后求取所有方差的均值T(称其为阈值),若Ei大于阈值T,则权值由Ei决定,反之由T决定。阈值计算公式如下:
(6)
式中:Tmn为滤波窗口内各像素与中值方差的均值。
IAAF算法直接避免了噪声点对滤波输出的影响,但是该算法存在两点不足:一是忽略了滤波窗口的中值本身是噪声点的情况,尤其在图像污染严重时,中值滤波选择的结果可能仍是噪声,这种情况会使得T失去效能;二是以方差均值T作为阈值,在降低相似噪声点影响的同时也直接降低了正常相似像素点对输出结果的正向影响。
2 改进的快速自适应混合滤波(IFAHF)
2.1 算法思路与步骤
本文针对IAAF算法存在的不足进行了改进,提出了改进的快速自适应混合滤波(Improved Fast Adaptive Hybrid Filtering,IFAHF)算法,主要思想是:首选获取图像f,尺寸为X×Y(X为图像的长度,Y为图像的宽度),同时在图像上任取一像素点x(i,j)并确定初始滤波窗口W,根据经典图像通信滤波经验,初始窗口尺寸为3×3,然后针对当前滤波窗口W中的元素点通过自适应中值滤波方法进行噪声点辨识,先分辨出当前滤波窗口W中存在的噪声点,同时根据相同噪声密度下滤波窗口越大中值为噪声点的可能性越小的原则,将窗口大小的平方即W×W作为当前窗口下滤波输出的加权系数,在对噪声辨识的过程中通过逐级扩大的方式自适应扩展滤波窗口W的尺寸(本文借鉴贪婪思想,采取长和宽分别加1的逐级扩大方式,直到满足滤波要求或规定阈值的窗口尺寸,则不再进行扩展),并在自适应扩展过程中,计算当前窗口下滤波输出,最后对所有扩展滤波窗口获取的滤波输出进行加权平均,获得最终滤波输出。算法流程如图1所示。
本文改进算法步骤如下:
设受椒盐-高斯干扰信号污染的图像为f,滤波输出图像为F,尺寸为X×Y(X为长,Y为宽),滤波窗口为W,整个滤波过程采取从左至右、从上到小的顺序。
(1)干扰信号噪声点辨识
中值滤波可以有效抑制椒盐噪声,但是在图像受污染严重时,中值滤波效果会受到很大影响,滤波后的中值仍可能为噪声点,若中值是噪声点,后续加权均值滤波将会受到直接的影响,甚至会扩大噪声点的影响,因此首选需要对噪声点进行辨识。噪声点辨识的主要步骤是:对于图像中任意一个像素点x(i,j)(i是横坐标,j是纵坐标),滤波窗口以x(i,j)为中心,计算滤波窗口中的像素点的最大值Smax、最小值Smin和中值Smed。如果Smed满足
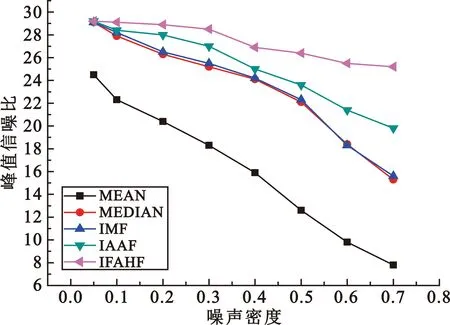
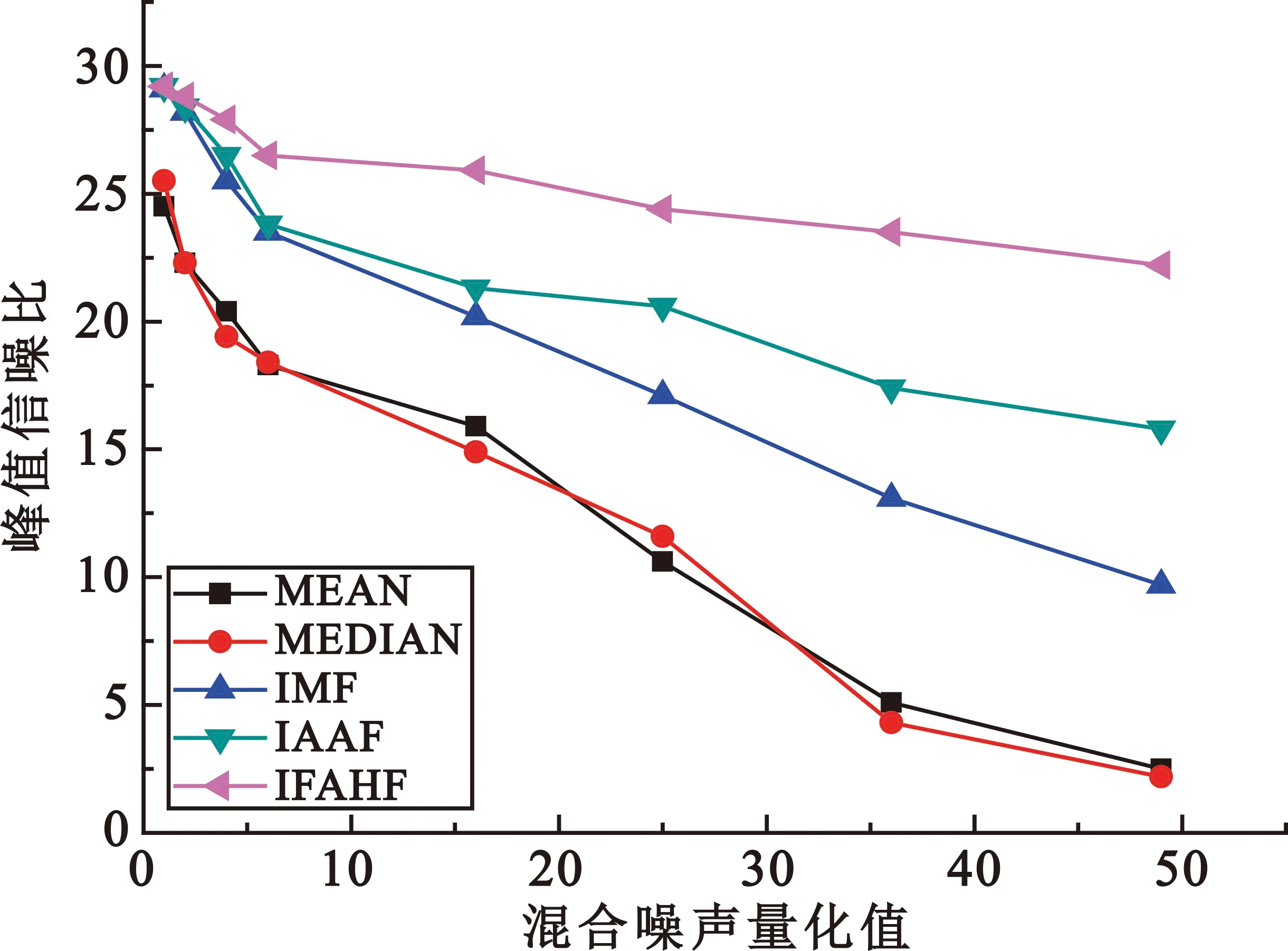
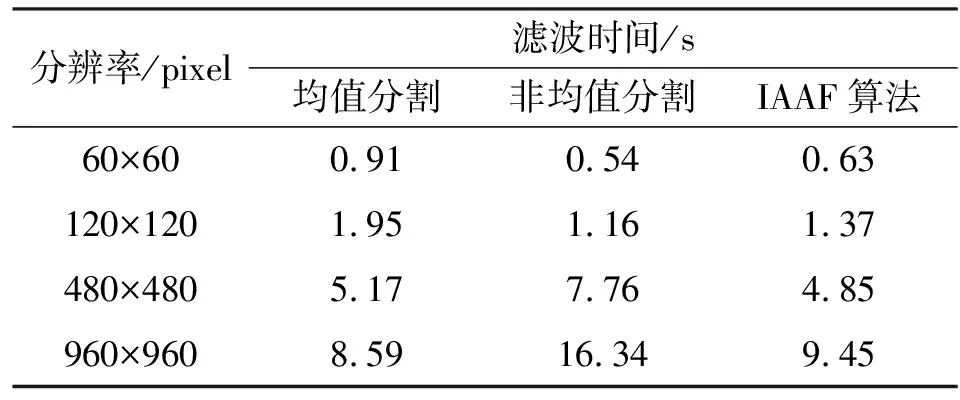
Smin (7) 则当前滤波窗口中获得的中值不是噪声点,当前窗口满足要求且可用;相反,如果滤波窗口不可用,则按w+1的原则(w是窗口尺寸)进行窗口自适应扩展,直到满足式(7)或 w≤T。 (8) 式中:w是窗口尺寸;T是滤波窗口最大尺寸,T=min(X,Y)。 (2)计算各滤波窗口归一化系数及中间输出 干扰信号噪声点辨识是一个动态的过程,噪声污染严重时,一次辨识可能是无效的,需要不断扩展窗口进行多次辨识,直至中值输出为非噪声点。因此,噪声点辨识是一个窗口不断自适应扩展的过程,每一次窗口扩展都代表着当前滤波窗口下当前点x(i,j)附近噪声点的密集程度,扩展次数越多,代表当前点x(i,j)附近噪声越密集,中值滤波输出为中值的概率越小。本文将中值获取可能性即中值获取概率量化为窗口大小的平方数(窗口越大,中值获取概率越大,当前窗口下加权均值滤波效果好的概率也越大),从而量化不同窗口下均值滤波效果,最后通过多层级滤波窗口下滤波效果的加权平均获得最终的均值滤波效果。因此,首先需要进行不同窗口下的滤波效果量化,即计算各滤波窗口归一化系数与当前滤波窗口下的中间输出。 噪声辨识窗口自适应扩展过程中,计算各滤波窗口归一化加权系数: (9) 式中:kw(i,j)表示当前窗口(w×w)的归一化加权系数,窗口越大,归一化加权系数越大。 同时,计算当前点x(i,j)在各滤波窗口下的中间输出值: (10) (11) 式中:mw(i,j)表示点x(i,j)在当前窗口下(w×w)的中值。 (3)计算滤波输出 经过噪声辨识及窗口自适应扩展,获取各滤波窗口的归一化系数和多层级滤波窗口下的滤波效果量化值,即滤波中间输出tw(i,j);然后对量化的滤波效果进行加权平均,计算得到最终的中值-均值联合滤波输出。改进算法滤波输出可表示为 (12) 式中:F(i,j)表示点x(i,j)的滤波输出;w表示滤波窗口尺寸,w=1,2,3,…,T,T=min(X,Y),X、Y分别代表图像的长与宽。 由式(12)可知,本文改进算法计算滤波输出分为两个部分,一是计算kw(i,j),另一个是计算tw(i,j),而两者皆通过噪声点辨识的窗口自适应过程进行计算,无需人为确定参数,这也是本文改进算法的自适应体现。 本文算法通过量化多层级窗口滤波效果,并加权平均多层滤波效果获取最终的滤波输出,既考虑了IAAF算法中值本身是噪声点的问题,也避免了方差阈值对正常像素点的滤波抑制作用。但是,本文算法通过噪声点辨识增加了窗口滤波次数,在一定程度上增加了计算量,其中主要表现在滤波窗口扩展过程中寻找中值的次数增加。为了易于实用,提高滤波实时性,本文同时提出了均值分割加速的方法,加速中值滤波速度,提高滤波速度,具体流程如图2所示。 图2 均值分割流程图 均值分割的基本思路是将二维数组转换成一维数组,然后计算一维数组均值,并以均值为基础值将数组元素进行分割,小于等于均值的元素分割到均值左侧,大于均值的元素分割到均值右侧,并记录左右两侧元素个数,如N左和N右,通过如下关系进行下一次分割判: N左≥N/2 。 (13) 式中:N是元素总个数。 若式(13)满足则进行下一次分割直到满足如下关系: N左 (14) 满足式(14)则分割结束。 若式(13)不满足,则进行N右判断,判断原则与N左一致。 本文通过均值分割方法和部分排序的思想改进中值获取过程,步骤主要如下: 首先,判断均值分割是左侧分割还是右侧分割,如果是左侧分割,则保存最后一次分割过程中的N左,并按从小到大的顺序进行排序,因此,过程中无需完全排序,最终排序次数满足如下关系: w=N/2-n。 (15) 式中:n是最后一次分割过程中的N左。 相反,如果是右侧分割,则保存最后一次分割过程中的N右,并按照从大到小的顺序进行排序,最终排序次数满足如下关系: w=N/2-m。 (16) 式中:m是最后一次分割过程中的N右。 通过以上部分排序获得的元素即是滤波窗口的中值。 本文首先在基准图像——Lena图像上进行算法测试,与传统均值、中值等单一算法和IMF、IAAF等演进算法进行对比分析,并尝试在不同环境下进行测试,算法测试效果通过主观和客观两种方式进行科学综合评价。算法验证的主要软硬件环境为2.6 GHz双核CPU,内存4 GB,NVIDIA GT650M 2 GB独立显卡,Window8操作系统与Matlab 2014b处理软件。 Lena图像由于各个频段的能量都很丰富(既有低频信号,也有高频信号),很适合验证各种算法,因此是新算法测试的基准图像之一。噪声分为椒盐噪声和高斯噪声,其中椒盐噪声通过噪声密度进行量化,计算公式为 (17) 高斯噪声通过高斯分布进行量化,具体分布可表示为 (18) 式中:μ和σ分别表示高斯分布的期望和方差。 本文采用分辨率为512 pixel×512 pixel的Lena灰度图作为测试图像,干扰信号噪声从低噪声向高噪声逐渐转变,椒盐噪声密度从0.05(低噪声)增加到0.7(高噪声),高斯噪声均值设置为0(便于统一变量),方差从10(低噪声)增加到70(高噪声),采用客观指标峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)进行滤波效果定量比较与评价。PSNR可以通过如下公式表示: (19) (20) 式中:I和K分别为大小为m×n原始图像和噪声图像。 实验结果如图3所示。通过图3(a)可知,本文改进算法PSNR值在多种椒盐噪声下表现最好,单一均值滤波效果最差。图3(b)表明本文算法在多种高斯噪声下效果最优,单一中值滤波效果最差,从客观上来看本文改进算法具有更好的混合滤波效果。通过图3(c)可以发现,在高混合噪声的情况下,PSNR值相差值较大,本文改进算法滤波效果比较明显。图片受椒盐-高斯干扰信号噪声污染程度从主观上有轻微与重度两个视觉层次,客观上则体现为噪声密度大小。目前图像通信领域还没有一个统一客观的界定来规范区分低噪声与高噪声之间的范畴[15-16],因此本文设定椒盐噪声密度大于50%且高斯噪声大于50即为高混和干扰信号噪声,因为在这种程度的噪声污染下,信号质量从客观与主观上都表现很差。因此本文选取椒盐噪声密度=0.1、高斯均值=0、高斯方差=10的低混合噪声和椒盐噪声密度=0.6、高斯均值=0、高斯方差=60的高混合噪声两种不同含噪程度的图像进行可视化对比,结果分别如图4和图5所示。 (a)椒盐噪声PSNR曲线 (b)高斯噪声PSNR曲线 (c)混合噪声(椒盐密度×高斯方差)PSNR曲线图3 Lena图像测试结果 图4 低混合干扰信号噪声下各种算法滤波效果对比 图5 高混合干扰信号噪声下各种算法滤波效果对比 通过图4和图5的对比分析可知,在低混合干扰信号噪声情况下,单一的均值滤波、中值滤波和IMF滤波均能基本完成基本滤波任务,滤波效果主观上都是令人满意,同时IAAF和本文提出的IAAF下算法滤波效果相比前者滤波效果更优,但差距不是很明显,但是在高混合干扰信号噪声情况下IFAHF滤波效果相比较其他四种滤波方法则更为明显。实验证明本文算法在椒盐-高斯高混合干扰信号上处理效果更好,相比其他传统算法效果更为理想。 Lena基准图像测试结果表明本文提出的改进算法在椒盐-高斯高混合干扰信号噪声下相比其他均值、中值等单一滤波算法和IMF、IAAF等演进算法具有明显优势,本文同时尝试验证了在不同环境下改进算法的滤波效果,选择中等程度的椒盐-高斯干扰信号混合噪声,同时水下图像选择典型的蓝色背景,空中选择典型的蓝白背景。椒盐噪声密度=0.4,高斯均值=0,高斯方差=30,图像中不含其他类型噪声,验证结果如图6和图7所示。 通过对图6和图7的分析可知,在只考虑椒盐-高斯干扰信号混合噪声的情况下,本文改进算法在水上、水下环境中滤波效果均优于或者等同于其他四种滤波方法,表明该改进算法在抑制椒盐-高斯干扰信号混合噪声时受其他环境影响和图像色彩的约束比较小,处理算法在一定程度上可以迁移到其他环境下进行处理,具有一定的普适性。 通过图3~7的分析可知,本文改进算法在客观指标上表现较好,结合主观评价可以得出结论:本文提出改进算法能有效抑制椒盐-高斯干扰信号混合噪声,尤其是高混合噪声滤波效果明显,客观评价与主观评价是一致的。 滤波效果是很重要的一个方面,滤波时间即滤波实时性也是实际滤波一个非常重要且必须考虑的另一方面。在实际滤波过程中,大部分算法往往强调算法性能的优与劣而忽略了算法处理效果的实时性问题,从而导致算法仿真效果非常可观,但是实用性并不强的问题。因此,本文专门针对所提算法通过增加复杂度提升滤波效果而牺牲滤波实时性的问题,再次提出了均值分割算法进行弥补,通过两者的结合本文算法最终从性能和实时性上达到一个折中的效果。对本文算法中使用均值分割和不使用均值分割情况下滤波时间的大小,以及与IAAF算法时间比较,经过多次验证并取平均值,结果如表1所示。 表1 本文算法与IAAF算法滤波时间 通过表1可以得出两点结论:一是随着图像尺寸的增加,本文均值分割方法消耗时间较传统IAAF方法时间更低,增强了滤波实时性;二是随着图像尺寸的增加,本文提出的均值分割加速求取中值的方法相比不使用均值分割的情况,滤波时间显著缩短,同时,当图像尺寸比较小时,如分辨率为60 pixel×60 pixel、120 pixel×120 pixel时,本文滤波时间反而略高于非均值分割的情况。其原因主要是使用均值分割加速计算中值相比传统直接计算中值增加了分割操作和均值迭代等相关计算量,当图像尺寸比较小时,增加的这部分计算量所消耗的时间反而成为了最费时的部分,因此滤波时间反而更长。 由上述分析可以得出,本文提出的均值分割思想在大尺寸图像上更占优势,在小尺寸图像(如60 pixel×60 pixel)时,处理效率提升不明显,甚至会出现比传统方法处理时间更长的情况。 本文在椒盐-高斯干扰信号滤波演进算法的分析基础之上,针对多种演进算法存在的不足,提出了一种改进的快速自适应混合滤波算法,有效避免了高混合噪声点对滤波输出的影响,同时提出了均值分割方法,较好地提高了滤波实时性,增加了该算法的实用性。通过实验验证发现,本文改进算法能有效抑制椒盐-高斯干扰信号噪声,尤其是高混合噪声且在大尺寸图像滤波上更占时间优势。相关实验结果表明本文IFAHF算法相比IMF、IAAF等演进算法更为理想。此外,本文所提算法具有一定的普适性,后续可结合其他应用领域进行进一步验证。

2.2 均值分割加速获取中值思路与步骤
3 算法验证
3.1 基准Lena图像滤波效果比较

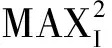



3.2 不同环境下滤波效果比较
3.3 本文算法滤波实时性效果
4 结 论

