复包络重采样超宽带目标信号模拟方法*

刘 奇，周良臣，周仕松

(成都信息工程大学 电子工程学院，成都 610225)

0 引 言

在测控通信、卫星导航[1]、深空探测[2]、协同定位[3]等很多应用场景中，目标信号模拟技术具有重要意义。近年来，相关研究主要集中在基于运动方程的多普勒频偏模拟方法上。根据目标的径向运动方程，目标运动时的距离、速度、加速度等信息体现在接收信号中的多普勒频偏上[4]，因此可以通过模拟多普勒频偏和多普勒频偏的变化率来模拟实际接收信号。这种方法的优点是从运动方程出发时间和速度严格相关，但增大系统模拟的距离，存储要求也会大大提高。文献[5]在此原理基础上提出了一种基于存储转发模式的动态模拟器，包括解调和不解调两种适应于不同数据速率场景的架构，能够缓解距离模拟与存储容量、读写速率要求之间的关系。为了能在保证远距离模拟[6]的基础上提高模拟精度，粗细时延组合控制采用两级存储方式进行动态模拟，粗时延控制读写间整数倍时钟周期的延迟，细时延控制读写时钟的相对相移。由于多普勒频偏精度直接影响了信号模拟精度，许多研究人员对系统中可实现的多普勒频偏处理方法进行了改进[7-9],但其方法模拟的目标信号都是窄带信号。用插值器做时域调整的方案首先在数字调制解调领域中被提出，文献[10]详细阐述了有关的基本方程、控制方法和信号处理特性。文献[11-12]对与时域调整息息相关的Farrow延时滤波器做了详细阐述。

当前模拟器普遍采用多普勒频偏模拟方法，在超宽带目标信号模拟中会有三个问题：难以准确模拟高动态目标信号的时变多普勒特性；忽略了信号传输过程中复包络的畸变；舍弃了目标信号的初始相位特性，多站协同探测情况下，可能导致目标在多个观测站间接收信号的相干特性遭到破坏。而如今超宽带系统应用越来越广泛，目标信号带宽也越来越大，必须找到一种更准确的超宽带目标信号模拟方法。

本文从时域调整和任意精度内插着手，提出了一种新型的基于复包络重采样算法的目标信号模拟方法，不仅保持了多普勒频偏模型的模拟优点，而且对超宽带目标信号中的时变多普勒特性、复包络变化、初始相位特性有准确的模拟效果，弥补了多普勒频偏模型的不足。

1 复包络重采样算法

1.1 接收信号模型

超宽带系统中，发射机的发射信号可表示为

s(t)=u(t)ej2πf0t。(1)

式中:f0为载波频率，u(t)为复包络信号。接收机上的接收信号可表示为

sr(t)=s[t-τ(t)]=u[t-τ(t)]ej2πf0[t-τ(t)]。

(2)

式中：τ(t)表示t时刻的传播延时。发射机和接收机间的距离R(t)可表示为t0时刻的初始距离R0和发射源瞬时速度v(t)的函数，即

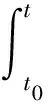
(3)

进一步，公式(2)中的延时τ(t)可表示为

(4)

式中：c表示电磁波的传播速度，τ0=R0/c是信号的初始时延。联合公式(2)和公式(4)，整理可得

(5)

式中：fd表示目标信号中的多普勒频率，

(6)

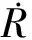
(7)

可以看出，接收机上的复包络信号在发射信号延时τ0的基础上还会产生畸变。当fd<0时，接收信号复包络会发生展宽现象；当fd>0时，接收信号复包络会发生压缩现象。传统多普勒频偏模型在模拟目标信号时，通常会忽略公式(5)中的初始相位项e-j2πf0τ0，复包络也会进一步简化，将接收信号近似表示为

sr(t)≈u(t-τ0)ej2πfd tej2πf0t。

(8)

多普勒频偏模型通过延时τ0和给目标信号附加多普勒调制的方式实现模拟。当信号满足窄带条件时，公式(8)的近似表示不会带来太大问题。但当信号不满足窄带条件时，如超宽带目标信号中包含有比较大的带宽，不同频率成分在接收信号中引起的多普勒频率是不一致的，引起整个接收信号频谱的变化。从时域来看，接收信号复包络的时间尺度会发生明显的伸缩变化。

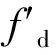
1.2 复包络重采样系统

复包络重采样技术用于模拟时变的距离时延τ(t)，利用公式(2)重新对发射信号的复包络进行采样作为模拟器的输出。当信号发射源为变速运动时，τ(t) 随时间变化而变化且几乎均不是采样周期Ts的整数倍。为了更直观地表述，本文直接讨论在数字域进行时延模拟，相应地均用τ(m)等离散时间变量函数表示τ(t)等时间函数。基于复包络重采样算法的目标信号模拟系统原理如图1所示。

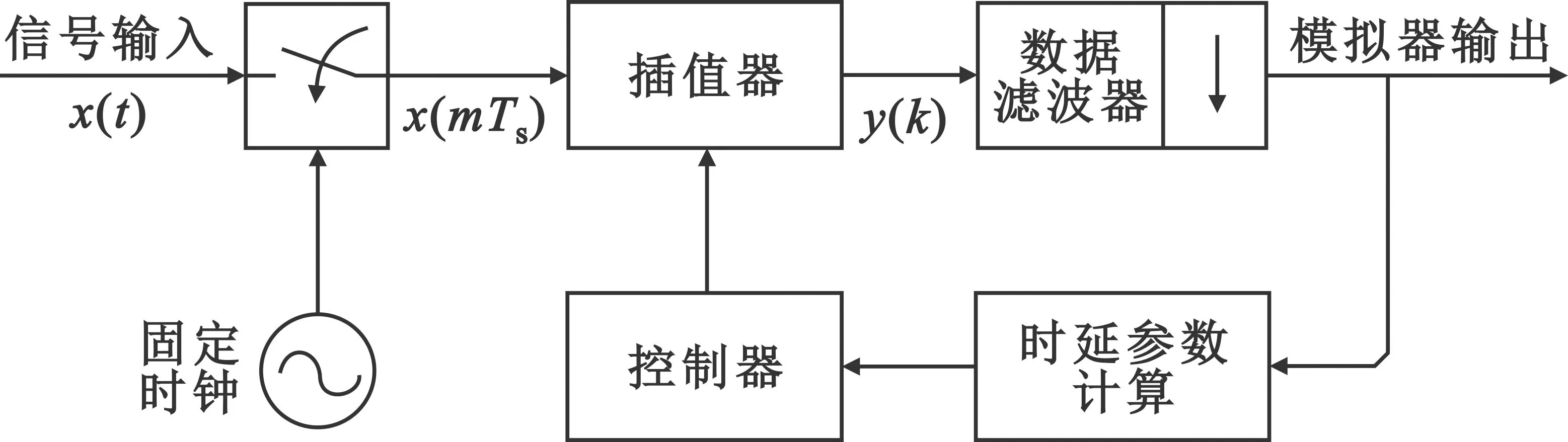
图1 复包络重采样信号模拟器系统框图

插值滤波器可以实现信号的时序调整[10]。时间连续信号x(t)以1/Ts速率无混淆采样，采样后信号用x(mTs)=x(m)表示。插值滤波器的数据输出时钟与输入时钟相同，则x(m)送入插值滤波器中，得到插值后输出y(k)=x[m-τ(k)]。插值器要能够调整时延τ(m)，得到期望时刻的重采样输出。插值器的基本方程可表示为

(9)

式中：hI(t)是一个假设的模拟插值滤波器的脉冲响应。在数字域中实现公式(9)，还需要做进一步转换。用i表示插值滤波器的系数索引，定义为

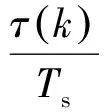
(10)

式中：⎣·」表示向下取整运算。将要调整的时间间隔分为基准位置mk和小数间隔μk，表达式如下：

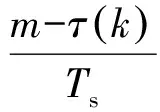
(11)

(12)

式(12)中：0≤μk<1。插值器的输入、输出数据的时间关系如图2所示。

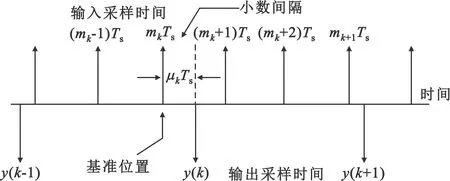
图2 插值滤波器输入/输出采样关系

公式(9)中的m=mk-i，且有τ(k)=(i+μk)Ts。插值滤波器的目的便是恢复出(mk+μk)Ts处的值，实现对输入信号的重采样。公式(9)可以表示为

y(k)=y[(mk+μk)Ts]=

(13)

式(13)便是复包络重采样算法中数字插值器的实现基础。插值滤波器通常使用有限脉冲响应(Finite Impulse Response,FIR)滤波器，则I1和I2为固定值，计算插值结果的滤波器有I=I1+I2-1个抽头。对于复包络重采样算法而言，μk是一个小数且在每次插值中都是变化的。

图1中，根据当前模拟器的输出以及要模拟的目标运动模型计算出发射至接收间的传播时延；控制器根据时延参数调整插值器中的mk、μk、滤波器系数等参数，实时更新插值器输出；数据滤波器进行抽取滤波，决定了模拟器的输出速率；环路控制实现了信号模拟的功能。

1.3 插值器实现方法

基于多项式的滤波器是一种常用的插值函数。多项式插值一般用Lagrange系数来表示，即由Lagrange系数公式构成脉冲响应hI(t)，是一个关于t(或者μk)的I-1阶多项式或分段多项式。选择I的大小要遵守两点：一是插值的样本集数量必须是偶数，即多项式的次数为奇数；二是只能进行在样本集的中心区间内的插值计算。

理论上要实现最优的插值效果，每次插值都要重新载入新的样本点和滤波器系数(hI(t)的采样)。实现插值滤波器时，一种方式是先将μk量化为L个均匀区间，与L个μk值相关的滤波器系数存储在内存中，计算插值时根据μk来寻址；另一种方式是动态计算系数并随样本点一同载入，无需存储。

Farrow结构是一种非常适合在硬件中实现信号插值的方法[11-12]。假设脉冲响应是以Ts分段、从i=I1到I2的分段多项式：

(14)

将公式(14)代入公式(13)中，可得插值器执行的计算为

(15)

式中：系数bl(i)可以是固定的或者可变的[13]。执行一次插值运算共需N·I个系数，I由脉冲响应的持续时间确定，N由滤波器的分段多项式确定。以三次插值为例，Farrow结构滤波器的硬件实现原理如图3所示。Farrow结构由N+1列横向FIR滤波器组成，每列有I个抽头。图3中每个抽头采用固定系数，表1是三次插值多项式根据Lagrange公式计算出的Farrow系数{bl(i)}。更广泛地来说，任何插值滤波器都能用Farrow结构实现。综上所述，Farrow结构滤波非常适合用于本文提出的目标信号模拟方案，实现目标信号复包络序列的重采样。

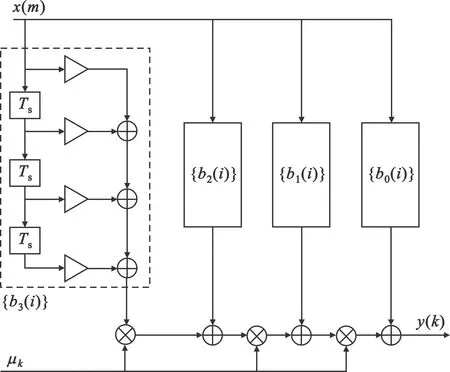
图3 三次插值的Farrow结构实现

表1 三次插值Farrow系数bl(i)

2 仿真验证

算法验证方案如图4所示，产生的距离参数和发射信号送入复包络重采样计算模块和频偏模型计算模块，生成两种目标模拟信号。假设目标为点目标，发射源与观测站之间做径向运动，选择正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)这种典型的超宽带信号进行模拟仿真。仿真采用基带带宽为528 MHz的OFDM信号，选取4 096个子载波，子载波间隔为128.906 25 kHz。信号采样率为2.112 GHz，对OFDM信号进行4倍采样，则一个OFDM符号中应包含16 384个采样数据。通信数据采用16QAM的调制方式加载到OFDM信号上，随机产生数据符号。载波频率f0为3.6 GHz。

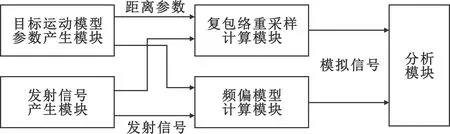
图4 算法验证方案框图

2.1 EVM分析

误差矢量幅度(Error Vector Magnitude，EVM)是信号链中常用的测试指标，可反应测量信号和参考信号之间的误差。利用公式(2)产生理想无误差的OFDM基准信号s1(t)，复包络重采样算法产生的OFDM目标模拟信号记为s2(t)，多普勒频偏模型产生的OFDM目标模拟信号记为s3(t)。衡量模拟信号和参考信号之间的EVM计算公式为

(16)

EVM即误差矢量的均方根值(Root Mean Square，RMS)和参考矢量的均方根值之间的比值，以百分比的形式表示，值越小则表示模拟效果越好。

第一种情况先排除速度变化的影响，目标运动模型先采用匀速模型，假设发射源以8.8 km/s的径向速度朝远离观测站的方向运动。采用两种方法产生目标模拟信号：复包络重采样算法中的插值器采用图3和表1中的方法实现；多普勒频偏模型在发射信号延时的基础上附加一个与径向速度对应的-105.6 kHz的多普勒频率。计算可得EVM2=0.22%，EVM3=129.36%。对于OFDM这种超宽带信号，不同子载波频率成分在接收信号中引起的多普勒频率差异较大，简单附加单一多普勒频率的模拟方法会产生非常大的误差，无法准确模拟目标信号包络的时间比例变化，已经完全丧失了模拟效果，而复包络重采样算法的模拟效果要明显更优。针对具体设计采用更优的插值器结构，比如可变系数Farrow结构滤波器，理论上还能实现更好的模拟效果。

2.2 包络伸缩特性分析

在上述情况下，据前文所述，接收信号在产生时延的同时包络会被展宽。以一个OFDM符号中的同相支路为例，忽略初始时延的影响，基准信号和两种方法产生的模拟信号的时域对比如图5所示。一个OFDM符号包含16 384个采样数据，在特定初始距离和运动速度条件下，复包络重采样算法产生的目标模拟信号包含了包络上的变化，一个符号内的采样数据扩展为16 387个，与基准信号相同。而多普勒频偏模型只是简单地延时并附加多普勒频偏，显然无法模拟这种超宽带目标信号特点，单个OFDM符号内仍只有16 384个数据。发射源与观测站之间朝靠近方向运动时包络会被“压缩”，情况同理。

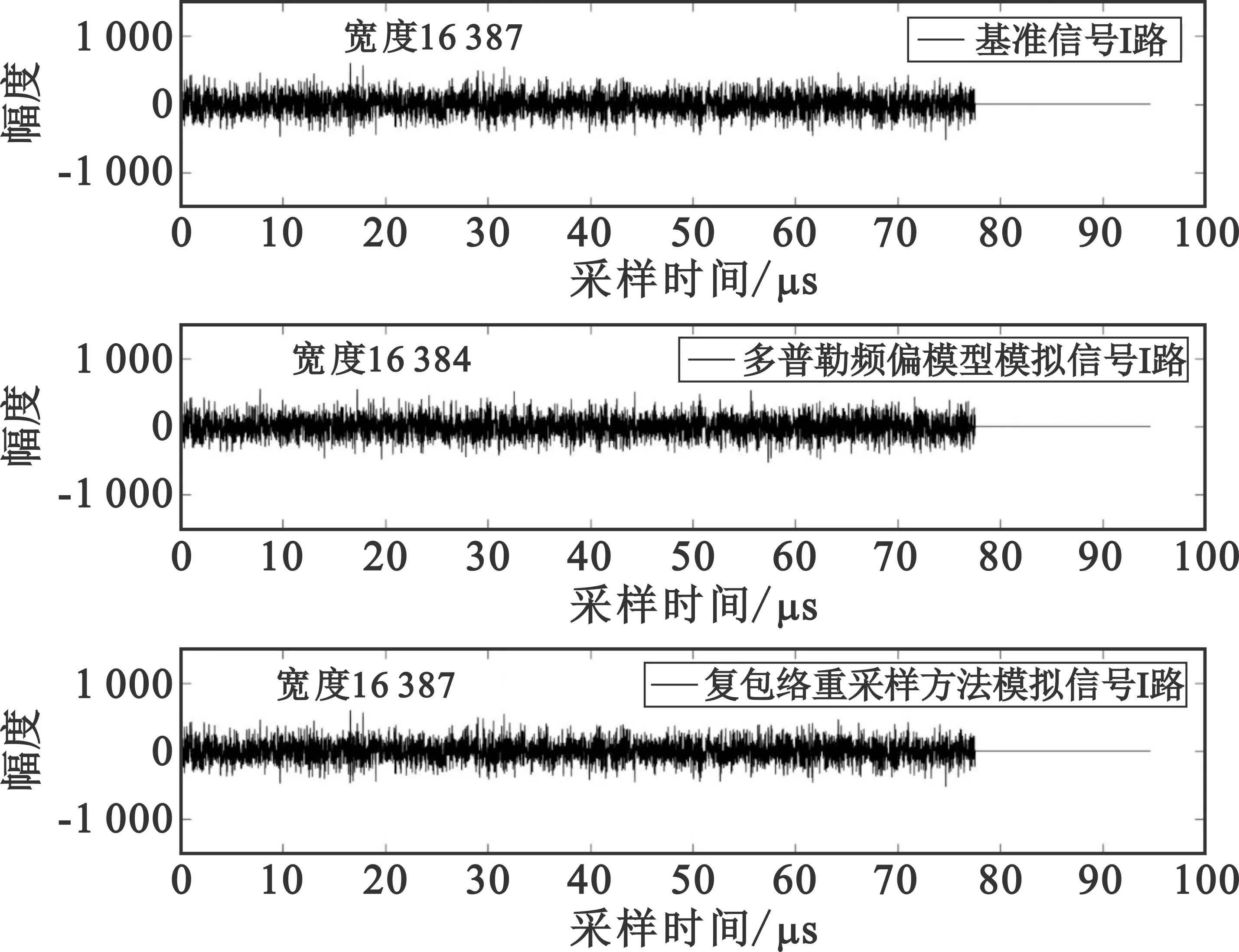
图5 窄脉冲发射信号和接收模拟信号时域对比

2.3 时变多普勒特性模拟

第二种情况，验证复包络重采样算法对目标信号中时变多普勒特性的模拟效果。假设目标初始处于静止状态，运动模型选择匀加速模型。Wigner-Ville分布可得到复杂时变信号的时频分布[14]，局部聚集性好。信号s(t)的Wigner-Ville分布计算公式为

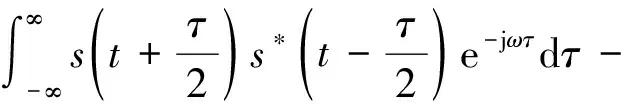
(17)

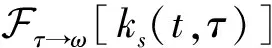
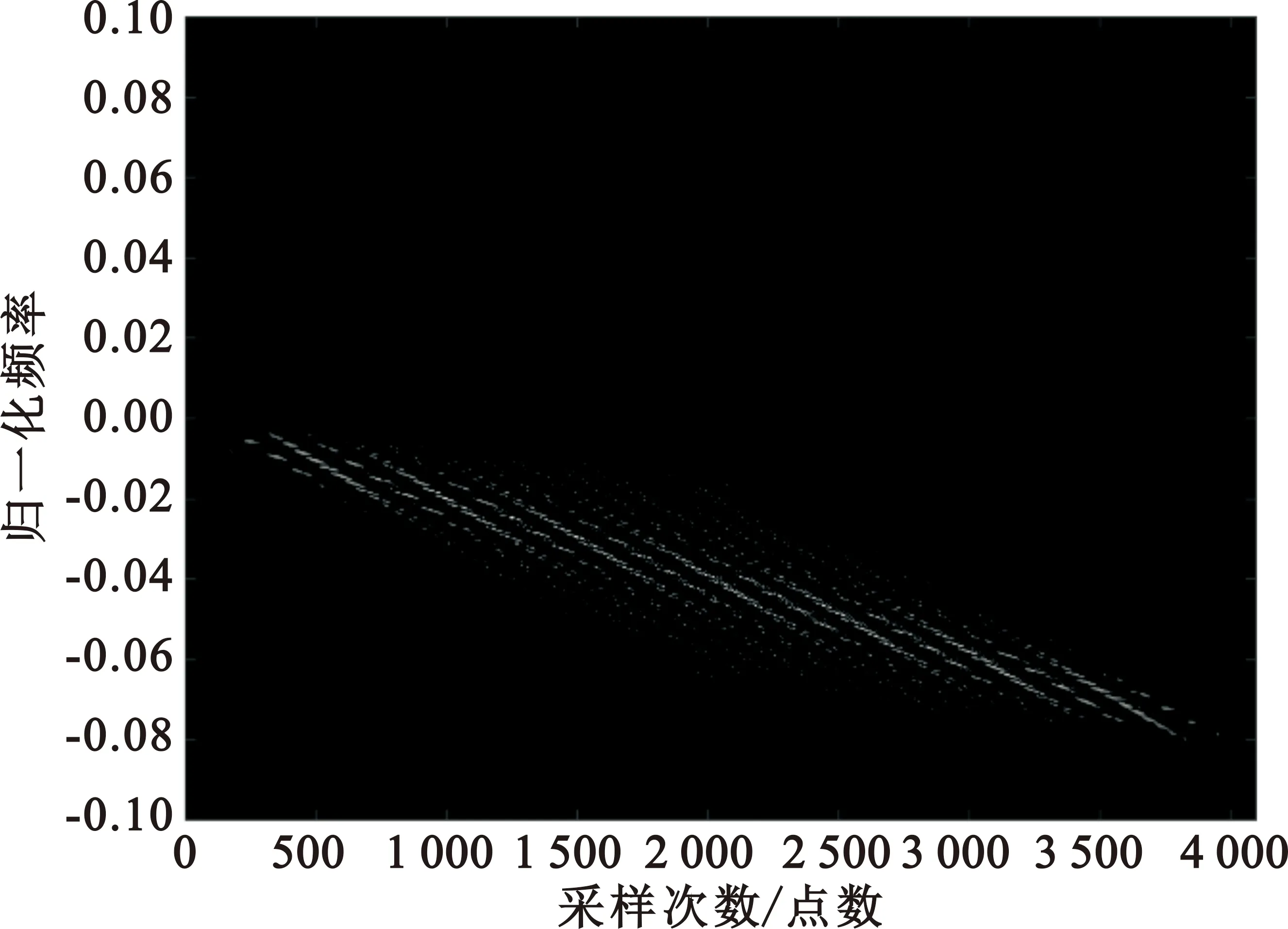
(a)多普勒频偏模型

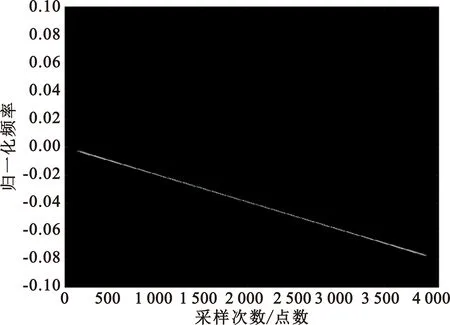
(b)复包络重采样算法图6 信号模拟时频分析(距离远离)

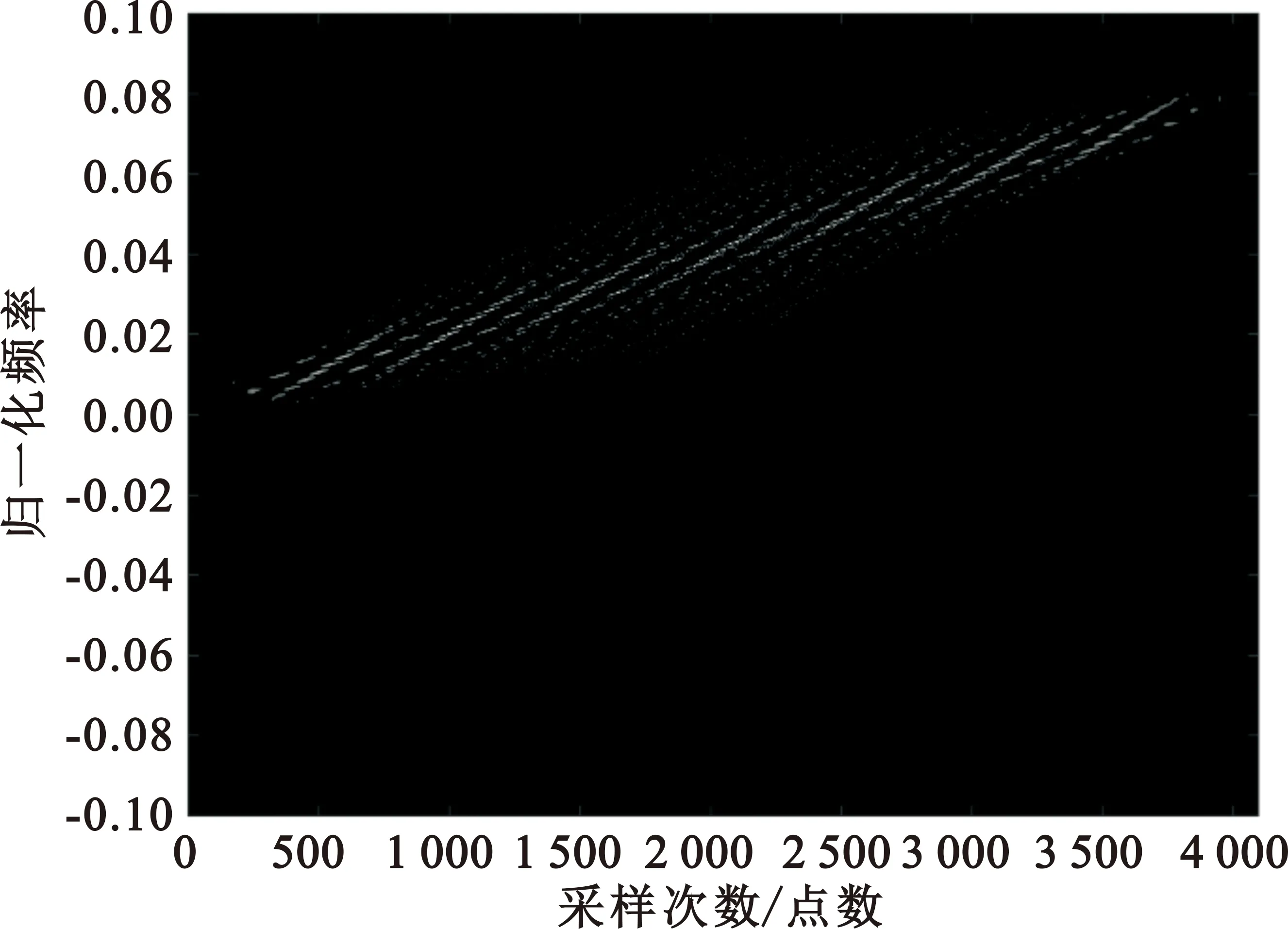
(a)多普勒频偏模型

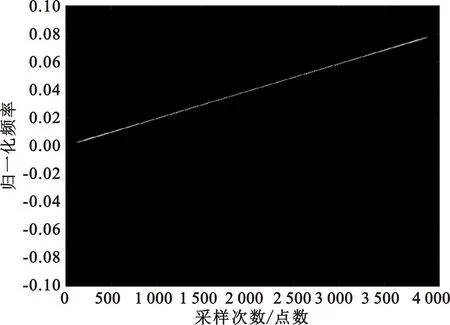
(b)复包络重采样算法图7 信号模拟时频分析(距离靠近)

由上可见，对时变多普勒模拟效果的偏差以及复包络畸变模拟的缺失，是造成多普勒频偏模型在模拟超宽带目标信号时产生较大误差的原因，而这也是基于复包络重采样算法的信号模拟器的独特优势。

3 结束语

本文提出了复包络重采样算法，针对超宽带高动态目标信号模拟，结合Farrow结构内插滤波器设计了一种新型的信号模拟方法。对比传统多普勒频偏模型和本文方法的实现原理可以发现，本文提出的信号模拟方法从时域调整和任意精度内插的角度出发，直接对目标信号的复包络序列进行重采样，不仅保留了多普勒频偏模型中时间和速度严格相关的优点，还保留了目标信号中包含的初始相位特性，能够有效地模拟目标信号的时变多普勒特性和复包络在传播过程中产生的畸变。当今系统越多越多地用到超宽带信号，在标校设备中采用本文提出的模拟方法可达到更贴切实际的验证效果，值得深入研究。