一种改进的多源信息融合室内定位方法*
刘期烈,万志鹏,周文敏,陈 澄
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
随着物联网、智慧城市的兴起,基于位置服务(Location Based Service,LBS)的应用在人们的生活中变得愈发重要[1]。LBS的关键是获取移动设备的精确位置信息,从而实现导航服务,如目标查找、路径规划等[2]。为了解决室外定位技术在室内场景的局限性,研究人员提出了多种室内定位技术,比如红外线定位、超声波定位、WiFi 定位、蓝牙定位等[3],但这些定位技术只能达到分米级定位精度且受环境影响较大。而超宽带(Ultra-wideband,UWB)定位技术定位精度可以达到厘米级,惯性测量单元(Inertial Measurement Unit,IMU)定位技术利用内部传感原理不受外界环境干扰,因此UWB和IMU定位技术相比于上述定位技术有显著的优势[4]。
UWB定位技术凭借其定位精度高、传输率高、功耗低等特点,十分适用于室内定位领域。但是在室内复杂环境下,UWB定位技术容易受到非视距(Non-line of Sight,NLOS)环境影响,信号通过障碍物时产生的附加延迟会降低定位精度。而IMU集成了加速度计、陀螺仪等传感器,可以测量加速度、角速度等运动状态信息。根据上述测量信息,就可以通过行人航迹推算(Pedestrian Dead Reckoning,PDR)算法[5-6]对位置进行解算。但是IMU器件本身存在测量误差,且由于IMU定位使用的是相对位移,会造成误差的累积。
使用单一定位系统进行定位仍然存在很大的局限性,无法实现复杂室内环境下的高精度定位。文献[7-10]对不同组合定位系统的定位性能进行了研究,其中UWB与IMU组合定位由于其定位精度高和优势互补的特性,已经成为了组合定位的较好选择。上述融合定位方式可以分为两种:第一种方式利用信息冗余完成对单一定位数据的修正,但是这样信息融合度比较低,使得定位精度不够高;第二种方式使用多种滤波算法对两种定位数据进行融合,但是当其中一种定位数据误差较大时会导致融合定位精度变低。然而,针对上述两种融合定位的缺陷,还没有文献进行深入、全面的研究。
因此,本文提出了一种将两者结合的改进融合定位模型。首先在UWB测量模型中引入了差分气压计,利用其高度信息对UWB定位结果进行修正。然后在融合算法中引入IMU累积误差判定门限,并使用卡尔曼滤波算法对UWB和IMU定位数据进行融合,使得最终可以在复杂的室内环境中获得较高的定位精度。
本文的主要贡献如下:一是在UWB测量模型中引入了差分气压计,并提出了一种差分加权UWB定位算法,降低NLOS环境对UWB定位的影响;二是在融合算法中引入IMU累积误差门限,通过阈值判定提高融合定位精度;三是用UWB定位系统和IMU定位系统在NLOS环境中测试,获得真实的测量数据,并在Matlab中使用所提的算法对测量数据进行位置解算,以此来评估该算法的定位效果。在实际NLOS环境测试中,对于UWB测量模型,差分加权定位算法在定位精度上相比于三边定位算法提高了38.09%;对于融合定位,在长时间进行定位时,改进融合定位模型在定位精度上相比于基础融合定位模型提高了45.71%。
1 系统建模
本节对UWB/IM融合定位系统进行建模,该系统首先使用UWB定位技术、IMU定位技术进行单一定位,然后将两者数据通过卡尔曼滤波器进行融合,可以有效地将两者的优势进行互补,最终可以得到鲁棒性高且更准确的定位结果。
1.1 UWB测量模型
信号到达时间(Time of Arrival,TOA)是UWB定位常用的定位方法,该方法是基于测距完成定位的。而基于测距完成的定位算法中,最常用的有三边定位算法和最小二乘定位算法。
在理想环境下的二维平面内,根据三边定位算法,以三个基站作为圆心,以基于TOA测得的基站与标签距离作为半径,可以画出3个圆并交于一点,交点就是标签所在位置,如图1所示。
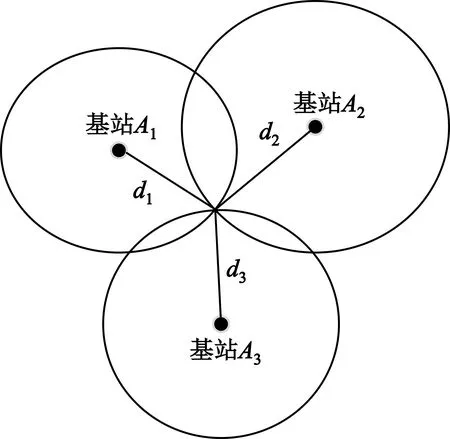
图1 理想情况下的TOA方法

(1)
但是实际上室内环境比较复杂,当对室内人员或者物品进行定位时,常常是LOS与NLOS混合的环境而不是单一的LOS或者NLOS环境。受NLOS影响,TOA测距值比真实值大,使得由测距值得到的3个圆不能相交于一个点,而是相交于一个区域,如图2所示。这时可使用最小二乘法求解目标最优估计位置。

图2 NLOS影响下的TOA方法
将方程组(1)扩展到N个基站,并用第2~N个等式分别减去第1个等式,可得方程组(2):
(2)
可转换成矩阵形式:
AX=b,
(3)
(4)

(5)
(6)
利用最小二乘法求解,可得到位置的估计值
(7)
1.2 IMU测量模型
IMU定位技术把牛顿力学当作基础,IMU通过集成的陀螺仪获取当前采样点下载体的角速度信息,并通过该值来解算加速度计与导航坐标系的相对方向角,进而得到当前采样点下载体的运动姿态和航向角等信息。同时,通过加速度计可以获取在载体坐标系下当前采样点的加速度信息,再使用姿态矩阵进行坐标系的转换并去除重力加速度的影响,即可获得在导航坐标系下当前采样点的载体加速度。然后对加速度进行一次积分和二次积分,分别得到当前采样点相对于上一采样点的速度、位移,再以上一采样点的速度和位置为基础,最终得到当前采样点下的速度和位置,如下式所示:
(8)
式中:a为导航坐标系下的加速度,ω为陀螺仪测得的角速度,t为运动时间,v0、s0和θ0分别表示目标在上一采样点的速度、位移和运动方位角,v1、s1和θ1分别表示目标在当前采样点的速度、位移和运动方位角。
IMU的定位精度取决于其加速度计和陀螺仪等传感器件的测量精度,测量加速度和角速度而产生的微小误差,会分别在一次积分、二次积分获得速度、位置的过程中累积。同时因为IMU积分计算得到的是相对位移,即当前采样点的位置信息是由基于上一采样点的位置信息计算得到的,所以位置误差会随时间累积,长时间下来会因为该误差过大而导致位置信息无法使用。
1.3 数据融合算法
常见的UWB/IMU融合定位模型如图3所示。分别通过UWB与IMU测量模型得到单一定位值,两者差值即卡尔曼滤波器观测向量。将观测向量输入卡尔曼滤波器得到IMU定位误差估计值,再用来对IMU测得定位值进行补偿,即可获取最终定位结果。
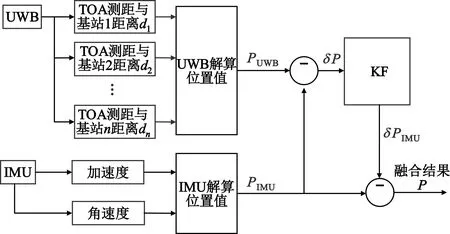
图3 UWB/IMU融合定位模型
下面对上述融合定位模型中的融合算法进行推导,主要对其中的状态向量、状态方程、观测向量以及观测方程进行描述。由于本文UWB与IMU仅在二维平面内进行信息融合,不涉及高度,因此各参数只考虑两个元素(x和y)。
状态向量是IMU定位时的速度误差和位置误差,即
Xk=[δpk,xδpk,yδvk,xδvk,y]T。
(9)
式中:(δpk,x,δpk,y) 是位置误差,(δvk,x,δvk,y) 是速度误差。
状态方程为
Xk+1=FXk+wk。
(10)
式中:wk是系统噪声,且wk~N(0,Qk),Qk是状态转移噪声协方差矩阵;F是状态转移矩阵,

(11)
式中:Δt是采样周期。
观测向量是IMU解算的坐标与UWB解算的坐标的差值,即
(12)
观测方程为
Zk=HXk+nk。
(13)
式中:nk是测量噪声,且nk~N(0,Rk),Rk是观测噪声协方差矩阵;H是测量矩阵,
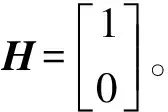
(14)
基于状态方程和观测方程,即可使用卡尔曼滤波算法进行时间更新和观测更新,完成数据融合。具体步骤如下:
首先对状态向量和误差协方差进行预测:
(15)
Pk+1|k=FPkFT+Qk。
(16)
然后计算卡尔曼增益:
Kk+1=Pk+1|kHT(HPk+1|kHT+Rk)-1。
(17)
最后对状态向量和误差协方差进行更新:
(18)
Pk+1=(I-Kk+1H)Pk+1|k。
(19)
2 改进的融合定位模型
本文提出的改进融合定位模型如图4所示,在图3融合定位模型上进行了两步改进:首先在模型中引入了差分气压计,使用其在高度信息上的冗余对UWB测量模型进行优化;然后在融合算法中引入了IMU累积误差判定门限,对IMU所受累积误差进行判定,对融合算法进行优化。
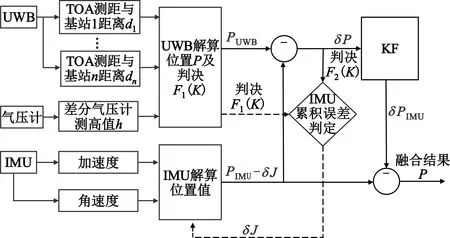
图4 改进的融合定位模型
2.1 UWB测量模型优化
上述使用最小二乘法解算位置,其实是默认为所有测距值赋予相同的权重,而显然每个测距值受NLOS误差影响程度不一样。应该对每个测距值所受误差大小进行判定,对误差小的测距值赋予较大的权重,对误差大的测距值赋予较小的权重。
本文提出了一种通过差分气压计测高的方法来对测距值所受误差大小进行判断,然后即可根据所受误差大小对不同测距值赋予不同权重,再使用加权最小二乘法来求解最优位置估计值,即采取NLOS鉴别及误差削弱的方法削弱NLOS对测距的影响。
2.1.1 NLOS鉴别

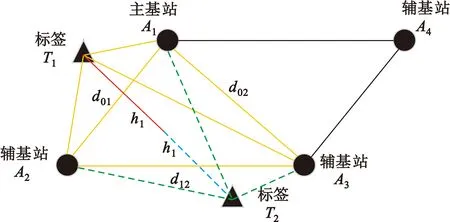
图5 标签两个解关于基站平面对称
(20)
再将这些四面体解算出的标签高度hm与差分气压计测得标签高度hbar进行比较,得到每个组合的高度差值δhm,以此作为每个基站组合测距受NLOS误差影响情况。
2.1.2 降低NLOS误差影响
|δh(k)|=|h(k)UWB-h(k)bar|,
(21)
(22)
式中:λ1表示经验阈值;h表示气压计测高精度,本文使用的气压计模块为SPL06-001,该模块在高线性模式下的测高精度可达5 cm[13]。
此时分为两种工作模式,下面分别介绍。
(1)F1(k)=1
若F1(k) 的值为“1”,判定UWB定位较准,此时直接选择此种定位结果所得到的二维坐标(x,y),加上差分气压计所得高度hbar,得到三维定位结果(x,y,hbar)。
(2)F1(k)!=1
通过测距解算出的高度确定每个测距值的权值,并通过加权最小二乘法得到二维定位坐标(x,y) ,加上差分气压计所得高度hbar,得到三维定位结果(x,y,hbar)。具体过程如下:
首先,求每个基站参与的组合的高度差值之和,再除以个数,即可得到每个基站参与造成的平均高度差δhi,然后根据该差值即可确定该基站测距值的可信度βi:
βi=1/δhi。
(23)
然后,已知标签与每个基站三维测距值di3d,使用勾股定理(式(24))即可得到标签与每个基站测得的水平距离di2d:
(24)
最后,类比式(7),可以求解加权最小二乘的标签位置估计值
(25)
式中:
(26)
2.2 融合算法优化
IMU在长时间进行定位时漂移误差会导致较大的累积误差。UWB和IMU分别完成定位后,将这两个定位结果相减,将该差值δP(k)作为观测量输入卡尔曼滤波之前,可求其绝对值并对该值进行判断:
|δP(k)|=|P(k)IMU-P(k)UWB|,
(27)
(28)
式中:λ2表示经验阈值;p表示UWB与IMU平均定位误差之和,在NLOS环境下短时间内,UWB与IMU的平均定位误差分别为26 cm、22 cm。
若F2(k)的值为“1”,判定此时UWB与IMU定位结果相差较大。若同时有F1(k)的值为“1”,则说明此时UWB定位结果比较准确,IMU定位结果累积误差较大。可引入矫正因子δJ,其大小为k时刻IMU与UWB定位差值:
δJ=P(k)IMU-P(k)UWB。
(29)
因此,在k+1时刻及之后的IMU测量值都要引入该矫正因子:
P(k+1)IMU=P(k+1)IMU-δJ。
(30)
对应地,要在k+1时刻及之后的观测向量中引入矫正因子:
(31)
在融合算法中引入IMU累积误差判定门限可以对IMU测量误差进行判别,进而在IMU测量值以及融合算法的观测向量中引入矫正因子,最终得到精确的融合定位结果。
3 仿真与分析
本文使用的是基于DW1000芯片的Decawave套件,该套件主要由4个基站1个标签组成,采用双向测距(Two Way Ranging,TWR)方法来进行测距,数据刷新率可达10 Hz。另外,主基站上扩展了无线WiFi模块来实现主基站与上位机的无线通信,可在上位机显示实时轨迹。
使用的惯导模块是由荷兰Xsens公司开发的MTI600,该模块集成了三轴加速计,测量范围±10g,可以测得三维加速度值;同时集成了三轴陀螺仪,测量范围±2 000 °/s,可以测得三维姿态角,其数据刷新率可达1 000 Hz。另外,该模块体积小、精度高,非常适合与UWB模块进行融合定位。该模块具体参数如表1所示。

表1 IMU的性能参数
同时,在UWB模块上集成了气压计模块SPL06-001,该模块测高分辨率很高,在高线性模式下可以达到0.006 hPa(5 cm)。同时可以通过差分气压法,即在标签和主基站上都集成了该气压计模块,这样可以对气压计偏差进行校准,获得更为准确的测压信息,进而得到较为准确的标签高度信息。
本文定位实验选在重庆邮电大学信科大厦2楼大厅,场地大小为3.6 m×5.4 m,如图6所示。为了验证本文提出的优化方法,分别对UWB定位、融合定位进行测试实验。

图6 测试环境
3.1 UWB测量模型对比实验
由上述分析可知,UWB定位受NLOS测距影响较大,因此这里在NLOS环境下对UWB分别进行静态和动态定位实验。
3.1.1 静态实验
此处实验将待测标签放在图6所示环境的水平地面上,并分别在如表2所示8个点放置10 s进行数据采集,开展NLOS环境下的UWB静态定位实验。表2所示为NLOS环境下静态测试点性能统计结果。
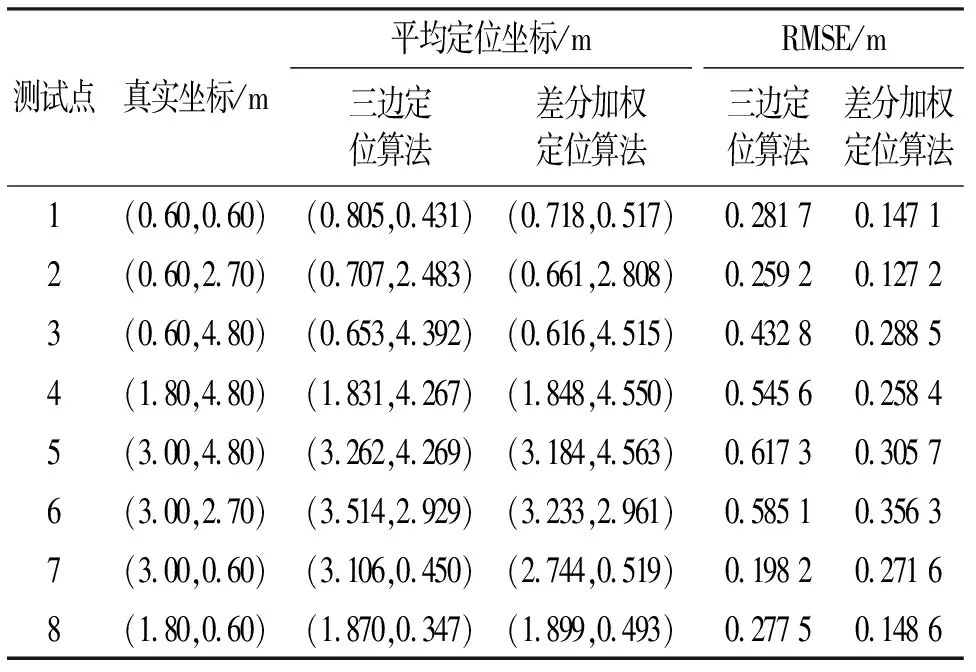
表2 UWB在NLOS环境下静态定位
由表2可知,在NLOS环境下进行静态点定位,三边定位算法的均方根误差最小值为19.82 cm,最大值为61.73 cm,平均定位误差为39.97 cm;差分加权定位算法的均方根误差最小值为12.72 cm,最大值为35.63 cm,平均定位误差为23.79 cm。可以发现,UWB定位精度受NLOS环境影响较大,而本文提出的差分加权定位算法相比于三边定位算法定位精度提高了40.04%,具有较好的抗NLOS能力。
3.1.2 动态实验
此处实验让行人手持UWB模块放在身前,然后在图6所示测试环境下按预定轨迹行走,开展NLOS环境下的UWB动态定位实验。
图7所示为NLOS环境下两种定位方法的UWB定位轨迹,表3所示为UWB动态定位误差。

图7 NLOS环境下UWB动态定位

表3 UWB动态定位误差
结合图7和表3可知,在NLOS环境下,使用三边定位算法的X、Y轴最大误差分别为50.27 cm和69.08 cm,X、Y轴平均误差分别为20.51 cm和32.49 cm,平均定位误差为42 cm;使用差分加权定位算法X、Y轴最大误差分别为34.48 cm和44.84 cm,X、Y轴平均误差分别为13.17 cm和17.29 cm,平均定位误差为26 cm。差分加权定位算法相比于三边定位算法在定位精度上提高了38.09%,可以对UWB受到的NLOS误差进行有效削弱,得到与真实路线更吻合的轨迹。
3.2 融合定位对比实验
由3.1节可知,UWB定位受NLOS环境影响较大,此处使用UWB与IMU进行数据融合,进一步降低UWB受NLOS环境的影响。由于本文进行三维定位时的高度信息由集成在UWB模块上的气压计模块提供,而UWB模块与IMU模块仅在二维平面内进行信息融合,因此可以忽略UWB模块与IMU模块在高度上的差异。让实验人员手持UWB模块放在身前,并将IMU模块放置在脚尖,然后在图6所示测试环境下按预定轨迹行走,开展NLOS环境下的短时间和长时间融合定位实验。
3.2.1 短时间融合定位实验
图8所示为与图7相同条件下的短时间融合定位轨迹。结合图7可知,在NLOS环境下进行短时间定位时,IMU平均定位误差为22 cm,此时三边定位算法的平均定位误差为42 cm,融合定位平均定位误差为28 cm;差分加权定位算法的平均定位误差为26 cm,改进融合定位平均定位误差为19 cm。可以看出在NLOS情况下,融合定位比单一UWB定位方法的定位精度更高,更符合实际行走轨迹。
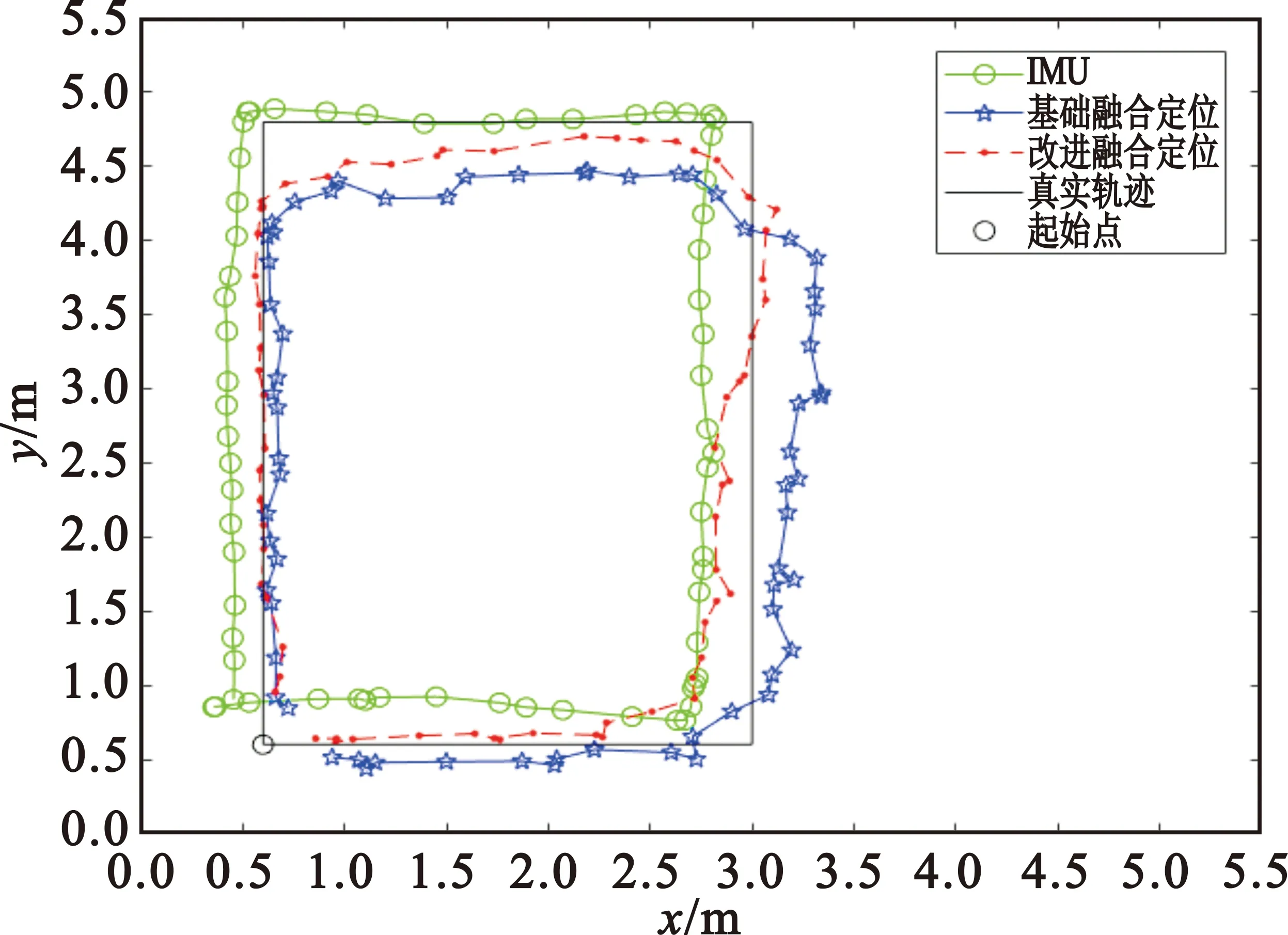
图8 短时间融合定位
另外可以发现,在短时间NLOS环境下进行融合定位,UWB受到NLOS距离的影响导致定位误差较大,而IMU不受环境影响且在短时间内定位精度较高,因此在这种情况下,UWB不仅不能对IMU起到修正作用,基础融合定位反而会取得比单一IMU定位更差的定位效果。而对于改进融合定位,由于降低了UWB受到NLOS距离的影响,可以得到更高的UWB定位精度,因此改进融合定位可以对短时间内IMU定位起到一定的修正效果;相比于基础融合定位,改进融合定位可以在定位精度上提高32.15%。
3.2.2 长时间融合定位实验
如图9所示为绕预定轨迹行走多圈即长时间行走之后,两种融合定位方法轨迹对比。表4所示为两种融合定位方法的定位误差。
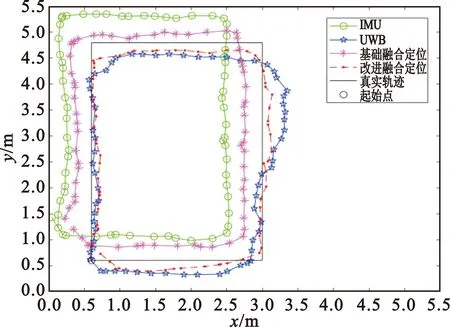
图9 长时间融合定位

表4 融合定位误差
由图9可知,在长时间行走后,差分加权定位算法得到的UWB平均定位误差为27 cm,定位效果与之前相差不大;而IMU平均定位误差为60 cm,可以看出该误差远大于短时间行走时的IMU平均定位误差。这是因为IMU定位存在累积误差,也说明了对IMU累积误差进行削弱的必要性。
结合图9和表4可知,对于基础融合定位,X、Y轴最大误差分别为46.71 cm和41.23 cm,X、Y轴平均误差分别为26.35 cm和23.78 cm;对于改进融合定位,X、Y轴最大误差分别为26.48 cm和31.74 cm,X、Y轴平均误差分别12.25 cm和16.52 cm。
另外可以发现,对于基础融合定位,不仅UWB定位精度受NLOS测距影响大大降低,IMU定位产生的累积误差也很大,导致基础融合定位方法定位效果较差,平均定位误差为35 cm。因此对于改进融合定位方法,可以在优化UWB测量模型的基础上,在融合算法中引入矫正因子,动态纠正IMU累积误差,就能获得更好的融合定位效果,平均定位误差为19 cm。改进的融合定位模型相比于基础融合定位模型,定位精度提高了45.71%。
另外,在融合定位模型中引入矫正因子,只需要进行常数次运算,时间复杂度为O(1),故改进的融合定位模型可以满足定位实时性要求。
4 结束语
单一UWB定位系统存在很大的局限性,无法适用于大多数场景,如隧道定位、超市导航等,因此本文提出了一种UWB/IMU融合定位的优化方法。首先,针对UWB定位时受NLOS误差影响大,提出了一种差分权值定位算法,并在NLOS环境中进行静态和动态定位对比实验,验证了该算法比三边定位算法具有更高的精确度。然后,针对IMU定位时受累积误差影响大,在融合算法中引入IMU测量值矫正因子,并在动态NLOS环境下进行融合定位对比实验,验证了在融合算法中引入矫正因子可以进一步提高融合定位的精度,使得最终可以在复杂的室内环境中,获取一个较为准确的融合定位结果。
但本文使用的方法存在两点需优化之处:一是在融合定位中进行的改进,主要针对于单一定位精度及融合模型中的测量值,可以进一步对融合时使用的卡尔曼滤波算法进行改进;二是使用多源信息进行融合定位,功耗会比单一系统更高,可以考虑利用UWB、IMU的测量信息实现睡眠机制,来保证整个系统的续航能力。

