联合多脉冲检测的PSWF正交调制信号盲自适应均衡*

钟佩琳,胡 昊,刘佳琪,刘传辉

(海军航空大学 a.航空基础学院；b.信号与信息处理山东省重点实验室，山东 烟台 264001)

0 引 言

2011年，Sacchi等人[1]提出将基于椭圆球面波函数(Prolate Spheroidal Wave Function，PSWF)的 4阶脉冲波形调制方法用于W频段卫星通信，并通过W频段静止轨道下行链路测试，证明了该方法相对于升余弦滤波的正交幅度调制方法具有更高的功率效率和抗非线性失真能力，相比于恒包络高斯最小频移键控方法具有更高的频谱效率和更好的差错性能。该项研究开创了基于PSWF的正交脉冲调制方式在卫星通信应用的先河。实际上，文献[1]中的方法并未对PSWF的其他参数进行有效利用，频带利用率仍然较低。基于PSWF的时域正交调制方法利用频谱交叠脉冲组的良好正交性，可在加性高斯白噪声的信道中获得理论上的最佳频带利用率[2-3]。在卫星通信高速数传相关项目研究中，分析发现卫星信道特性由于复杂且时变[4-5]，对PSWF调制信号正交性产生了较为严重的破坏，带来严重的码间干扰和脉冲间干扰，降低了通信可靠性。系统想要获得较高的有效性，必须先保证传输的可靠性，因此，在系统中加入一定的信道补偿算法必不可少。

信道均衡是应用较为广泛的信道补偿方法。由于卫星信道具有时变特性，均衡算法须要具有跟踪调节能力，也即自适应能力。目前，从自适应模式上，均衡算法可以分为三种基本模式：一是基于训练的自适应均衡算法[6]；二是基于判决引导技术的自适应均衡算法[7]；三是基于盲技术的自适应均衡算法[7-9]。第一种模式简单易行，但需要发送序列，信息传输效率低；第二种模式不需要训练序列，但在信号失真较大时，会使均衡器虚假收敛到局部极小值；前两种模式通常结合使用，即所谓半盲方法，先发送训练序列进行参数初始化，待系数充分收敛后，切换到判决引导模式；第三种模式利用信号的有限统计信息来均衡信道，不需要训练序列，但复杂度高，补偿精度不如非盲算法。

实际上，单独依靠均衡器对消除码间干扰和脉冲间干扰的效果有限，若均衡器阶数设置不当，还会引入额外干扰。此外，PSWF时域正交调制信号通常采用相关检测法，把一切干扰都当作噪声来对待，无法充分利用多脉冲干扰中的有用信息。在前期研究中，笔者所在团队曾将多用户检测技术[10-12]转化为多脉冲检测技术[13]，用以消除PSWF时域正交调制信号的脉冲间干扰，在精确的信道估计基础上，较传统的相关检测可以获得更好的误码性能。与均衡技术不同，多脉冲检测技术的出发点不是补偿信道特性，而是充分提取脉冲干扰中的有用信息，助力信息正确检测。然而，前期的研究仅讨论了基于信道估计的多脉冲检测，对于复杂恶劣的信道条件，需频繁进行训练，浪费带宽资源，也影响检测性能。

由上述分析可知，信道均衡与检测各有作用和优势，也各有短板。本文将两种技术结合起来，提出一种联合多脉冲检测的盲自适应均衡方法，利用多脉冲检测消除脉冲间干扰的能力降低均衡模块的阶数及算法难度，同时，利用均衡模块对信道的部分补偿作用为多脉冲检测改善信道环境。此外，联合算法具有盲自适应能力，既可以更好地适应动态环境，又可以降低训练复杂度和计算复杂度。算法性能分析和仿真中所采用的卫星信道模型为加拿大通信研究中心的Loo等人[14-15]提出的Ka频段卫星通信信道统计模型，该模型受到学术界的广泛认可和应用。

1 方法描述及算法流程

1.1 联合方法均衡器总体结构

联合算法的设计思路是，首先以采样速率对失真信号进行均衡，再送入多脉冲检测模块，消除多脉冲干扰后提取比特信息，然后利用提取的信息与模板脉冲重构信号码元，作为训练序列对均衡器模块参数进行训练，以此实现盲均衡。基于上述思路，提出一种联合多脉冲检测的盲自适应均衡方法(Blind Adaptive Equalization united with Multi-Pulse Detection,MPD-BAE),其结构如图1所示。

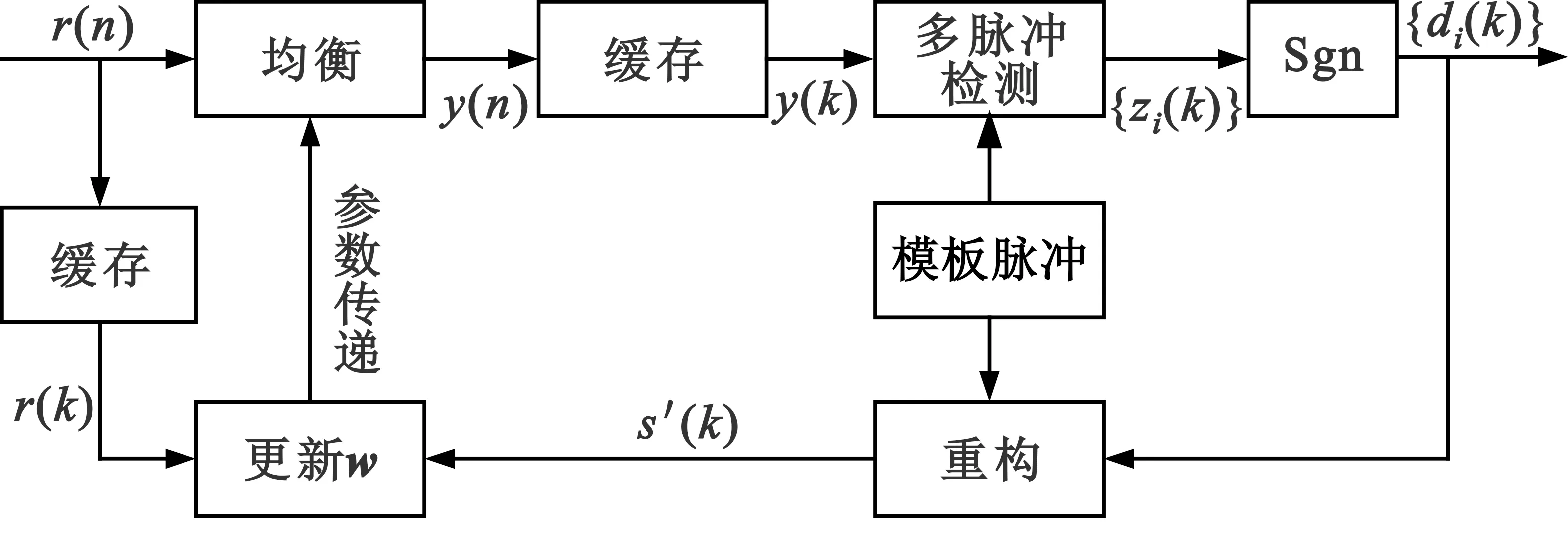
图1 MPD-BAE均衡器结构

该均衡器包含多个模块，除了均衡和多脉冲检测两个主要模块外，还有几个辅助模块：缓存模块的作用是存储当前输入信号码元各采样点值，以向量形式输出到下一模块；模板脉冲则为多脉冲检测模块和重构模块提供脉冲波形。图1中w=[w11,w12,…,w1M1]T表示线性均衡器抽头系数，M1为抽头个数，r(n)表示接收端的采样信号，每个码元包含N个采样点，r(k)=[r1(k),r2(k),…,rN(k)]T是经缓存后的第k个码元向量，y(n)表示采样速率线性均衡器的输出信号，y(k)=[y1(k),y2(k),…,yN(k)]T表示其第k个码元向量，{zi(k)}为多脉冲检测模块输出的第i路脉冲加载的第k个信息待判决值，s′(k)=[s1(k),s2(k),…,sN(k)]T为重构后的第k个码元向量。

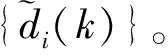
1.2 PSWF时域正交调制信号多脉冲检测原理

在介绍上述盲均衡算法具体流程之前，先简要介绍多脉冲检测器的工作原理。

在一个含有K个用户的基带码分多址(Code Division Multiple Access，CDMA) 系统中，由某一个给定用户接收到的连续时间波形可以表示为

(1)

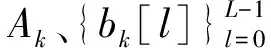
(2)

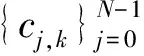
接收端收到的PSWF时域正交调制信号r(t)可表示为

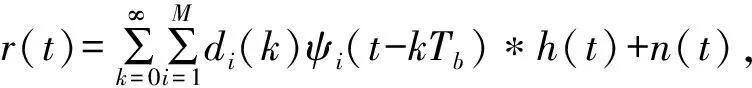
(3)

式中：ψi(t)为第i路PSWF脉冲，di(k)为该路脉冲携带的第k个比特信息，h(t)为信道时域响应，n(t)为加性高斯白噪声。

比较式(1)、式(2)和式(3)易看出，接收端的PSWF时域正交调制信号与直扩多用户CDMA信号具有非常相似的结构。第k路脉冲信号可以看作是第k个用户的信号波形，Ak=1，采样点数N相当于特征序列长度，只是特征序列的取值不再是±1，而是PSWF脉冲的采样值ψk=[ψk1,ψk2,…,ψkN]，即cj,k=ψk，其归一化能量为1，φ(·)恒为1。根据这种对应关系，即可将多用户检测转化为适用于PSWF时域正交调制信号的多脉冲检测方法。多脉冲检测器的任务是在已知各模板脉冲的情况下，检测出各路脉冲携带的信息。

目前，最常用的两种线性检测器形式是解相关检测器和最小均方误差(Minimum Mean Squared Error,MMSE)检测器[12]，前者以提高噪声为代价来消除脉冲间干扰，而后者使检测器的输出中脉冲间干扰和噪声的总体影响最小，因此，MMSE检测器具有比解相关检测器更好的性能。MMSE检测器一般用一个加权向量m∈N来描述，在多脉冲检测中，由于需要将所有M路脉冲加载信息检测出来，因此需要M个加权向量。假设第i个检测器表示为mi，其解可以由以下问题的最优解给出：

(4)

直接解式(4)，可得

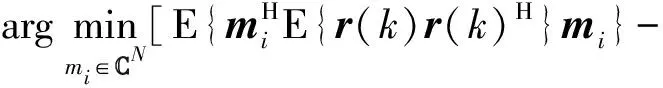
(5)

式中：

Cr=E{r(k)r(k)H}=ψψH+σ2IN

(6)

为接收信号的自相关矩阵，可由其相应样值的自相关估计出来，ψ=[ψ1,ψ2,…,ψM]是由脉冲列向量组构成的矩阵。

文献[11]提出一种多用户检测的子空间方法，基于用户特征波形张成的信号子空间进行估计，这种方法被证明大大优于式(5)的直接法[10]。将该方法应用到多脉冲检测中，其基本原理如下：

假设M路脉冲线性独立，且式(6)中矩阵Cr是秩为M的矩阵ψψH与σ2IN之和，矩阵Cr有M个严格大于σ2的特征值，剩下的N-M个特征值均等于σ2，其特征分解可写为

(7)

式中：Λψ包含了Cr的M个最大的特征值，Uψ为对应Λψ中M个最大特征值的M个正交特征列向量构成的矩阵，Un为N-M个特征值为σ2对应的正交特征列向量构成的矩阵。

由此，得到MMSE检测器的子空间形式为

(8)

当信号受到信道影响而产生失真时，输入信号自相关矩阵变为

(9)

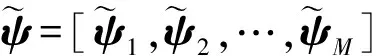
(10)

由此，得到MMSE多脉冲检测算法为

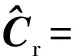
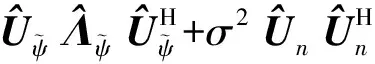
(11)

(12)

(13)

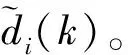
多脉冲检测器是盲均衡器的重要组成，提供信息比特估计值作为均衡器的训练序列，其性能对整个盲均衡器起到了决定性作用。

1.3 MPD-BAE方法的算法流程

MPD-BAE方法的算法流程和具体步骤如下：

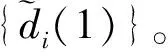
Step2k=2,3,…,L时，L为均衡模块参数达到收敛所需训练码元的个数，R(n)=[r(n-M1+1),…,r(n-1),r(n)]T，进行线性均衡：

(14)

缓存第k个均衡后的码元信号y(k)，y(k)=[y[(k-1)N+1],…,y(kN)]H，对其进行多脉冲检测：

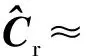
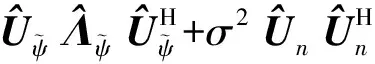
(15)

(16)

(17)

符号判决：

(18)

重构：

(19)

训练更新均衡器抽头系数，并传递给均衡模块：

(20)

wk+1=wk+2μe(n)R*(n) 。

(21)

式中：μ为参数w迭代的步长。

2 性能分析与仿真

2.1 算法性能分析

由于不同信道特性对信号的影响形式不同，有些甚至无法用表达式表示，为便于对联合多脉冲检测的盲自适应均衡器的性能进行理论分析，这里假设信道特性为线性。

2.1.1 输出信号干扰噪声比(Signal-to-Interference plus Noise Ratio,SINR)

输出SINR是衡量多用户检测性能的一个重要指标，多脉冲检测同样可以借鉴这一指标，只是需要考察多个加权向量，这里以第i路为代表进行分析。

对多脉冲检测器的输出式(17)进行整理得

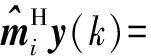
n[(k-1)N+j-M1+1:(k-1)N+j]}。

(22)

式中:第4个等号后第1项含有第i路信息，第2项为其余路脉冲的干扰，第3项为经过均衡和多脉冲检测后的噪声。

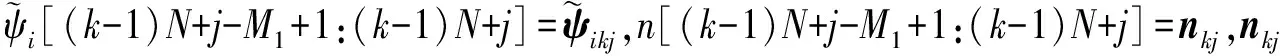
办理完入院手续，还没等喘口气，老婆便和王姐商量是不是应该给蒋利学送个红包。王姐也认为应该送。老婆问送多少，王姐说五百就行。可是没多久，两人便回来了。看两人神色，就知道红包没送成。一问，果不其然没送成。老婆便埋怨王姐，红包都扔他办公桌上了，不该再拿回来。王姐说，这人一看就是老倔驴，你不想想，他那么坚决，一但真不想收，一会儿拿着红包跑病房来还，咱们可咋下台？

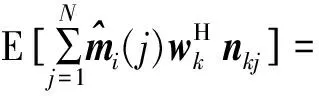
0，

(23)

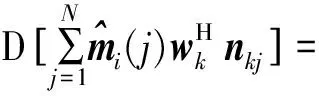
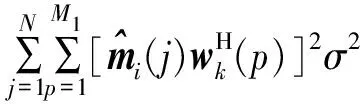
(24)

同时，根据式(22)中的信号项、干扰项和噪声项，可以得到多脉冲检测器的输出SINR为

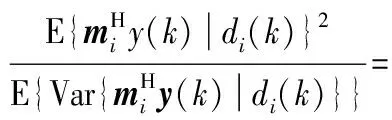
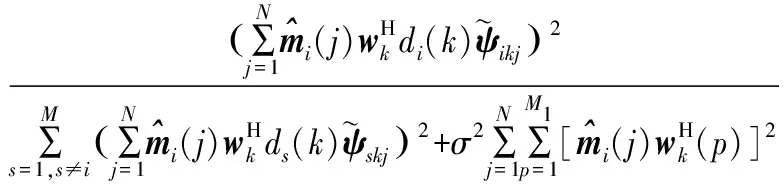
(25)

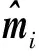
2.1.2 差错性能分析

根据噪声的分布特性可得第i路脉冲误比特率为

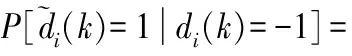
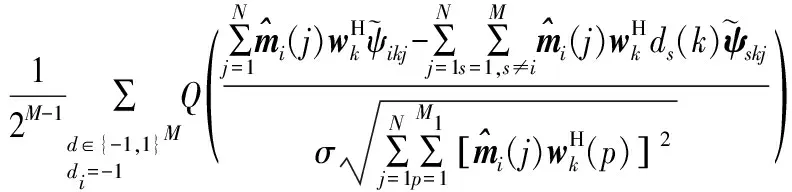
(26)

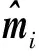
2.1.3 计算复杂度分析

根据MPD-BAE算法的具体实施步骤，得到主要计算过程的计算量，如表1所示，其中，N是码元采样点数。

表1 MPD-BAE计算复杂度

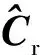
2.2 仿真与分析

本节将在卫星信道模型条件下对MPD-BAE方法的收敛性能和误比特率性能进行仿真。

信道采用Ka频段经典移动卫星信道统计模型——Loo模型，其中，环境参数设置为晴天轻度阴影衰落和中雨重度阴影衰落，参数取值见表2。采用MPD-BAE方法，均衡器阶数为M1=15，初始化w(M1)=1，其余为0，步长为0.01，多脉冲检测模块采用MMSE检测方法。PSWF时域正交调制信号频段为17～19 GHz，码元周期为4.5 ns，并行路数为16，码元内采样点数为50。收敛性能仿真中，Eb/No为15 dB，仿真平均次数为100。

表2 Loo模型参数

MPD-BAE均衡算法在晴天轻度和中雨重度阴影衰落信道下的收敛特性如图2所示。

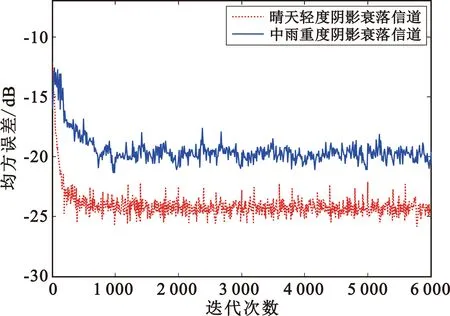
图2 不同卫星信道条件下MPD-BAE算法的收敛性能

从图2中可以看出，在天气状况比较良好、多径衰落不严重的信道条件下，MPD-BAE算法具有较好的收敛特性，在迭代约500次后达到收敛，收敛后均方误差约为-24 dB；在天气状况比较恶劣、多径衰落严重的信道条件下，MPD-BAE的收敛性能会下降，需要迭代约1 000次才能达到收敛，迭代的初始阶段误差起伏较为明显，稳态误差约为-20 dB。需要说明的是，这里的迭代次数是指采样点个数而不是码元个数。此外，容易看到，当信道条件较为恶劣时，所提盲均衡算法在迭代初期有一定的起伏，这是因为多用户检测初期存在一定的误差，需要若干码元的调整。

下面对MPD-BAE方法在以上两种卫星信道条件下的误比特率(Bit Error Rate,BER)进行仿真，并与前期提出的基于初始化参数传递的并行自适应均衡方法( Parallel Adaptive Decision Feedback Equalization based on Initialization Parameter Passing,IPP-PADFE)和采样速率线性均衡方法进行比较。这两种对比方法均需要发射端发送训练序列，仿真结果如图3所示。

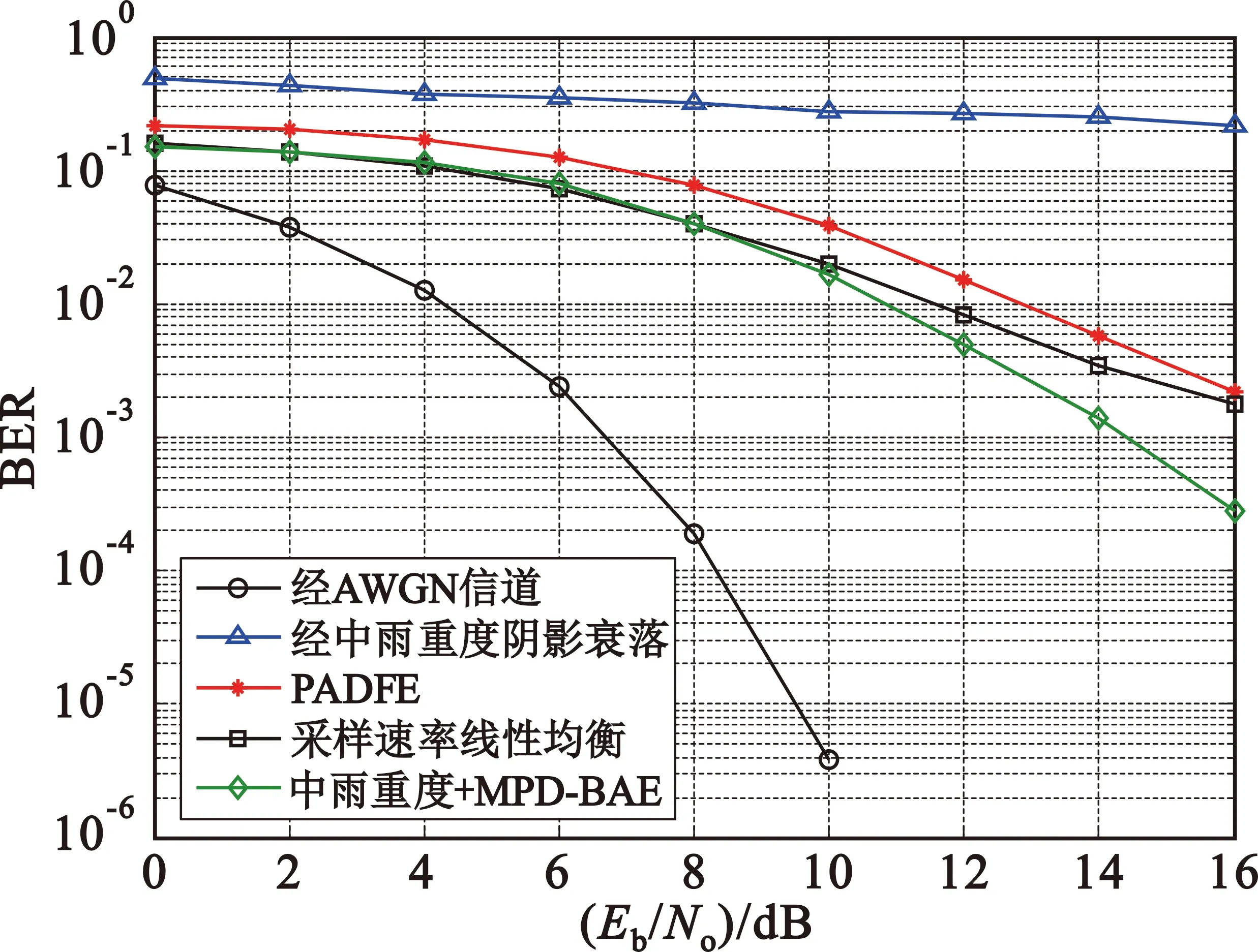
(a)中雨重度阴影衰落

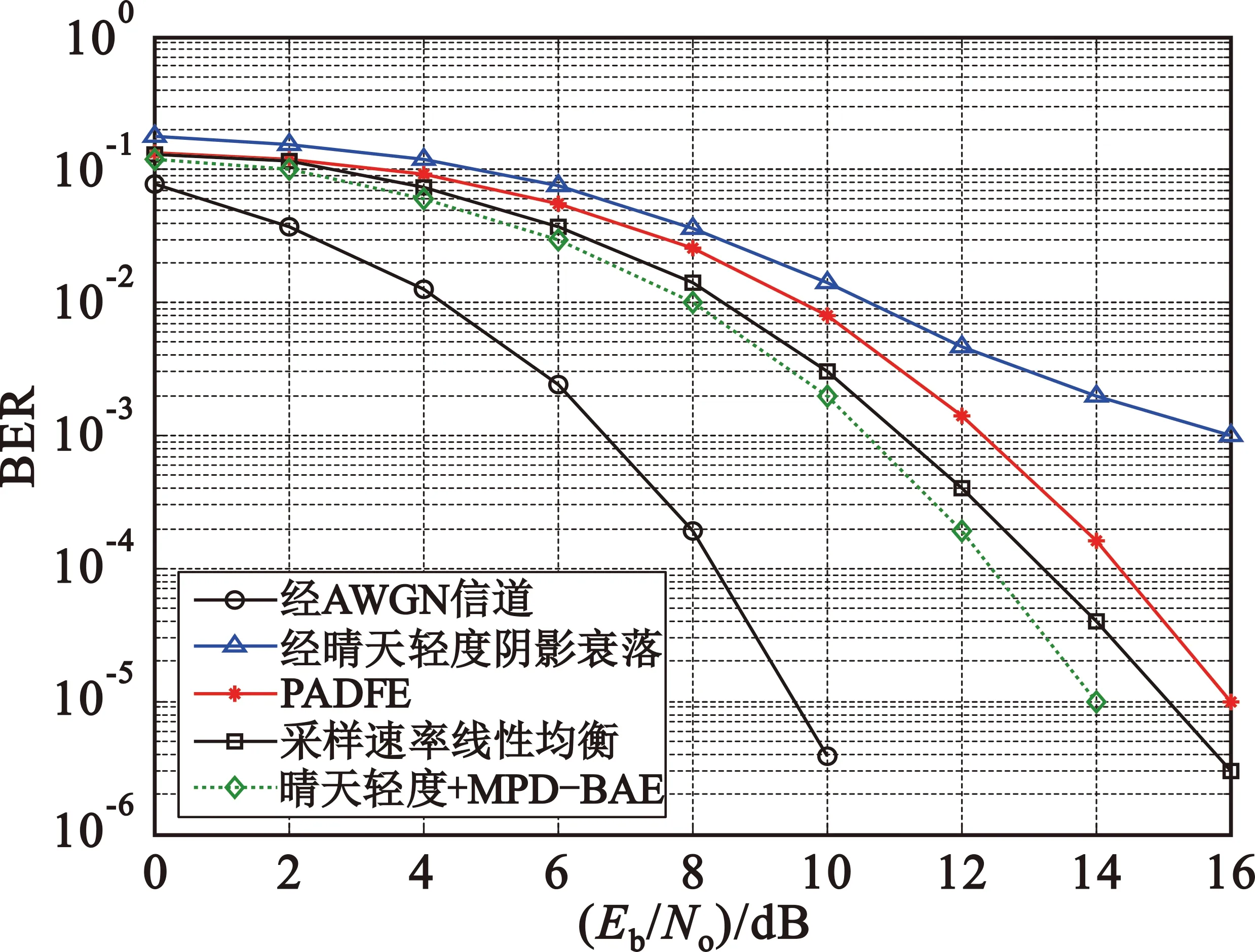
(b)晴天轻度阴影衰落

由图3可知，卫星信道特性给系统BER特性带来很大影响，在中雨重度阴影衰落信道条件下，系统BER几乎不随信噪比的提高而改善，显然噪声已经不是主要影响因素。与IPP-PADFE方法相比，MPD-BAE方法的改善较为明显，信噪比为16 dB时，BER减小了1个数量级，随着信噪比的提高，这种优势将扩大；与采样速率线性均衡方法相比，MPD-BAE方法在小信噪比条件下BER与其相当，因为没有训练序列，较大的噪声功率和脉冲间干扰影响了多脉冲检测器的检测性能，随着信噪比的提高，MPD-BAE方法的优势逐步显现。

在晴天轻度阴影衰落条件下，系统BER性能损失相对较小，三种方法对BER均有较大的改善，其中MPD-BAE方法性能最优。BER为10-5时，MPD-BAE方法所需信噪比较IPP-PADFE方法减少了2 dB，较采样率线性均衡方法减少了1 dB。

3 结束语

本文联合多脉冲检测的PSWF正交调制信号盲自适应均衡方法，利用多脉冲检测消除脉冲间干扰的能力降低均衡模块的阶数及算法难度，同时，利用均衡模块对信道的部分补偿作用为多脉冲检测改善信道环境，不需要发送训练序列。通过仿真分析，该方法优于判决反馈类均衡方法和采样速率线性均衡方法，但计算量仍然较高，以此换取恶劣信道条件下可靠性和传输效率的提高。下一步将对算法进行改进，进一步提升其性能。