具有访问约束和随机时延的网络化系统动态输出反馈控制
祝超群, 张 磐
(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业过程先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 电气与控制工程国家级实验教学示范中心, 甘肃 兰州 730050)
网络化控制系统(networked control system,NCS)是指通过通信网络将处在不同区域的控制器与传感器/执行器连接起来,构成对被控对象实现控制的闭环反馈控制系统[1-4].与采用点对点控制方式的传统控制系统相比,NCS具有成本低、布线少、易于扩展和维护、可靠性高以及便于远程操作等优点,使得NCS在工业、交通和电力等领域得到了广泛应用.当控制器与传感器/执行器通过通信网络交换数据时,由于通信网络带宽有限,在每个采样周期内只有部分传感器和执行器通过网络与远程控制器进行信息传输,这一现象叫做介质访问约束.由于控制系统具有实时性的特点,介质访问约束的存在使得传感器的量测信号和执行机构的控制信号不能及时得到更新,引起系统性能下降,甚至会导致系统失稳.为了解决这一问题,需要采用有效的通信调度策略来充分利用有限的带宽资源.
国内外学者针对访问约束问题作了大量的研究工作,并且取得了一些成果[5-7].Brockett[8]针对系统中存在的介质访问约束问题,首次提出了采用通信序列来描述网络介质的访问顺序,对具有访问约束的系统进行通信调度.Walsh等[9]基于反馈控制与实时调度理论,提出了一种静态与动态相结合的通信调度策略.Branicky等[10]在事先完成控制器设计的情况下设计通信调度策略,该方法不仅适合于静态调度策略,而且适合于动态调度策略,但被控对象的选取会受到一定的限制,得到的结果具有较大的保守性.Hristu-Varsakelis等[11]采用基于动态调度的通信策略序列,借助状态反馈信息在线确定传感器/控制器的介质访问序列,但他们只考虑了传感器端到控制器端的访问约束问题,忽略了控制器端到执行器端的介质访问约束现象.Guo和祝超群等[12-13]将具有介质访问约束的NCS建模为马尔可夫跳变系统,并在此基础上采用状态反馈的方法完成了控制器的设计.上述研究都只是单独考虑了通信网络的介质访问约束问题,但在实际的NCS中,数据丢包、信号量化、诱导时延和访问约束等网络诱导现象往往是并存的.孙连坤等[14]针对具有访问约束的NCS,研究了在随机通信调度策略下系统的稳定性问题,虽然控制器可以将系统状态收敛于一定区间内,但这并不是严格意义上的收敛.近年来,又有学者将网络中存在的介质访问约束处理为通信调度协议来解决这一问题,以避免网络传输过程中发生数据冲突.Zou等[15]研究了具有随机调度协议的线性时变系统的H∞故障估计问题,设计了相应的时变故障估计器.Zou等[16]研究了一类具有随机调度协议的线性时变系统的H∞控制问题,设计了相应的控制器,保证了闭环系统的鲁棒性能.Zou等[17]研究了具有随机通信协议的线性时变系统滤波问题,采用递推滤波算法使得滤波误差的协方差最小来获得满意的滤波效果.Wang等[18]研究了针对TOD协议复杂网络的滤波问题,最后设计了相应的H∞滤波器.
此外,由于网络负载的不规则变化,在NCS中不可避免地存在网络诱导时延,刘丽丽等[19-20]针对具有短时延的NCS控制问题进行了研究,将通信网络中的时变时延转变为系统矩阵的不确定参数,在此基础上进行系统稳定性分析,并设计了状态反馈控制器.Li等[21]研究了一类具有短时延和随机数据包丢失的H∞控制器设计问题,利用李亚普诺夫稳定性理论给出了使系统指数均方稳定的充分条件.Zhang等[22]研究了一类具有时变时延和随机丢包的H∞滤波器设计问题,但只对系统的输出进行了估计,并没有估计系统的状态.周颖等[23]研究了一类具有时变短时延的量化反馈鲁棒控制问题,给出了系统稳定性的充分条件和鲁棒控制器的设计方法.杜明莉等[24]针对一类同时具有访问介质约束和随机时延的NCS,提出了一种基于TOD动态通信调度与鲁棒H∞控制器的协同设计方法,采用状态反馈的方法得出了使系统具有H∞性能的控制律.
通过上述分析可知,目前关于访问约束的研究大多采用动态通信调度、静态通信调度和通信调度协议的方法,往往忽略了访问约束的随机特性.并且大多文献只单独考虑了通信网络中访问约束的问题,而很少考虑网络中的其他网络诱导因素,如网络时延、数据丢包和信号量化等.此外,大多数网络化系统控制综合都采用基于状态的控制方案,而在实际的系统控制中,系统状态很难通过直接测量获得.
基于上述存在的问题,本文针对同时具有随机时延和访问约束的NCS,研究系统的动态输出反馈控制问题.首先根据介质访问约束和随机时延特性将系统建模为具有参数不确定性的马尔可夫跳变系统;其次,基于李雅普诺夫稳定性理论和LMI技术给出系统稳定的充分条件,并设计了动态输出反馈控制器使得闭环系统鲁棒稳定,且具有给定H∞性能;最后,通过仿真算例验证所提出方法的正确性和有效性.
1 问题描述
考虑如图1所示的NCS,被控对象的连续时间系统模型为
(1)
其中:x(t)∈Rn,u(t)∈Rm,y(t)∈Rr,z(t)∈Rv和ω(t)∈Rq分别表示被控对象的状态、控制输入、输出、被调输出以及有限能量的外部扰动;A、B、C1、C2、H0、H1和H2是具有相应维数的常数矩阵.
1.1 网络时延

1) 传感器节点采用时间驱动,以周期T进行采样,控制器和执行器节点由事件驱动;

由以上假设可知,在一个采样周期中,执行器会输入两个不同的控制信号uk和uk-1,即
(2)
综合考虑式(1)和式(2),则被控对象的离散化状态空间模型为
(3)
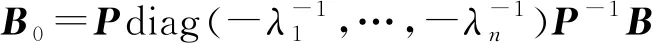
F(τk)=diag(eλ1(T-τk-c1),…,eλn(T-τk-cn))
E=P-1B
c1,…,cn的选择满足eλi(T-τk-ci)<1,i=1,…,n.
同理,可以证明
Bd1=B1-DF(τk)E
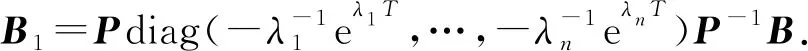
1.2 介质访问约束

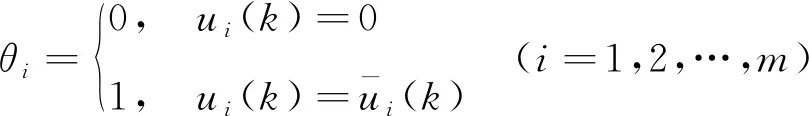
(4)

(5)
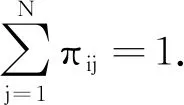
联立式(3)和式(5),可得具有随机时延和访问约束的网络化系统状态空间模型为
(6)
对网络化系统(6)设计动态输出反馈控制器为
(7)
其中:xc(k)∈Rp(p≤n)为控制器状态,当p=n时,对系统进行全阶动态补偿,当p 综合考虑到式(6)和式(7),可得 (8) 由于τk是小于一个采样周期的不确定性时延,Bd0(τk)、Bd1(τk)是随机矩阵,则离散化模型式(8)可等价为 (9) 其中:Q1=(B0+DF(τk)E)Mθ(k)Cc;Q2=(B1-DF(τk)E)Mθ(k-1)Cc;B0、B1、D、E都是常数矩阵;F(τk)随τk发生变化且满足FT(τk)F(τk)≤I. 可以看出,具有动态输出反馈控制的闭环网络化系统(9)是一个具有不确定参数的马尔可夫跳变系统. 本节的目的是设计使闭环系统(9)具有扰动衰减率为γ的H∞鲁棒稳定控制律.为了便于描述,在下文中将Mθ(k)和Mθ(k-1)简写为Mi和Mi-1.当ω(k)=0时,闭环系统(9)可写为 (10) 定义1当外部扰动ω(k)=0时,对于含有随机时延τk∈0T且满足FT(τk)F(τk)≤I的闭环系统(9),如果存在一个李雅普诺夫函数V(·)>0,且V(·)沿系统的前向差分ΔV(·)<0,则称闭环系统(9)是鲁棒稳定的. 为了便于后面的定理证明,先不加证明地给出以下引理. 引理2(S-procedure) 对于实矩阵W、M、N和F(k),其中W是对称的,则不等式 W+MF(k)N+NTFT(k)MT<0 对于任意满足FT(k)F(k)≤I的F(k)都成立,当且仅当存在标量ε>0,使得 W+εMMT+ε-1NNT<0 (11) 其中: N77=-ε1I,N88=-ε1I 则称闭环系统(9)是鲁棒稳定的. 证明定义李雅普诺夫函数: (12) 其中:P∈Rn×n,Z∈Rp×p和S∈Rp×p为对称正定矩阵.记Q1=(B0+DFE)MiCc,Q2=(B1-DFE)Mi-1Cc和F=Fτk,则有 ΔV(·)=xT(k+1)Px(k+1)+ 根据李雅普诺夫稳定性定理,当 (13) 时,该闭环系统稳定,则式(13)可以写成 (14) 对式(14)应用Schur补性质,可得 将Q1和Q2展开得 (15) 其中: 对式(15)应用S-procedure,当且仅当存在标量ε>0,使得 类似地,再次应用引理1和引理2,可得 (16) 其中: O44=εDDT-P-1,O55=-εI O66=-S-1 (17) 其中: Υ77=-ε1I,Υ88=-ε1I 当ω(k)≠0时,对闭环系统(9)进行稳定性分析,并设计抗扰动衰减率为γ的H∞鲁棒控制器. 定理3当系统外部扰动ω(k)≠0时,对于闭环系统(9),给定的衰减率γ>0,若存在对称正定矩阵P∈Rn×n,Z∈Rp×p,S∈Rp×p,标量λ1,使得以下矩阵不等式成立: (18) 其中: V77=-λ1I 则称闭环系统(9)为抗扰动衰减率γ的H∞鲁棒稳定. 证明设 (19) 考虑闭环系统(9),有 (20) 其中: 当需要ψ≤0时,只需φ<0即可,即有 (21) 式(21)可写为 (22) 其中: 对式(22)使用Schur补性质,可得 (23) 其中: 对式(23)采用与式(14)同样的处理方法,依次使用Schur补性质、S-procedure和Schur补性质可得 (24) 其中: U55=λ1DDT-P-1,U66=-S-1 U77=-λ1I 定理3得证. 定理4对于闭环系统(9),若存在对称正定矩阵P、S、Z,适当维数矩阵K1、K2、Y,标量λ1、λ2和ζ,使得以下矩阵不等式成立: <0 (25) 其中: Z66=-S, Ζ610=YT Ζ77=-λ1I,Ζ88=-I, Ζ99=-λ2I,Ζ1010=-λ2I 则称闭环系统(9)H∞鲁棒稳定,并且H∞扰动的衰减度为γ. 考虑如下参数的被控对象: 假设网络中存在随机时延τk∈0T,这里考虑在任意一个采样周期内执行器和控制器只有一个通信信道可以进行控制命令的传输,则访问介质序列集为 且有Mj,Mi∈W1W2,介质访问序列模态切换概率转移矩阵为 假设系统的初始状态为x0=4 -1T,采样周期为1 ms,根据定理1和定理2,利用LMI工具箱解得动态输出反馈控制律为 图2是通信网络中存在的随机时延;图3是执行器端介质访问序列的模态切换曲线,其中曲线值为1表明在该采样周期采用介质访问序列模态W1,曲线值为2表明采用介质访问序列模态W2,此时闭环系统(9)的状态轨迹如图4所示.由图4可以看出,在给定的初始条件下,同时具有访问约束和随机时延的闭环系统在动态输出反馈控制器的作用下,可保证随机稳定性,且具有良好的动态性能. 图2 随机时延 图3 介质访问序列切换模态 图4 无扰动下的状态轨迹图 在零初始条件下,即在x0=0 0T的情况下,加入如下的外部扰动: 图5给出的是ω(k)≠0时的介质访问序列切换模态曲线,此时系统状态轨迹如图6所示.从图6可以看出,在动态输出反馈控制器的作用下,闭环网络化系统(9)具有扰动衰减度γ的H∞性能. 图5 扰动情况下介质访问序列切换模态 图6 具有H∞性能的系统状态轨迹 为了说明本文设计方法的优越性,在同样的初始条件和外部扰动时,分别采用本文和文献[12]的控制方案进行仿真,对应的系统状态输出如图7和图8所示.表1给出了两种控制方案下系统的二次型性能指标.通过比较可以看出,本文的控制方案具有更加优越的控制性能. 图7 系统状态轨迹 图8 文献[12]状态轨迹 表1 二次型性能指标比较 当前大多数研究都是将介质访问约束和网络诱导时延问题独立起来进行研究,这与网络控制实践具有一定的差距.此外,大多数网络化系统控制综合都采用基于状态的控制方案,而在实际的系统控制中系统的输出信号更容易获得.因此,本文针对同时具有随机时延和介质访问约束的NCS,研究了系统的动态输出反馈控制设计问题.一方面,由于网络带宽有限,在每个采样周期内只有部分执行器通过网络与控制器进行通信,未能获得信道访问权的执行器输入被置为零值.另一方面,针对NCS中存在的随机时延,将其建模为系统矩阵的不确定性.结合上述两个方面,根据执行器和控制器之间访问约束的随机特性,将网络化系统建模为一类具有参数不确定性的马尔可夫跳变系统,进而基于李雅普诺夫稳定性理论和LMI方法导出使闭环系统稳定的充分条件,设计满足H∞扰动衰减度的动态输出反馈控制器,使得闭环网络化系统随机稳定并具有良好的鲁棒性能.2 主要结果

2.1 动态输出反馈控制器设计


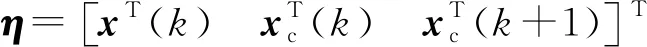



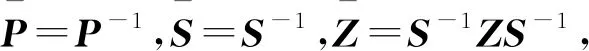

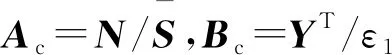

2.2 网络化系统控制系统H∞性能

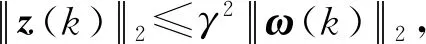


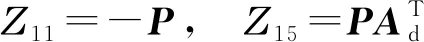
3 仿真实例
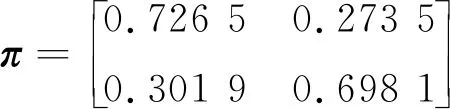



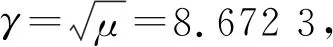


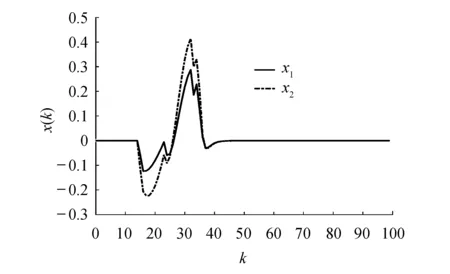
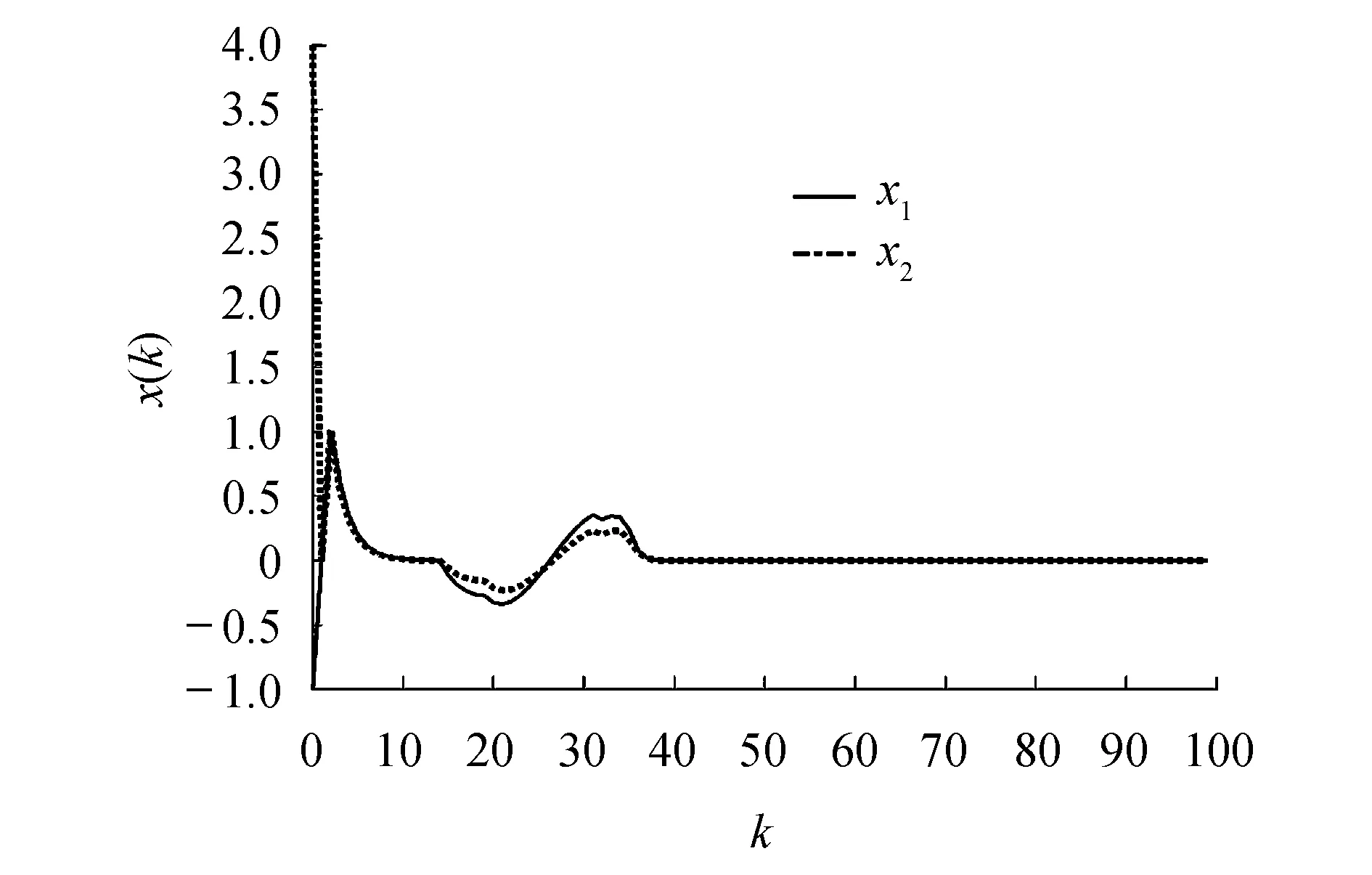
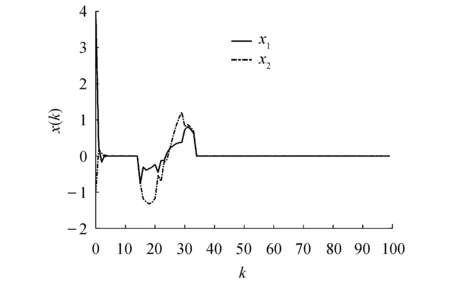

4 结论

