硫酸镁在硫酸溶液中的溶解度测定及关联

李永勇 金 鑫 李兴彬 魏 昶 彭晓华 江国豪 邓志敢

(昆明理工大学 冶金与能源工程学院，昆明 650093)

硫化锌精矿中通常含有0.3～0.5%的杂质镁，在硫酸浸出时以硫酸镁的形式与硫酸锌一同进入到浸出液。然而在整个湿法炼锌工艺过程中，硫酸镁不能被置换或者沉淀除去[1]，导致硫酸镁在湿法炼锌溶液中不断的循环累积，给工艺的顺行带来诸多危害[2-4]。导致溶液黏度增大、固液分离困难；硫酸镁容易在输送管道和设备内部结晶析出，堵塞管道；电解液中硫酸镁浓度增高导致溶液电阻增大，降低电流效率，增大电耗等问题。硫酸镁的危害已是湿法冶金过程中普遍存在而又长期未得到解决的行业难题。

根据魏昶、李兴彬等的研究[5]，在低温条件下，湿法炼锌废电解液中的硫酸镁、硫酸锌、硫酸等主要组元的溶解度及结晶行为差异变大，通过控制合适的工艺技术参数条件，可以采用结晶法脱除湿法炼锌废电解液中的大量硫酸镁。该方法具有无杂质离子引入、能耗低、无废水、废渣排放等优点，展现了良好的工业应用前景。然而，与湿法炼锌废电解液直接结晶除镁相关的固液相平衡及结晶热力学基础研究工作缺少文献资料报道，这制约了低温结晶除镁技术的发展。

硫酸镁在低温条件下的结晶析出是一个相平衡和相转移问题[6]，掌握硫酸镁在多金属复杂水盐体系中的溶解度及相平衡规律对于选择性结晶析出硫酸镁具有重要的指导意义。MgSO4-H2SO4-H2O三元系是湿法炼锌中的一个重要子体系。本文采用平衡法[7]测定了在温度263.15～298.15 K条件下，硫酸镁在硫酸水溶液中的溶解度数据，并分别用 Apelblat方程、多项式方程和(CNIBS)/Redlich-Kister方程对溶解度数据进行了关联，并回归了相关模型参数。所得数据将对掌握湿法炼锌过程硫酸镁的结晶行为规律，以及指导湿法炼锌废电解液结晶脱除硫酸镁新技术的研发提供数据支撑。

1 实验

1.1 试剂与仪器

实验用硫酸镁、氢氧化钠、硫酸、EDTA均为分析纯或基准试剂，去离子水为超纯制水机自制，电导率<5 μs/cm。低温恒温反应浴由上海保玲仪器设备有限公司生产；电子天平为梅特勒-托利多生产，精度为0.000 1 g；数显磁力搅拌水浴锅由金坛市盛威实验仪器厂生产。

1.2 实验方法

量取适量体积的硫酸水溶液置于恒温的夹套玻璃瓶中，并加入过量硫酸镁，恒温磁力搅拌，有固体剩余后静置。根据探索实验结果，静置4 h后的镁离子浓度相差不超过2%，可以认为已经达到平衡。为保证硫酸镁溶解能够充分达到固液平衡，本文采用的静置时间为6 h。用预热至稍高于平衡温度的移液管取上清液，采用EDTA滴定镁离子含量。硫酸水溶液的浓度用NaOH标液标定。据式1计算硫酸镁溶解度，每组至少测定3次，取平均值。

(1)

式1中，x为硫酸镁的摩尔分数，下同；M1、M2、M3为硫酸镁、硫酸和水的相对分子质量，g/mol；m1、m2、m3为硫酸镁、硫酸和水的质量，g。

1.3 可靠性实验

为了保证实验测定溶解度的方法的可靠性，首先测定了硫酸镁在水中的溶解度并与文献[8]进行了比较，结果见表1。其平均相对偏差为1.72%，因此，本文实验方法和装置测得的溶解度数据是可靠的。

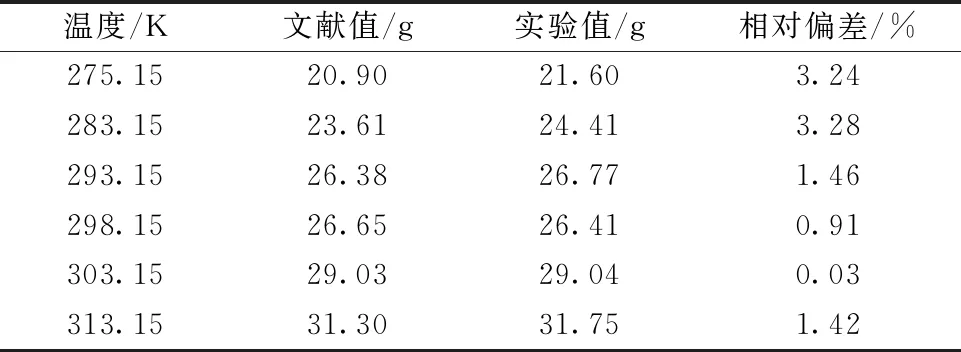
表1 硫酸镁在水中的溶解度Table 1 Experimental and calculated values of the solubility of magnesium sulfate in water

1.4 模型计算

固液相平衡数学模型中较为成熟的模型有活度系数法、状态方程法和经验模型法。其中状态方程法本是用于描述气液平衡的方程，在描述固液平衡状态时效果并不理想[9]。本文所测物系是电解质溶液，硫酸在水中存在二级电离现象，如式2、式3所示。

(2)

(3)

其中，一级电离为完全电离，二级电离为部分电离。由于溶液中的电离平衡及不同离子之间的结合平衡，使得离子种类较多，E-NRTL方程在应用于部分电离及容易发生缔合现象的电解质溶液时关联效果并不理想[10]。因此本文选用经验模型对实验数据进行关联。

1.4.1 Apelblat方程

Apelblat[11]方程参数不多，形式简洁，被广泛用于关联各种复杂电解质溶液中的溶质摩尔分数与平衡温度之间的关系：

(4)

式4中，a、b、c为方程参数。其中，a和b可表征溶液中活度系数的变化，c可以表征温度对溶解焓的影响[12]；T为绝对温度，K，下同。

1.4.2 经验方程

因为温度对溶解度的影响很大，本文采用式5的经验方程[13]回归溶解度数据。

x=A+BT+CT2

(5)

式5中，A、B、C为方程参数。

1.4.3 (CNIBS)/Redlich-Kister方程

(CNIBS)/Redlich-Kiste方程[14-16]适用于二元混合溶剂体系，可以用来拟合一定温度下溶解度与混合溶剂比例之间的关系，见式6。

(6)

式6中，B1、B2、B3、B4、B5为方程参数，xA为硫酸—水混合溶剂中硫酸的摩尔分数。

使用相对偏差(RD)和平均相对偏差(ARD)检测实验值和计算值的一致性，见式7、式8。

(7)

(8)

1.5 热力学性质

在理想溶液中，溶解度与熔化焓和熔化熵的关系可用Van′t-Hoof 方程表示。然而理想溶液是不存在的，对于真实物系，可用溶解焓替代熔化焓，以溶解熵替代熔化熵[17]，此时Van′t-Hoof方程如式9所示。

(9)

式9中，ΔHd为溶解焓，kJ/mol；ΔSd为溶解熵，J/(mol·K)；R为气体常数，J/(mol·K)。

溶解过程中的溶液吉布斯自由能变、溶解焓、溶解熵和平均温度的关系如式10、式11。

(10)

ΔGd=ΔHd-ΔSd·Tmean

(11)

式10和式11中的Tmean为平均温度，K。式11中的ΔGd为吉布斯自由能变，kJ/mol。

溶解焓和溶解熵为溶解过程中的驱动力，二者所占的比例分别用ξH，ξTS表示[18，19]，如式12、式13。

(12)

(13)

2 实验结果与讨论

2.1 硫酸镁的溶解度测定及关联

采用Origin软件对硫酸镁的溶解度实验数据进行拟合及参数回归，Apelblat方程、经验方程的拟合结果见图1和表2。可以看出，在0.5～3.0 mol/L的6个硫酸浓度条件下，温度由298.15 K降低至263.15 K时，硫酸镁的溶解度分别降低38.37%、41.79%、47.86%、50.98%、55.59%、59.83%，即降低温度可以使硫酸镁有效析出，且析出效率随硫酸浓度的升高而增大。低温下可以脱除硫酸水溶液中的硫酸镁且脱除效率随硫酸浓度的升高而增大。比较6个溶剂组成下所得48个数据点的实验值与计算值，可以发现，Apelblat方程的最大相对误差为1.63%，总平均相对误差为0.63%。经验方程最大相对误差为2.54%，总的平均相对误差为0.93%，两方程都显示了较好的关联结果。

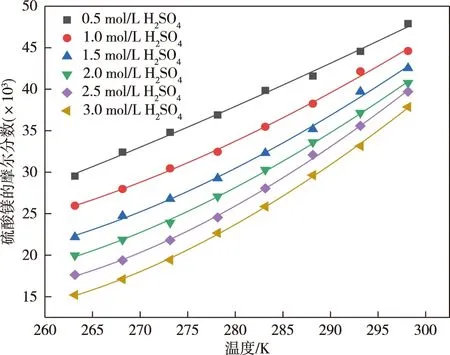
图1 硫酸镁在硫酸水溶液中的溶解度实验数据及Apelblat方程关联结果Fig.1 Experimental data and Apelblat equation correlation results of solubility of magnesium sulfate in sulfuric acid solution

Apelblat方程和经验方程模型参数回归结果见表3。

表3 Apelblat方程和经验方程模型参数回归结果 Table 3 Parameters of the Apelblat equation and empirical equation

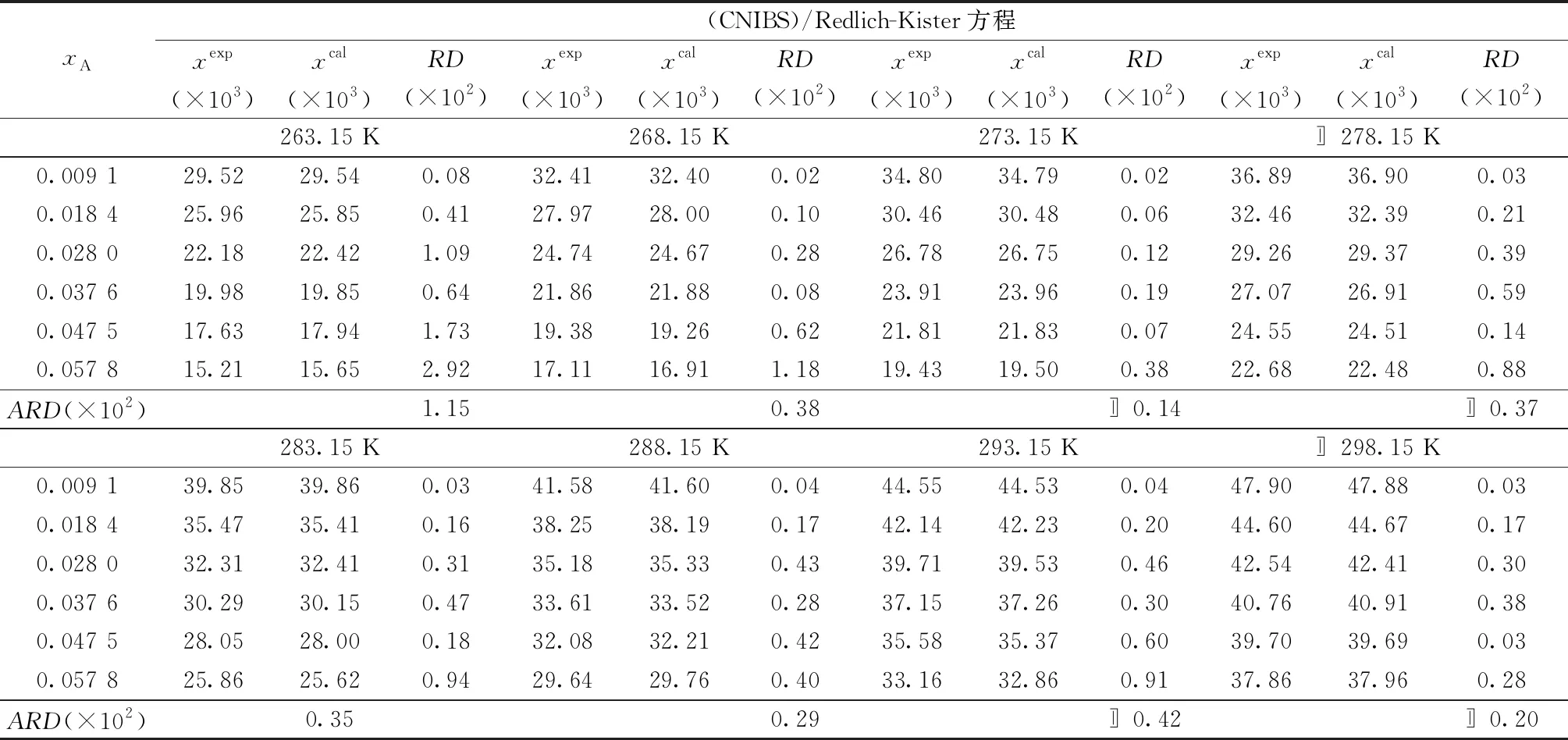
表4 硫酸镁溶解度数据及(CNIBS)/Redlich-Kister方程拟合偏差Table 4 Solubility data of magnesium sulfate and fitting deviation of(CNIBS)/Redlich-Kister equation

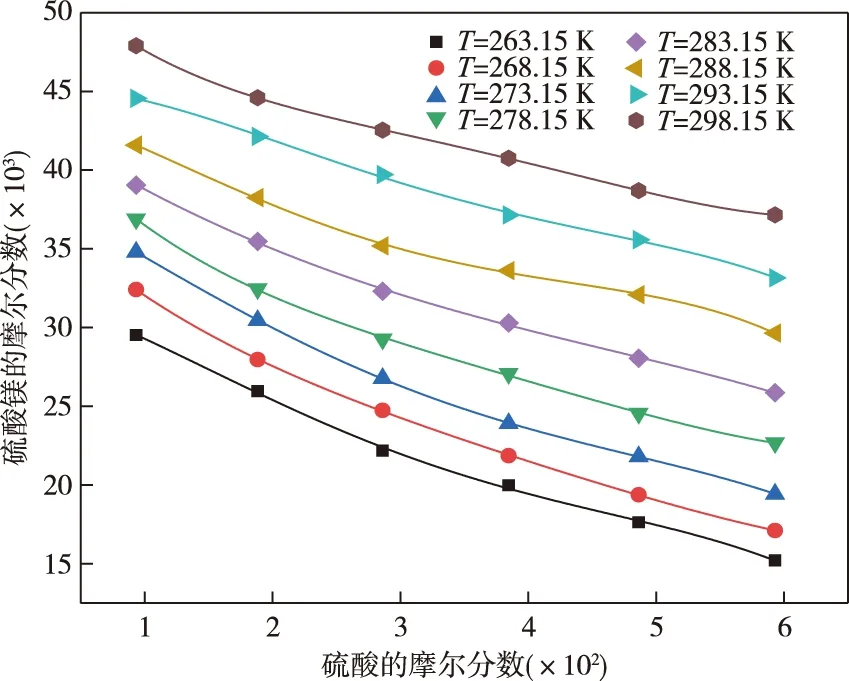
图2 硫酸镁在硫酸—水混合溶剂中的溶解度与溶剂组成的关系Fig.2 Relationships between solubility and solvent composition of magnesium sulfate in sulfuric acid-water mixed solvent

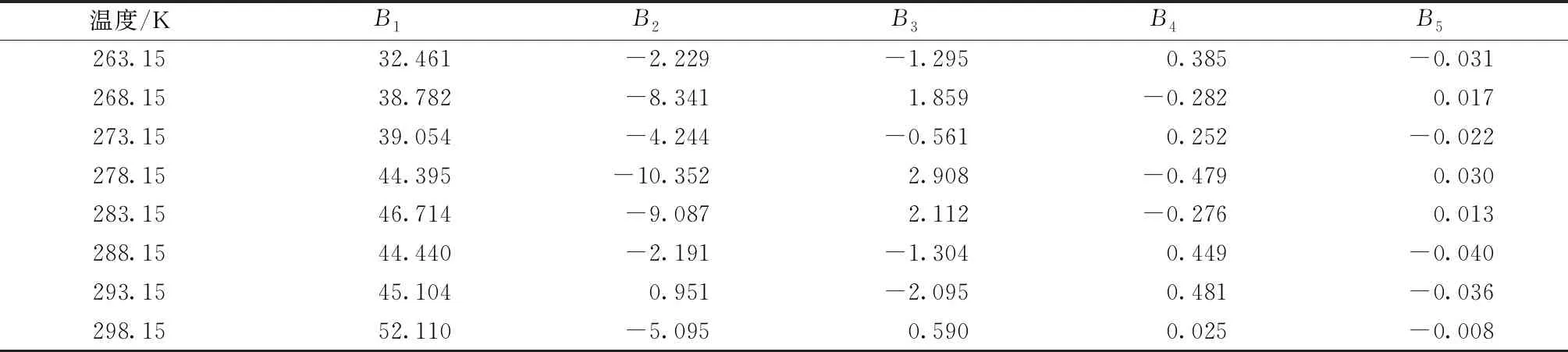
表5 (CNIBS)/Redlich-Kister方程模型参数回归结果Table 5 Parameters of the(CNIBS)/Redlich-Kister equation

2.2 硫酸镁溶解热力学性质

固液平衡体系的热力学性质可以通过修正的Van′t-Hoff方程来计算。根据热力学原理，在实验温度范围内，溶解熵和溶解焓可以视为常数，其值由式9可计算得到。根据式10计算得Tmean=282.56 K，由式11、式12、式13可计算得到吉布斯自由能变、焓驱动力占比(ξH)和熵驱动力占比(ξTS)。结果列于表6。

表6 硫酸镁溶解的热力学性质Table 6 Thermodynamic properties of dissolution of magnesium sulfate

由表6可知，溶解焓和溶解熵都大于0，说明溶解过程为吸热、熵增过程。溶解焓随硫酸浓度的升高而增大，这与表3中Apelblat方程参数c的趋势是一致的。因为参数c可以表征对溶解焓的影响，因此用Apelblat方程关联硫酸镁的溶解过程时参数c的值与溶解焓呈正相关。吉布斯自由能变小于0，溶解过程自发进行，ξH<ξTS，因此溶解过程为熵驱动。

3 结论

1)在263.15～298.15 K低温条件下降低温度可以使硫酸溶液中的硫酸镁析出。硫酸镁在0.5～3.0 mol/L硫酸溶液中的平衡溶解度随温度的降低或硫酸浓度的增大而减小。溶液温度由298.15 K降低至263.15 K时，硫酸镁的溶解度分别降低38.37%、41.79%、47.86%、50.98%、55.59%、59.83%。该结果数据可为湿法炼锌废电解液中的大量硫酸镁脱除提供参考。

2)Apelblat方程、经验方程和(CNIBS)/Redlich-Kister 方程对实验溶解度数据进行的关联结果相比较，计算值与实验值总的平均相对误差分别为0.63 %、0.93%和0.41%，(CNIBS)/Redlich-Kister 方程的关联效果最好。

3)修正的Van′t-Hoof方程的热力学计算结果表明，硫酸镁溶于硫酸水溶液过程为吸热、熵增、熵驱动的自发进行的过程。