新型地锚张弦梁式泥石流格栅坝构件受力的简化计算方法

王永胜，吕宝宏，王金珂，王 冰

（1. 兰州理工大学 土木工程学院，甘肃 兰州 730050；2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，甘肃 兰州 730050）

1 研究背景

我国是世界上泥石流分布最广、数量最多和危害最重的国家之一［1］。目前，工程防治结构是减轻泥石流灾害最有效的手段。早期的重力式拦挡坝建造材料为浆砌石，在泥石流冲击作用下变形小、强度低，易被摧毁［2-3］。1950年代以来澳地利、日本等国家研究人员提出了一系列在坝体上设置开口的透水坝［4-5］。汶川地震之后，针对地震扰动区高位泥石流能量大、破坏力强等特点［6］，学者们对传统实体坝和透水坝进行了结构优化与创新，相继推出了一些新型坝体。陈紫云等［7］提出了鱼嘴式穹隆格栅坝型泥石流水石分离结构，利用结构的空间形态，使结构主要受压，提高材料的利用率；王永胜等［8］提出了地锚扶壁式泥石流格栅坝，利用扶壁和地锚技术减轻泥石流对结构的冲击破坏，提高坝体的稳定性；苏洁等［9］提出了石笼拱柔性拦截坝新技术，利用拱形石笼和废旧轮胎防冲垫层有效提高了泥石流拦挡结构的抗冲击性能；王秀丽等［10］在传统格栅坝的基础上提出了一种新型钢结构空间网格拦挡体系，增强了结构的整体刚度和强度；王东坡等［11］将竖向拦挡坝结构优化为弧形拦挡坝，引导泥石流从动能向势能转换，提高了拦挡坝的抗冲击能力。

传统和新型拦挡坝设计时未充分考虑泥石流流速分布特征，均从增强防治结构本身的强度和刚度或改变防治结构空间形态的角度出发，提高防治结构的抗冲击性能，结构常处于被动受力状态，属于“硬抗”消能方式，会造成结构构件截面尺寸大，基础埋置深，经济浪费等问题。另外，坝体修建用料多且体积大，而山区工地现场受限严重，施工难度大，速度慢。为此，本文基于“柔性消能”理念，提出一种既能改善结构受力性能、增加结构整体抗冲击能力、保证结构安全可靠，又能减小结构构件截面尺寸、节约成本、便于现场施工组装和后期运营维护的新型地锚张弦梁式泥石流格栅坝。阐述了其技术原理，给出相应的简化设计计算方法。利用SAP2000 建立新结构有限元模型，分析结构的整体受力，验证构件简化计算方法的合理性，分析本文简化方法计算值和有限元计算值的误差。以期研究成果能为新结构的设计计算和推广应用提供理论依据和技术支持。

2 新型地锚张弦梁式泥石流格栅坝的提出及工作原理

2.1 结构的提出及构造针对传统拦挡坝被动受力、抗冲击性能差和经济效益低等问题，提出一种新型地锚张弦梁式泥石流格栅坝，如图1—3 所示［12］。新型地锚张弦梁式泥石流格栅坝由上部格栅和下部基础两部分构成。上部格栅由竖杆、张弦梁结构、牛腿和立柱组成。两根立柱上沿竖向设置有多个牛腿，张弦梁结构通过滑移支座与牛腿相连，且滑移支座在牛腿上只可沿与来流相垂直方向左右移动，多层张弦梁结构通过竖杆相连接。其中，张弦梁结构包括张拉索、张弦梁和撑杆，张拉索两端通过锚具连接于张弦梁，多根撑杆布置于张弦梁和张拉索之间。下部基础由立柱、基础梁和竖向预应力锚杆组成。基础梁上表面与地面平齐，且两端与立柱现浇，立柱向下延伸埋入土体充当基础，多根水平间隔设置的竖向预应力锚杆顶端锚固于基础梁内部。新型地锚张弦梁式泥石流格栅坝是“柔性消能”结构，适用于防治含有大块石的稀性泥石流和水石流。

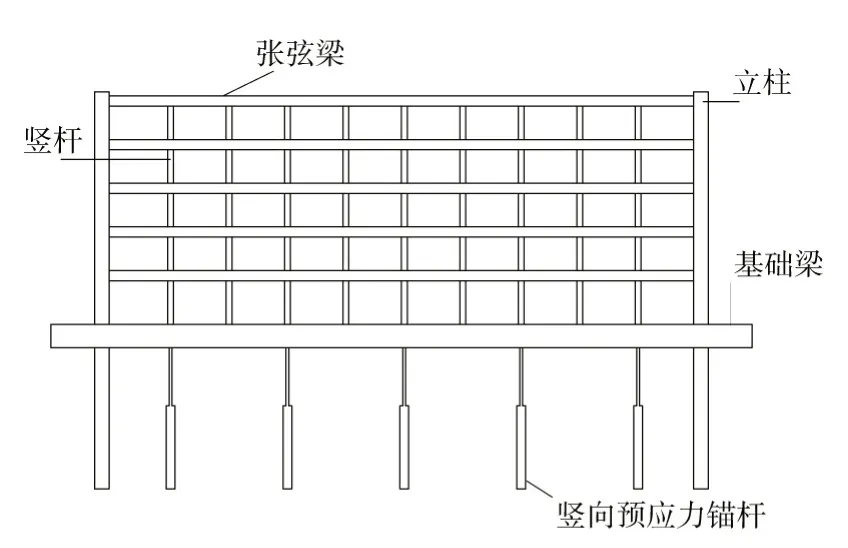
图1 地锚张弦梁式泥石流格栅坝正立面图

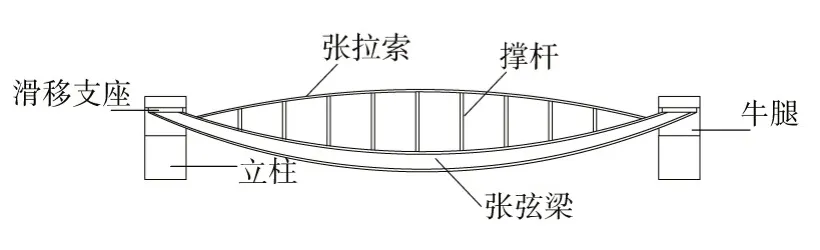
图2 张弦梁结构体系详图

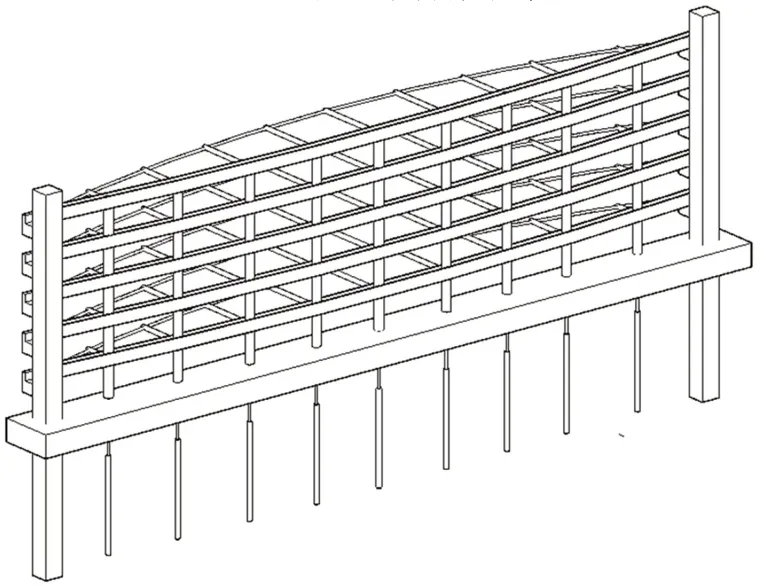
图3 地锚张弦梁式泥石流格栅坝三维图

2.2 工作原理新型地锚张弦梁式泥石流格栅坝是一种轻柔性防治结构体系，既能柔性消能，又能对泥石流进行拦挡疏通，其工作原理主要包括以下2 个方面。

（1）柔性消能。泥石流发生时，置于迎流面的张弦梁结构是主要的抗冲击力构件。当泥石流荷载作用于张弦梁上时，撑杆将泥石流荷载传递到张拉索使其绷紧，撑杆和张拉索作为弹性支撑，对张弦梁产生回拉，张弦梁对两端支座产生的水平推力由张拉索承受，改善了受力性能。泥石流冲击能量在张弦梁与张拉索的一张一拉间被消耗，实现了结构的柔性消能，减轻了结构的受力，保障了结构的安全。

（2）拦排结合。张弦梁与竖杆形成的格栅可以有效的拦蓄泥石流中的大部分较大固体物质，排走较小物质，达到水石分离，减少下泄泥石流的密度、流量和规模，降低下游遭受泥石流危害的程度。

3 新型地锚张弦梁式泥石流格栅坝的简化计算

3.1 荷载计算泥石流冲击破坏力主要由浆体动压力和大块石冲击力两部分组成。

3.1.1 浆体动压力 由文献［13］可知，浆体动压力为：

式中：Fδ为泥石流浆体动压力，kPa；γc为泥石流重度，kN/m3；Vc为泥石流流速，m/s；g 为重力加速度，g=9.8m/s2；α为防治结构受力面与泥石流冲压方向的夹角，（°）；λ为建筑物形状系数，圆形建筑物λ=1.0，矩形建筑物λ=1.33，方形建筑物λ=1.47。

3.1.2 大块石冲击力 由文献［14］可知，泥石流大块石冲击力为：

式中：R 为大块石半径，m；F 为大块石冲击力，kN。

3.2 结构简化设计方法新型地锚张弦梁式泥石流格栅坝由竖杆、张弦梁结构、牛腿和立柱组成，并与竖向预应力锚杆和基础梁连接形成一个整体，共同承受泥石流冲击作用。竖杆与张弦梁通过螺栓连接，其主要作用是竖向约束张弦梁，防止其发生侧向失稳破坏，其他约束作用较小；张弦梁与牛腿通过滑移支座连接，牛腿的主要作用是承受张弦梁沿泥石流方向的支反力；立柱和底层竖杆固接于基础。因此，新结构的构造连接方式主要为铰接，传力作用明显而对各构件变形约束较弱。结构变形仅对底层张弦梁和竖杆受力有影响，其它构件较小。故为工程应用方便，结构设计时，对其进行合理的简化，分解为竖杆、张弦梁结构、牛腿、立柱、竖向预应力锚杆和基础梁分别进行计算。立柱、竖杆和张弦梁组成的迎流面格栅直接承受并分配泥石流荷载。迎流面格栅构件均承受泥石流浆体荷载，而大块石为随机荷载，需综合考虑各构件的尺寸和泥石流浆体荷载的空间分布特征，对迎流面格栅构件布置相应集中荷载。受力分析时只需按竖杆-张弦梁-牛腿-立柱-基础的传递路径来计算间接荷载和相应构件直接承受的荷载。

3.2.1 竖杆计算

（1）内力计算。底层竖杆底端现浇于基础梁内，顶端通过螺栓与张弦梁连接，故将底层竖杆简化为一端固接，另一端铰接的梁；其他层竖杆均通过螺栓与张弦梁连接，简化为简支梁，如图4 和图5所示。

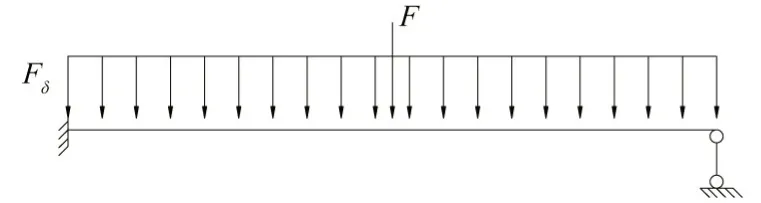
图4 底层竖杆间计算简图

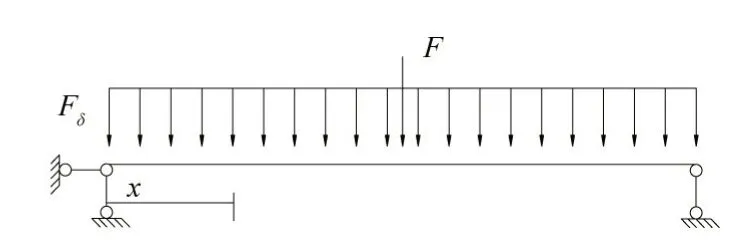
图5 其他层竖杆计算简图

底层竖杆属于一次超静定结构，将右端铰支座竖向反力视为多余力X1，取基本体系为悬臂梁，其基本方程为：

式中：δ11为基本结构在X1处施加单位荷载后沿X1方向产生的位移；Δ1P为基本结构在荷载单独作用下沿X1方向产生的位移；、分别为基本结构在单位荷载作用下任一截面弯矩（kN•m）和剪力（kN）；E 为竖杆的弹性模量， N•mm-2；I 为竖杆转动惯量，cm4。

由基本方程求出多余未知力X1后，利用叠加原理便可求出原结构内力。其他层竖杆为静定结构，其内力为：

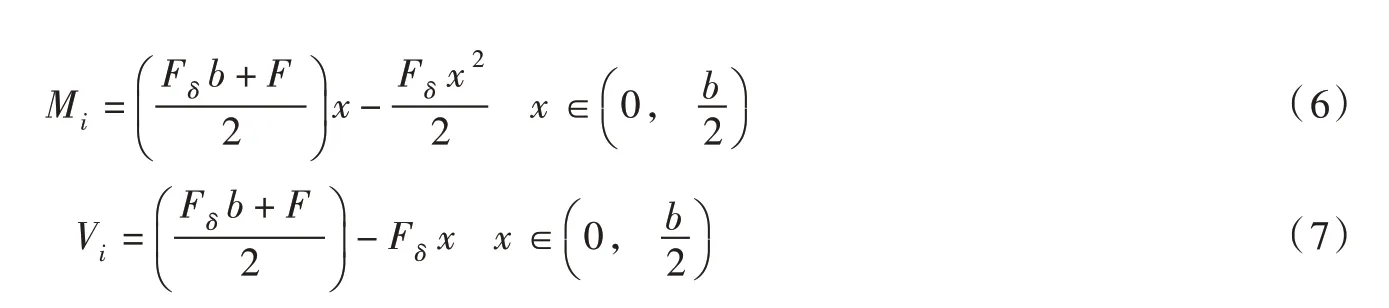
式中：b 为竖杆长度，m； x 为竖杆任意截面距左端支座的距离，m。

（2）截面设计。求得内力Mi和Vi后，根据规范要求［15］，验算竖杆抗弯强度和抗剪强度是否满足要求。

3.2.2 张弦梁结构计算

（1）内力计算。张弦梁结构内力由两部分组成，一部分由初始张拉时预应力产生，另一部分由泥石流荷载产生。将两部分内力线性叠加，可得结构的内力。

①初始张拉阶段内力求解。由文献［16］可知，本文认为施加的预应力应抵消泥石流浆体荷载产生的弯矩，即

式中：T1为施加的预应力，kN；l 为张弦梁结构跨度，m； f10和 f20分别为张弦梁的矢高和张拉索的垂度，如图6 所示。

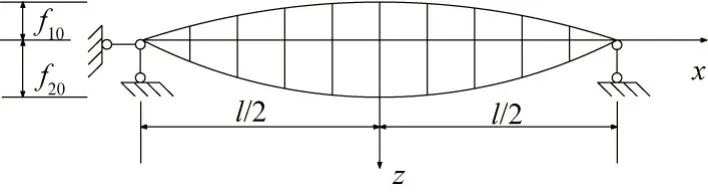
图6 张弦梁结构几何图

初始张拉时张弦梁结构受力如图7 所示，张弦梁内力为：

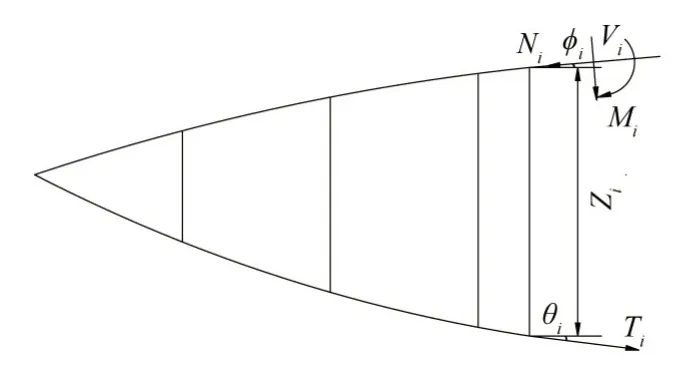
图7 初始张拉阶段张弦梁结构计算简图

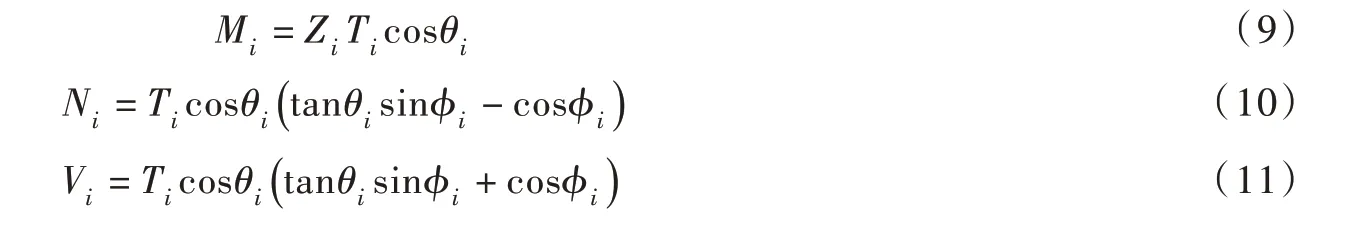
式中：Mi、Ni和Vi和分别为结构任一截面弯矩（kN•m）、轴力（kN）和剪力（kN）；θi、φi为张拉索和张弦梁在第i 个撑杆节点处与水平方向的夹角，（°），可通过曲线方程求得；Zi为第i 个撑杆高度， m；Ti为张拉索索段张力，kN，可由式（12）求得。

张拉索索段张力分布特点如图8 所示，由文献［17］可知，若任意相邻张拉索索段的张力分别为Ti和Ti+1，根据张拉索节点在撑杆轴线方向的平衡条件可知：

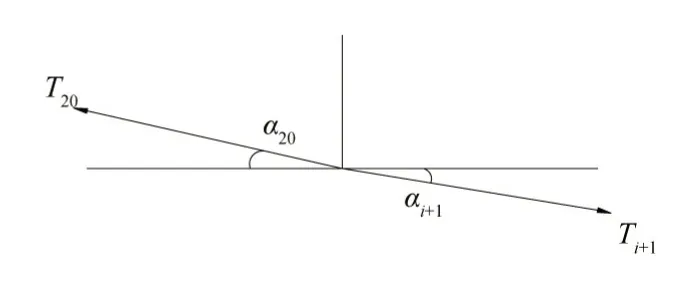
图8 张拉索索段张力示意

式中：αi和αi+1分别为撑杆左右相邻张拉索索段与水平方向的夹角，可通过张弦梁结构曲线方程（13）和（14）曲率求得。

张弦梁结构曲线方程为：

式中： z10、 z20分别为张弦梁和张拉索任意截面的竖向位置。

②泥石流荷载作用下张弦梁结构内力求解。泥石流荷载作用下张弦梁内力由两部分组成，一部分由荷载作用下张拉索索段张力产生；一部分由荷载本身产生。

荷载作用下张拉索索段张力对张弦梁产生的内力：

忽略撑杆作用和张拉索抗弯刚度，将张弦梁结构简化为一次超静定的两铰拱，如图9 所示。

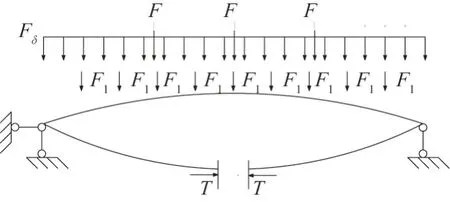
图9 荷载作用下张拉索索段张力计算简图

张弦梁结构基本方程为：

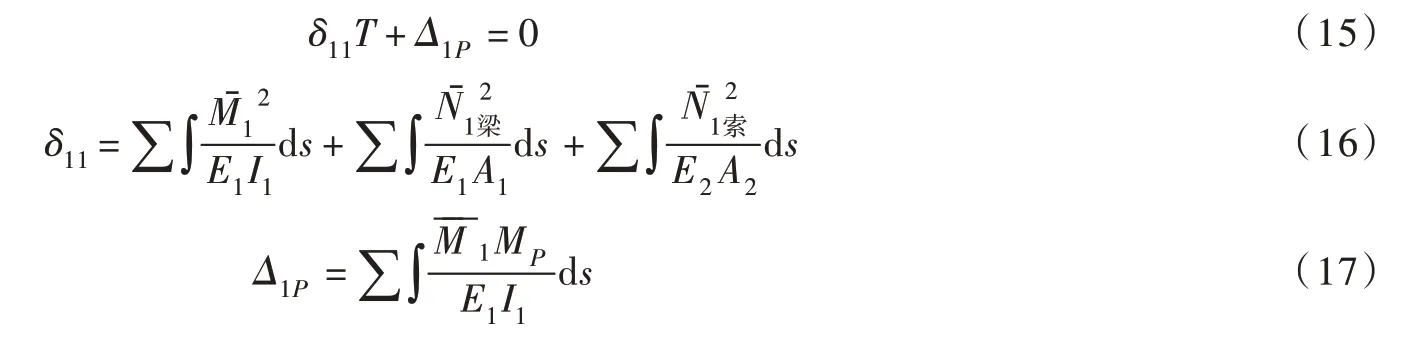
式中：E1为张弦梁弹性模量，N•mm-2，I1为张弦梁转动惯量，cm4；T 为张拉索跨中索段张力，kN；A1为张弦梁截面面积，cm2；E2为张拉索弹性模量，N•mm-2；A2张拉索截面面积，cm2；F1为竖杆传递到张弦梁上的集中力，kN。

求出泥石流作用下张拉索跨中索段张力T 后，将其代入式（9）—（11），可求出荷载作用下张拉索索段张力对张弦梁产生的内力。

荷载本身对张弦梁产生的内力：

将撑杆简化为弹性支座，刚度由撑杆相邻张拉索索段抗弯刚度提供，进而将张弦梁结构简化为多次超静定结构，如图10 所示。

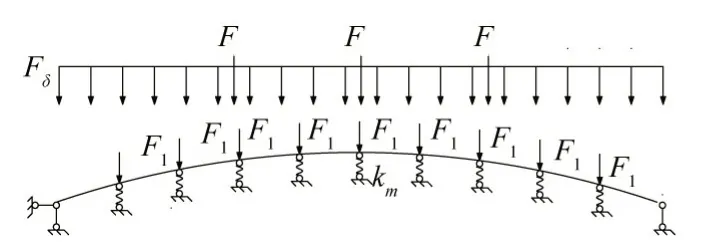
图10 荷载作用下张弦梁结构计算简图

简化后的张弦梁结构计算简图为多次超静定结构，取弹簧支座处释放的力矩Xi为多余未知力。按力法进行内力求解，其基本方程为：

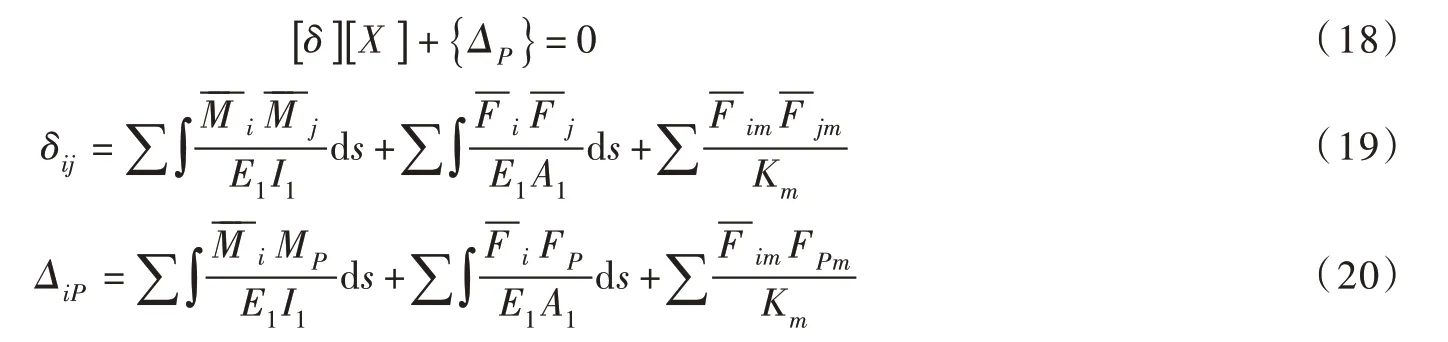
式中：δij为单位力Xj=1 产生的沿Xi方向的位移；为基本结构由于Xi=1作用而产生的内力； Km为第m 个弹性支座的刚度，N/m，可由式（21）和式（22）求得；为基本结构在第i 点施加单位弯矩后在第m 个弹性支座处形成的支座力，kN；FPm为基本结构在泥石流荷载作用下第m 个弹性支座处形成的支座力，kN。

由基本方程求出多余未知力Xi后，利用叠加原理便可求出原结构内力。相邻张拉索索段长度相差不大，可近似认为各弹性支座的刚度Km相同，如图11 所示。由文献［18］可知，张拉索抗弯刚度为：

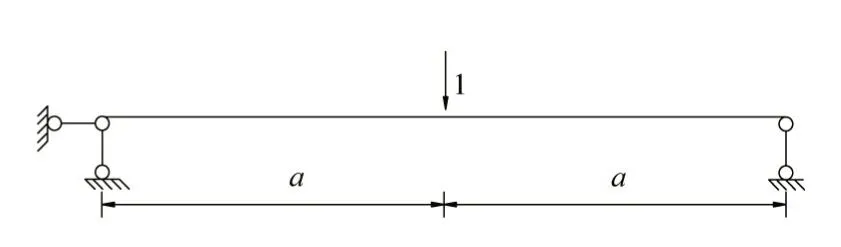
图11 弹性支座刚度计算简图

故弹性支座的刚度为：

式中：a 为撑杆水平间距； f12为张拉索第1 阶固有频率的理论值，Hz； fn2为张拉索第n 阶固有频率的理论值，Hz；a1、b1分别为第1 阶和第2 阶频率对应的常数；an、bn为第n 阶频率对应的常数；m为张拉索每米的重量， kg/m 。

（2）截面设计。求得内力Mi、Ni和Vi后，根据规范要求［15］，验算张弦梁抗弯强度和抗剪强度是否满足要求。

3.2.3 立柱和牛腿计算

（1）内力计算。①牛腿。牛腿为异形牛腿，将其分为R 部和U 部，分别进行内力计算，如图12所示。

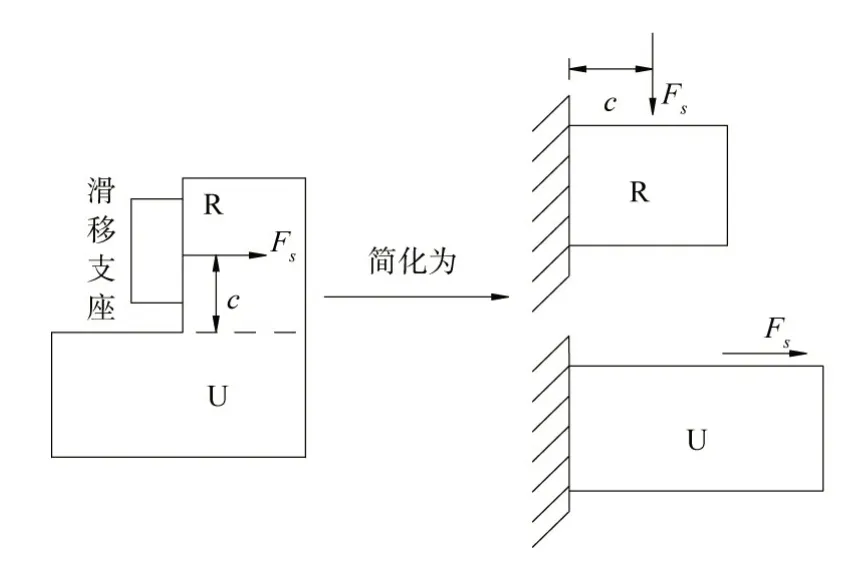
图12 牛腿计算简图

R 部：

U 部：

式中：Fs为张弦梁结构支座力，kN；c 为滑移支座中心距离U 部的距离， m 。

②立柱。根据立柱约束条件将其简化为悬臂梁，悬臂梁底端为立柱与基础梁的交界面，如图13所示。求解立柱内力时，应考虑大块石冲击力F 的作用位置和数量。

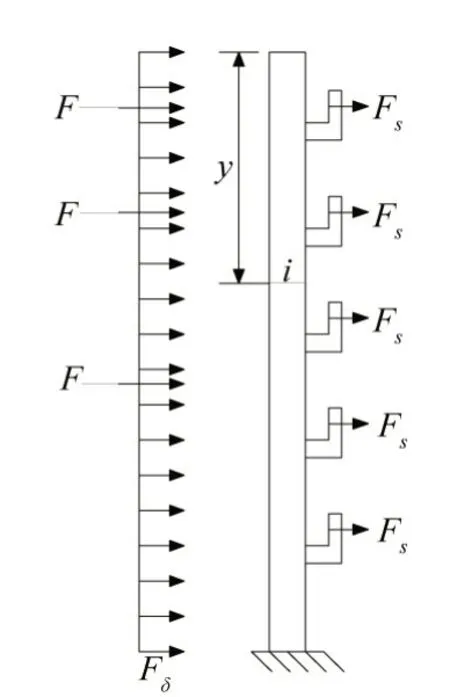
图13 立柱计算简图

式中：yi为第i 截面距立柱顶点的距离， m；n 为第i 截面以上F 和Fs的个数。

③立柱埋深。立柱埋深如图14 所示，由式（26）—（27）可求得立柱与地面相交处截面剪力Vi和弯矩Mi。根据静力平衡可得：

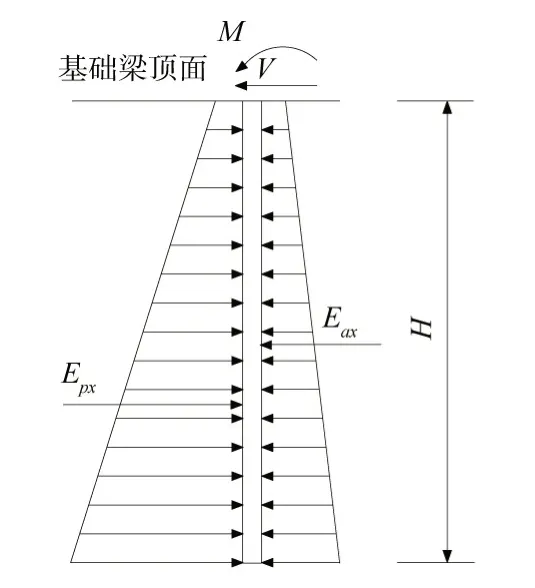
图14 立柱埋深计算简图

式中：Vi为立柱与基础梁交界面处剪力，kN ；Epx为立柱埋入段被动土压力，kN ；Eax为立柱埋入段主动土压力，kN 。

（2）截面设计。求得内力Mi和Vi后，根据规范要求［19］，按正截面受弯承载力和斜截面受剪承载力分别选配牛腿和立柱的受力纵筋和箍筋。

3.2.4 竖向预应力锚杆计算

（1）内力计算。竖向预应力锚杆受力如图15 所示。对于锚固在完整硬质基岩中的锚杆，因岩层的强度一般大于砂浆的强度，即岩层与孔壁砂浆的摩阻力一般大于砂浆对锚杆的握裹应力，抗拔力取决于砂浆对锚杆的平均握裹应力。

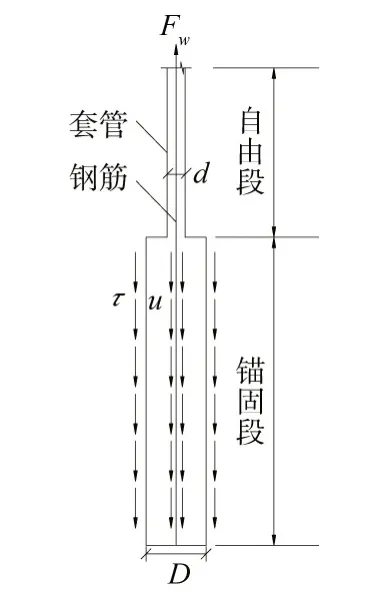
图15 竖向预应力锚杆计算简图

式中：Fw为锚杆的极限抗拔力，kN；d 为锚杆直径，m；Le为锚固段长度，m；u 砂浆对于钢筋的平均握裹应力， kPa 。

而对于锚固在风化岩层和土层中的锚杆，孔壁对砂浆的摩阻力一般低于砂浆对锚杆的平均握裹应力，抗拔力取决于锚固段周边砂浆与孔壁的平均抗剪强度。

式中：D 为锚杆钻孔直径，m；τ为锚固段周边砂浆与孔壁的平均抗剪强度，kPa。

（2）截面设计。求得抗拔力Fw后，按规范［20］要求，计算预应力锚杆截面面积、锚固段长度和自由段长度。

3.2.5 基础梁计算

（1）内力计算。基础梁与立柱现浇，故将其简化为两端固接的三次超静定梁，如图16 所示。Fl为竖向预应力锚杆施加的预应力。

图16 基础梁计算简图

将右端支座取掉，取基本结构为悬臂梁，则基础梁基本方程为：

式中： E3为基础梁弹性模量， N•mm-2；I3为基础梁转动惯量，cm4。

由基本方程求出多余未知力Xi后，利用叠加原理便可求出基础梁内力。

（2）局部受压承载力计算

式中： βc为混凝土强度影响系数， βl为混凝土局部受压时的强度提高系数， fc为混凝土轴心抗压强度设计值， N•mm-2； Aln为混凝土局部受压净面积， mm2。

（3）截面设计。求得内力Mi、Ni和Vi后，根据规范要求［19］，按正截面受弯承载力，斜截面受剪承载力和局部受压承载力计算分别选配基础梁的受力纵筋和箍筋。

4 工程算例

4.1 工程概况某泥石流沟，100年一遇泥石流容重1.53 g·cm-3，泥石流峰值流量为58.7 m3·s-1，一次泥石流总量为31 100 m3，一次固体物质总量为12 700 m3，沟床宽10 m，沟床上部为泥石流堆积物的块石土，呈稍密状，该层厚约3 ~ 10 m，下部为石英砂岩，块石土和砂岩为持力层，岩土参数，见表1。

表1 岩土参数

4.2 设计计算及结果分析

（1）初设参数选取。拟建新型地锚张弦梁式泥石流格栅坝跨度为10 m，高度6 m，竖杆水平间距1000 mm，竖杆长800 mm，外径300 mm，厚度取10 mm，立柱截面选用800 mm×800 mm，牛腿宽800 mm，厚400 mm，基础梁截面宽1000 mm、高1500 mm，设置4 根竖向预应力锚杆，水平间距为2.5 m。混凝土采用C35，钢筋采用HRB400 级钢筋，钢材选用Q235，张弦梁结构矢高和垂度均取1 m，张弦梁选用I56c号钢，张拉索采用高强预应力钢丝束∅5×301，撑杆9根，外径150 mm，厚度取6 mm。

（2）计算软件开发及应用。为方便新型地锚张弦梁式泥石流格栅坝的工程应用，基于结构内力计算理论，利用Python 语言和Qt Designer 软件，开发了界面友好、操作简单和实用的设计计算软件。

①计算软件主界面和具体模块如图17 和图18 所示。

图17 计算软件主界面

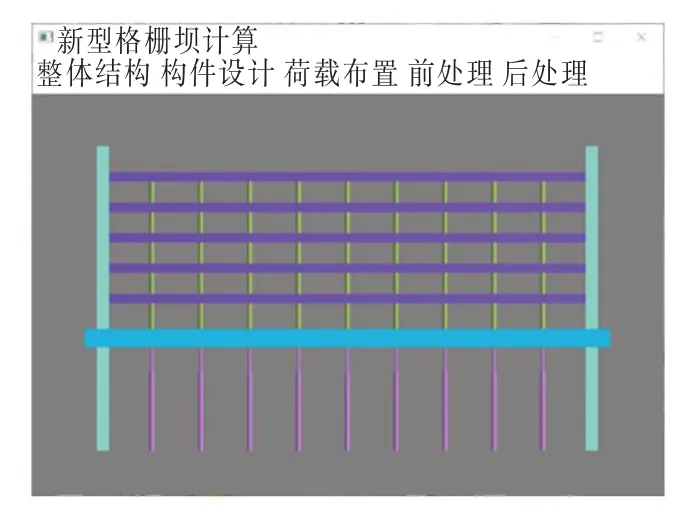
图18 计算软件具体模块界面

②输入参数为泥石流荷载，如图19 所示。结果输出为构件的内力，如图20 所示。

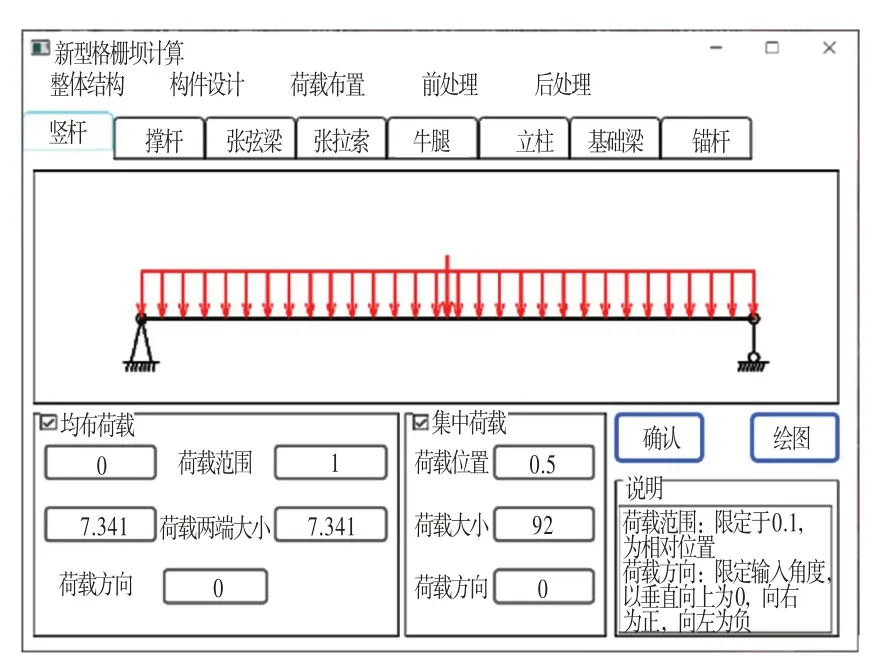
图19 计算软件数据输入界面

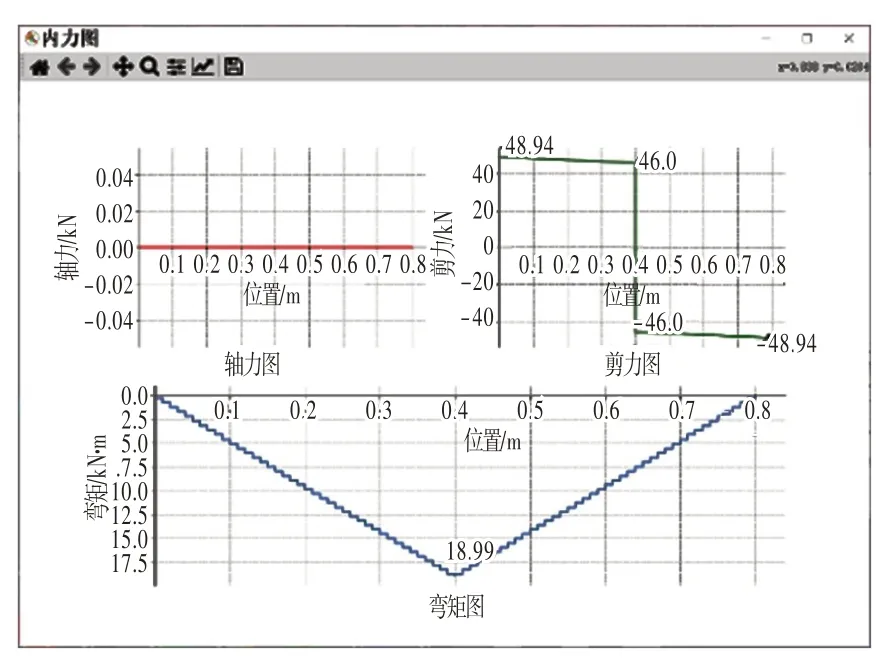
图20 计算软件结果输出界面

（3）结果分析。

①荷载计算。由式（1）和式（2）求得泥石流冲击力，结果见表2。

表2 泥石流冲击力

②竖杆验算。竖杆较短，假设只承受一个大块石冲击力，浆体动压力满跨分布。利用软件求得其最不利内力，并验算强度，结果见表3。

表3 竖杆验算结果

③张弦梁结构验算。根据泥石流流速分布特点，假设张弦梁结构在跨中和跨中左右各2 m 处承受大块石冲击力。由式（21）和式（22）求得张拉索抗弯刚度，利用软件求得初始张拉阶段和施加荷载阶段张弦梁的最不利内力，结果见表4。

表4 张弦梁结构内力计算结果

由表4 可得，张拉索轴向最大拉应力为193.5 kN，小于其强度设计值1110 MPa。求得张弦梁最不利内力后，验算其强度，结果见表5。

表5 张弦梁验算结果

④牛腿和立柱设计。利用软件求得牛腿R 部与U 部的内力，并计算其截面配筋，结果见表6。

表6 牛腿设计结果

假设立柱在1/4 和1/2 处承受大块石冲击力，利用软件求得立柱最不利内力和埋深，并计算配筋，结果见表7。

表7 立柱设计结果

⑤竖向预应力锚杆设计。泥石流荷载竖向分力远远小于预应力，故竖向预应力锚杆抗拔力满足预应力即可。预应力取锚杆钢筋屈服强度标准值的50%，利用式（30）求得竖向预应力锚杆抗拔力，并根据规范［20］求得其截面尺寸，结果见表8。

表8 竖向预应力锚杆设计结果

⑥基础梁设计。利用软件求得基础梁内力，并计算配筋，结果见表9。

表9 基础梁设计结果

由表3 可知，竖杆正应力为7.8 N/mm2远小于切应力75 N/mm2，这表明竖杆易发生剪切脆性破坏。由表5 可知，在直径1.7 m 的大块石作用下张弦梁最大正应力和剪应力分别为89.66 N/mm2和18.22 N/mm2，均小于相应的强度设计值。这表明将张弦梁结构应用于泥石流拦挡坝中，可以提高防治结构的抗冲击性能，保障结构的安全。由表7 可知，立柱内力最大，弯矩和剪力分别为2849.5 kN•m 和924.09 kN。立柱作为新型地锚张弦梁式泥石流格栅坝最重要的受力构件，破坏将危及整个结构的安全，后果严重。以后工程应用中可借鉴抗震设计中的“强柱弱梁”概念，考虑承载力储备，保证结构的安全性。

4.3 有限元模拟验证

4.3.1 构件简化计算合理性验证 为更直观的了解新结构各构件间的相互作用和荷载分配传递规律，模拟结构在泥石流荷载作用下的整体受力，采用SAP2000 软件建立了新型地锚张弦梁式泥石流格栅坝有限元模型（见图21）。新结构有限元模型由空间梁单元和索单元组成，二者均可在Frame Element 模块中实现。构件采用框架截面和索截面，并根据算例中的截面尺寸进行参数定义。新结构立柱和底层竖杆与基础梁现浇，故将二者与基础的连接定义为固定支座；竖杆和张弦梁螺栓连接，张弦梁两端通过滑移支座与牛腿连接，撑杆通过销轴节点和索球节点分别与张弦梁和张拉索连接。将竖杆与张弦梁、张弦梁与牛腿、撑杆与张弦梁和张拉索的连接定义为铰接，并对端部进行扭矩和弯矩（T、M2和M3）的释放处理。新结构的变形协调突出表现在各榀张弦梁和各层竖杆间，故仅提取张弦梁和竖杆的内力（见图22—25），即可分析新结构在泥石流作用下的整体受力。对第5 层竖杆施加泥石流浆体荷载，提取张弦梁与撑杆交界面处的内力，绘制每榀张弦梁内力曲线；每根竖杆只提取内力最大值，按结构跨度方向绘制每层9 根竖杆内力曲线。

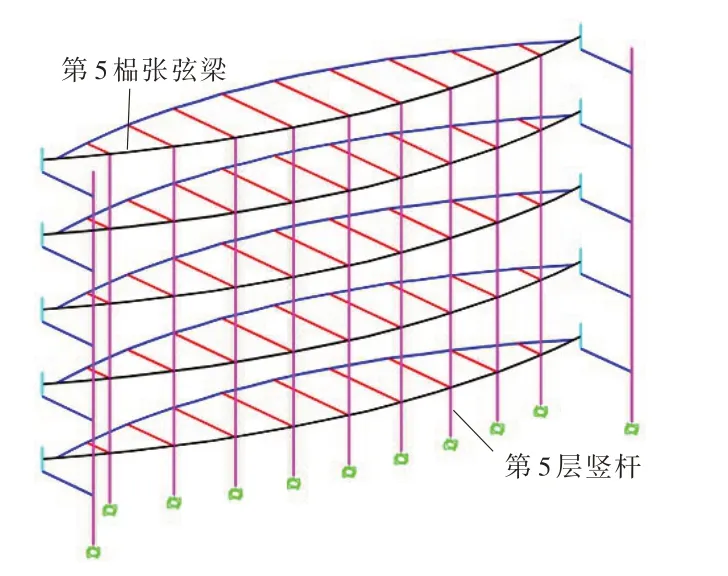
图21 新型地锚张弦梁式泥石流格栅坝有限元模型

由图22—24 可知，第5 榀和第4 榀张弦梁受力基本一致，张弦梁轴力、剪力和弯矩最值分别为-199.5 kN、-106.78 kN 和85.67 kN·m，第2 榀和第3 榀最值分别为8.29 kN、2.14 kN 和0 kN·m，远小于第4 榀和第5 榀，而第1 榀张弦梁最值为47.96 kN、34.27 kN 和-22.53 kN·m。可见张弦梁受力相互影响较弱，底层竖杆与基础的固接，导致变形协调仅对第1 榀张弦梁受力有一定影响。

由图25 可知，荷载作用下，仅第5 层和第1 层竖杆产生内力，第5 层竖杆弯矩和剪力最值分别为-18 kN·m 和60 kN，第1 层竖杆为20.17 kN·m 和25.21 kN。这表明变形协调对底层竖杆受力影响较大，对相邻竖杆受力无影响。

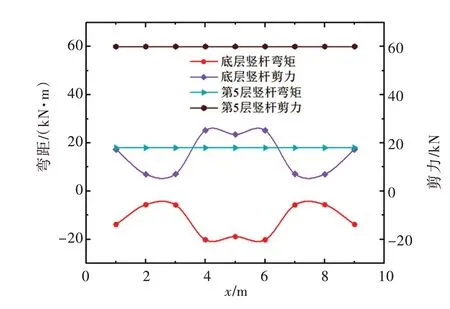
图25 竖杆内力

综上，可见变形协调仅对底层张弦梁和竖杆受力有一定影响，其余构件间受力相互影响较弱。因此，理论分析时将新结构简化为竖杆、张弦梁结构、牛腿、立柱、竖向预应力锚杆和基础梁分别计算是比较合理的。

4.3.2 本文简化计算方法的验证 为验证本文构件简化计算方法的正确性，基于工程算例，将各构件的简化方法计算值与有限元计算值进行对比分析，见图26—30 和表10。

由图26 可知，2—5 层竖杆弯矩有限元计算值与本文简化方法计算值基本一致，相差很小。底层竖杆弯矩和剪力最值分别为-142.91 kN·m 和227.57 kN，均比简化方法计算值大。因此新结构在设计计算时，应注意变形协调对底层竖杆内力的放大作用。由图27—29 可知，2—5 榀张弦梁内力变化趋势基本一致，其轴力、剪力和弯矩最值分别为539.01 kN、179 kN 和-167.88 kN·m，与简化方法计算值的误差分别为14%、23%和4.5%。第1 榀张弦梁内力与其它榀差异较大，轴力和剪力分别为65.31 kN和112.11 kN，均小于简化方法计算值；但弯矩为-277.1 kN·m，大于简化方法计算值。主要原因是变形协调导致第1 榀张弦梁受拉，产生负弯矩，而预应力也使之产生负弯矩，二者叠加使第1 榀张弦梁弯矩大于其它榀。由图30 可知张拉索最大拉力为564.49 kN，与简化方法计算值误差为23%。由表10可知牛腿的剪力和弯矩本文简化方法计算值与有限元计算值之间的误差为5.4%和5.1%；立柱的误差为7%和6.7%。

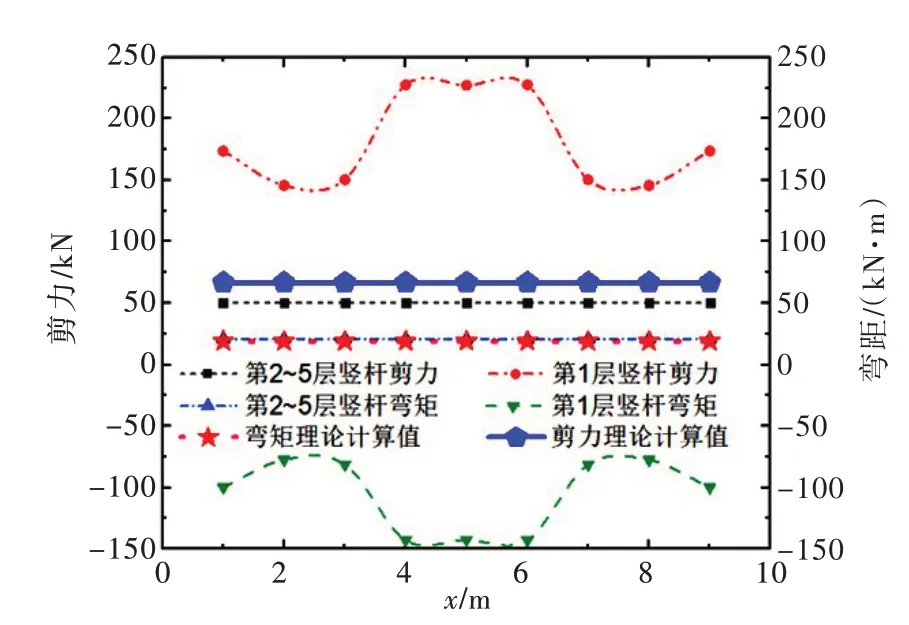
图26 竖杆内力

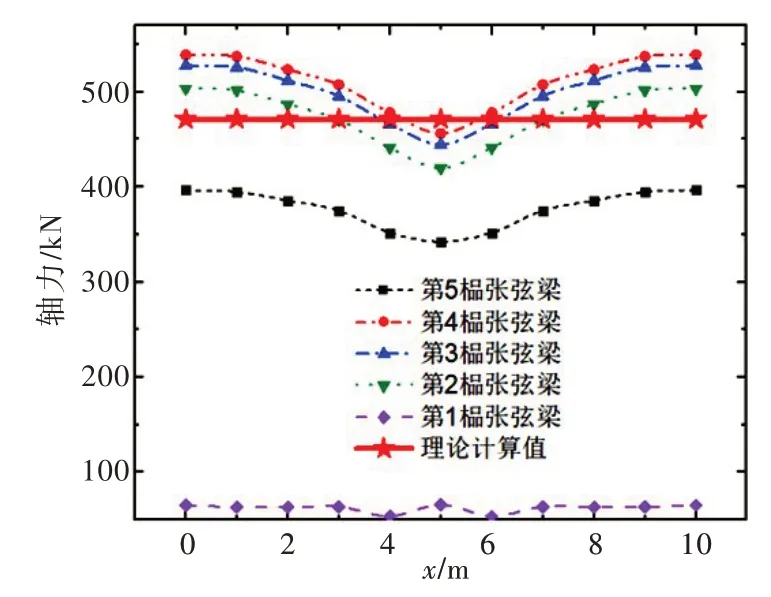
图27 张弦梁轴力

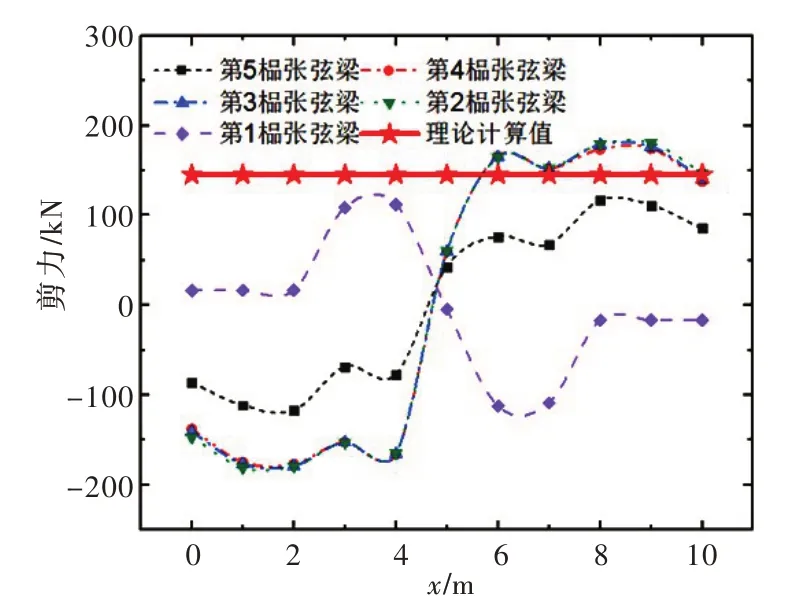
图28 张弦梁剪力

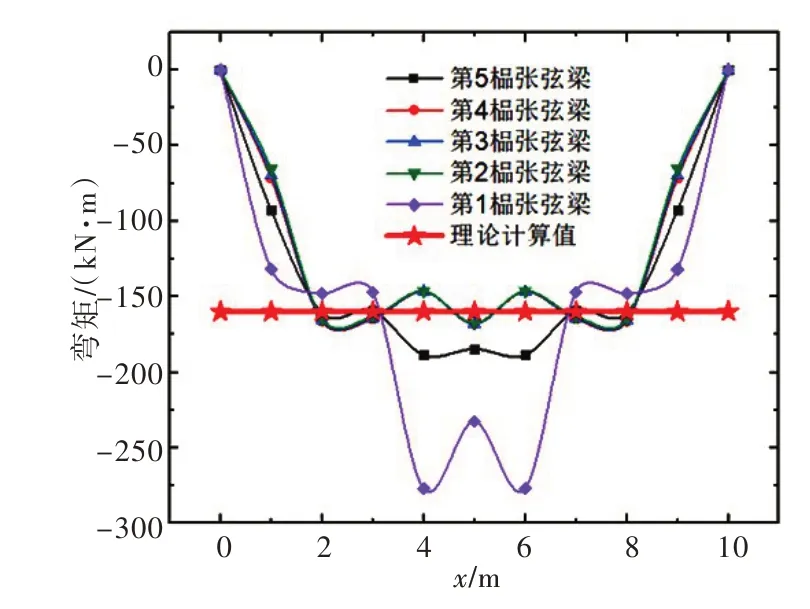
图29 张弦梁弯矩

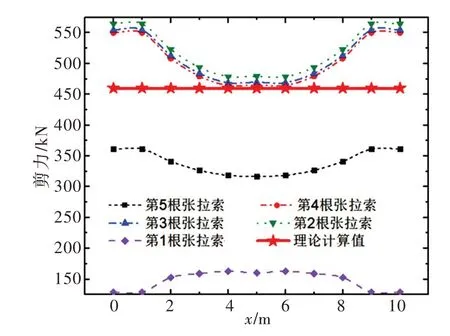
图30 张拉索轴力

表10 牛腿和立柱内力

5 结论

（1）基于“柔性消能”理念，结合张弦梁结构和竖向预应力锚杆技术，克服传统防治结构截面尺寸大、深埋和不经济等问题，改善被动受力的状态，提出一种新型地锚张弦梁式泥石流格栅坝。该结构既可改善结构受力性能、增加结构整体抗冲击能力、保证结构安全可靠，又能减小结构构件截面尺寸、节约成本、便于现场施工组装和后期运营维护，设计理念新颖、技术先进可行、工艺简单，是一种轻柔性防治结构，具有较好的应用前景。

（2）根据泥石流荷载分布和结构受力特征，给出了新型地锚张弦梁式泥石流格栅坝各构件简化的内力计算公式。基于结构内力计算方法，利用Python 语言和Qt Designer 软件，开发了界面友好、操作简单和实用的设计计算软件。

（3）结合算例，对新型地锚张弦梁式泥石流格栅坝进行了内力求解。结果表明：竖杆易发生剪切脆性破坏；立柱内力最大，破坏将危及整个结构的安全，后果严重。可在实际工程应用中借鉴抗震设计中的“强柱弱梁”概念，考虑承载力储备，保证结构的安全性。

（4）利用SAP2000 建立了新型地锚张弦梁式泥石流格栅坝有限元模型，分析了结构的整体受力。验证了构件简化计算方法的合理性和本文方法计算值的正确性。结果表明变形协调仅使底层张弦梁与竖杆内力偏大，其它构件相互受力影响较弱，实际工程应用时，应着重验算底层构件，防止其破坏；本文简化方法计算值最大误差为23%，能较准确地反映结构的受力特性，具有一定的合理性，可为新型地锚张弦梁式泥石流格栅坝的设计提供理论依据。

（5）本文仅针对所提新型地锚张弦梁式泥石流格栅坝内力计算方法进行了分析，为了推动该结构在工程中的应用，还需开展结构的模型试验、稳定性和可靠度等方面的研究。