基于分形维的混凝土裂纹扩展及损伤演化过程研究

殷亚娟，任青文，沈 雷，韩 衍

（1. 河海大学 水利水电学院，江苏 南京 210098；2. 河海大学 力学与材料学院，江苏 南京 210098）

1 研究背景

作为典型的准脆性材料，混凝土在细观上为多相介质组成的复合材料，受力过程中所表现出的非线性应力-应变关系是细观非均质损伤演化过程的宏观表现。材料的损伤伴随着从初始状态开始直至结构完全丧失承载能力的整个受力破坏过程。这一破坏过程实质上是内部细观微裂纹的萌生、扩展、成核和贯通的连续损伤演化过程。混凝土破坏（承载能力丧失）只是裂纹发展的最后阶段，它只能在很小程度上揭示其损伤演变的历史和特征，要真正的描述混凝土破坏的非线性特征，必须追溯到其初始裂纹的分布、裂纹扩展和损伤演化过程，从微裂纹动态演化和材料损伤的角度出发，寻找其演化机理及失稳破坏的依据［1］。但是，外界条件的复杂性和混凝土自身的非线性使得裂纹的动态演化规律研究十分困难。

随着科技的发展，CT 扫描、数字图像相关（Digital Image Correlation，DIC）技术、声发射等技术为研究混凝土的裂纹发展提供了有力的工具。Chotard 等［2］对水泥进行了CT 扫描试验，分析了其水化过程中结构的变化规律。Landis 等［3］和Elaqra 等［4］基于CT 扫描技术对砂浆试件内部裂纹的发展进行了研究。文献［5-7］采用CT 检测技术对混凝土试件静、动力单轴拉伸和压缩破坏过程中的材料内部细观结构及微裂纹变化的特点进行了研究，并基于损伤裂纹做了定量分区。Lawler 等［8］基于DIC 技术，对混凝土破坏时的表面裂纹形式进行了研究，并利用CT 扫描技术对试样内部的裂纹进行了三维分析。雷冬等［9］采用DIC 技术进行了混凝土材料表面损伤应变场的测量。文献［10-11］采用声发射技术对荷载作用下的混凝土损伤进行了监测，研究发现声发射现象的产生行为与混凝土内部的损伤密切相关。胡少伟等［12］研究了混凝土断裂过程中的声发射特性，发现声发射参量可以较好的表征混凝土裂纹的起裂时刻。赖于树等［13］探讨了声发射参数与混凝土破坏过程各阶段的对应关系，研究表明混凝土材料的破坏不是瞬间完成的，而是由于其内部微细裂纹的演化形成更大的宏观裂缝导致的。李杰等［14］研究了混凝土破裂过程中伴随的声发射现象，通过建立混凝土破裂过程中内部结构状态变化（损伤演化）和声发射特征的对应关系，证明了声发射过程包含着材料临界断裂的突变信息。以上研究表明，这些技术是研究混凝土破裂过程的有效手段。但是CT 试验主要通过图像分割方法提取裂纹或孔隙，对裂纹或孔隙的统计只是不同层位CT 图像或剖面图像，不能全面反映裂隙在空间的分布状态，且受扫描断面和扫描次数的影响，试验结果较为离散。DIC 技术主要关注于试件表面变形前后的散斑图像，而对其内部变形特征无法捕捉，不能全面反映试件变形特征。声发射过程中会伴随较强的杂质噪音干扰，其结果受去噪处理方法的影响较大，且难以将细观破坏定量化。随着计算机技术的高速发展，以实验结果为基础，立足于对混凝土细观结构的认识，学者们提出了许多研究混凝土破坏的细观力学数值模型和方法［15-17］。这些模型假定混凝土是砂浆基质、骨料和两者之间的过渡区组成三相复合材料，用材料细观层次上的本构关系来模拟复杂的宏观断裂过程，其优势在于可以借助细观有限元模型进行损伤破坏的追踪模拟。特别对于混凝土拉伸试验，实际操作中受拉试验较难完成，整个试验过程耗时长，加载控制不容易掌握，且试验成功率低，这时用数值模拟方法研究混凝土单轴拉伸可以弥补试验的欠缺。

材料的损伤破坏是一个连续过程，在此过程中各个阶段是如何过渡和转变的，试件在单轴拉伸破坏过程中，全过程应力-应变曲线上对应于出现宏观裂纹的位置往往滞后于峰值点［1］。李兆霞［18］认为从材料应力-应变曲线上的失稳点（峰值点）到宏观裂纹出现的这一阶段是材料性能研究中损伤力学到断裂力学的过渡阶段（即损伤之末，断裂前兆）。如果把出现宏观裂纹的状态假设为临界状态，标志着材料从均匀损伤向局部破坏转变，那么如何确定相应于临界状态点的损伤阈值，吕从聪［19］根据损伤演化曲线的发展形态，将损伤值0.8 作为宏观裂缝出现的损伤阈值，王高辉［20］则将损伤阈值选取为0.75。

然而这些还只是处于定性说明阶段，缺乏定量分析。此外，已有的研究表明，不管是实际混凝土的开裂过程还是混凝土损伤开裂的细观数值模拟结果，裂纹的发展变化都没有明显的数学规律，传统的分析方法难以描述［16］。因此，本文在细观层次上引入分形理论和方法研究混凝土损伤演化规律和裂纹扩展过程。

2 研究方法

2.1 盒维数分形是由法国数学家Mandelbrot 提出的一门数学科学［21］，是专门研究不规则问题的有效方法。该数学分支创立于1970年代，以自然界不规则以及杂乱无章现象为研究对象，产生后很快被用于材料微细观结构及其受力变形特性研究［22-24］。分形维数是传统维数（整数维）概念的推广，是一种度量自然界中复杂形态的新方法。目前分形维数的计算有多种方法，其中盒维数是一种有效的计算图形分形维方法，对于损伤裂纹的研究，其计算公式如下：

式中：F 为所求损伤裂纹分布的盒维数；L 为正方形盒子的边长，以1/Lk变化（k=0，1，2，…）；N(L)为用边长为L的盒子去覆盖损伤裂纹分布所需要的盒子数。

通过不断改变盒子尺寸来改变覆盖图形的盒子总数，绘制lg N ( L )-lg(1 /L )关系曲线。如果曲线满足线性关系，则证明图形具有自相似性，可以利用分形几何理论来研究。分形维越大，表示混凝土试件损伤发生越多，裂纹分布越复杂。

2.2 基于裂纹分形维的损伤变量研究表明，裂纹分形维可以很好地描述混凝土受力过程中裂纹的分布，即裂纹萌生、扩展、贯通及最后破坏的破裂过程［6，23］，因此，可以将裂纹分形维作为定量的损伤状态参数来描述混凝土受力中裂纹的演化过程，损伤变量的定义形式比较多样［25-26］，本文根据裂纹分形维的计算结果，定义分形维与损伤变量的关系式如下：

式中： f0为材料整个试件完全破坏时累积裂纹分形维绝对变化量之和； fmd为第m 个分析步时累积裂纹分形维绝对变化量之和。

其中：

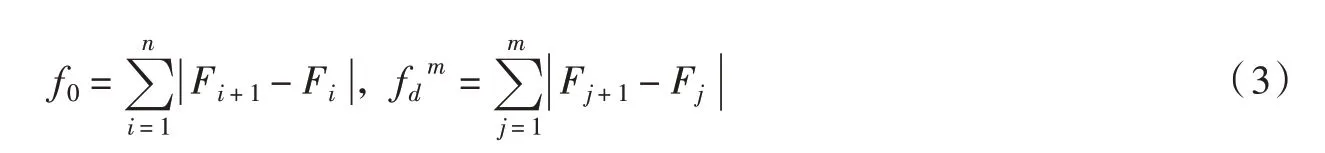
因此，得到损伤变量具体计算公式如下：

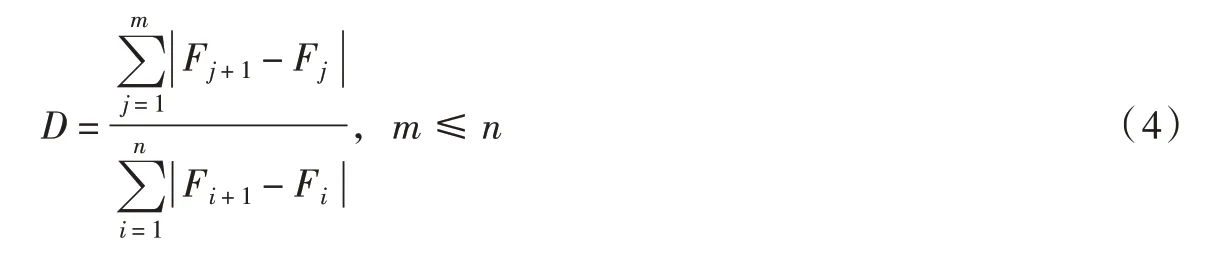
式中：Fi、Fj分别为第i 和j 个分析步对应的裂纹分形维；n 为试件完全破坏总共经历的分析步。

损伤变量D 取值范围为0～1，对应不同程度的损伤，D=0（即损伤值为0）对应无损状态，D=1（即损伤值为1）对应完全损伤（破坏）状态。基于裂纹分形维的损伤变量的具体计算流程参见图1。

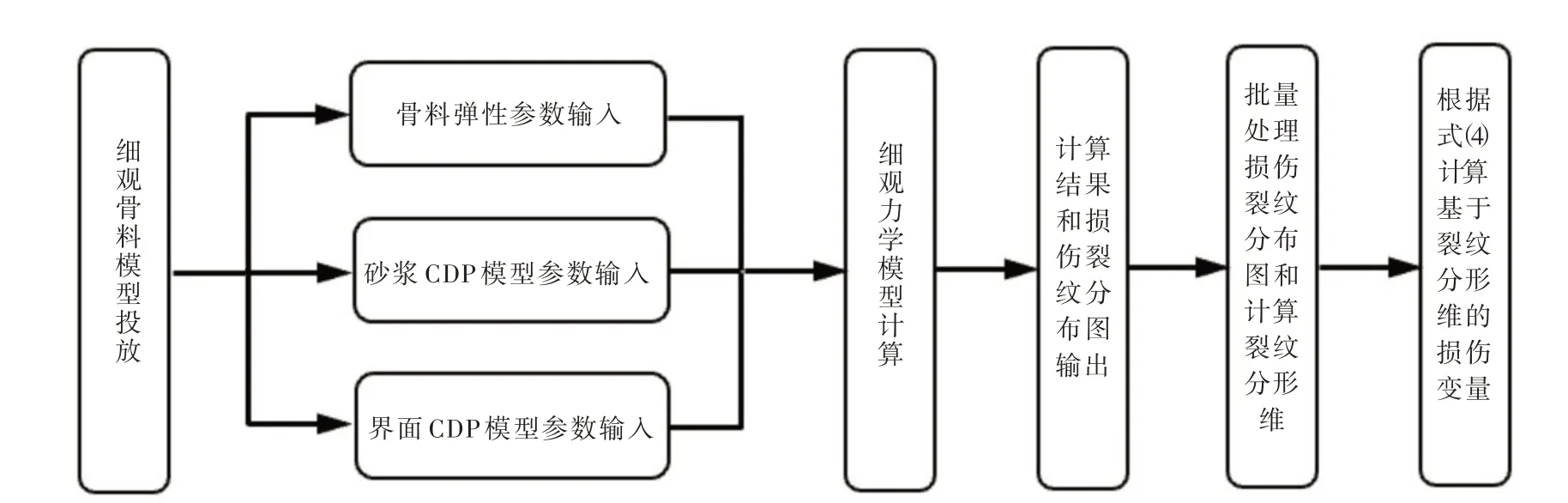
图1 基于裂纹分形维的损伤变量计算流程

2.3 混凝土塑性损伤（CDP）模型CDP（Concrete damage plastic model）模型能够模拟水泥基材料的拉伸开裂和压缩碎裂现象［16，27］，以及混凝土动力加载和循环加载力学行为。单轴应力状态下，CDP 模型应力应变曲线考虑了损伤引起的等效塑性应变（包含拉伸等效塑性应变和压缩等效塑性应变）。依据试验，模型假定单轴加载时拉伸损伤因子dt与压缩损伤因子dc分别随拉伸等效塑性应变压缩等效塑性应变增加而增加［28］。则由损伤因子控制的应力-应变关系可表示为：

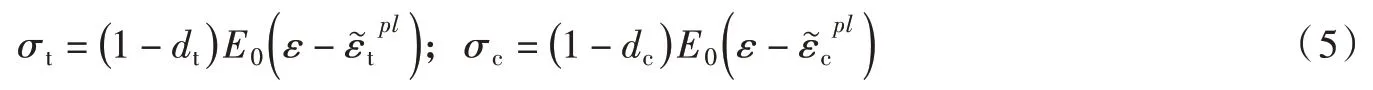
式中：下标t和c分别表示拉伸和压缩；E0为初始弹性模量；σ为应力。

式（5）中的损伤因子计算公式为：

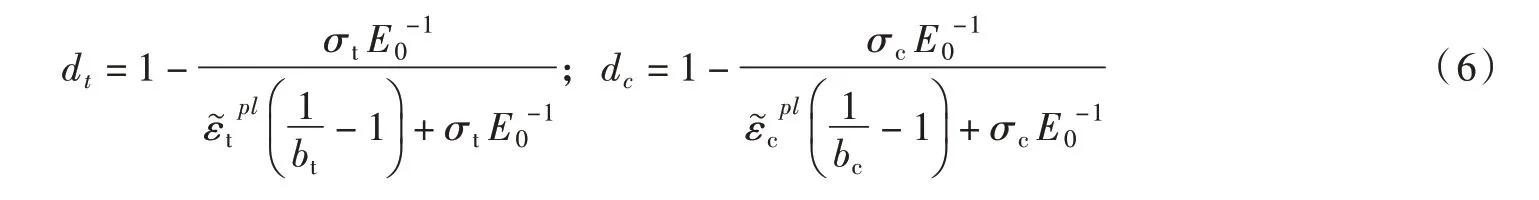
其中，bt、bc分别为非弹性应变中塑性应变的比例，本文采用文献［29］的建议值，bc=0.7 和bt=0.1，该值与循环加卸载试验数据比较吻合。

图2 为CDP 模型单轴应力-应变关系曲线。多轴应力状态由单轴应力状态值拓展得到。关于该本构模型的详细描述，可参考文献［30-31］。

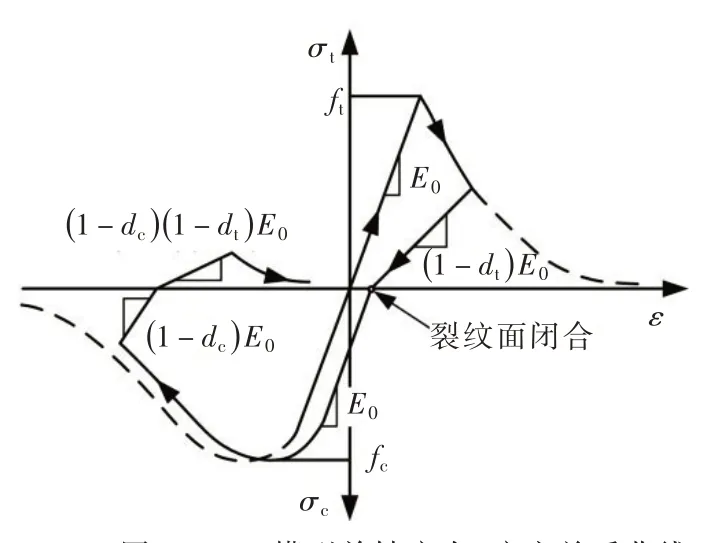
图2 CDP 模型单轴应力-应变关系曲线

2.4 突变性判据突变性判据表示系统处于极限平衡状态，它将由一种平衡状态向另一种平衡状态或非平衡状态转变，也就是说，系统的状态发生了突变［32］。突变性判据认为任何能够反映系统状态突变的现象都可以作为失稳判据，如位移突变判据，能量突变判据等等。本文利用混凝土损伤开裂过程中裂纹扩展的分形维变化规律来研究“均匀”损伤到局部破坏的临界判据。

3 混凝土拉应变与裂纹分形维关系的细观数值模拟

3.1 细观模型与计算参数采用基于Monte Carlo 法的随机骨料投放软件［16］生成二维细观混凝土正方形试件，试件边长为200 mm，骨料含量为40%，粒径范围为5 ~ 40 mm。建立了含界面过渡区（Inter⁃facial Transmission Zone，ITZ）的二维混凝土三相复合材料数值模型（图3）。

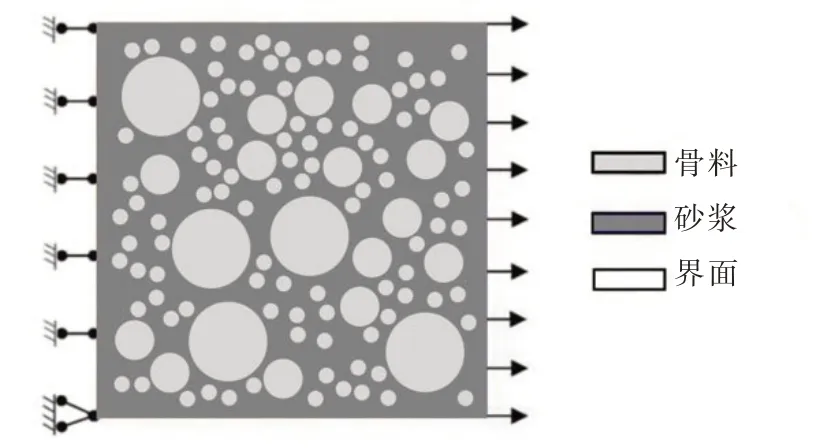
图3 混凝土细观力学模型

Scrivener 等［33］指出，ITZ 厚度约为40 ~ 50 μm，但考虑到计算工作量，本文中ITZ 厚度取100 μm。在混凝土细观研究中，ITZ 的材料参数非常重要，但目前该参数较难由试验测得。通常认为ITZ的力学性能与水泥砂浆类似，略小于水泥砂浆［15-16，27］，本文ITZ 参数的选取按砂浆参数的80%进行折减，具体计算参数见表1。水泥砂浆和ITZ 力学本构模型均使用CDP 模型［16，27-28］。相比于砂浆基质及界面区，骨料具有较大的拉、压强度，在静态甚至低速动态加载情况下，裂纹往往绕过强度较大的骨料颗粒而从界面及砂浆中穿过［34-35］，因而可假定骨料为线弹性体［16，27，35］。混凝土试件的数值计算中，为了避免网格效应，采用拉伸应力-位移模型替代应力-应变模型［16，23］。

表1 各组分的计算参数［16，27］

3.2 网格尺寸的选择对上述细观混凝土试件进行单轴拉伸，试件一端固定拉伸方向位移，另一端使用位移控制荷载，当拉伸应变达到600 με 时停止。裂纹分形维的计算需要提取损伤细节，因此需要研究网格划分对结果的影响。对上述模型以四节点平面应力四边形（CPS4R）单元剖分网格，见图4，利用统一尺寸划分网格，网格尺寸分别选取1.0、1.5、2.0、2.5 和3.0 mm；网格数量分别为54 828、26 622、16 738、9963 和8715。不同网格尺寸的最终裂纹分布图和裂纹分形维见图5。

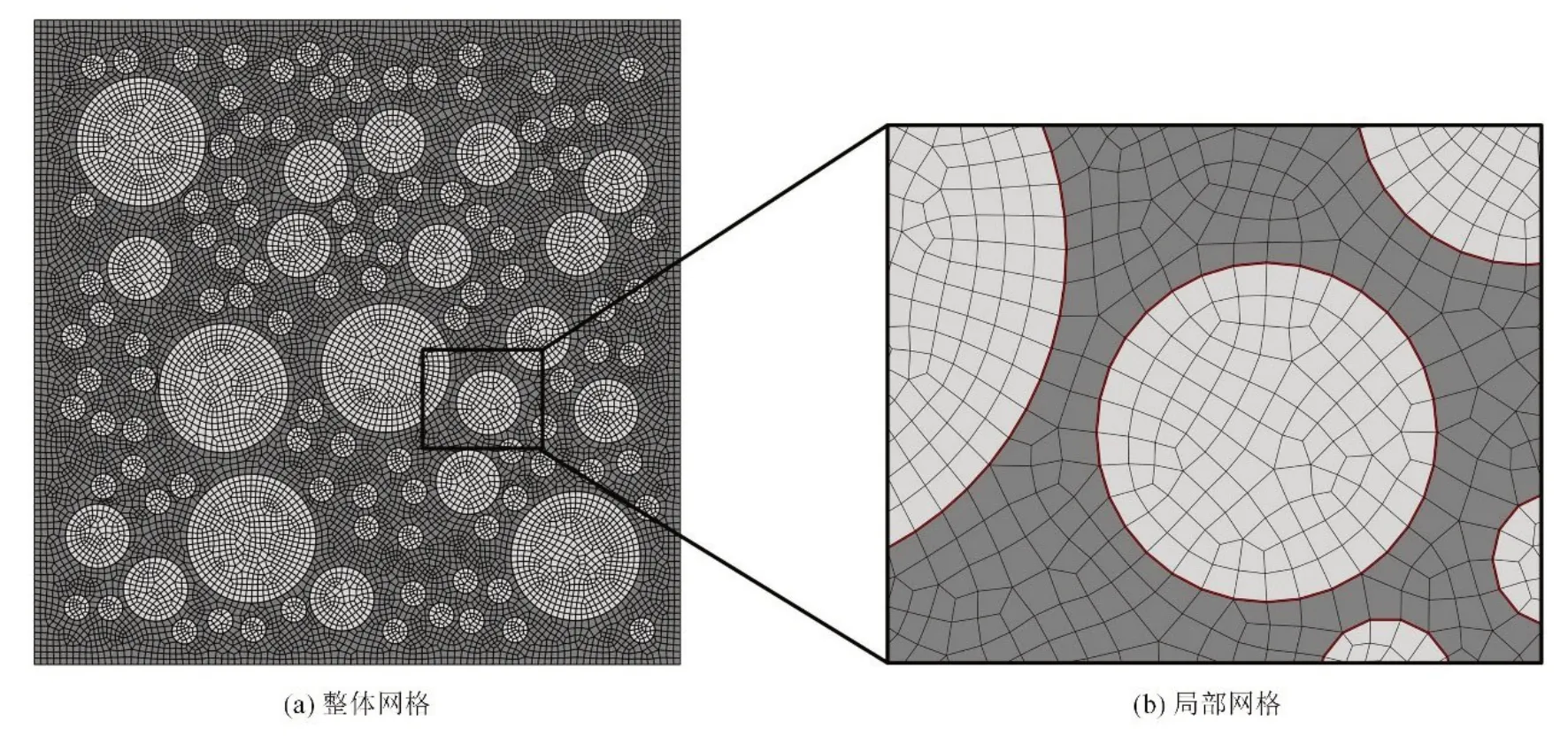
图4 细观模型有限元网格剖分图

从图5 可以发现，随着网格尺寸大小的改变，最终的裂纹分布形态没有显著的改变，裂纹路径分布基本一致。网格尺寸1.0、1.5、2.0、2.5 和3.0 mm 最后的裂纹分布分形维分别为1.17、1.15、1.16、1.22 和1.23。整体上裂纹分形维随着网格尺寸的增大而增加，但最大差值约为6.7%，说明网格尺寸对裂纹分形维的影响很小。

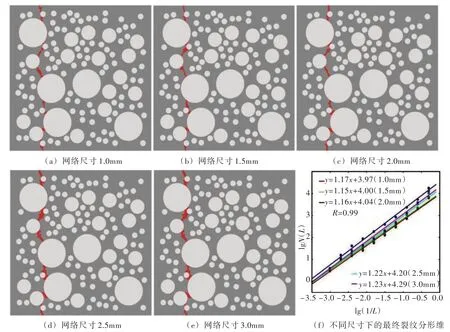
图5 不同网格尺寸的最终裂纹分布和裂纹分形维

不同网格尺寸的应力-应变曲线以及裂纹分形维-应变曲线见图6。从图6 中可以看出，随着网格尺寸的改变，应力-应变曲线有些许不同，但相差极小。峰前行为基本重合，峰值点最大差值约为0.9%，峰后软化段大体相似。同时发现，随着网格尺寸的改变，裂纹分形维曲线有些许不同，但是整体趋势都较为一致，从无到有经过平稳增长会出现一个小幅度下降突变后再继续平稳增长。可见网格尺寸对应力-应变曲线和裂纹分形维-应变曲线的影响很小。

此外，从图6 可以发现，5 组损伤演化曲线整体趋势也大体相似，都是从0 开始增大直至趋近于1。开始的线弹性阶段损伤发生极少，几乎可忽略，损伤值接近于0；然后进入损伤加速发展阶段，表现为损伤值开始迅速增大；最后处于损伤收敛阶段，此时损伤值的增长趋势开始变缓，平稳趋近于1。这些过程与损伤力学基本观点相符［36］，表明本文提出的损伤计算方法可行且有一定的适用性与普遍性。

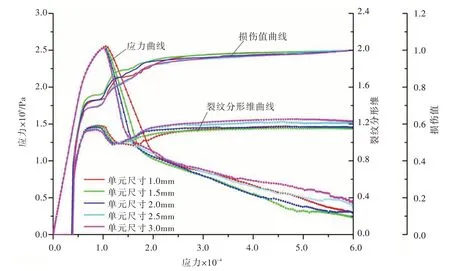
图6 不同网格尺寸的应力-应变曲线以及裂纹分形维-应变曲线

综上所述，网格尺寸对裂纹形态和分形维、应力应变曲线和应力峰值、损伤演化曲线的影响都很小，再考虑计算效率，本文接下来选用网格尺寸为2.0 mm 的结果说明裂纹扩展和损伤演化过程。

3.3 裂纹扩展和损伤演化过程混凝土拉伸应变对外界因素的敏感度比较小［37-38］，在试验操作中，混凝土局部的应变可以直接测量，而与应力有关的量可能需要通过假定的本构关系或界面换算才能得出。且考虑拉伸应力-应变全曲线，峰后下降段中应力不再增加而应变却是单调增加。因此，应变可以更好地表征损伤发展过程。网格尺寸2.0 mm 的模型计算相关参数结果见表2。图7 给出混凝土受拉破坏过程损伤值和裂纹分形维随应变的变化规律，图8 给出了混凝土裂纹的发展演化过程。

表2 损伤发展过程中各点对应的参数值

对照图7 和图8，可以很好理解混凝土损伤演化的全过程，具体如下。

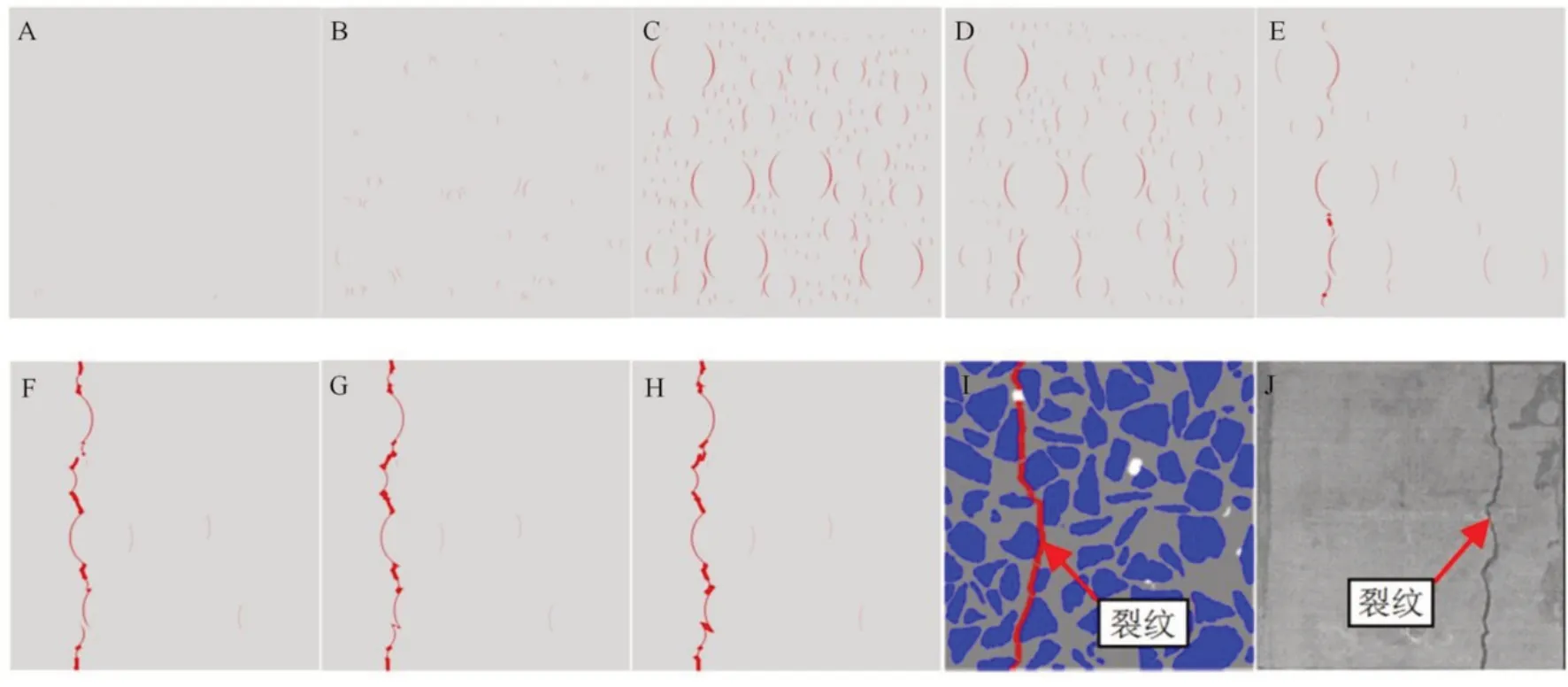
图8 各点损伤裂纹发展（A—H 对应图7）与前人数值模拟［39］和试验［40］结果

A 点，损伤微裂纹萌生点。A 点只有少许的界面损伤微裂纹萌生，损伤裂纹分形维为0.58，损伤只分布在一些细小区域内，几乎不可见。此时，A 点损伤值为0.36，整体损伤较小，材料性质没有发生重大变化，试样整体表现为线弹性，对应的应变值为3.94×10-5。

B点，弹性极限点。随着外荷载的增加，出现了明显的界面微裂纹，B点之前是线弹性阶段，之后试件进入非线性阶段，B点是弹性极限点。此时的裂纹分形维为0.90，损伤值为0.56，应变值为5.00×10-5。

C 点，分布式裂纹最多点。C 点是损伤在整个试件内“均匀”发展（分布式裂纹）的最多点，此时，整个试件中垂直于拉伸方向的全部界面都出现损伤裂纹，形成散布的零星短小裂纹分布在整个试件，裂纹分形维曲线达到极大值，C 点裂纹分形维为1.17，损伤值为0.73，应变值为8.61×10-5，整体表现为非线性。

D 点，峰值应力点。此时的裂纹分形维为1.12，损伤值为0.76，峰值应变为1.02×10-4，D 点呈现出裂纹整体趋势向某局部区域（试件的最薄弱面）聚合。此时，裂纹趋于局部化发展，试图形成裂纹聚合区，其他区域损伤裂纹部分回弹。

E 点，进入局部破坏阶段的临界状态点。E 点裂纹分形维为0.98，是应力峰值点之后分形维曲线（图7 中的半空心三角曲线）的极小点，也是分形维曲线形态的突变点。E 点损伤值为0.84，应变值为1.23×10-4。E 点之前，分布式裂纹向薄弱面聚合，E 点之后裂纹聚合区形成，宏观裂纹出现，可认为E 点是临界状态点，是损伤和断裂的分界点，此时，试件开始出现宏观裂纹，材料随即进入局部破坏阶段。

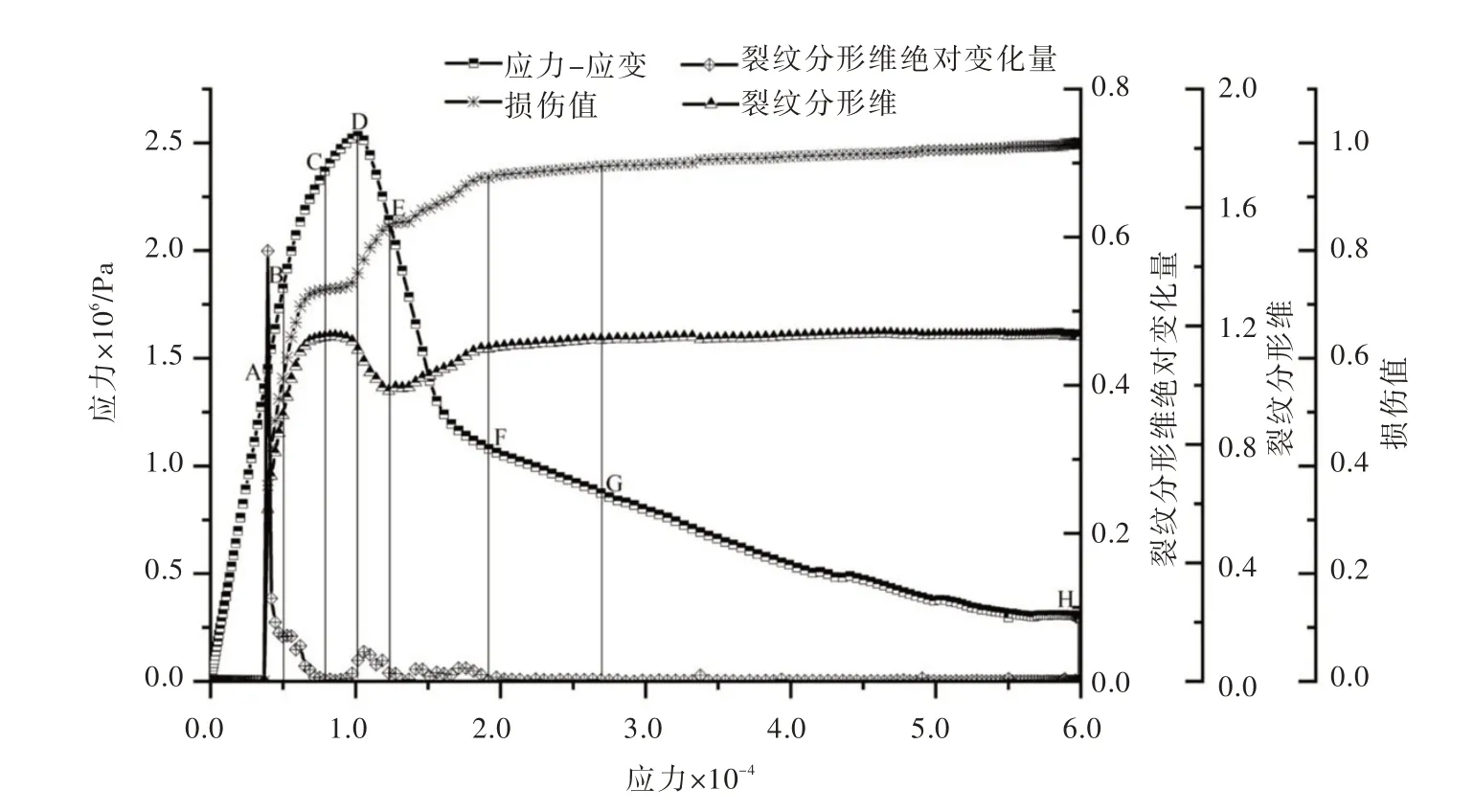
图7 混凝土损伤过程（网格尺寸为2.0mm）

F 点，裂纹分形维绝对变化量的平稳点。从裂纹分形维绝对变化量曲线可以看出，F 点之前，裂纹分形维绝对变化量起伏变化明显，说明损伤裂纹路径在不断的变化发展，F 点之后，裂纹分形维绝对变化量变得平稳，说明裂纹开裂（局部破坏）的主要路径已形成。此时，损伤继续发展，局部破坏路径不断扩大，宏观裂纹迅速扩展，F 点裂纹分形维为1.12，损伤值为0.94，应变值为1.92×10-4。E到F 段试件整体表现为应力迅速下降，而变形增加不大。

G 点，宏观开裂区基本形成点。G 点裂纹分形维为1.15，损伤值为0.96，应变值为2.69×10-4，此时，试件的宏观开裂区基本形成。G 点以后，变形增长加快而应力下降减慢，这是由于此时开裂区以外的弹性区的回缩大致结束，变形增长基本上是裂缝扩展的结果。

H 点，试件完全破坏点。H 点对应最后破坏呈现的宏观裂缝形态，分形维为1.16，损伤值为1，应变值为6.02×10-4，裂缝形态与G 点相似，但此时，裂缝贯穿全截面，试件断裂成两段，断面凹凸不平，试件完全破坏。

上述分析表明，分形维的变化规律可以反映试件受力时的损伤演化过程，能够定量地描述混凝土材料损伤演化的特性，整个数值模拟结果与文献［39-44］的数值模拟与实验结果相符，其中图8（I）显示了文献［39］的数模结果，本文数模结果与其一致且细节更加清晰，图8（J）给出文献［40］的实验结果，其裂纹形态与本文数模结果也相当接近。此外，文献［5］中对单轴拉伸的混凝土试样进行了6 次CT 扫描，并利用盒维数计算CT 扫描断面的分形维。证明了混凝土受力破坏滞后于峰值强度，且扫描结果显示混凝土破坏断裂面的分形维整体呈递增趋势，这与本文裂纹分形维的整体增长趋势一致。但是，由于混凝土破坏的脆性特征，实际试件在受拉达到峰值后，CT 扫描时试样已发生破坏，难以真正捕捉到试样拉伸破坏时裂纹的演化过程。而且有限次数的扫描使得CT 试验结果是跳跃的，易遗漏一些重要的过程细节，更难以找到试件进入局部破坏阶段的临界点。本文的数值模拟弥补了这一缺陷。

混凝土在单轴拉伸过程中细观裂纹经历了细小裂纹萌生（A 点到B 点阶段）、分布式裂纹生长（B点到C 点阶段）、细观裂纹聚合（C 点、D 点及E 点阶段）、宏观裂纹形成与扩展（E 点、F 点及G 点）、发生断裂（G 点到H 点）的损伤跨尺度演化过程。其中，E 点是整体统计意义上的“均匀”损伤进入局部破坏阶段的临界点，此时开始出现宏观裂纹，E 点可认为是损伤到断裂的分界点，对应于裂纹分形维曲线的突变点，相应的损伤值为0.84。

3.4 级配对混凝土损伤开裂的影响选取尺寸200 mm，骨料含量40%，根据文献［45］的相关规定，生成一级配混凝土试件含小石（等效粒径12 mm）141 颗；二级配混凝土试件含小石（等效粒径12 mm）78 颗，中石（等效粒径30 mm）10 颗；三级配混凝土试件含小石（等效粒径12 mm）47 颗，中石（等效粒径30 mm）7 颗，大石（等效粒径60 mm）2 颗（图9）。网格尺寸划分均为2.0 mm，利用裂纹分形维，研究不同级配的细观混凝土损伤开裂过程。3 种级配的混凝土试件应力-应变曲线以及裂纹分形维-应变曲线见图10。

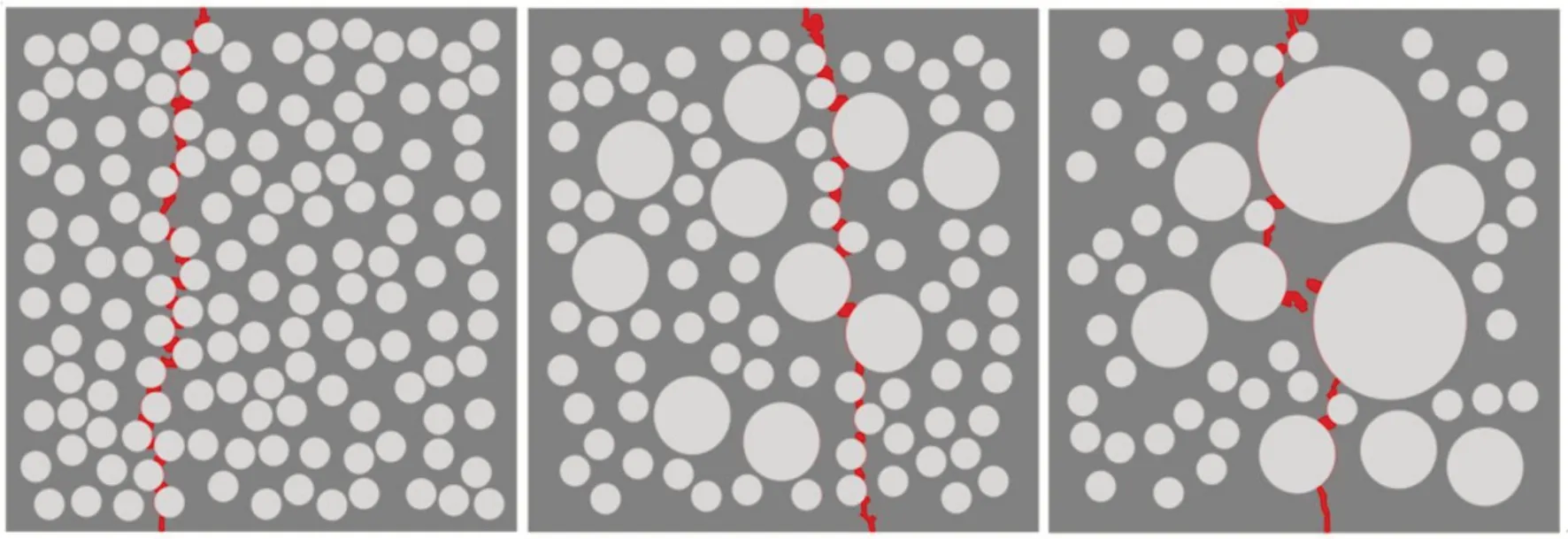
图9 不同级配的裂纹分布

从图9 可见，3 种级配的裂纹演化过程较一致，裂缝首先发生在力学性能相对薄弱的界面过渡区中，进而扩展进入砂浆基质，并且在扩展过程中均绕过强度相对较高的骨料颗粒，最终形成贯穿整个试件的主裂缝，在宏观尺度上垂直于主拉应力。但裂纹的形态和分布略有不同。由图10 发现，虽然3 个级配的应力-应变曲线和裂纹分形维曲线的整体趋势一致，但应力值和裂纹分形维都随着混凝土试件骨料级配数的增加而减小。这是因为随骨料级配数的逐渐变大，骨料颗粒也逐渐变大，当试件尺寸和骨料含量相同时，一级配所含骨料颗粒最多，相应的骨料界面也越多。而界面是混凝土的薄弱部位，试件的破坏萌生和发展均在界面附近，一级配骨料颗粒增加使得界面数量变多，从而使得试件的整体破坏路径增多，裂纹扩展路径变多，则裂纹发展需要消耗更多能量，从而提高了开裂区应力。从裂纹分形维曲线看出，一级配试件的整个损伤过程中裂纹分形维都较大，说明其裂纹扩展路径曲折。但另一方面，由于一级配开裂路径上的界面最多，试件在局部区域，尤其是主裂纹形成后，破坏路径也更容易贯通，所以更容易发生脆性破坏。此外，一、二、三级配的分形维曲线都有突变点，标志着试件从整体“均匀”的分布式损伤进入局部破坏阶段，对应的损伤值分别为0.817、0.806、0.809。因此，本文建议应力峰值点之后裂纹分形维-应变曲线的突变点为进入局部破坏的临界点，相应的损伤值大约在0.8 左右，该值可作为宏观裂纹出现的损伤阈值。

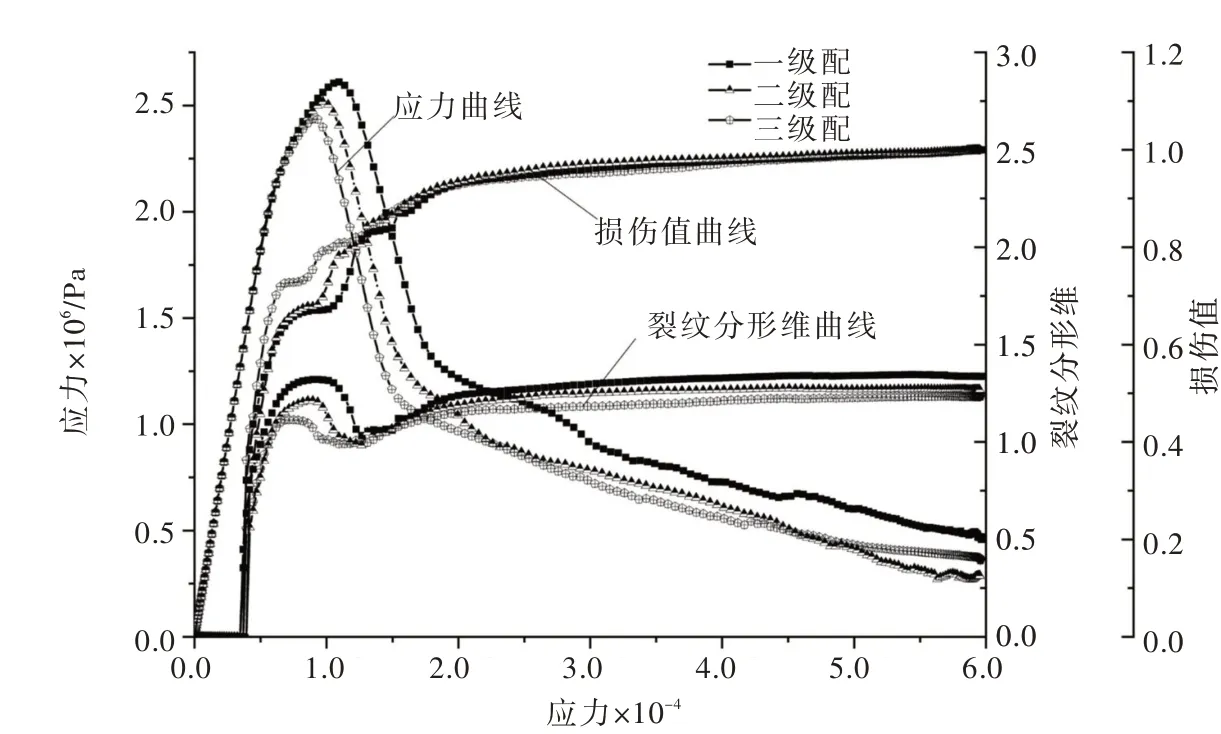
图10 不同级配的混凝土试件应力-应变曲线以及裂纹分形维-应变曲线

4 结论

基于混凝土细观力学模型，对多组混凝土试件的单轴拉伸力学行为进行数值研究，提出一种基于裂纹分形维的计算损伤变量的方法，利用分形维对整个混凝土受力开裂过程中的裂纹分布进行表征。得出如下结论：（1）细观模拟的裂纹形态与试验结果相符；混凝土在单轴拉伸过程中在整体统计意义上经历了从“均匀”损伤到局部破坏的过程，即细小裂纹萌生、分布式裂纹生长、细观裂纹聚合、宏观裂纹形成与扩展、发生断裂的损伤跨尺度演化过程。（2）裂纹分形维能够更好地反映混凝土材料损伤的变化过程，可以定量描述材料损伤演化的特性；发现了混凝土“均匀”损伤至局部破坏的临界点；细观模拟得到的应力-应变曲线、裂纹分形维曲线、损伤演化曲线受网格尺寸的影响小；随着混凝土试件骨料级配数的增加，骨料颗粒和界面减少，整体耗能降低，应力峰值和裂纹分形维均减小。（3）建议应力峰值点之后的裂纹分形维-应变曲线突变点为混凝土材料从“均匀”损伤进入局部破坏的临界点，是损伤和断裂的分界点，相应损伤值在0.8 左右，该值可作为混凝土出现宏观裂纹的损伤阈值。