基于顾客到达拟合的立体车库搬运器待命位设计策略

李建国，杨波，马尚鹏

（兰州交通大学，自动化与电气工程学院，兰州 730070）

0 引言

城市汽车保有量快速增长，停车难问题日益显著，发展自动化立体车库成为缓解停车难问题的有效途径。平面移动类停车设备具有高密度、高可靠性、高自动化程度及高存取车效率等优点，但存在存取效率低，顾客等待时间长等问题，优化立体车库待命位策略，可以缩短任务响应时间，减少顾客存取车等待时间。

Antonella等[1]指出待命位原理即在下一任务未知的情况下，利用空闲时间移动搬运设备等候待命的位置，该位置很可能是下一任务所在位置，此段空载运行时间很可能缩短下一任务的响应时间。Meller等[2]证明在高系统利用率下系统中无待命位可言。Bozer 等[3]针对仓库系统首先提出待命位策略。Egbelu等[4]通过模拟研究比较了Bozer等[3]的4个待命位策略并提出两个动态待命规则。Peters等[5]在Bozer等[3]的基础上，开发了封闭形式的分析模型。Park等[6]表明当下一个任务为存储请求的概率大于1/2时，则输入口为最优待命位。Byung[7]提出均匀分布下的自动化仓库堆垛机的待命位置可以根据某类请求发生的概率确定。Roy等[8]基于半开放排队网络理论模型研究待命位置、交叉通道位置对搬运设备性能的影响。Liu 等[9]提出了一个在输入输出(I/O)待命位策略下的双命令连续旅行时间模型。Xu等[10]针对单指令周期(SC)，建立双指令周期(DC)旅行时间模型下的输入输出待命位策略。Regattieri 等[11]开发了一个新的连续旅行时间模型，研究已有待命位策略中的最佳待命位策略。马永杰等[12]提出“多质点重心法则”的堆垛机出库待命位策略。Yu 等[13]研究输入和输出位置分别位于通道两端的自动化立体仓库的待命位策略。Hu等[14]针对AGVS 系统提出了分布式待命位策略模型。贺云鹏[15]提出依据顾客存取车到达状态动态调整存车优先、取车优先及原地待命的待命位策略并结合车位分配对待命位策略进行优化研究。

综上，待命位策略作用于系统空闲期，依赖于下一任务发生类型及位置预测，在平面移动类立体车库中，反映为顾客等待时间、搬运器服务时间、运行能耗及利用率的均值性指标。本文在既有研究的基础上，依据实际工程数据，通过对顾客到达过程及车辆库内停留时长服从分布进行拟合，依据拟合结果预测下一存、取任务类型及最大概率出库顾客车辆所处位置，进而设计了以共同出库路径分叉节点为出库待命位置的待命位策略。

1 问题描述与建模

1.1 立体车库结构模型

本文研究对象(平面移动式立体车库)属于AVS/RS系统，搬运设备移动空间为三维空间，不同于AS/RS、AGVS 仓储系统中二维空间[16]。立体车库实体模型如图1所示，基本构成包括车辆进出的I/O，用于车辆存取操作的搬运器(Rail Guided Vehicle，RGV)及用于车辆水平移动的辅助轨道，用于车辆跨层搬运的升降机(Lift)，车位分布于巷道两侧，车库包含p层q列2排车位，车位高度为g，宽度为l，其中，x值表示所在位置的列坐标，y值表示所在位置的排坐标，z值表示所在位置的层坐标。

1.2 立体车库调度模型

根据1.1 节立体车库实体模型，在不考虑RGV运行过程中拥堵避让的假设下，建立该车库中RGV及Lift的调度模型，考虑到顾客满意度及开发商运营成本两方面指标。确定以顾客平均等待时间Tw、RGV 平均服务时间Ts、平均能耗TQ及平均利用率Tρ为车库运行效率指标。各指标计算公式为

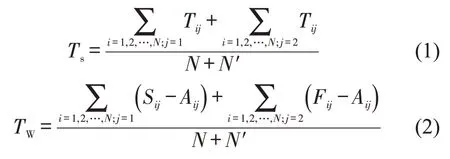
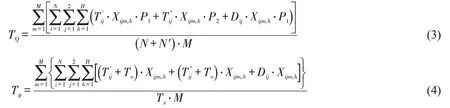
式中：i为顾客车辆编号，i∈N；N为到达顾客i的总数；j∈{1 ,2} ，j=1为车辆入库阶段，j=2 为车辆离库阶段；N′为离去顾客i的总数；Oij为编号为i的顾客处于第j阶段时的任务；h为任务Oij的编号；Tij为任务Oij接受的服务时长(不包含RGV 操作时间及出入车厅耗费时间)；Fij为任务Oij的结束时间；Sij为任务Oij的开始时间；Aij为任务Oij顾客到达时间；m为RGV 的编号，m=1,2,…,M,M∈Ζ+，M为车库中RGV 总数量；P1为RGV 空载运行牵引功率；P2为RGV 负载运行牵引功率；Ti′j为RGV 执行任务Oij空载运行时间；Ti″j为RGV 执行任务Oij负载运行时间；Dij为RGV 移动至待命位置所需时间；Xijm,h为决策变量，若任务Oij由编号为m的RGV第h个服务则Xijm,h=1，其中h∈H，H为总任务数，否则，Xijm,h=0；To为RGV执行1次存取所需时间；Tz为车库1 d中运行总时间。

1.3 基于拓扑地图法的RGV运行环境模型

拓扑地图法结构化限制的特点，适用于运行环境固定、不存在其他障碍及环境因素的平面移动式立体车库系统。本文选取拓扑地图法构建RGV运行环境模型，将RGV 运行过程中所经路径描述为如图2所示的节点与边的关系。

图2 基于拓扑法的RGV运行环境模型Fig.2 RGV operating environment model based on topology method

图2中，F表示车库总层数，C表示车位总列数，Lift 在第0 列及第C+1 列，各节点之间的连线表示两节点互通性。节点编号按照第0 列到第C+1列，自第1层至第F层从1到（C+2）×F连续计数。服务同一层两个相对位置共同占用一个节点。

2 顾客存取车到达特性分析

2.1 顾客存车到达过程拟合

本文采用西安市某商用立体车库2019年6～7月泊车历史数据，共计1836条，使用文献[17]的拟合方法，得到该车库顾客平均到达间隔时间函数关系为

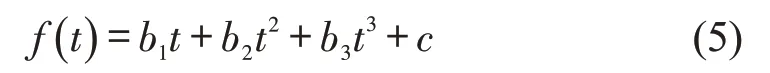
式中：t为顾客到达时间，b1、b2、b3、c分别为三次估计模型的参数，常量c=398.9 ，b1=0.054 ，b2=-4.415×10-6，b3=7.890×10-11。

图3为拟合该车库7月7日(7:00-23:00)顾客到达过程的仿真对比结果，所得结果与文献[17]结论一致，表明该车库顾客到达过程为非齐次泊松过程。

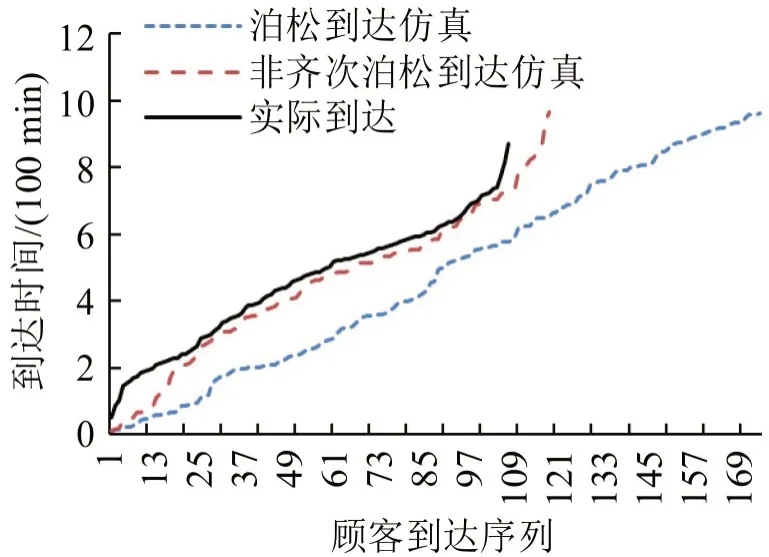
图3 7月7日顾客到达过程仿真对比Fig.3 Simulation comparison of customer arrival process on July 7

2.2 顾客车辆库内停留时长拟合

延用2.1 节历史数据，对车辆库内停留时长进行拟合，所得结论与文献[17-18]一致，服从N(μ,σ2)正态分布，其中，μ=145 min，σ2=240。对该车库7月7日(7:00-23:00)每小时顾客实际存取车辆与通过顾客非齐次泊松到达及正态分布停留拟合所得每小时顾客存取车辆进行对比，结果如图4所示。

利用图4的对比方法，分析计算该车库21个非工作日内顾客每小时实际存、取到达数量与仿真拟合存、取到达数量的误差，得到仿真存、取车数量的平均误差分别为6.36%、15.29%，表明拟合顾客的存取到达过程与车库实际顾客存取过程相符。

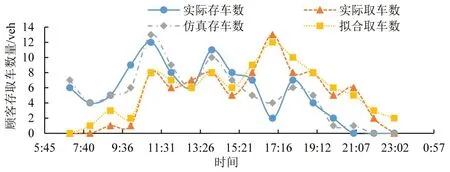
图4 顾客每小时实际存取车数量与仿真数量对比Fig.4 Actual number of customers'access cars per hour is compared with simulation number

3 立体车库待命位策略设计

3.1 待命位置确定

由1.3 节RGV 运行环境模型，将RGV 待命位置分为入库待命位置、出库待命位置。其中，入库待命位置固定为I/O 口(本文车库中I/O 口并列排布，设计入库待命位置即为其中间I/O 口位置)，确定待命位置的关键即为出库待命位置的设计。

记当前空闲RGV 所在位置节点为ε，ε⊂{1,2,…(C+2)×F} ；δt为t时刻发生最大概率出库车辆位置节点集合，δt⊂{1,2,…(C+2)×F} ；根据Dijkstra最短路径算法，若R1表示节点ε到集合δt中第1个出库车辆节点的路径节点集合，依此类推，则Rn表示节点ε到集合δt中最后一个出库车辆节点的路径节点集合，若Rn集合中第1 个节点编号小于等于ε，则记Rn∈U，否则记Rn∈V，其中，U为左侧路径集合，V为右侧路径集合。分别对U及V中各路径集合取交集，则对应交集中最后一个节点即分叉节点，图5为左、右分叉节点示意图。

图5 RGV出库路径分叉节点示意Fig.5 RGV retrieval path bifurcation node diagram

3.2 基于出库路径集合覆盖方法的待命位策略设计

基于出库路径集合覆盖方法的出库待命位策略设计流程如图6所示。

如图6所示，在3.1 节的基础上，选择左、右两分叉节点中一个作为出库待命位置。根据存车到达较早车辆优先出库策略，以U及V路径节点集合中包含各节点所对应车辆库内停留时长的平均值作为选择判断依据，出库节点集中库内平均停留时长较大的一侧对应更大的车辆出库可能性，因此选择库内平均停留时长较大集合对应的出库待命位置为首选出库待命位置。不同RGV空闲开始空闲时刻、位置不同，分别用ϕL,m、ϕR,m表示编号为m的RGV 执行最后一个任务完成时刻对应左、右两出库节点集中各节点对应顾客车辆库内停留时长的平均值，计算公式为

式中：Kcurrent,m为编号为m的RGV 状态空闲开始时刻；Sx1,Sy1,…,Sz1为左出库节点集各节点对应顾客车辆入库开始服务时间；Su1,Sv1,…,Sw1为右出库节点集各节点对应顾客车辆入库开始服务时间，其中，∀{x,y,…,z,u,v,…,w} ∈Ζ+，x,y,…z;u,v,…,w为顾客到达顺序编号；Xlength,m、Ylength,m分别为编号为m的RGV 自空闲时刻对应左、右出库节点集合中包含出库车辆总数。

4 实例验证

以西安市某立体车库为实体模型，利用第2节所得结论，在相同顾客存取车到达过程下，编制原地待命策略、P中值模型待命策略与本文设计待命策略下车库100 d中7:00-23:00(共计23800条任务)的仿真程序。其中，原地待命策略即搬运设备停在最后一个任务结束位置；P中值模型常用于工厂或者仓库的选址，与闲置RGV 待命位置选择问题有相似之处，不同之处在于P中值模型假设了一个完全连通的网络，文献[14]将待命位置问题转化为线性规划问题，得出与P 中值问题相同的公式，称文献[14]中求解待命位置问题的方法为P中值模型待命策略。

该车库实际工程参数包括RGV水平移动速度vh=1 m·s-1；Lift垂直移动速度vv=0.6 m·s-1；RGV空载牵引功率8 kW，负载牵引功率10 kW；车厅排数A=2，车位列数C=21，车位层数F=6；电梯数量L=2；RGV 数量M=3；I/O 数量为3 个，对应坐标分别为(5, 10, 2)、(5, 11, 2)、(5, 12, 2)；RGV 操作时间To=10 s及车辆进入车厅检查时间分别固定为10 s、30 s。图7为不同待命位策略立体车库运行效率指标对比图，横轴均表示1 d 中以7:00 为0 时刻每间隔1 h 至23:00 间对应时间段，其中，图7(a)纵轴表示顾客平均等待时间指标，图7(b)、(c)、(d)纵轴分别表示RGV 平均服务时间、平均能耗与平均利用率指标。观察图4和图7，随着时间的增加，任务类型由存车逐渐变为取车的过程中，顾客平均等待时间、RGV 平均服务时间及平均能耗效率指标表现出逐渐增加的趋势，RGV 平均利用率指标表现出先增加后减小的趋势。如图7中第9 个时间段，呈现取车顾客达到高峰，存车顾客较少，RGV对应复合作业命令少，因此在原地待命策略下RGV 平均服务时间、能耗及利用率较高。计算1 d 中各待命策略不同均值效率指标如表1所示。

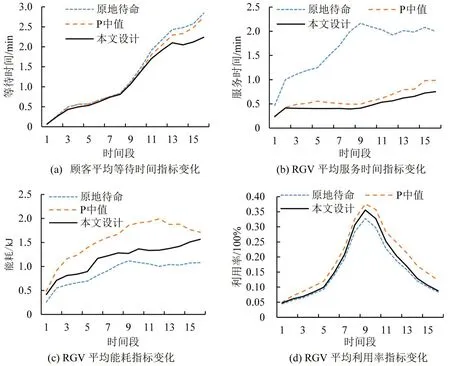
图7 不同待命位策略立体车库运行效率指标对比Fig.7 Comparison of operating efficiency index of stereo garage with different dwell point strategies

对比表1中3种待命位策略下的车库运行效率指标可得：本文设计待命位策略相较原地待命策略与P 中值模型待命策略的顾客平均等待时间分别降低了12.9%和9.2%；RGV平均服务时间分别降低了70.5%和19.2%；RGV 平均能耗较原地待命策略增加32.2%，较P 中值模型待命位策略降低了25.6%；RGV 平均利用率较原地待命策略增加7.8%，较P中值模型待命位策略降低13.5%。此外，由顾客平均等待时间、RGV 平均利用率指标可以看出，该车库客流量较少，顾客RGV利用率水平不高。为探究不同到达率水平对各待命位策略的影响，以得到各待命位策略的适用范围。分别取顾客平均到达间隔时间λ={2,4,6,8,10} min 的泊松流作为顾客源，其他余参数不变，对该车库运行进行模拟仿真，仿真100次下各效率指标结果的均值作为1 d 中对应各运行效率指标值，对比结果如表2所示。

表1 不同待命位策略下立体车库运行效率指标Table 1 Operation efficiency index of stereo garage under different standby position strategies

根据表2分析各待命位策略不同顾客平均到达间隔时间下的各运行效率指标均值变化，图8(a)、(b)、(c)、(d)分别表示顾客平均等待时间均值、RGV平均服务时间均值、RGV平均能耗均值、平均利用率均值随顾客平均到达间隔时间的变化。

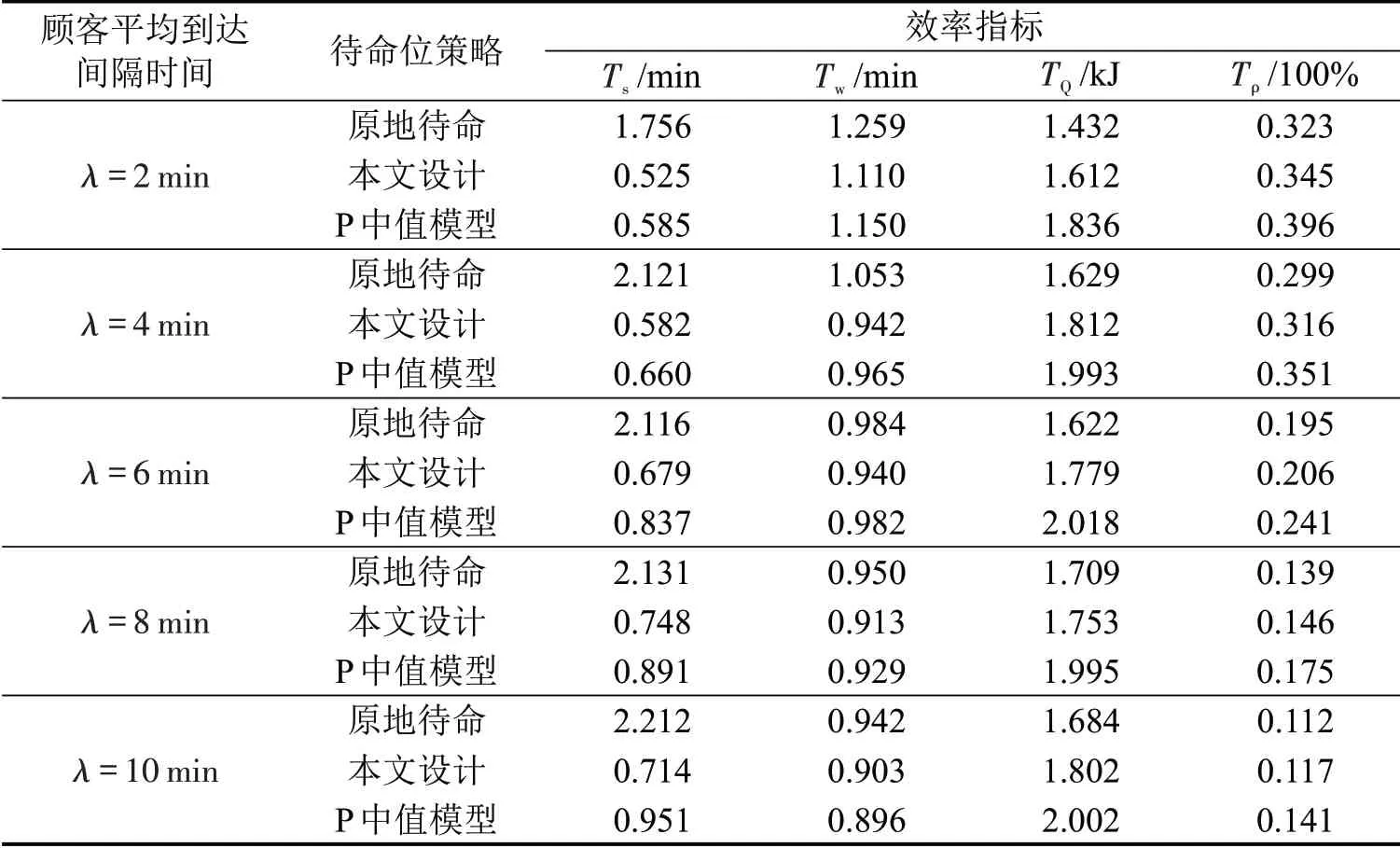
表2 不同顾客到达率下的车库运行仿真结果Table 2 Garage operation simulation results under different customer arrival rate

由图8(a)、(d)可知，随顾客到达率水平增加，3种策略顾客平均等待时间均值、RGV 平均利用率均值整体增加，其中，当λ从10 min→8 min 变化中，本文设计与P中值模型策略的顾客平均等待时间均值较原地待命小，且本文设计平均能耗均值减小幅度较P中值与原地待命大，说明顾客到达率较小情况下，本文设计策略的适用性更好。由图8(b)、(c)可知：当λ从8 min→4 min 变化中，本文设计、P中值模型与原地待命策略的平均能耗均值减少率分别约为4.7%、-3.4%、0.1%，平均服务时间均值减少率分别约为22.1%、26%、0.5%，平均等待时间均值变化率增加约3.2%、3.8%、10.8%，在本文设计与P 中值模型顾客平均等待时间均值变化率相差不大的情况下，P中值模型平均能耗均值增长率最小，而平均服务时间均值减少率最大，说明P 中值模型在λ为8～4 min之间的适用性较好。当λ从4 min→2 min 变化中，本文设计、P 中值模型、原地待命的顾客平均等待时间均值增长率分别约为17.9%、25.5%、19.5%，平均服务时间均值减少率分别为9.7%、10.0%、17.2%，平均能耗均值减少率分别约为11.1%、7.9%、12.1%，平均利用率均值增长率分别约为8.7%、12.7%、7.9%，可知原地待命策略在此到达率区间的表现最优，而在本文设计与P中值模型平均服务时间均值减少率相当的情形下，本文设计较P中值模型更优，P中值模型表现最差，说明该结果与实际相符，如文献[2]所言，高系统利用率下将无待命位。随着系统繁忙度增加，3 种策略下的各运行效率指标趋于相等。

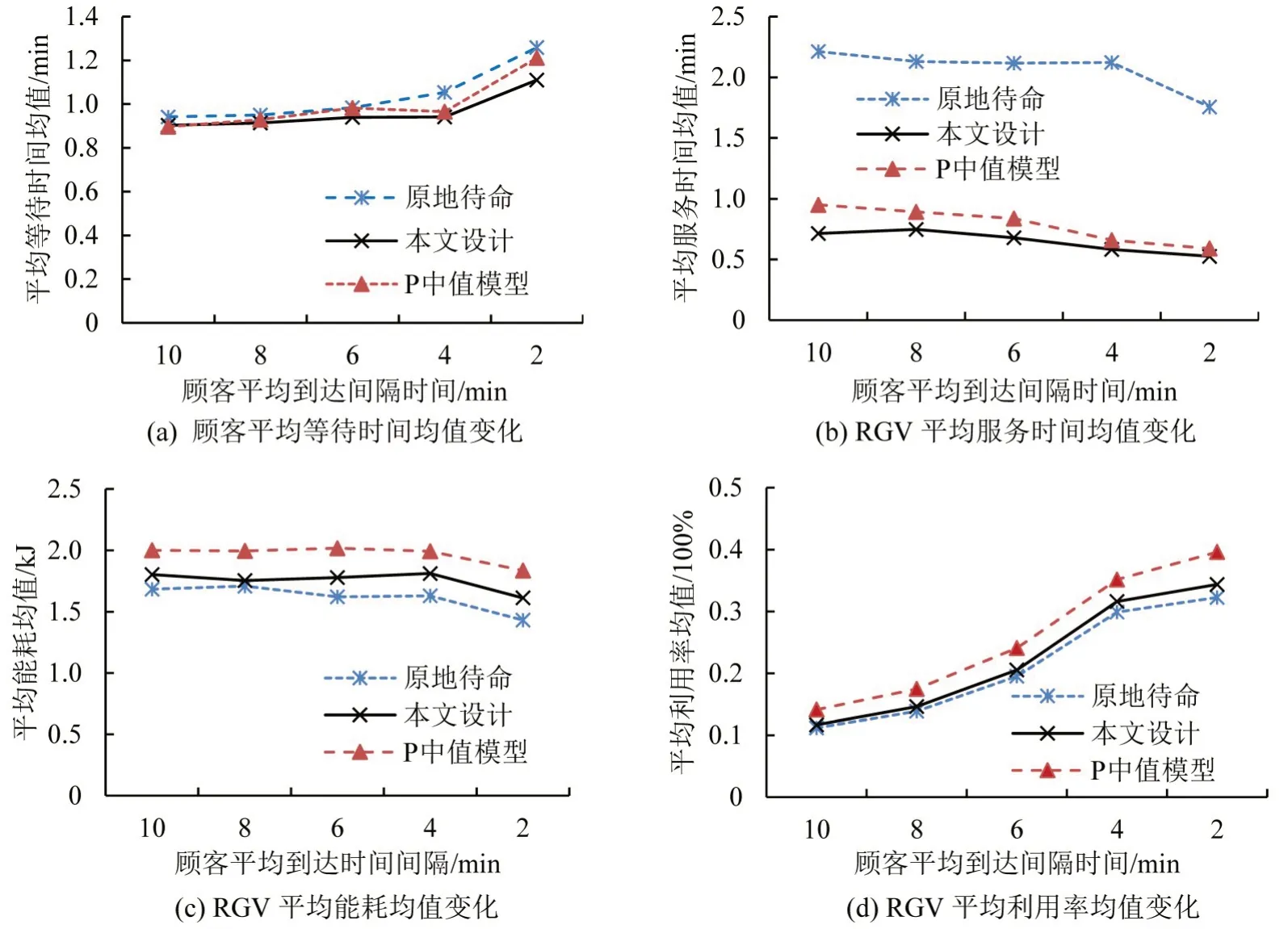
图8 不同到达率下各待命位策略的效率指标均值Fig.8 Average value of efficiency index of each dwell point policy under different arrival rates

5 结论

本文得到的主要结论如下：

(1)对比本文设计与原地待命策略下车库运行仿真结果，通过研究车库顾客到达过程与车辆库内停留时长的拟合，可以较准确地为所研究车库空闲时段下一存、取任务类型的预测提供基础。

(2)对比本文设计与P 中值模型策略下所研究车库运行的仿真结果，表明使用本文设计策略，减小了顾客平均等待时间、RGV平均服务时间、平均能耗及RGV 平均利用率，证明本文设计策略的有效性。

(3)对比仿真结果，分析不同顾客到达率对待命位策略的影响，表明本文设计策略在相同顾客到达率下较另两种策略更优，尤其在顾客到达率较小时，本文设计策略更适用；随着顾客到达率增大到一定值时，相同待命位策略中，P 中值模型相较在低顾客到达率下的表现更优，当顾客到达率足够大时，另两种策略的运行效率指标趋于与原地待命策略相同。

本文基于特定车库的客流时间特性进行预测，未考虑立体车库空间分布特性对预测的影响，在一般性结论方面存在不足；未考虑RGV 动态运行过程中“阻塞”“死锁”对待命位策略设计的影响。后续可在本文基础上结合顾客泊车的时空特性对车库客流及顾客泊车特性深入分析，并考虑RGV 动态运行中RGV避让位置对待命位置选择的影响。