时间依赖型绿色车辆路径问题研究

珠兰，马潇，刘卓凡

（西安邮电大学，现代邮政学院，西安 710061）

0 引言

随着环境污染与能源危机的加剧，以绿色可持续发展理念为导向的低排放、低能耗发展模式成为总体趋势。目前，交通运输已成为全球最重要的温室气体排放源之一，交通拥堵也成为影响城市运输绿色化发展的重要因素。拥堵时段低速行驶的车辆不仅造成更高的温室气体排放，还导致了运输效率的降低和运输时间的不可预测。物流企业作为交通运输行业的重要主体，其运作过程的合理性与社会的可持续发展息息相关。因此，不良交通状况下运输过程的绿色化，是物流运输企业在路径规划阶段需要考虑的重要因素。

运输企业的路径规划问题通常被抽象为车辆路径问题(Vehicle Routing Problem，VRP)进行研究。随着运输导致的环境问题日益严重，考虑温室气体排放等环境要素的绿色车辆路径问题(GVRP)成为研究热点。车辆燃油消耗量、全球变暖潜能值(GWP)[1]、碳排放等价成本等，是常见的温室气体排放的度量指标。由于车辆的燃油消耗量与温室气体排放量直接相关，燃油消耗量被认为是运输过程绿色化的重要指标。此外，由于车辆的燃油消耗量同时受车速、载重、发动机性能等多重因素影响，因此，学者通过一系列燃油消耗模型准确估计运输车辆产生的环境影响。污染-路径问题(Pollution Routing Problem，PRP)[2]由LAPORTE 团队提出，基于综合模式排放模型计算车辆的燃油消耗，分析燃油消耗量与车辆路径选择间的关系，实现环境污染问题与经典VRP 的深度融合，并提出一种改进的大邻域搜索算法求解该问题[3]。在此基础上，他们又将PRP 拓展到最小化油耗和旅行时间的多目标情形[4]。BRAVO M.等[5]研究了考虑同时取、送货情形的多目标PRP，并设计进化算法进行求解。QIU R.等[6]研究了基于碳定价倡议的双层PRP 模型，分析了碳定价策略与企业车辆路径决策间的关系，并设计粒子群算法解决该问题。上述基于燃油消耗的GVRP相关研究中，并没有考虑交通状况对车辆行驶速度、运行时间、燃油消耗以及运输成本的一系列影响，实际中，外在交通状况是随着不同时间段而变化的。

出于这种研究需求，学者开始研究时间依赖型绿色车辆路径问题(TDGVRP)。交通拥堵是时间依赖型路径问题的一个体现，FRANCESCHETTI 等[7]在最小化油耗的车辆路径问题中，考虑了拥堵时段的出发时间优化问题和顺畅时段的速度优化，但模型中仅设定交通拥堵和交通顺畅两个连续时段的旅行时间分段函数。范厚明[8]研究了客户需求模糊且有时间窗约束的TDGVRP，针对不同时间段道路的交通情况，采用Ichoua速度时间依赖函数表征车辆的行驶速度，依据可信性理论构建模糊机会约束优化模型处理客户点模糊需求，并设计自适应大规模邻域搜索算法(ALNS)对其求解。GMIRA M. 等[9]研究1 条路段上存在多条路径的情形下，不同交通状况下的路径选择问题，定义了基于交通状况的速度函数。上述研究考虑交通状况影响下的绿色车辆路径问题，多从速度优化的角度开展研究，而通过优化车辆各节点出发时间的研究还十分有限。

综上，本文以城市配送系统为对象，研究时变交通状况下考虑车辆油耗的车辆路径问题。构建一个时间依赖型绿色车辆路径(TD-GVRP)模型，模型最小化包括燃油消耗、驾驶员劳动和车辆使用折损成本的总成本，定义了允许车辆在节点处等待的情形，通过优化车辆在各节点处的出发时间，以规避拥堵时段并寻求最优路径方案，并设计基于RSM 参数调整的遗传算法求解模型，通过PRPLIB数据库中的算例验证本文所提模型和算法的优势。

1 问题描述

研究的问题描述如下：配送中心的车辆为城市中不同的客户点进行配送，高峰时段的交通拥堵影响车辆运行速度，从而影响车辆的旅行时间和燃油消耗情况；此外，不同路径的选择也将对车辆的旅行时间和燃油消耗产生影响。本文旨在寻求时变交通状况下使得车辆运行总成本最低的路径以及路径上各节点处车辆的出发时间。建模基于如下假设：(1)配送中心所有车辆为有固定容量限制的同质车队；(2)服务期间，车辆发动机关闭，无燃料消耗；(3)拥堵状况以平均速度表示，车辆在途过程中不允许停留。

1.1 旅行时间模型

研究的TD-GVRP问题的时间依赖性主要表现在：不同交通状况下车辆运行速度不同，因而，在不同出发时间对应的旅行时间也不同，即旅行时间是基于出发时间的连续分段函数。出发时间-旅行时间函数的获得过程为：首先，根据路段上时变的车流速度绘制路段上的出发时间-速度函数图；然后，根据路段长度、某一车流速度持续的时间等数据，计算各出发时间对应的总旅行时间；最后，绘制出发时间-旅行时间函数图。由于某一出发时间对应的总旅行时间可能覆盖多个运行速度，因此，旅行时间函数的斜率变化点与速度变化点并不对应。以旅行时间斜率的变化点作为各时间段的分界点，记M={m|m=1,2,…} 为时间段集合；为旅行时间函数斜率变化点；为节点(i,j)间第m个时间段；为时刻出发对应的旅行时间。则在出发时间时间段内的旅行时间曲线的斜率为，该时间段内任何出发时间点对应的旅行时间可通过旅行时间函数的斜率求出，如图1所示。

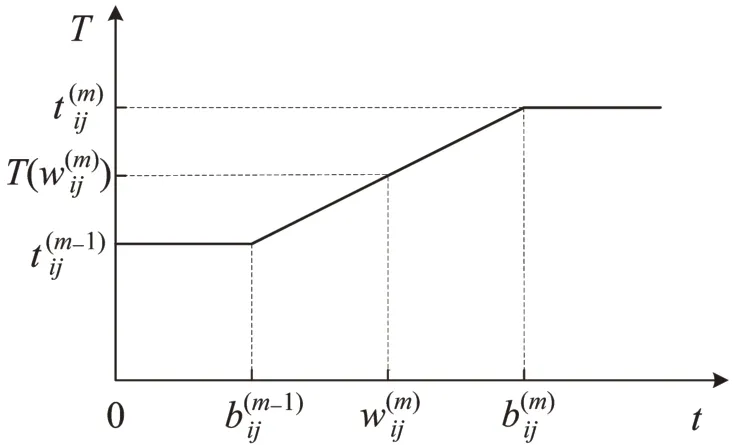
图1 旅行时间计算示意Fig.1 Calculation of travelling time

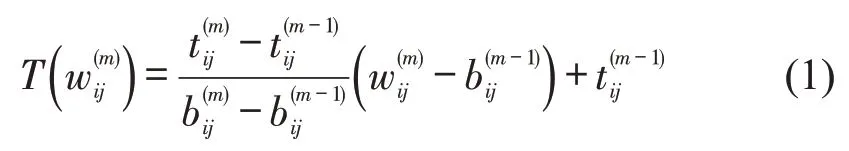
1.2 燃油消耗模型

本文采用综合模式排放模型(CMEM)计算运输车辆的燃油消耗量。经简化，车辆以恒定速度v(m·s-1)和载重l(kg)运行距离d(m)时的总燃油消耗量F为

由式(2)可知，燃油消耗量取决于3 方面，即发动机性能、运行速度和车辆载重。

2 TD-GVRP模型构建

2.1 符号说明

本文模型中涉及的符号说明如表1所示。

表1 符号说明Table 1 Notations description

2.2 模型表达

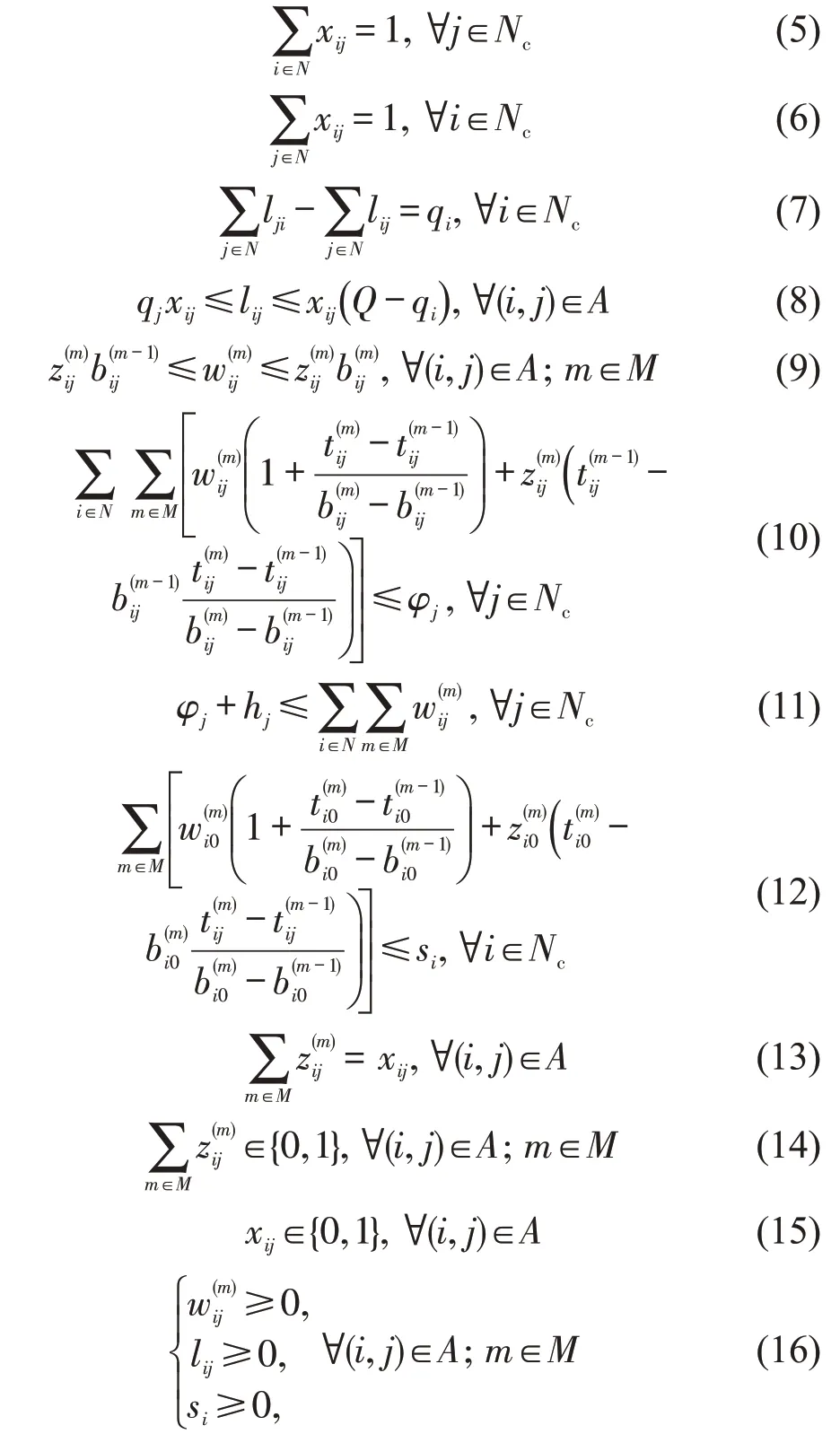
式(3)为车辆总旅行成本最小，其中，前3 项分别为与车辆发动机、车辆行驶速度、车辆负载相关的燃油消耗成本；后2项分别为驾驶员劳动成本和车辆折损成本。式(4)为共有K辆车离开配送中心。式(5)和式(6)保证每个客户节点只被访问1次。式(7)定义了弧上的流量平衡。式(8)为车辆容量约束。式(9)规定了车辆的离开时间。式(10)和式(11)表示车辆在服务结束后可以在客户点等待且无时间限制，当允许等待但对等待时间有限制时，以式(17)代替式(10)和式(11)。式(12)用于计算车辆返回配送中心前的总旅行时间。式(13)为出发时间变量与弧遍历变量之间的关系。式(14)～式(16)为变量的属性约束。

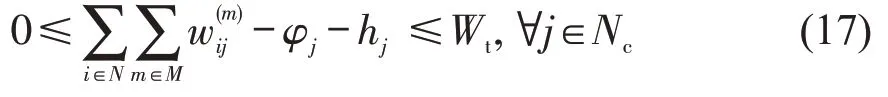
3 基于RSM参数调整的嵌套遗传算法

本文设计了遗传算法(GA)求解模型。由于启发式算法的性能对其参数设置十分敏感，利用基于响应面法(Response Surface Methodology，RSM)的试验设计方法调试影响遗传算法性能的关键参数。

3.1 算法概述

算法包含两个优化因子：车辆路径和各节点处的出发时间，在外部GA 算法优化车辆路径的框架下，通过一个内部GA算法优化当前路径序列的出发时间。算法流程如图2和图3所示。

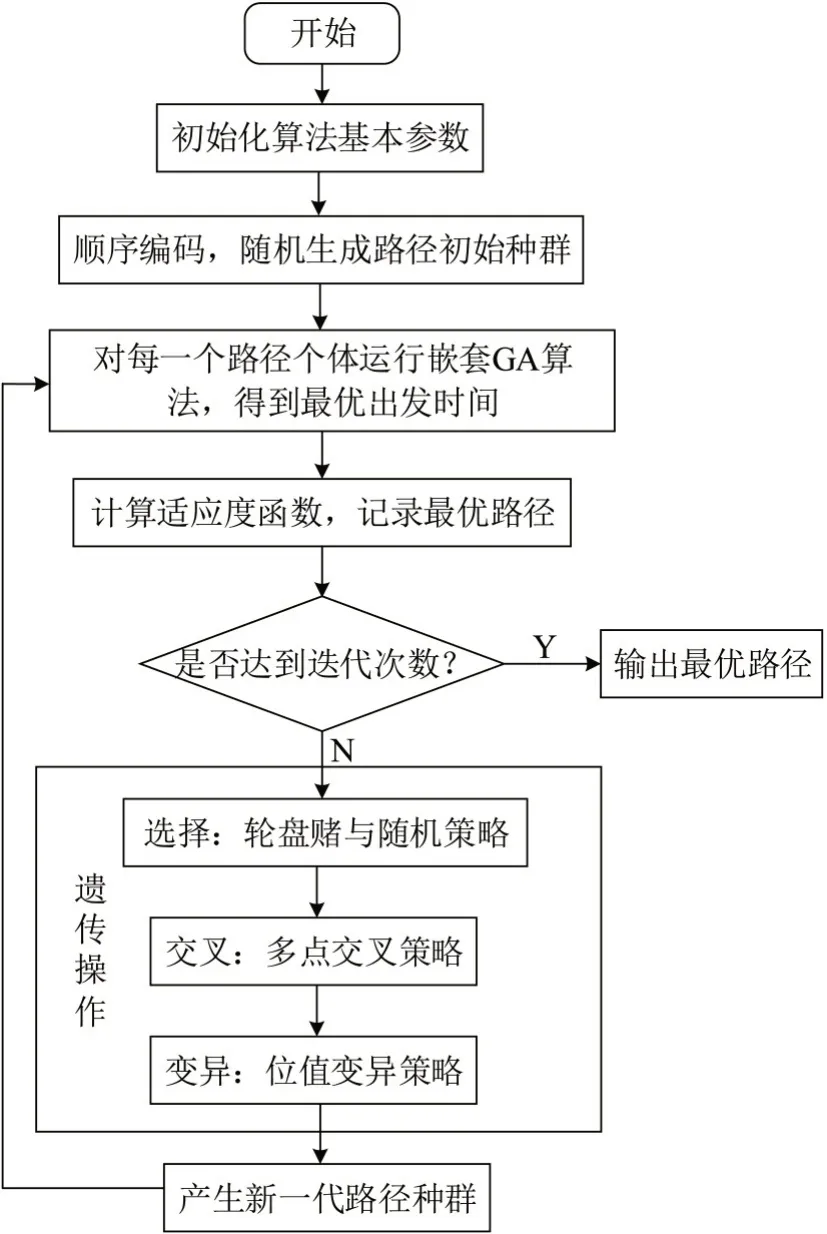
图2 外部GA算法流程Fig.2 Flowchart of exterior GA

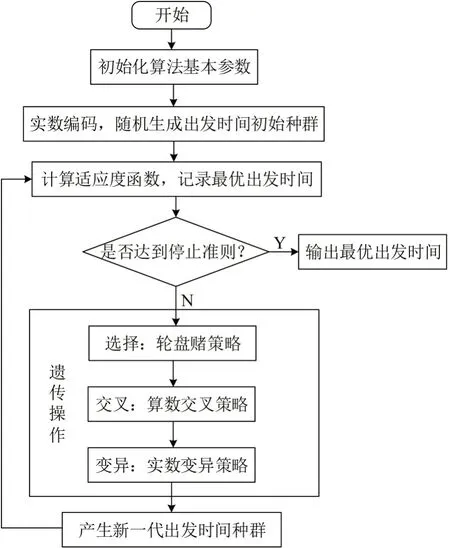
图3 内部GA算法流程Fig.3 Flowchart of interior GA

(1)外部GA算法

各节点按0,1,2,3,…,N顺序编码，其中，0为配送中心，N为客户点的数量。随机生成Ps个0～N的随机序列构建路径初始种群。对于本文最小化问题，选取目标函数的倒数作为适应度函数，当某条路径上的总负载超过车辆容量，则为对应的目标函数乘以一个惩罚系数，降低适应度函数。选择操作中，基于轮盘赌策略选择父代P（1），父代P（2）随机选取。交叉操作基于多点交叉算子进行，过程如下：在P（1）中随机选择3 个基因，将其复制到子代相同基因位上；去掉P（2）中与P（1）所选基因值相同的基因；将P（2）中剩余基因按顺序依次填入子代O（1）中，如果遇到某一基因位上已经存在基因值，则跳过该基因位继续填入下一个位置。变异操作基于位值变异，以码长为上限随机确定两个不同点，互换基因，通过预设最大迭代次数作为算法终止规则。以10个客户节点的问题为例，外部GA算法交叉算子如图4所示。

图4 外部GA算法交叉算子示意Fig.4 Crossover operator of exterior GA

(2)内部GA算法

当前路径序列的出发时间通过实数编码实现。随机生成PS（1）个染色体长度为N+K的初始种群，其中，K为车辆数；选取目标函数的倒数作为适应度函数；选择操作中两父代P（1）和P（2）均通过轮盘赌策略选出；采用基于算数交叉的算子进行交叉操作，子代O（1）和O（2）每一个基因位上的值为

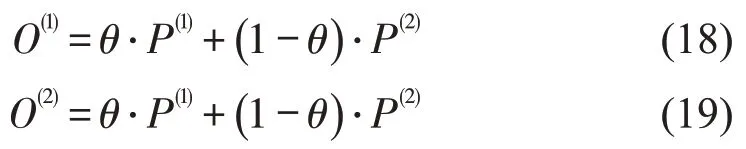
式中：实数θ∈[0 ,1] 为乘子；变异操作采用实数变异法，在父代上随机选择1个基因位，将定义域内的1个随机数赋值给该位置；算法停止通过当前迭代最优值与前1次最优值的差值来控制，当连续n次(本文为30 次)前后迭代最优值的差值小于10-6，则停止运算返回最优值。

3.2 RSM概述

响应面法(RSM)是通过近似构造1个显函数得到复杂系统输入(变量)与输出(响应)之间关系的方法，通过近似构造1个显函数构造待测量的全局逼近。如果当前输入变量的水平接近响应面的最优位置，一阶逼近模型即可准确拟合响应曲面，当拟合区域存在弯曲，则必须用更高阶的二阶模型逼近。复合中心设计(CCD)是拟合二阶模型非常有效的一类设计。本文选取外部GA算法的4个关键参数：种群规模Ps、进化代数n、交叉率Pc以及变异率Pm作为优化因子，以本文算法的目标函数作为响应量，分析不同参数组合下的响应情况，得到响应与输入变量之间的拟合关系，确定本文算法在求解模型时的最佳参数取值。

4 应用与分析

本文提出的模型和算法应用于一组城市配送系统算例，算例来源于DEMIR 等[3]提出的污染-路径问题实验数据库PRPLIB，该数据库包含：10，15，20，25，50，75，100，200 个客户节点的8 组算例，每组又包含20个不同算例，例如，算例UK25_01表示节点规模为25 的算例组中的第1 组算例。本算例考虑2辆车在拥堵-非拥堵两阶段下进行配送活动的情形。研究时间段设为b=5 h；高峰拥堵持续时间a=2 h；车辆在拥堵时段的速度vc=20 km·h-1；其余时段的速度vf=40 km·h-1。车辆相关参数取自江淮HFC1082KD 厢式载货车。算例通过CPLEX 12.5 求解器和基于MATLAB 的GA 算法求解。其中，CPLEX求解器的求解时间上限设为3 h。所有试验均在一台Core i5处理器，内存2.2 GHZ个人电脑上完成。出发时间-速度关系如图5所示。对应的旅行时间函数如图6所示。

图5 出发时间-速度关系Fig.5 Relationship between departure time and speed

图6 出发时间-旅行时间关系Fig.6 Relationship between departure time and traveling time

4.1 算法参数调试

在本文RSM试验中，因子Ps、n、Pc、Pm分别以编码符号x1,x2,x3,x4表示，取值范围以及水平划分如表2所示。

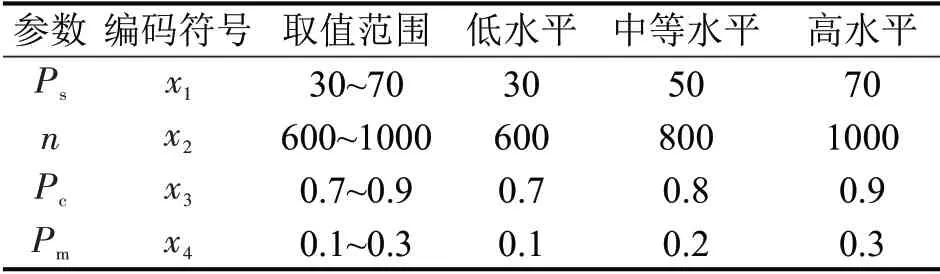
表2 输入变量的范围与水平划分Table 2 Range and levels of input variables

本文选取的中心复合设计方案包含8 个分式因子试验点、8个坐标轴试验点和4个中心试验点，共运行20 组试验。试验算例选取UK25 系列的10组算例，求得各组试验方案的平均响应值。然后，由Design Expert 软件在5%的置信水平下进行试验，得到二阶回归拟合模型为

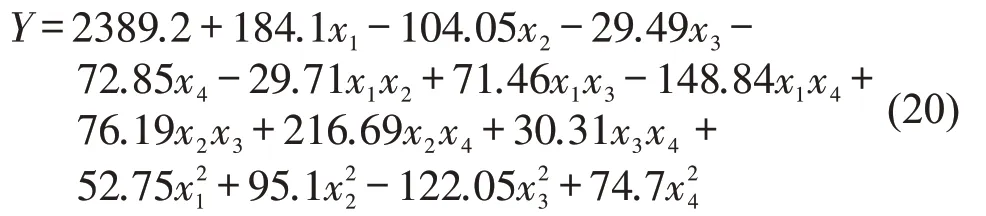
通过Lingo 软件求解二阶多元回归模型，最小化响应值Y，得到本文GA 算法的最优参数组合为：Ps=50、n=800、Pc=0.7、Pm=0.1。

4.2 算法性能比较

为检验本文GA 算法的求解性能，本文分别通过CPLEX 求解器和GA 算法求解算例UK10～200，分别得出目标函数值Z1、求解时间St、不可行解所占比例pf以及解的改善百分比pm，结果以每组10个算例的平均结果给出。其中，求解质量的改善百分比由(CPLEX 解-GA 解)/CPLEX 解求得，用以表示GA 相对CPLEX 的求解精度。CPLEX 与GA 求解结果比较如表3所示。

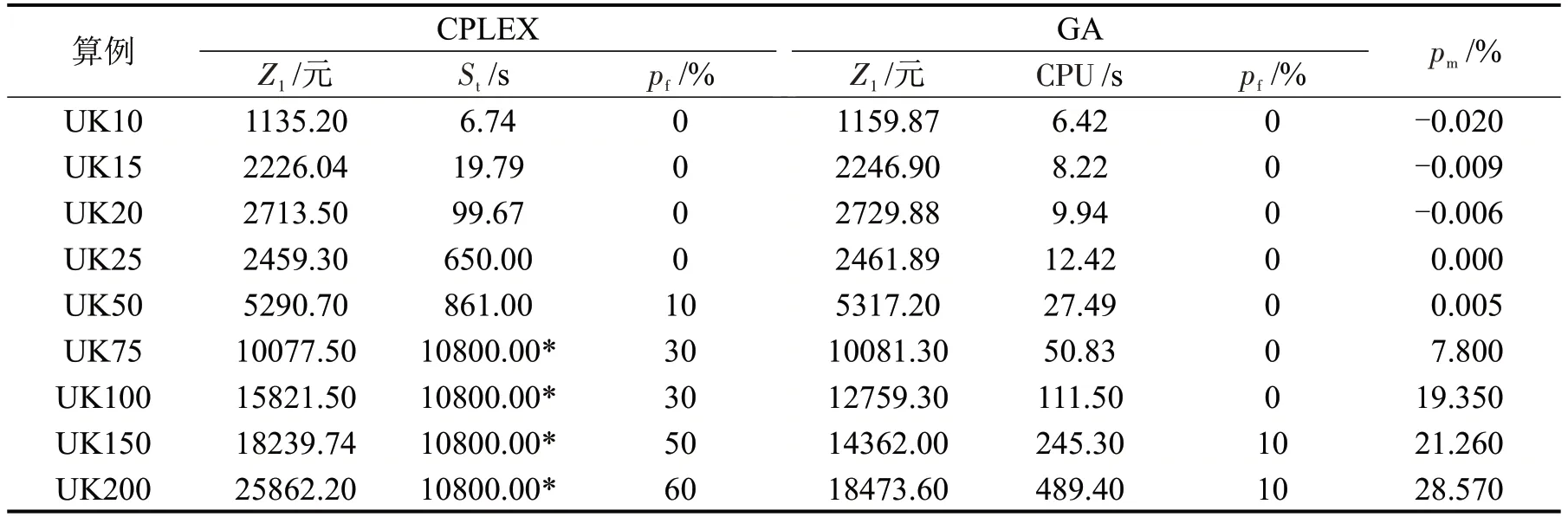
表3 CPLEX与GA求解结果比较Table 3 Results comparison of CPLEX and GA

由表3可知，CPLEX 在包含10 个节点的算例中可以求得全局最优；而当节点规模上升至50时，10个算例中的1个不能求得可行解；当节点规模上升至100时，所有算例无法在时间限制内取得最优解，且10个算例中的3个没有在3 h内找到可行解；当节点规模上升至200 时，在时间限制内，CPLEX求得的不可行解的比例达到60%。对不同规模算例，GA均能在短时间求出高质量可行解，且随着算例规模的增大，其相对于CPLEX 的求解质量改善程度也在明显增加，尤其是当CPLEX 无法在时间限制内求得最优解时，在200个客户节点的大规模算例中，改善比例高达28.57%。

此外，在求解速度方面，GA 明显优于CPLEX。对于10 个节点的小规模算例，两者求解时间相近，随后，求解时间的差距随着算例规模的增加而显著增加；对于50个节点的中等规模算例，GA 平均仅需27.49 s，而CPLEX 则需要861 s；对于100个节点的大规模算例，GA平均仅需111.5 s。由此说明，本文提出的基于RSM参数调整的GA算法可以有效求解本文提出的TD-GVRP模型。

4.3 不同目标的影响分析

本文以GA 求解UK10_01、UK15_01 和UK20_013 个算例的结果，说明不同目标对决策方案的影响。除总成本目标外，设置3个决策者较为关心的目标，分别是燃油消耗最小化Z2，传统VRP目标总旅行时间最小化Z3和总旅行距离最小化Z4，即

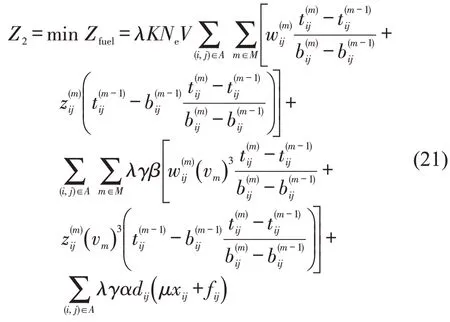
不同目标下，各决策要素的值包括：总成本Tc，总CO2排放Te、总旅行行时间Tt和总旅行距离Td，如表4所示。表中所有值均以最小化燃油消耗目标Z2求得的值为基准进行标准化。

本文设置的4个目标函数中，与燃油消耗有关的目标函数为Z1和Z2。由表4可知，以本文TDGVRP模型目标函数Z1求得的燃油消耗仅比Z2结果高出4.9%，传统VRP目标Z3和Z4求得的平均燃油消耗则分别比Z2结果高出了65.78%和13.64%。由此可知，目标函数中燃油消耗因素的引入，可以大大降低决策方案对应的燃油消耗。此外，Z3结果显示，较短的旅行时间将以较高的成本和CO2排放为代价。

表4 不同目标对各决策要素的求解结果Table 4 Decision factors under different objectives

4.4 拥堵时长影响分析

为研究拥堵时长对决策要素的影响，本文通过求解UK20 系列算例，进行总燃油消耗和总旅行时间对于拥堵时长参数的敏感度分析。以0.25 h 为步长，当拥堵分别持续0～2 h，10个算例的平均燃油消耗量和平均旅行时间的变化如图7所示。

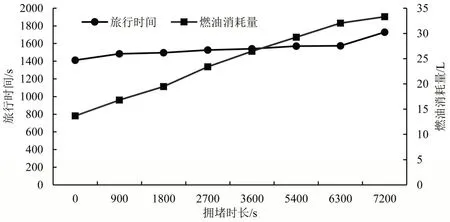
图7 拥堵时长参数的敏感度分析Fig.7 Sensitivity analysis of congestion parameter

由图7可知，当不允许车辆在客户处停留等待时，拥堵持续的时间越长，将导致越高的燃油消耗量和越长的旅行时间。这是由于较长的拥堵时间导致车辆总行驶周期内低速行驶比例增大。

4.5 等待时间影响分析

为研究等待时间Wt对决策要素的影响，即不同的出发时间对成本Tc、燃油消耗Te和旅行时间Tt的影响，对比并分析不同等待时间约束下的结果如表5所示。结果由UK20 系列中10 组算例的平均值给出。

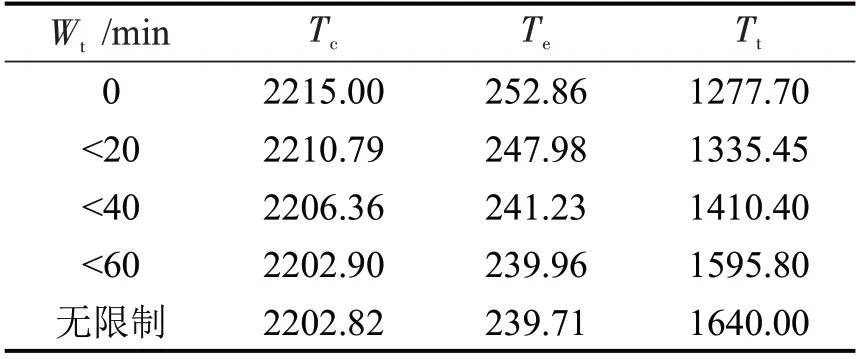
表5 不同等待时间对各决策要素的求解结果Table 5 Decision factors under different waiting times

表5结果显示，与不允许等待的情形相比，等待时间无限制的情形可节省5.2%的燃油消耗，总成本下降0.55%。由于总旅行时间中引入等待时间，总旅行时间增长了28.35%。由此可见，如果允许在客户处等待，选择合适时间出发以规避拥堵，可以在一定程度上降低燃油消耗和总成本。然而，在总成本降低并不明显的情况下增加总运营时间，从运营角度分析可能并不是较好的方案，但却能达到较客观的节能环保效果。

5 结论

本文得到的主要结论如下：

(1)通过不同目标的影响分析可知，与传统VRP 问题相比，目标函数中引入燃油消耗要素，可以有效降低决策方案的燃油消耗量。

(2)对拥堵时长参数的敏感度分析结果显示，较长时间的拥堵将导致更长的旅行时间和更多的燃油消耗。

(3)通过等待时间影响分析可知，当允许车辆在客户处等待并选择合适时间出发，最多可节省5.2%的燃油消耗和0.55%的总成本。