甩挂运输模式下新增运输任务的干扰管理模型

王清斌，于江宁，郑建风

（大连海事大学，交通运输工程学院，辽宁大连 116026）

0 引言

循环甩挂是用循环调度的方法来组织封闭回路上的甩挂作业，以牵引车为循环调度对象，挂车为需要装载或卸载的货物。客户点为装卸作业点，也用于收取货物、暂时停靠和拖挂车辆。

在这个作业组织过程中，甩挂运输车辆路径问题(Truck and Trailer Routing Problem，TTRP)是传统车辆路径问题的衍生问题。甩挂运输组织者会根据顾客的配送时间要求制定每天的车辆路径调度方案。但在实际中，经常会出现诸如临时插单、装卸点备货时间调整使得原属于下一天的任务提前至当天，而产生新增运输任务的情况，这会对当天的调度方案造成干扰，导致配送车辆可能无法按照原方案服务客户。

针对新增运输任务的干扰问题，一些学者运用全局重调度方法进行处理。李兵[1]提出引入虚拟任务点将动态路径规划问题转化为普通静态问题，运用改进的节约法对问题进行求解。Tasan[2]等和Zhang[3]等对动态路径规划问题进行了重新优化，但没有将原方案考虑在内。然而当新增需求过于频繁时，路径的实时优化无法实现。葛显龙等[4]通过将配送时间划分时间段，将动态需求过程转化为多个瞬时静态子过程进行求解，并设计云遗传算法实时优化配送方案。饶卫振[5]针对新客户出现的动态事件，将动态车辆路径问题转化为多车型开放式车辆路径问题，再进一步转化为多个能力约束车辆路径问题，在此基础上建立动态车辆路径模型，并提出两阶段算法。张文博[6]提出两阶段建模，采用模拟退火算法得到实时优化后的车辆路径方案。但由于其运用的是全局重调度法会造成新方案时间和路径与原方案偏离较大，对系统造成扰动。

从以上学者研究可以看出，全局重调度是以整个系统总费用最低为目标，进行全局优化调整。通过牺牲原运输任务配送时间的及时性和准确性，从而换取整个配送系统的更低的成本变动。在实际甩挂运输中，一个运输任务涉及到装、卸货两点的时间窗变动，时间变动会造成两个客户点的服务体验下降，而物流本身就是一种服务，在提供运输服务的过程中必须考虑客户的服务体验。因此有学者提出运用干扰管理的思想，杨华龙等[7]针对客户时间窗变动情况，设计基于禁忌搜索的调度算法，通过算例证明干扰处理方法优于全局重调度方法。赵亮[8]针对客户需求量和时间窗的变动情况，建立干扰管理模型，优化同时送取货的车辆路径方案。丁秋雷等[9]针对行驶时间延迟情况，从物流配送运营商的视角，在模型创建中引入客户终身价值，构建了扰动较小的配送方案。由此可以看出，基于干扰管理思想的研究可以更好地克服全局重调度方法中存在的问题，但现有的研究多是对传统车辆运输模式下客户时间窗、需求量等因素变动的研究，而对于新增运输任务造成的配送车辆调度问题研究尚少，并且针对甩挂运输的研究还停留在静态车辆路径问题上。

基于上述情况，本文运用干扰管理思想，针对甩挂运输模式下出现新增运输任务的问题，以考虑配送车辆调整、路径偏离和服务时间偏离的广义总成本最小化为目标，对原车辆路径调度方案进行调整，为甩挂运输组织应对新增运输任务的干扰管理提供决策支持。

1 问题描述

本文考虑由一个牵引车车场和多个客户点组成的甩挂运输系统，在配送开始前，以运输成本最低为目标生成初始方案并安排牵引车进行配送。本文将干扰发生时车辆正在服务的客户点视为已完成客户点，客户需求发生的变动视为新增运输任务，干扰发生时，基于当前系统状态，运用干扰管理思想生成新的车辆路径方案，以使干扰对原方案造成的扰动(广义总费用偏离)最小。

2 扰动主体的度量分析

顾客下达配送订单后，甩挂运输组织者根据顾客的配送时间要求以1 d为一个调度期生成车辆运输路径方案，由于在实际运输过程中存在新增运输任务，本文以660 min 为接受新增运输任务的干扰时刻，若新增运输信息出现在该时刻以后，该任务将进入下一个调度期进行配送。

当客户需求发生变动后，系统需要进行扰动辨识，判断干扰事件是否对原方案造成干扰，若没有产生干扰，则按照原方案行驶。若产生了干扰，则系统要在最短的时间内，基于干扰管理思想，生成广义总费用偏离最小的车辆路径方案。广义总费用偏离包含4 方面内容：(1)由于新派车产生的费用；(2)由于在途车辆运输距离的增减而引起费用的增减；(3)对服务时间偏离的处理，通过引入时间偏离惩罚系数将时间的偏离转化为相关费用；(4)由于不能接受新增任务而放弃客户的惩罚成本。

在路径偏离上，仅由于牵引车行驶路径的偏离产生的与路径距离有关的运输成本变化可分为两种情况，如图1所示。设原路径为rijk(表示空挂从i到j的路径)，第1 种情况是牵引车完成任务m，空挂从i出发前就已知要改变原路线，先去服务新任务m′再去服务m+1，如图1(a)所示，设T表示干扰发生时刻，Li表示车辆从i离开的时间，则这种情况可以表示为T ＜Li，这时路径的偏离可表示为空挂rijk的减少和空挂rigk、rhjk，重挂rghk的增加；第2种情况是牵引车完成任务m，空挂从i出发后，临时得知需要变更下一个客户点，即车辆是空挂状态驶向下一任务点，此时车辆位置为p，如图1(b)所示，设Sj表示开始服务j的时间，则这种情况可以表示为Li ＜T ＜Sj，这时原路线并没有完全减少，而是与新路线有重合部分空挂ripk，路径的偏离可表示为空挂rpjk的减少和空挂rpgk、rhjk，重挂rghk的增加。当干扰信息发生时车辆若为甩挂运输任务状态，要等到任务结束在进行调整，或在车场派送新的牵引车。

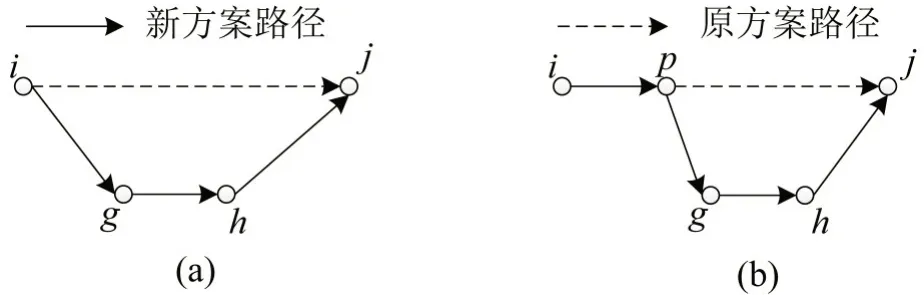
图1 车辆路径偏离情况Fig.1 Deviation of vehicle route

在运输任务的服务时间偏离方面，本文引入时间费用偏离惩罚系数把时间偏离量化成广义时间费用偏离[10]。即调整原车辆调度方案后，若配送车辆到达任务m客户点开始服务时刻，在任务m允许的最早开始服务时刻之前，车辆因等待产生了损失成本，此时，时间偏离惩罚系数记为α；若配送车辆到达任务m客户点开始服务时刻，在任务m允许的最迟开始服务时刻和客户允许的延迟时间Δt之间，则会对客户的满意度造成一定的影响，此时，将时间偏离惩罚系数记为λ；若车辆到达客户点时，该客户的时间窗已经关闭，该车辆不能再对其服务，将惩罚系数定义为一个无穷大的正数M。

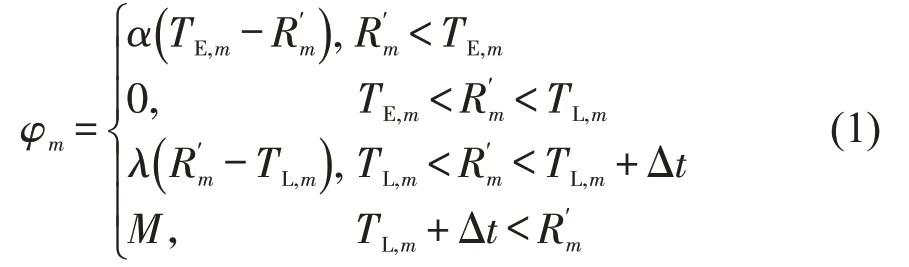
在式(1)的基础上，本文基于干扰管理的思想，需尽可能减少新方案与原方案的差异。因此，加入新方案与原方案中任务开始服务时间的偏离费用，即

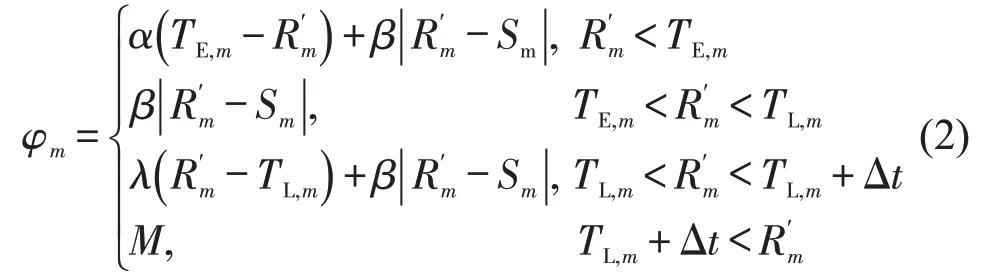
本文从两方面考虑：一方面是基于实际服务时间与时间窗差异，而产生的一个时间窗惩罚成本；另一方面是基于干扰管理的思想，尽量小的扰动，尽快恢复系统正常运行。为尽可能使新方案与原方案之间的偏离程度更小，该计算是判断新方案优劣的一个指标，将任务开始服务时间的偏离转化一个时间偏离惩罚成本，由此构造出广义费用这一概念。本文客户点的时间窗是对牵引车开始服务的时间限制，因此，如果出现牵引车实际到达后的时刻在客户时间窗内，但甩挂作业结束后超过客户允许时间范围，这种情况不会对客户的满意度造成影响，时间惩罚不予以考虑。

3 模型构建

模型中的变量及参数符号定义如下：

T——扰动发生的时刻；

D——客户集合，D={1,2,…,n} ，n为客户点数量；

N——地点集合，N=D⋃{O} ；

O——车场；

K——已使用牵引车数量；

P——待使用牵引车数量(车场剩余)；

p——增派车辆数；

M——甩挂时段内的运输任务总数；

m′——甩挂时段内新增任务数；

M′——扰动发生时原方案为服务任务数；

Cij——从位置i到j的运输成本；

tij——从位置i到j的行驶时间；

C——完成甩挂任务所需要总费用；

C0——每辆牵引车每天出车固定费用(车辆购置费用，维修费用以及驾驶员工资)；

V1——牵引车空挂时行驶速度；

V2——牵引车重挂时行驶速度；

Gk——牵引车k的额定载重；

gk——挂车的空车质量；

gm——任务m运输任务量；

α——若车辆到达任务m客户点时刻，在时间窗之前到达的时间偏离惩罚系数；

λ——若车辆到达任务m客户点时刻，在任务m期望服务截止时间和客户允许的延迟时间Δt之间的时间偏离惩罚系数；

β——若车辆到达任务m客户点时刻，偏离原任务开始时间的时间偏离惩罚系数；

F——放弃一个客户的惩罚费用；

Δt——客户时间容忍度；

M——客户时间窗已经关闭，该车辆再对其服务的时间偏离惩罚系数；

sm——任务m装货点；

rm——任务m卸货点；

Sm——原方案开始服务任务m的时刻；

S'm——新方案开始服务任务m的时刻；

R'm——新方案到达任务m装货点的时刻；

t'kn,s——牵引车k执行第n次运输任务时的开始时刻；

tknmsm+1——牵引车k执行从运输任务m的终到点到运输任务m+1的起始点所需时间；

Sm,s——任务m最迟开始时刻；

Sm,f——任务m结束时刻；

tm——甩挂运输持续时间；

tp——甩挂作业时间；

[TE,m,TL,m]——任务m要求的时间窗；

TE,m——任务m允许的最早开始服务时刻；

TL,m——任务m允许的最迟开始服务时刻；

φm——任务m的时间偏离惩罚费用；

dij——客户i到j的距离；

dpjk——扰动发生后原车辆k从当前位置到客户j的行驶距离；

d1k——扰动发生后车辆k按原方案服务剩余空挂的总行驶距离；

d2k——扰动发生后车辆k按原方案服务剩余重挂的总行驶距离；

——扰动发生后车辆k正在服务任务m的结点；

Pk——扰动发生后车辆k空挂在行驶途中。

扰动后模型为

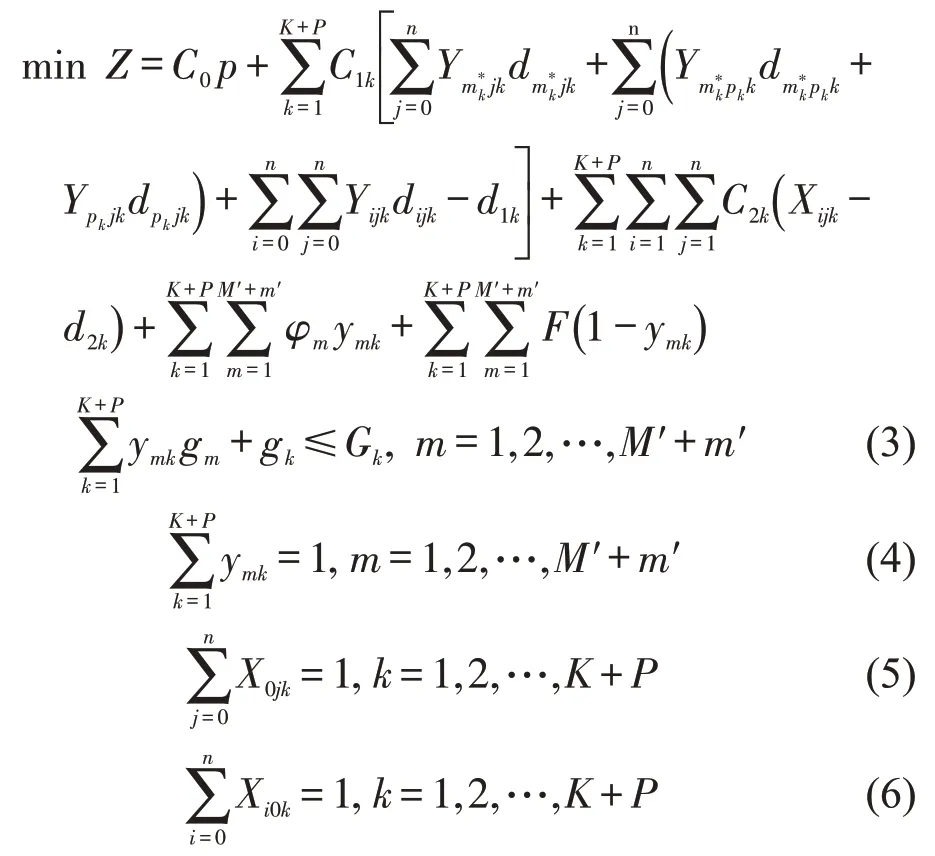
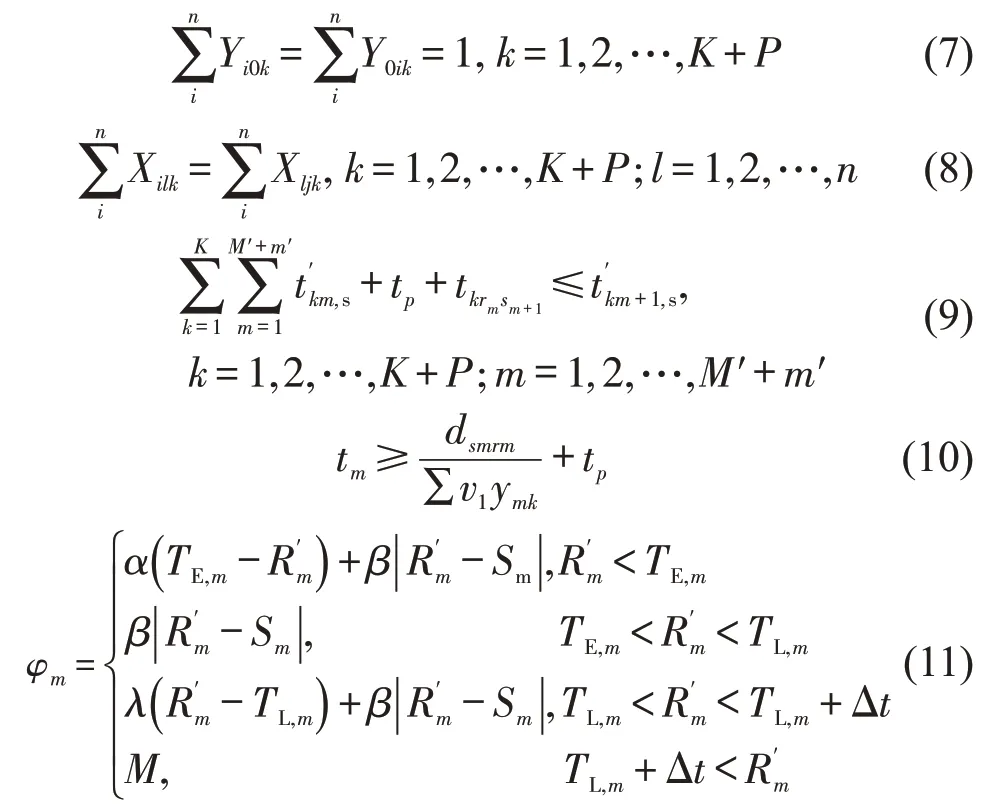
式(3)表示任务m的运输重量与半挂车的重量和不超过牵引车k的最大额定载重量；式(4)表示甩挂运输任务m只能由牵引车k完成；式(5)表示牵引车k从原点出发执行运输任务；式(6)表示牵引车k完成运输任务最终回到原点；式(7)表示出发返回必须是空车；式(8)表示牵引车进入和驶出节点数量相同；式(9)为牵引车执行运输任务被完成的先后次序约束；式(10)表示新方案中执行任务m甩挂运输持续时间；式(11)表示时间偏离惩罚取值

4 算法设计

实际配送过程中，虽然客户会发生需求变动，但并不是所有客户的需求变动都会对原方案造成干扰，如，新增任务的时间窗及路段为原方案中牵引车在该时段空挂行驶的路线，则该变动不会对原方案造成影响，也就不会产生干扰，否则，该变动会对原方案产生干扰。

在配送过程中，原方案是从车场出发回到车场的闭环路径方案，而针对新增运输任务变动路径方案的算法设计，是在调度时刻从各个在途车辆所在虚拟客户点的位置回到车场的路径算法设计，实质是由多点返回到车场。

在实际中，当干扰发生，需要对车辆路径进行调整时，将车辆在途和车辆正在某个客户点等待的情况，都看作是车辆停留在“虚拟客户点”，这样新方案则发生在服务完虚拟客户点之后。本文通过修改虚拟客户点的属性，将多点返回到车场的开环路径转变为闭环路径问题，采用改进的多种群并行遗传算法求解，算法设计整体框架如图2所示。

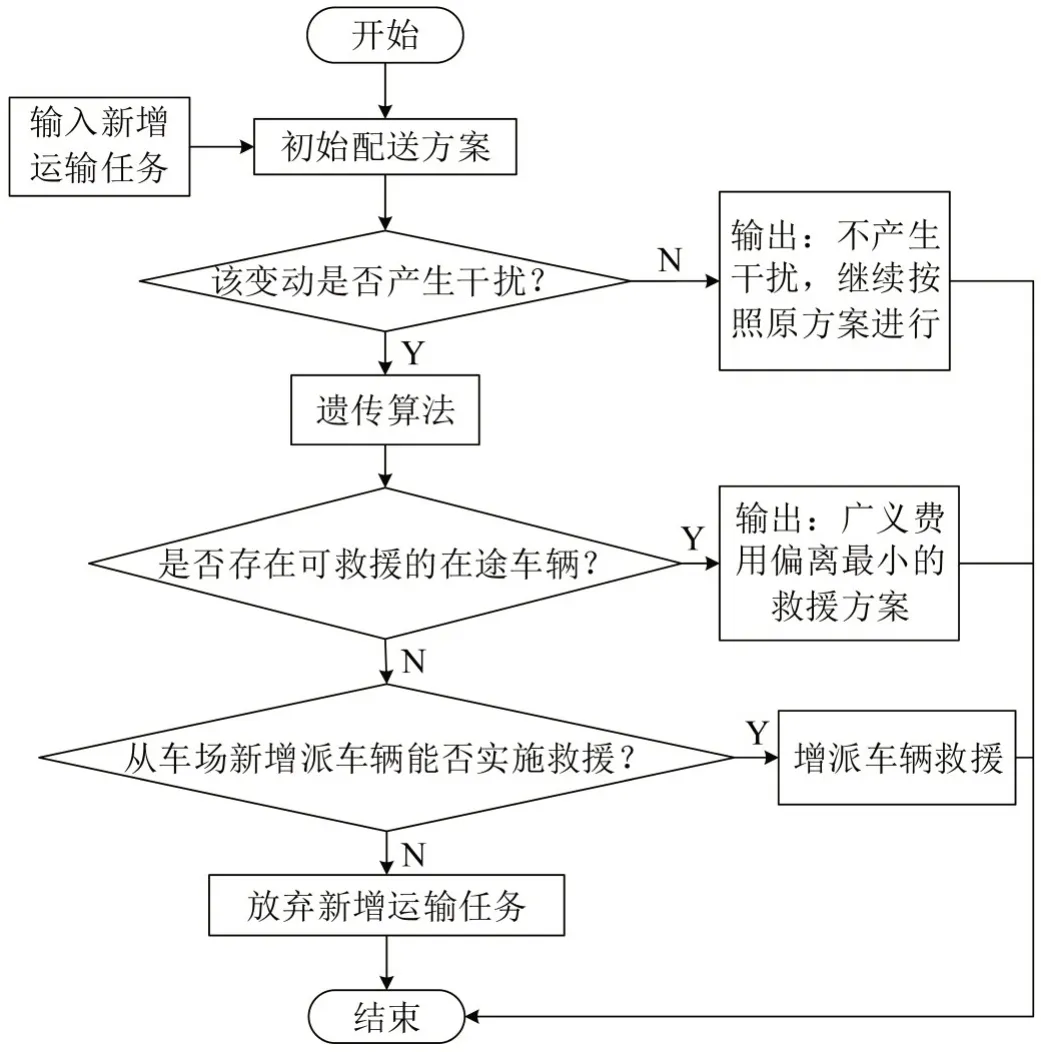
图2 算法设计整体框架Fig.2 Overall framework of algorithm design

本文采用改进的多种群并行遗传算法求解该问题，步骤如下：

Step 1 随机产生指定个体数目的3 个初始种群作为并行算法的子种群。

Step 2 并行计算各子种群中个体的适应度。

Step 3 采用轮盘赌方式并行执行各子算法的选择算子。

Step 4 按交叉概率并行执行各子算法的交叉算子。

Step 5 按变异概率并行执行各子算法的变异算子。

Step 6 在各子种群中优选适应度较好的个体。

Step 7 若满足停止准则，输出结果；否则，转Step 2。

结合虚拟客户点策略的并行遗传算法本身不需要做结构调整，只需要在干扰调度时刻重新对虚拟客户点、新增客户点和原计划未服务客户点信息的重新汇总并在算法中重新对这类客户读取数据。

5 数值验证

为了验证模型和算法的有效性，本文在300 km×300 km 平面采用随机方式选取15 个点，生成40个运输任务。某日甩挂运输系统接到15个客户点的订单，物流配送中心和客户点的坐标如表1所示，运输任务和时间窗信息如表2所示，其中，标号1 表示车场。车场有15 辆牵引车，300 km×300 km平面中重挂行驶速度80 km·h-1，空挂行驶速度100 km·h-1，C1=1.8 元·km-1，C2=3.6 元·km-1，C0=416 元·车-1[11，]α=10 元·min-1，β=1 元·min-1，λ=10 元·min-1，Δt=30 min[12]。

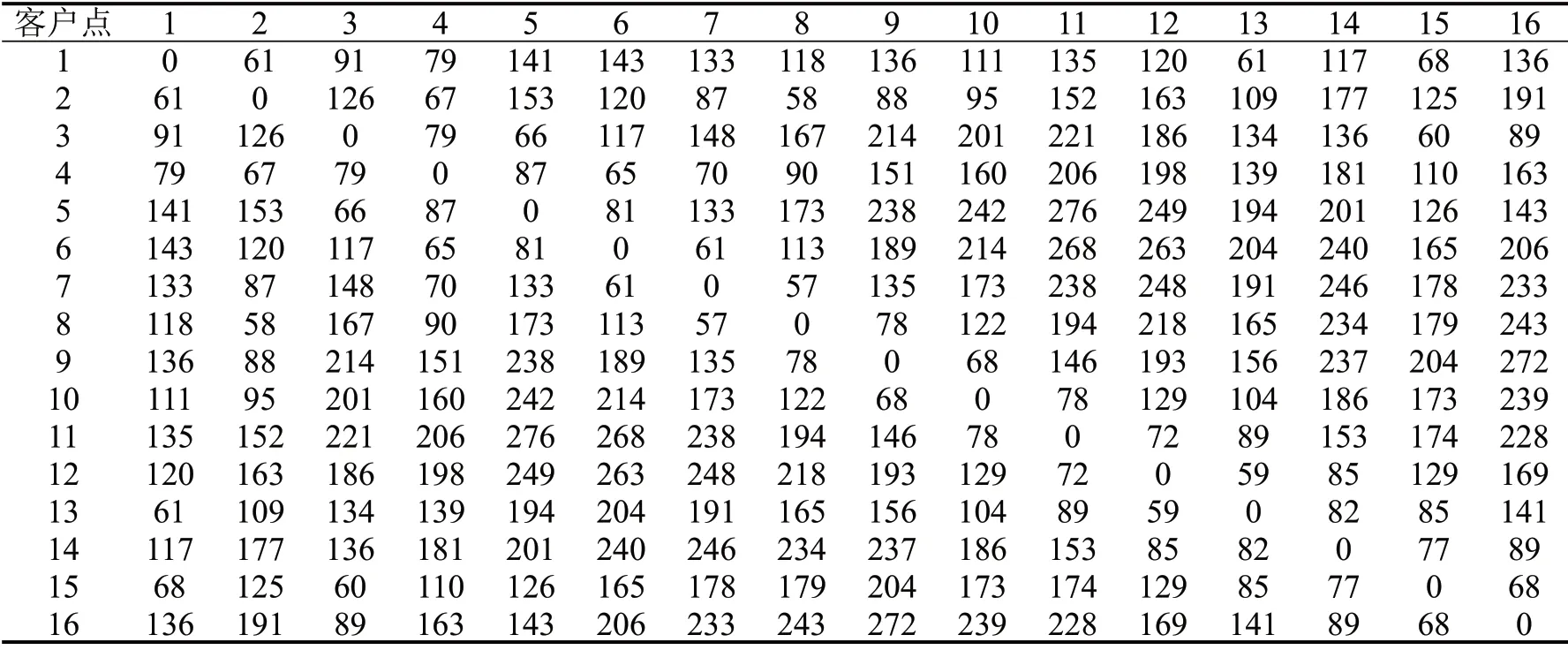
表1 甩挂中心及客户点位置Table 1 Drop and pull center and customer location（km）

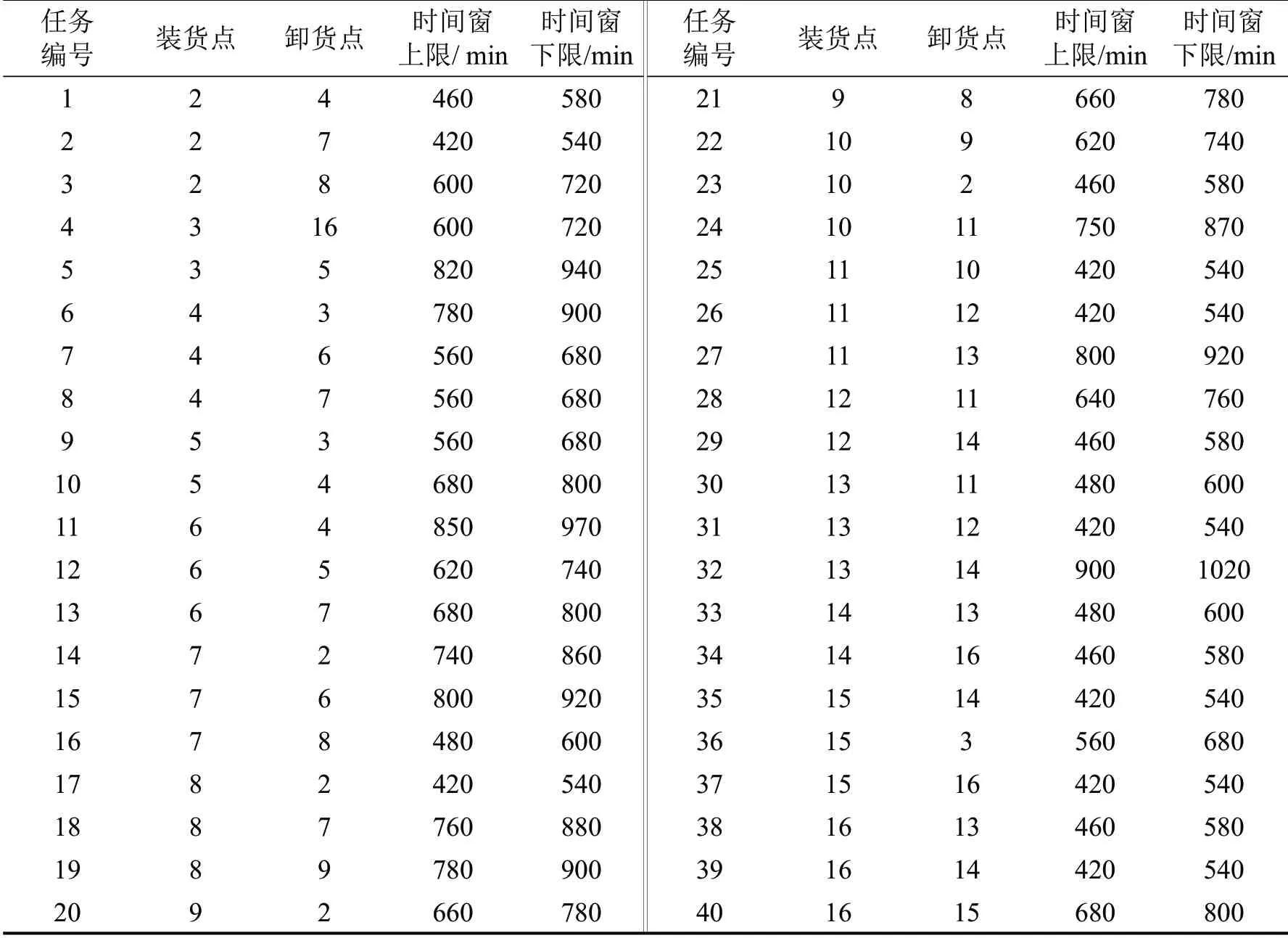
表2 运输任务信息Table 2 Transportation task information

以成本最低为目标得到初始配送方案如表3所示，配送车辆按该方案执行至时间为660 min时，累计接到新增运输任务信息如表4所示。将新增运输任务分别并入到3种调度方案中进行比较，派车方案如表5所示。

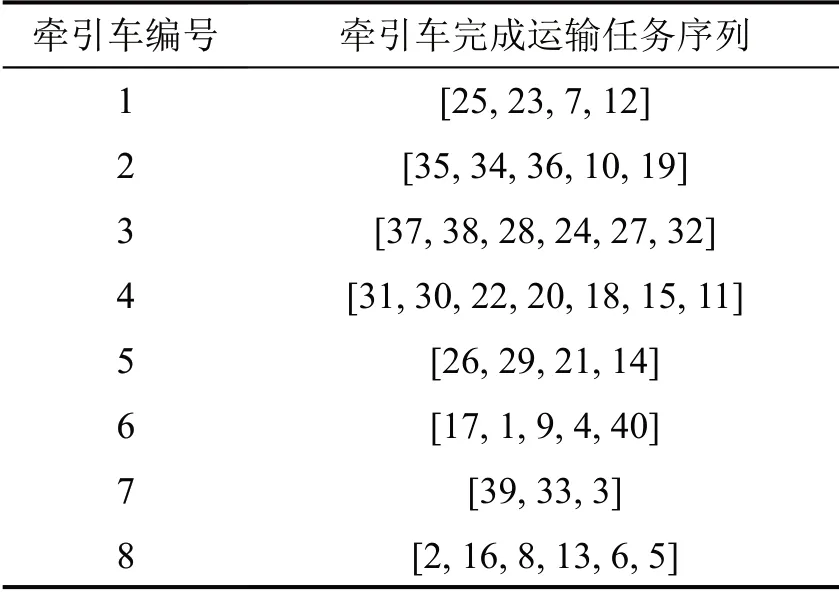
表3 原优化运输方案Table 3 Original optimized transportation plan

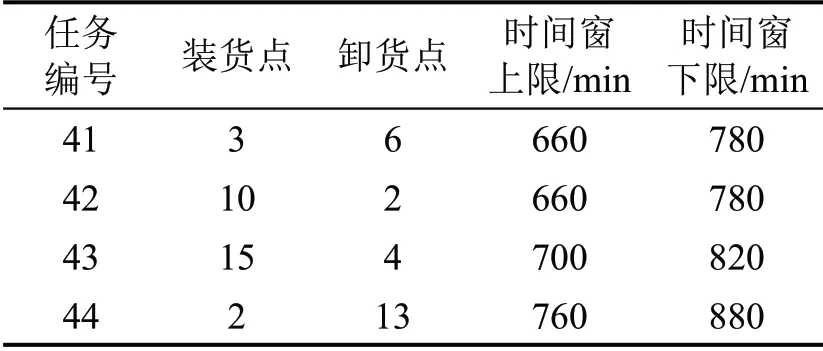
表4 新增运输任务信息Table 4 New transportation task information

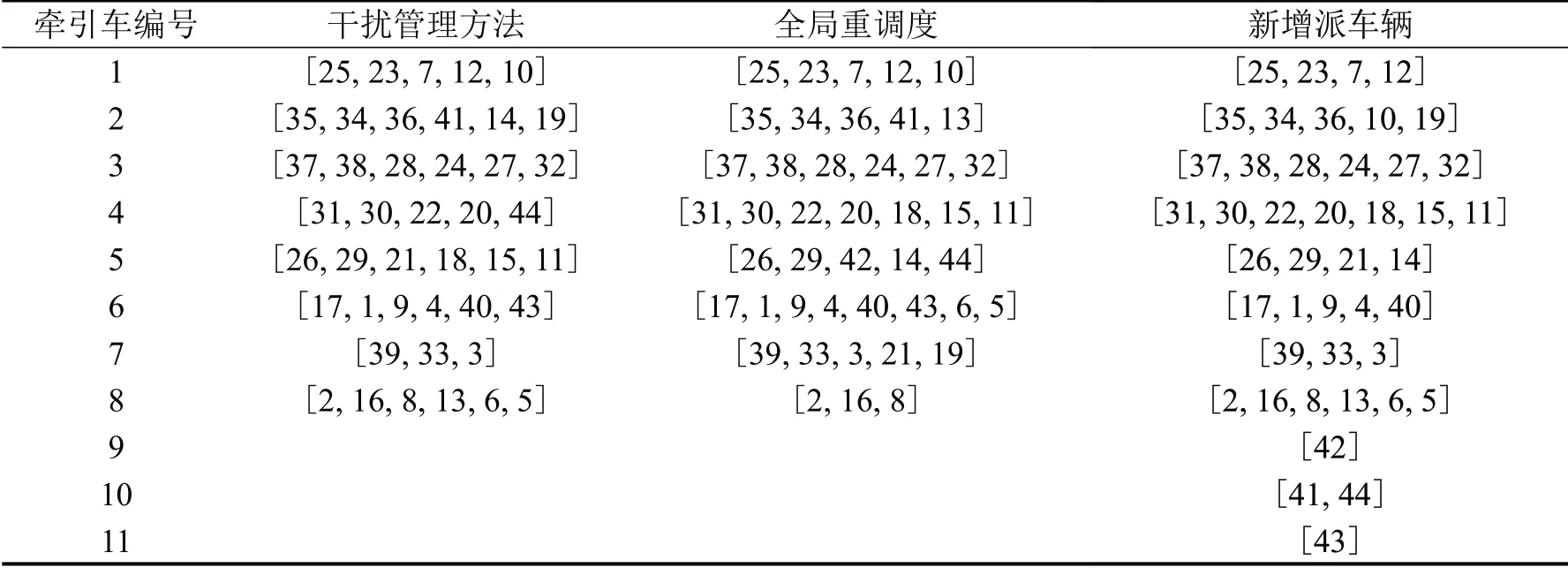
表5 3组优化方案最终牵引车运输任务序列Table 5 Final tractor transportation task sequence of three groups of optimization schemes

本文提出的干扰管理方法与其他两种处理方法对比结果如表6所示。对比结果可以看出，在路径偏离上，全局重调度方案略低于干扰管理方法，表明若系统单纯考虑成本最低，不考虑时间偏离对客户满意度是否影响的情况下，全局重调度方案具有明显优势；在时间偏离上，本文方案明显优于全局重调度法，高于新派车辆法；在广义总费用偏离上，本文干扰管理方法明显低于全局重调度和新派车辆方法。若采取新派车辆法，虽然降低时间偏离，但浪费了当前配送车辆的运力，增加了新派车辆的成本和路径偏离的成本；若采取全局重调度方案，尽管降低路径偏离成本，但时间偏离成本明显增加，可以看出全局重调度法是从牺牲客户满意度的情况下进行扰动恢复。在实际中，系统既要考虑路径变动带来的成本偏离，也要考虑配送时间变动对客户的影响，从而产生的时间偏离成本。

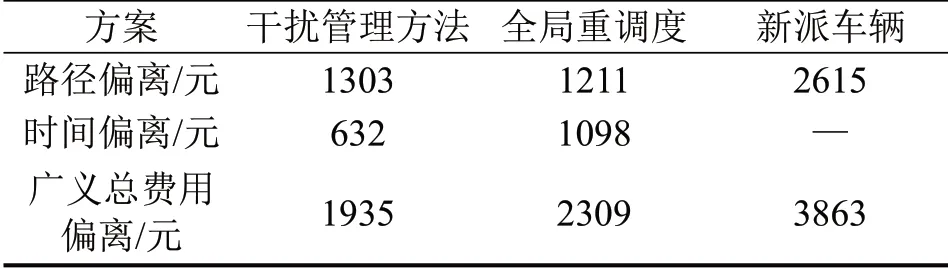
表6 3种方案结果比较Table 6 Comparison of results of three schemes

综上，在考虑路径偏离和时间偏离的影响上，本文研究的干扰管理方法有明显的优化，在保证甩挂运输组织有效运营的同时更好地保证对客户的服务质量，一定程度上减少干扰事件对系统的扰动。

6 结论

本文以甩挂运输过程中新增运输任务的出现作为研究，在满足客户时间窗最小配送成本为目标的基础上，考虑路径偏离成本、客户服务时间偏离成本构建干扰管理模型。本文干扰管理方法相较于全局重调度法和新派车辆法，能够更大程度降低成本的增加，降低由于客户服务时间偏离而产生的时间惩罚成本，进而降低广义总费用偏离，降低系统扰动程度。