基于不确定理论的常规公交车辆调度优化

薛运强，郭军，钟蒙，安静

（1.华东交通大学，交通运输与物流学院，南昌 330013；2.北京工业大学，城市建设学部，北京 100024）

0 引言

成本和效率是常规公交可持续运营的基础。公交车辆调度优化问题是在保证公交公司不亏损、服务水平合适的前提下，如何计划安排车辆发车间隔和车型配置，使得公交运行与乘客出行总成本消耗最低，并降低行车延误。公交车辆调度优化研究具有积极的理论意义和实践价值[1]。

关于常规公交车辆调度优化问题，国内外学者都做了相应研究。在车辆调度优化方面，姚恩建[1]为解决单车型运营模式下的交通拥挤和资源浪费问题，以公交公司运营成本和乘客出行成本为优化目标，提出混合车型运营模式下常规公交线路发车间隔及车型配置优化方法。王东[2]为解决固定发车间隔和单一车型造成的资源浪费和交通拥挤问题，采用GRNN(Generalized Regression Neural Network)广义回归神经网络对常规公交客流进行预测，建立发车间隔优化模型，最后基于MATLAB求解，可以有效降低公司成本。陈晓旭等[3]为优化公交运营管理，提出基于遗传算法的公交线路发车间隔优化方法，考虑公交公司和乘客成本，以郑州市60 路公交为例，有效降低18%～26%线路总成本。在不确定理论研究方面，焦登娅[4]提出了车辆调度问题的两种新的不确定规划模型，考虑了不同卸货点顾客需求量不同、车辆运载量上限，设计了一个能有效解决车辆调度不确定规划模型的遗传算法。Rongheng He 等[5]研究了不确定因素下的多层仓库布局问题，其中月需求量和水平运输距离由不确定变量描述。此外，还讨论了机会约束规划模型与机会最大规划模型之间的关系，为寻找机会最大规划模型的最优解提供了一种有效方法。

国内外对公交车辆调度的研究主要集中在成本分析上，缺乏对公交实际运行中不确定因素的研究。文献[6]考虑了公交站点乘客不确定因素，构建了公交线路配车问题的不确定双层规划模型，但是没有考虑不同车型和候车时间、运行时间的不确定性。鉴于此，本文基于不确定理论，以最大化公交效益和最小化乘客成本为目标，考虑不同车型建立综合考虑乘客候车时间和站间运行时间不确定分布的双重不确定多目标规划模型，优化公交运行调度方案。

1 不确定理论基础知识

不确定性原理(Uncertainty Principle)最早是由海森堡于1927年提出，根据该理论不可能同时知道一个粒子的位置和它的速度。中国学者刘宝碇教授深化研究不确定理论，并在2005年出版了《不确定理论教程》，为后来学者提供宝贵参考资料。现今，不确定理论已经应用到数学、运筹学、管理科学、计算机科学等领域。

不确定理论是概率论、可信性理论、信赖性理论的统称，同时还包括其余多种理论[7]。不确定规划是处理各种不确定环境下的优化问题的理论工具[7]，通常可以从期望值、机会测度、极大化事件实现的机会这3 种角度考虑处理，最后用遗传算法、模拟退火、禁忌搜索、神经元网络或混合智能算法求解。

1.1 不确定理论相关概念

将优化问题中出现的不确定变量分为如下3 类：

(1)期望值模型(EVM)

期望值模型基于在满足期望约束成立的条件下，极大化这些不确定目标函数的期望。

式中：x为决策向量；ξ为不确定变量；f(x,ξ)为目标函数，gi(x,ξ)为不确定约束函数；i为第几个约束函数；i=1,2,…,p，p为约束函数总数；E为期望值算子。

(2)机会约束规划(CCP)

该不确定规划模型允许在一定程度上不满足约束条件，但该决策使约束条件成立的机会不小于某一置信水平，一般地，极大化乐观值的机会约束规划(CCP)模型为

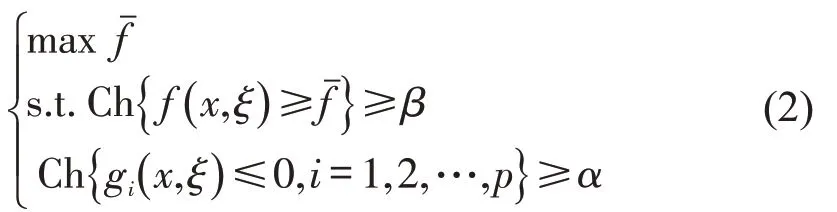
式中：α和β为给定的置信水平；ξ为不确定变量；max为目标(收益)函数的β－乐观值；Ch{·} 为可信性测度。

(3)相关机会规划(DCP)

一个复杂的决策系统通常要完成多项任务，称之为事件，决策者往往希望这些事件实现的机会尽可能的大。常见的DCP可以表示为

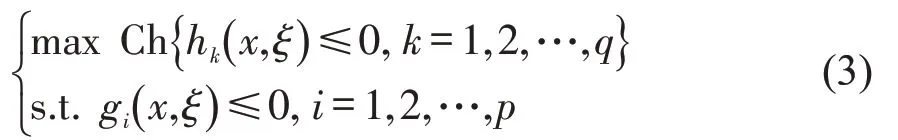
式中：hk(x,ξ)≤0 为事件，k=1,2,…,q；k为事件序号；q为事件总数。

1.2 乘客候车时间不确定分布

公交实际运行中，乘客候车时间是不确定的。它受到发车间隔、上下客流量以及交通运行路况等影响。因此，基于不确定规划，将乘客候车时间作为不确定变量之一。根据Avishai Ceder 学者的研究成果[8]，乘客平均候车时间为

式中：E(w)为乘客平均候车时间(h)；E(H)为发车间隔均值(h)；var(H)为发车间隔方差(h2)。

Avishai Ceder[8]考虑的因素忽略了道路交通情况以及其他不确定因素，在此基础上，本文将乘客候车时间不确定分布拟合成正态分布，其概论密度函数和正态不确定分布分别为

式中：ϕ(x)为正态分布的概率密度函数；μ和σ分别为均值和标准差；Φ(x)为正态不确定分布函数。

1.3 站间运行时间不确定分布

在只考虑同一车型的公交车速影响下，各公交站点之间运行时间可以简化为各站点之间距离与该公交运行速度的比值。但实际公交运行时间受多方面影响，不仅受到车速、站距、交通信号灯、交通状况的影响，还受到驾驶员、天气、车辆类型等影响。根据调查数据，各站间运行时间近似于之字形不确定分布，其之字形不确定分布为

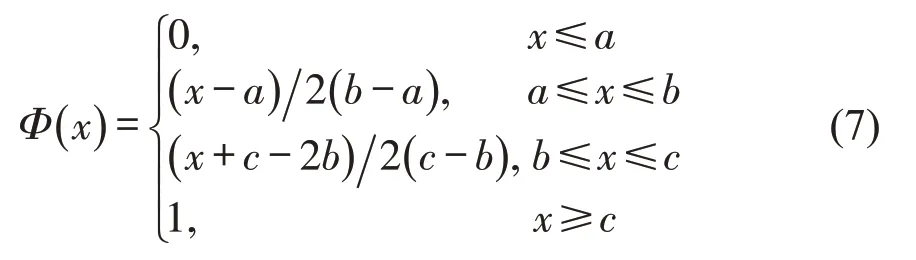
式中：a,b,c均为常数，且a ＜b ＜c，a和c分别表示变量取值的上、下界。

2 公交车辆调度优化的双重不确定多目标模型

基于乘客候车时间不确定和站间运行时间不确定双重不确定变量，考虑发车间隔和公交车型配置优化，建立以公交企业和乘客多目标优化模型，参考不确定规划模型的第一种规划模型——期望值模型(EVM)的复杂形式，建立不确定多层规划模型(MLP)。

2.1 MLP模型结构

不确定多层规划模型，为研究分层决策问题提供了模型基础。假设某最高决策者及其下属们都有他们各自的决策变量和目标函数。最高决策者可以通过他的决策变量对其下属们施加影响，而下属们则有充分的权限决定如何对他们自己的目标函数进行优化决策，这些决策又将对他们各自的上层领导和下属产生影响。多层规划着眼于各层之间的相互反馈，因此，其中通常伴随着固有的不确定性[7]。

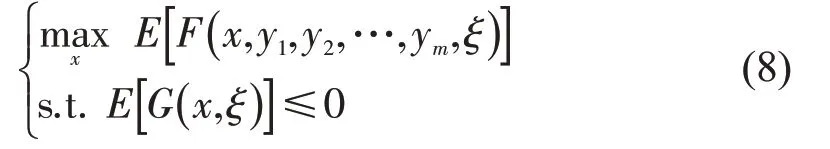
其中，对于每个yi(i=1,2,…,m)求解，即

2.2 基本假设

发车间隔和车型配置综合影响着公交公司运营成本和乘客出行总成本，是双重不确定多目标规划模型的决策变量。实际交通情况中，乘客候车时间和站间运行时间存在不确定因素，是模型的不确定变量。同时，公交公司作为决策者，能够直接改变车辆调度方案从而影响乘客进行决策，即公交公司为上层决策者，乘客为下属。为了综合考虑两方利益，追求公交公司成本最低和乘客出行总成本最低两个目标，建立双重不确定多目标规划模型，求解最科学合理的发车间隔和车型配置。

基于以下基本假设，建立双重不确定多目标规划模型。

假设1 仅考虑单向常规公交线路的运行，不考虑突发事件。

假设2 公交车经过站点后，乘客均能搭车，不进行二次等待。

假设3 乘客候车时间服从正态分布，站间运行时间服从之字形分布。

假设4 仅考虑单一公交线路运行成本，不考虑其他公交线路的影响。

假设5 影响公交公司车辆运行成本的主要因素取决于行驶里程。

假设6 全程使用同一票价。

2.3 符号定义

模型符号定义如表1所示。

表1 符号定义Table 1 Symbol definition

2.4 决策变量分析

(1)发车间隔

发车间隔作为影响公司和乘客利益的决策变量之一，它的改变会造成两者之间失去原有的平衡。同时发车间隔也是影响乘客候车时间的一个重要因素。在调查的发车间隔范围内，通过不确定正态分布函数对历史数据进行拟合，结果如图1所示，可以明显看出，发车间隔对乘客候车时间的影响。

图1 不同发车间隔的乘客候车时间拟合分布图Fig.1 Fitting distribution of waiting time of passengers with different departure intervals

发车间隔为60 min 时，乘客候车时间集中在30 min；发车间隔在6 min时，乘客候车时间明显变小，集中在3 min。由上述结果可知，发车间隔越长，乘客的候车成本越大；反之，公交发车频率就越少，其运行成本越低，但这也降低了公交对乘客的吸引。因此需要进行合理设计，在满足乘客需求的条件下，寻找帕累托最优集。

(2)车型配置

不同公交车型的运行速度对站间运行时间有着重要影响，不考虑路段交通量及信号灯的影响，以南昌市211路公交车型为例，可以分为A类车、B类车、C 类车，分别对应大（f1）、中（f2）、小（f3）型公交车。通过调查数据对不同车型的站间运行时间进行拟合，其不确定分布如图2所示。

图2 不同车型站间运行时间分布图Fig.2 Distribution of running time between stations of different models

2.5 公交车辆调度优化的双重不确定多目标模型建立

(1)乘客出行总成本

乘客出行总成本可以分为乘客候车成本和乘客乘坐车辆运行成本，即

①乘客候车成本

乘客候车成本受乘客候车时间、发车间隔及上客量影响，将乘客候车时间视为正态不确定变量，乘客候车成本为

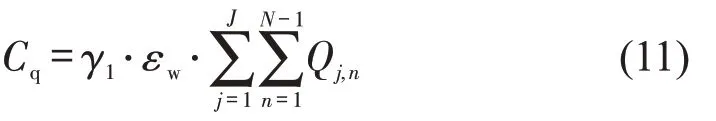
式中：j为发车车次；n为车站编号，N为车站总数。

利用乘客候车时间调查数据和式(6)进行数据拟合，得出发车间隔为xg时，乘客候车时间分布函数为

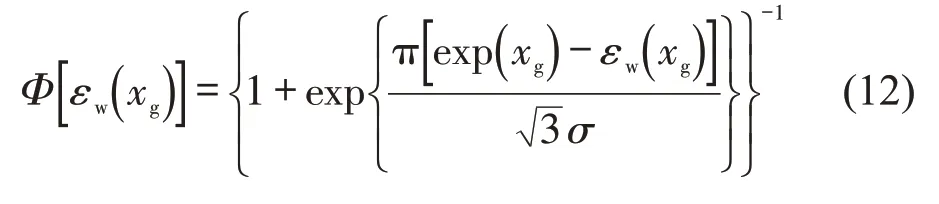
②乘客乘车成本

乘客乘车成本不仅受到站间运行时间的影响，同时车内载客率的大小也会影响乘客的心理成本，车内满载时，乘客乘车心理时间增加。考虑不同公交车型的客容量不同，其载客率的影响程度也不同。杨熙宇等[9]研究认为公交载客率感知系数δ的计算公式为

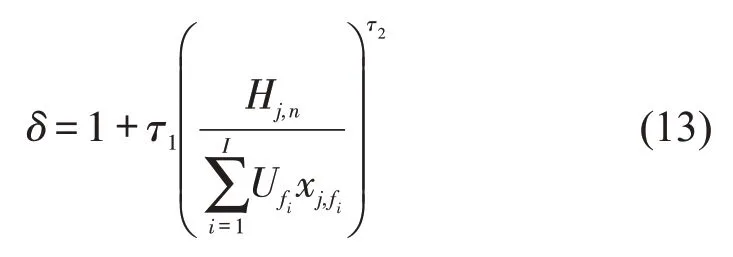
其中，τ1=0.15，τ2=2 。公交载客率感知系数，是考虑乘客感受的载客率值，为实际载客率的倍数。拥挤程度越大，感知系数也越大。

站间运行时间视为之字形分布，乘客乘车成本为

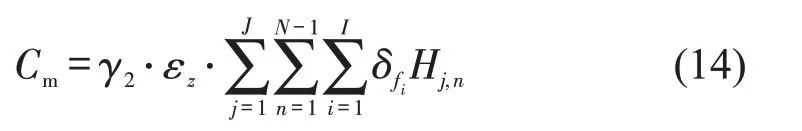
式中：I为车辆类型总数。

利用站间运行时间调查数据和式(7)进行数据拟合，得出车型为xj,fi的站间运行时间分布函数为

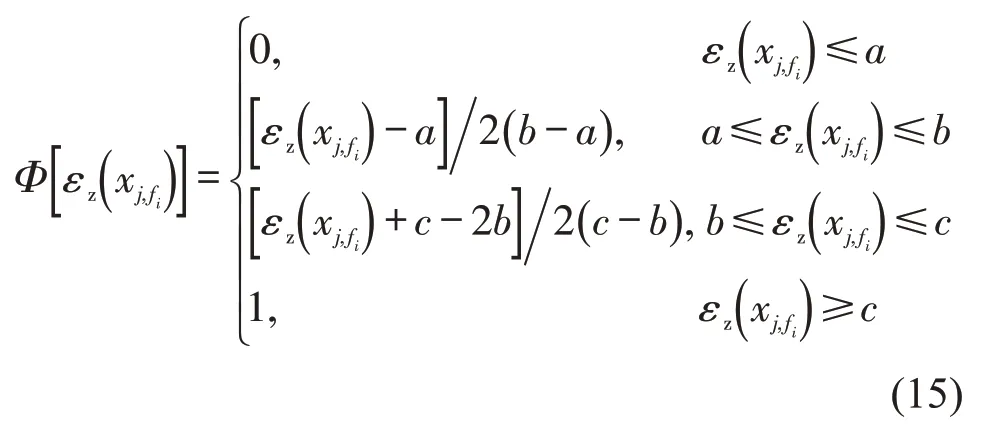
综上，乘客出行总成本为

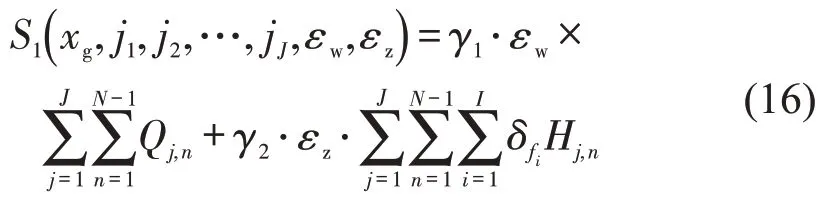
断面客流量Hjn =Hjn-1+第n站上客量-第n站下客量，可通过累加求解，且受到发车间隔影响，由式(15)可体现。发车间隔越大，单个的断面客流增大；但由于最大断面客流不能超过公交车最大容量，对应的发车次数减少，总的断面客流就减少。为了模型求解方便，本文不考虑不确定性对断面客流的影响。

(2)公交运行总成本分析

在多车型公交运行中，公交运行总成本包括公交公司员工成本和不同车型运行成本，即

①公交公司员工成本

公交公司员工成本受到站间运行时间和不同车型的影响，站间运行时间作为不确定变量，公交公司员工成本为

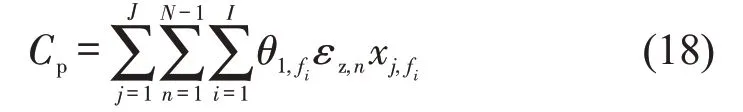
②公交车车辆运行成本

公交车车辆运行成本与运行里程和车辆类型相关，计算公式为

综上，公交运行总成本为

(3)模型目标

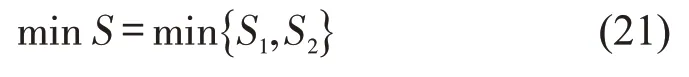
(4)约束条件

①发车间隔满足最大最小时间约束为

③最大断面载客累计客流量满足最大最小约束为

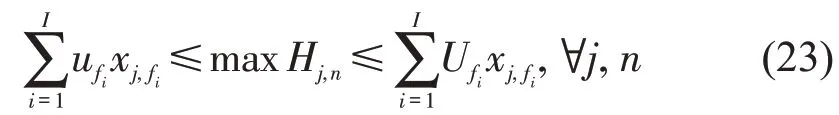
④0-1变量满足统计量为1，即

⑤载客率公式等式要求为

(5)双重不确定多目标规划模型

将其化为标准不确定多层规划模型，即

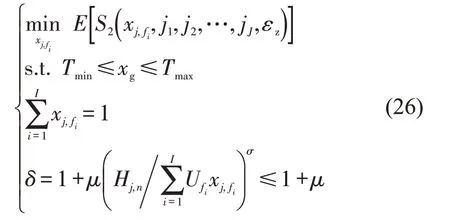
其中，对于每个ji(i=1,2,…,m)求解，即

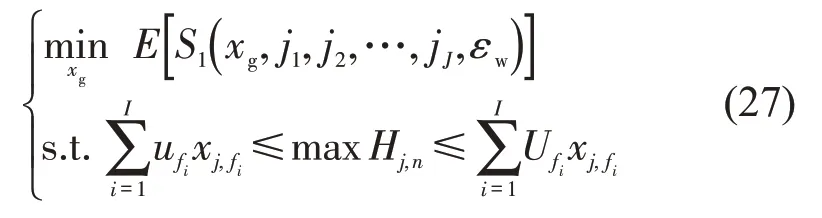
首先对式(20)取最优期望，再对式(16)取最优期望。

3 模型求解与实例分析

3.1 模型求解算法

遗传算法的基本原理就是模仿生物体基因遗传，优胜劣汰，适应性较小的个体被淘汰，最后留下适应性较强的个体，即最优解。本文求解的是非线性目标规划，适合采用遗传算法求解。在计算过程中，首先输入基本参数，在求解中调用遗传算法得出最优解。遗传算法的基本流程包括：编码、种群、适应、选择、交叉、变异、迭代、结束，具体如图3所示。在求出的解中进行择优排序，最终得出最优解。

(1)实数编码和初始化种群

调查阶段内的发车间隔为1～35 min之间，取发车间隔为整实数，采用二进制编码。

(2)适应度计算

遗传算法的适应度是用来判断群体中个体优劣程度的指标[10]，本文遗传算法求解中以目标函数的相反数maxS=max{-S1,-S2} 为适应度函数。

(3)选择、交叉、变异

染色体在遗传过程中，选择优秀个体。交叉率为0.8、变异率为0.1，精英保留率为0.2，使适应度高的染色体直接复制到下一代。在算子选择方面，采用轮盘赌选择算子、算术交叉算子、均匀变异算子。

(4)再次计算适应度

遗传不断进行，再次计算适应度，从而生成新的种群。

(5)迭代循环

设定迭代次数为200，在遗传次数达到给定值时停止运算，其中运行部分迭代如图3所示。

(6)输出适应度值最优个体

本次的发车间隔经过遗传迭代运算，求解出最优发车间隔，结合双重不确定多目标规划模型，最终确定最优的车型配置。通过枚举法求解不同车型配置的最小公交总成本，在确定最小总公交成本后，使用遗传算法求解同一车型配置下的最小乘客总成本。最后通过帕累托最优求解出最优发车间隔和车型配置。由于遗传算法取大最优，因此在目标函数前加负号，所以Z轴显示负数，如图3(b)所示。通过人工转换，将目标函数还原正值，其迭代图如图3(c)所示。

图3 遗传算法求解流程图及迭代图Fig.3 Flow chart and iterative diagram of genetic algorithm

3.2 实例分析

以南昌市211 路公交为例，运用遗传算法求解双重不确定多目标规划模型。

(1)参数设定

根据相关文献资料[6]、南昌城市发展现状及模型公式，对参数进行赋值，如表2所示。

表2 模型参数Table 2 Parameter of model

(2)车型配置及发车间隔求解

根据调查数据及历史数据，南昌公交211 路上行断面客流量及上客量如表3所示。

表3 南昌市公交211路上行各时段断面客流量及上客量Table 3 Section passenger flow and loading volume of Nanchang bus No.211 in each period

通过遗传算法，得出10种不同方案，其对应成本分布如图4所示，每一点均代表一个方案。公交运行总成本增加，乘客出行总成本降低，在这中间存在一个平衡值，使得其中一方能达到最优，一方能保证不亏损。

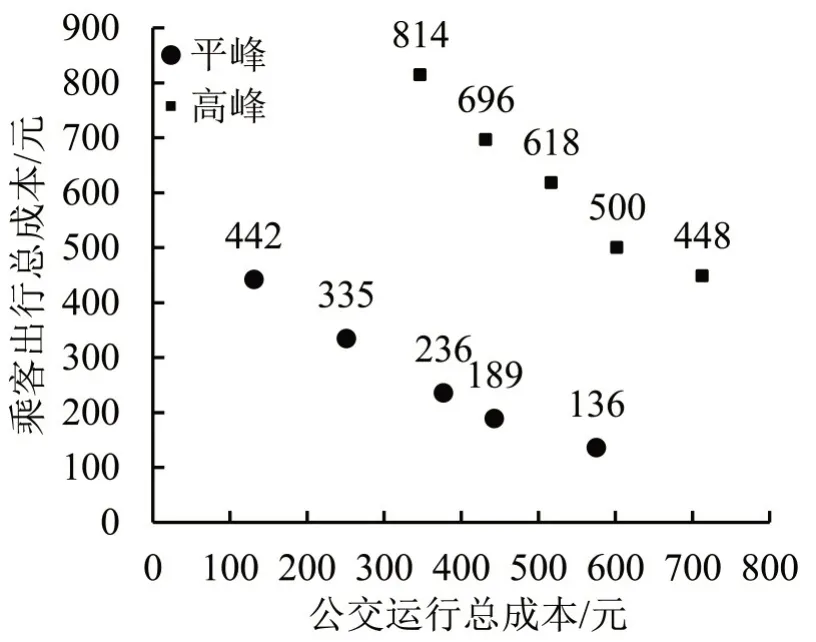
图4 不同方案的成本分析图Fig.4 Cost analysis chart of different schemes

经过方案必选及总成本计算，结合模型求解排序结果得出：公交车辆高峰时段的最优发车间隔为7.5 min，车型配置为11111112；平峰时段的最优发车间隔为8.6 min，车型配置是为3332333。

3.3 仿真分析

通过模型已求解出最优成本下的发车间隔和车型配置，如图5所示，但公交实际运行效率不清楚，极可能出现成本优化，而效率降低的情况。因此，利用SUMO 软件，进行现状及优化后的仿真分析，得出延误数据，并进行前后对比分析。在保证公交公司能够可持续运营的前提下，通过调整公交车辆的发车间隔和车辆配置，减少公交运行15 s延误，如图5(b)所示，提高了公共交通的运行效率，证明了模型优化结果的可靠性。

图5 方案优化前后对比图Fig.5 Comparison chart before and after optimization

4 结论

本文考虑候车时间和运行时间双重不确定因素，基于不确定理论建立了混合车型下的公交车辆双层不确定多目标优化模型，并以南昌市211路公交为例进行单条公交的单向线路运营优化，利用遗传算法python 编码对模型求解。通过对车辆调度方案的成本与延误数据对比来评价方案的优化效果，得出了最佳公交车辆调度方案。

与以往研究不同的是，除了考虑不同车型在公交运行中的影响，本文还综合考虑了双重不确定因素影响。分别选取平峰时期和高峰时期的线路运行数据为基础数据，对不同时段的车型配置分别安排，为公交运行提供了不同时段的车辆配置方案。仿真结果表明，考虑不确定因素的公交车辆合理调度安排有利于充分利用公交车辆资源和提高公交运行效率。

由于本文数据有限，仅考虑了单条公交线路，下一步将对多条公交线路网络运行优化进行研究。此外，公交车内拥挤程度对公交乘客出行选择的影响也需要考虑，以及不确定因素与乘客出行有限理性选择行为的关系，进一步影响公交运营调度也是有待讨论的话题。

致谢

感谢美国MORPC(Mid-Ohio Regional Planning Commission)的Liu Yan博士润色修改英文摘要。