面向单向交通路网的绿波协调设计方法

卢凯，周志洁，张勇刚，赵世杰，徐广辉

（1.华南理工大学，土木与交通学院，广州 510641；2.华南理工大学，亚热带建筑科学国家重点实验室，广州 510640；3.广东警官学院，治安系，广州 510230）

0 引言

我国从20 世纪50年代开始实施单向交通，近年来，国内许多城市积极推广单向交通的应用，例如北京、天津、南京、青岛、上海、大连、广州等[1]。实施单向交通能够减少交叉口冲突，增加车辆行驶安全性，减少交通事故；能够分流主干道交通，缓解主干道交通压力；能够提高车辆行驶速度，提高道路通行能力，提升交叉口通行效率，有效改善交通拥堵状况；还能够实现“立交平做”，减少对城市景观的破坏。在城市道路交通系统中，将一个区域内所有道路设置为单向道路并组合起来，即可构成一个单向交通路网。

目前，国内外学者对单向交通开展了相关研究，宫晓燕等[1]通过分析国内多个城市实施单向交通的经验，提出了一种面向单向交通的分析、设计与评价方法；龙东方等[2]以道路饱和度和车辆绕行系数最小为目标，利用双层规划模型进一步优化单向交通组织；PENG 等[3]利用仿真软件对实际单向交通进行模拟仿真分析，验证了单向交通对提高道路通行能力与服务水平的作用。现有单向交通路网研究主要集中在如何进行单向交通组织及评价实施效果等方面，对于单向交通路网的信号协调控制研究涉及较少。

对于交通信号协调控制方法的研究，目前在干道协调控制方面已有较为成熟的理论模型算法，常用算法可分为：图解法、数解法、模型法等，较为典型的有LITTLE等[4]以干道双向绿波带宽之和最大为优化目标，建立了最初形式的MAXBAND模型；GARTNER 等[5]针对路段交通流量、通行条件以及带宽需求，提出了可变带宽的干道双向绿波协调控制模型——MULTIBAND模型；荆彬彬等[6]以上、下行设计速度和公共周期为约束变量，提出一种基于双向最大绿波带宽的通用干道协调控制算法；卢凯等[7]针对进口单独放行方式的特点，提出了单独放行相位方式下的干道双向绿波协调控制数解算法。在区域信号协调控制研究方面，GARTNER等[8]较早地提出了可变带宽的绿波协调控制模型，通过加入路网闭环约束条件，将MULTIBAND模型的应用范围进一步扩展到城市区域协调控制；王昊等[9]提出将闭环约束转变为可松弛的不等式约束，建立了约束可松弛的交通网络绿波模型；LU 等[10]以交叉口实际绿灯中心时刻偏移最小为目标，建立了一种进口单独放行方式下的区域绿波协调控制优化模型。上述研究主要以双向交通作为研究对象，模型约束条件多、变量耦合性强、优化空间大、求解过程相对复杂，很少考虑行人专用相位的影响，尚未结合单向交通网络的特点进行相应的区域信号协调控制方法研究。

本文针对单向交通路网的绿波协调控制问题，建立一种面向单向交通路网的信号协调控制方法，以提升整个单向交通路网的车辆通行效率。

1 单行环路类型

在单向交通路网中，由于交叉口之间是通过单向路段连接，因此，当路网中不存在闭合环路时，通过设置相邻交叉口之间的相位差即可实现信号协调控制；而当路网中存在闭合环路时，则每一个环路中的路段行驶时间与交叉口信号配时参数存在制约关系，需要通过综合考虑整体运行效率进行信号优化设计。考虑到单向交通路网特点，通过将单向交通路网区域绿波协调控制分解为若干个单行环路的绿波协调控制，可以大大简化其优化过程。

对于一个典型的棋盘型单向交通路网，假定由m条东西向单行道与n条南北向单行道组成。为了分析方便，将由单向交通路网中网孔路段所组成的环路称为最小环路，按照由西(W)往东(E)、由北(N)往南(S)的方向，依次对各个最小环路顺序编号，并将由单向交通路网中最外侧道路所组成的环路称为最大环路。对于由最小环路组合形成的大环路，其交叉口相位差之间的制约关系可根据各个最小环路的制约关系推算出来，因此，可以选取所有的最小环路作为研究对象，但考虑到最小环路之间的相交道路会被重复计算，为了均衡单向交通路网中所有道路的作用影响，本文研究对象除了单向交通路网中所有最小环路之外，还包括路网最外围的最大环路。单向交通路网如图1所示。

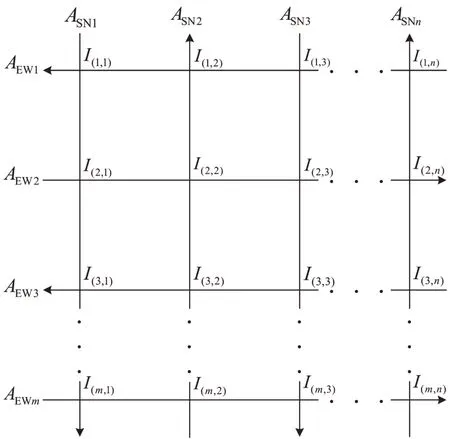
图1 单向交通路网Fig.1 One-way traffic network

在双向交通路网中，车辆通常能够从一个交叉口出发沿顺时针或逆时针方向绕环路行驶一周重新回到起始交叉口，但在单向交通路网中，由于受到单行道的限制，车辆可能无法从一个交叉口出发绕环路行驶一周重新回到起始交叉口。因此，根据车辆能否绕环路行驶一周回到起始交叉口将环路分为两类：车辆能够沿顺时针或逆时针方向绕环路行驶一周重新回到起始交叉口的环路，定义为实环路；否则，定义为虚环路。

以各个环路中的西北角交叉口I（i,j）作为起始交叉口，根据起始交叉口所在东西向单行道方向来确定环路的方向。假若单行道方向为由西向东，则环路的方向为顺时针方向；假若单行道方向为由东向西，则环路的方向为逆时针方向。因此，可以将环路分为：逆时针实环路、顺时针实环路、逆时针虚环路、顺时针虚环路4种类型，如图2所示。

图2 不同类型的单行环路Fig.2 Different types of one-way traffic loop street

2 公共信号周期优化

在单向交通路网中，为消除机动车辆与行人的交通冲突，可以考虑设置行人专用相位。由于行人专用相位的放行时间通常设定为固定值，因此，两个机动车信号相位的中心时刻点时间差主要由信号周期决定，与单行交叉口绿信比设置方案无关，本文采用绿灯中典型绿波协调设计方法优化交通信号配时。

2.1 偏移绿信比计算

(1)最小环路

以图2(a)所示的逆时针实环路为例，假设交叉口I（i,j）到I(i+1,j)的行驶时间为t(i→i+1,j)，交叉口I(i+1,j)到I（i,j）的行驶时间为t(i+1→i,j)，交叉口I（i,j）到I(i,j+1)的行驶时间为t(i,j→j+1)，交叉口I(i,j+1)到I（i,j）的行驶时间为t(i,j+1→j)。交叉口I（i,j）由南(北)进口放行相位到东(西)进口放行相位的转换时间为Δt1(i,j)，由东(西)进口放行相位到南(北)进口放行相位的转换时间为Δt2(i,j)。由于相位相序的不同会对机动车相位转换时间产生影响，因此，需要根据相位相序进行转换时间的计算分析。

①若相位相序为北(南)-东(西)-行人，则相位转换时间分别为

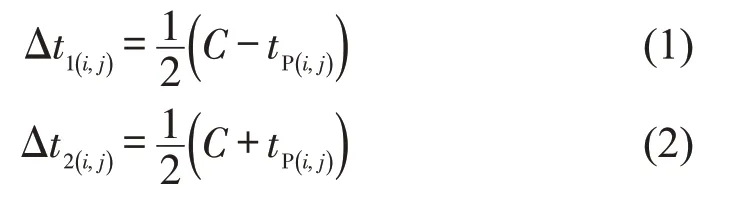
式中：C为信号周期大小；tP(i,j)为交叉口I（i,j）的行人专用相位时间。当交叉口不存在行人专用相位时，行人专用相位时间设置为0，相位转换时间均为

②若相位相序为东(西)-北(南)-行人，则相位转换时间分别为

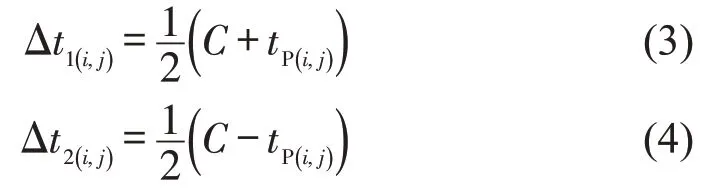
为保证每条单行道均可以获得理想的绿波协调控制效果，考虑到协调相位之间的转换时间可以得到图2(a)所对应的理想协调效果满足条件为

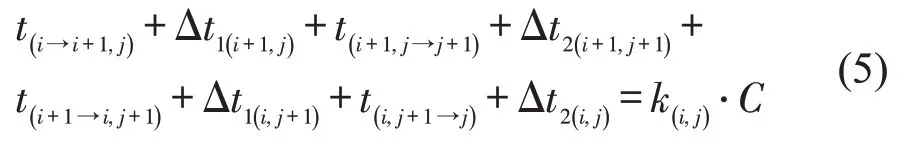
式中：k（i,j）为保证西北角交叉口为I（i,j）的环路获得理想协调效果的整数变量。

当实际交通条件不能满足式(5)，即行驶时间与相位转换时间之和并非整数倍个公共信号周期时，可以计算所有行驶时间与相位转换时间之和与若干个公共信号周期的偏移量，将偏移量与公共信号周期的比值作为环路偏移量比，表示实际情况与理想情况之间的偏差。对于图2(a)的逆时针实环路，其偏移量比Δr(i,j)的计算公式为

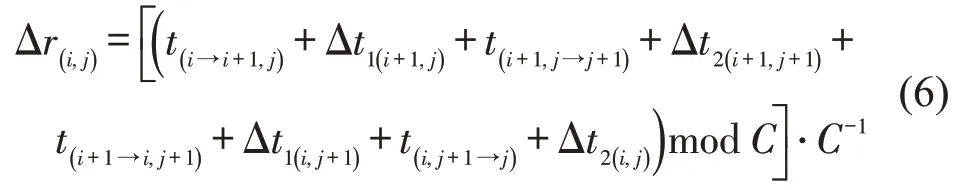
式中：mod为求模运算。

同理，可得图2(b)所示顺时针实环路的偏移量比Δr(i,j)计算公式为

对于图2(c)所示的逆时针虚环路，若路段行驶方向与环路同向，则相对应的行驶时间取正；若路段行驶方向与环路反向，则相对应的行驶时间取负。根据协调相位之间的转换时间与交叉口之间的行驶时间，可以得到理想协调效果满足条件为

可得图2(c)所示逆时针虚环路的偏移量比Δr(i,j)计算公式为

同理，可得图2(d)所示顺时针虚环路的偏移量比Δr(i,j)计算公式为

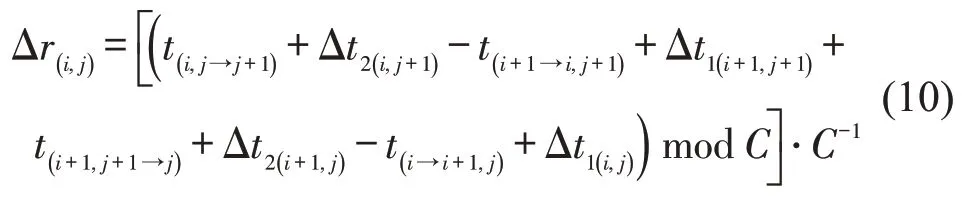
偏移绿信比是指实际交叉口绿灯中心时刻点相对于理想交叉口绿灯中心时刻线的上下偏移量与公共信号周期之比[7]，其取值范围定义在(-0.5,0.5]之间。通过变换环路偏移量比，可以得到环路偏移绿信比Δλ(i,j)为

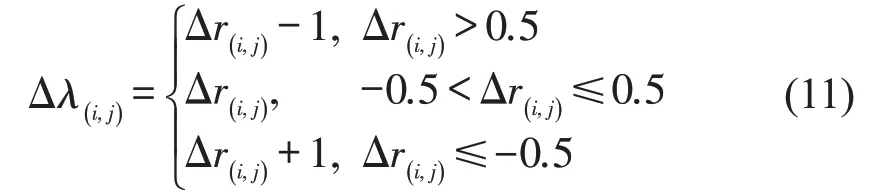
(2)最大环路

当最大环路为逆时针方向时，如图1所示，可以推出最大环路获得理想协调效果的满足条件为

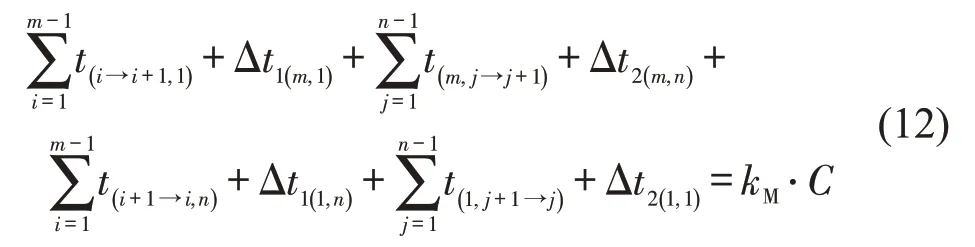
式中：kM为保证最大环路获得理想协调效果的整数变量。

若最大环路的方向与路段通行方向一致，路段的行驶时间取为通行时间；若最大环路的方向与路段通行方向不一致，路段的行驶时间取为通行时间的相反数。

当最大环路为顺时针方向时，其理想协调效果满足条件为

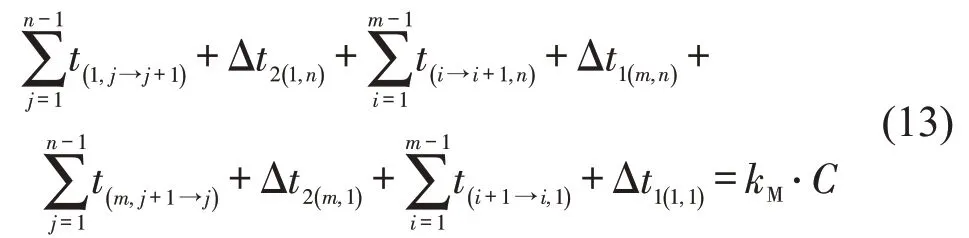
可以推出，逆时针与顺时针最大环路偏移量比ΔrM分别为

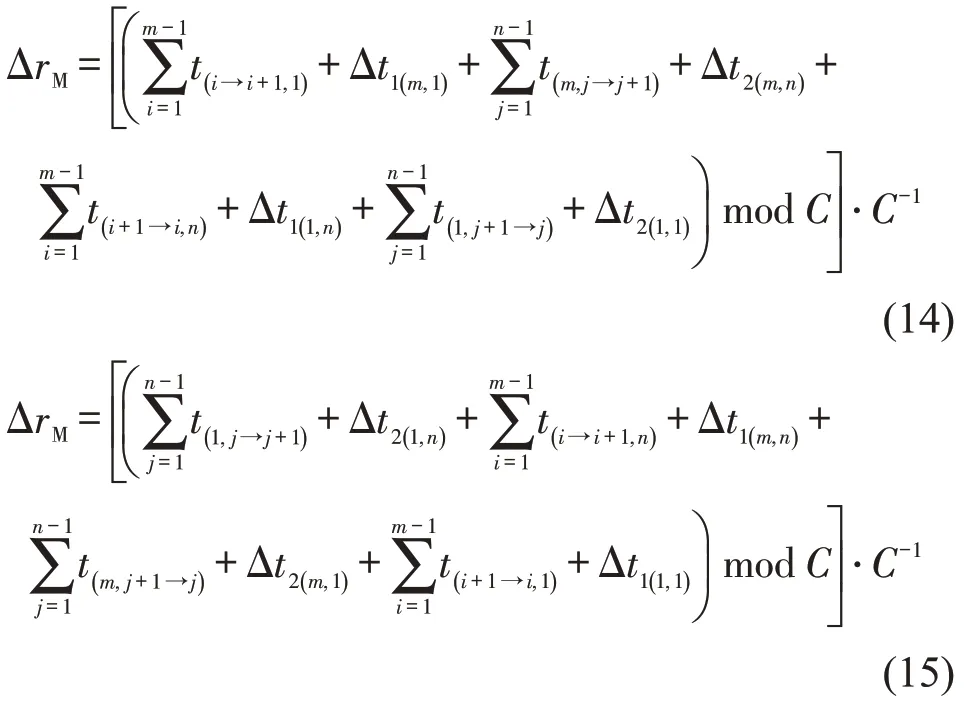
同样，通过变换最大环路偏移量比ΔrM，可以得到最大环路偏移绿信比ΔλM为

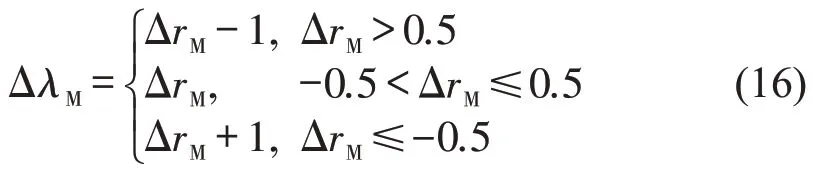
2.2 最佳公共信号周期确定

为获得尽可能宽的绿波带宽，在进行绿波协调设计时通常应使各路段的偏移绿信比尽可能小。通过环路偏移绿信比计算公式推导可以看到，调整公共信号周期取值可以改变环路偏移绿信比的大小，因此，将所有路段平均偏移绿信比最小作为优化目标，求解最佳公共信号周期。

由于最小环路之间的相交道路会被重复计算一次，因此，为均衡所有路段的作用影响，除考虑最小环路的偏移绿信比之外，还需要考虑增加最大环路的偏移绿信比。假设交叉口I（i,j）的信号周期取值范围为，则单向交通路网的公共信号周期优化范围[Cmin,Cmax] 取为对于图1所示的单向交通路网，计算所有路段平均偏移绿信比ΔλA为

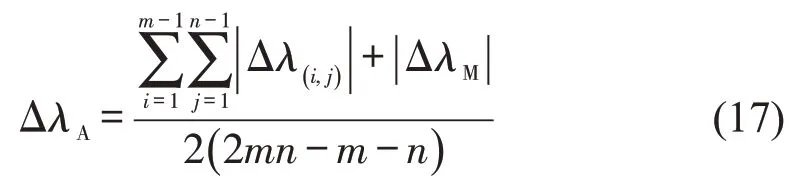
以所有路段平均偏移绿信比ΔλA最小作为优化目标，设置公共信号周期的优化目标函数PC为

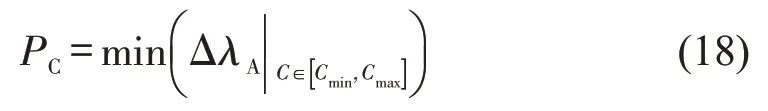
3 绿信比与相位差优化

由于绿波带宽除了受偏移绿信比大小影响外，还取决于各交叉口绿信比的分配设计方案。在此，通过引入路段偏移绿灯时间，推导交叉口相位差与绿波带宽大小的计算方法，实现对交叉口绿信比与相位差的优化。

3.1 相位差计算

假定交叉口I(i+1,j)在I(i,j)到I(i+1,j)方向上的偏移绿灯时间为Δt(i→i+1,j)，交叉口I(i,j)在I(i+1,j)到I(i,j)方向上的偏移绿灯时间为Δt(i+1→i,j)，交叉口I(i,j+1)在I(i,j)到I(i,j+1)方向上的偏移绿灯时间为Δt(i,j→j+1)，交叉口I(i,j)在I(i,j+1)到I(i,j)方向上的偏移绿灯时间为Δt(i,j+1→j)。当交叉口绿灯时间中心点向上偏移，对应偏移绿灯时间取为正数；当交叉口绿灯时间中心点向下偏移，对应偏移绿灯时间取为负数，可以推出

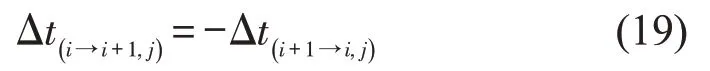
相对相位差如图3所示。同理可得

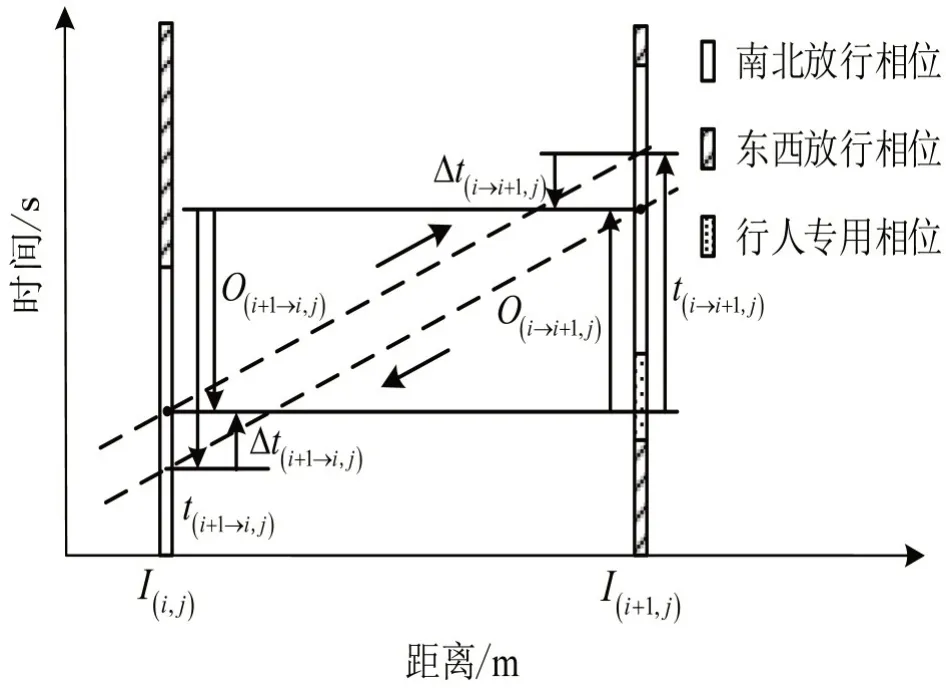
图3 相对相位差分析Fig.3 Relative offset analysis

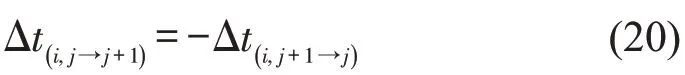
根据公共信号周期优化算法可以得到各个最小环路的偏移绿信比，将各个环路的偏移绿信比分别分配到各条单向路段上，计算各交叉口的相位差及各单行道的绿波带宽。根据环路中行驶时间与信号配时参数之间的约束关系，推出逆时针方向最小环路中各路段偏移绿灯时间与环路偏移绿信比应满足

同理，可以推出顺时针方向最小环路中各路段偏移绿灯时间与环路偏移绿信比应满足

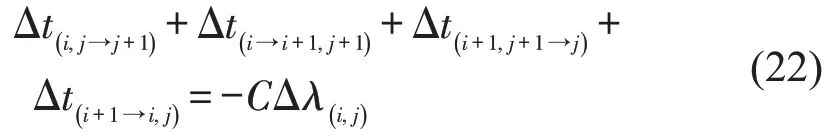
假设交叉口I(i+1,j)相对于I(i,j)的相位差为O(i→i+1,j)，交叉口I(i,j)相对于I(i+1,j)的相位差为O(i+1→i,j)；交叉口I(i,j+1)相对于I(i,j)的相位差为O(i,j→j+1)，交叉口I(i,j)相对于I(i,j+1)的相位差为O(i,j+1→j)。根据各路段的行驶时间与偏移绿灯时间可以计算相邻交叉口的相对相位差为

3.2 绿波带宽计算

假设交叉口I(i,j)东西方向的绿信比为λEW(i,j)，南北方向的绿信比为λSN(i,j)。以单行道ASNj上的南北方向相邻交叉口为例，假设交叉口I(i,j)位于交叉口I(i+1,j)上游，交叉口I(i,j)的南北放行相位中心时刻为t0，则其起点时刻为，终点时刻为根据交叉口I(i,j)到交叉口I(i+1,j)的相位差O(i→i+1,j)，可以推知交叉口I(i+1,j)的南北放行相位中心时刻为t0+O(i→i+1,j)，起点时刻为，终点时刻为t0+O(i→i+1,j)+。进而可以得到交叉口I(i,j)与交叉口I(i+1,j)的绿波带宽为

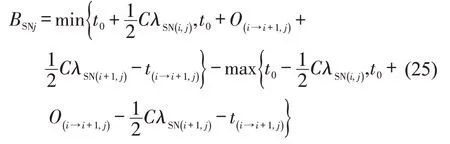
简化式(25)，可以得到单行道ASNj上交叉口I(i,j)与交叉口I(i+1,j)的绿波带宽为

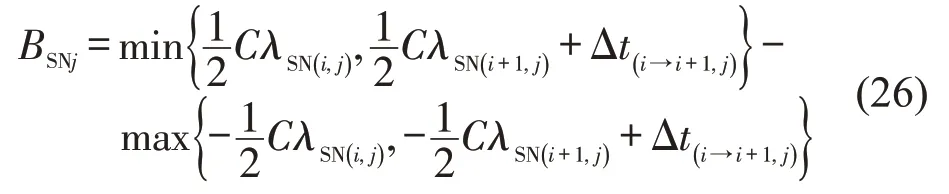
假设南北向单行道ASNj上有m个交叉口，以交叉口I(1,j)为参考点，计算南北向单行道ASNj的绿波带宽BSNj为

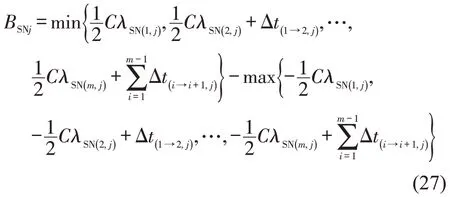
同理，计算东西向单行道AEWi上n个交叉口的绿波带宽BEWi为

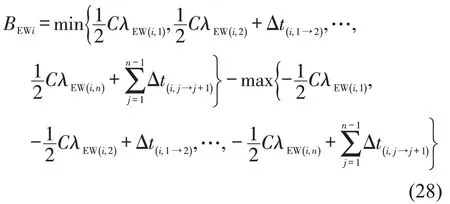
3.3 信号配时方案确定

为提高单向交通路网的整体绿波协调控制效果，应保证单向交通路网中各交叉口各相位的相位时间得到充分利用。为提高各交叉口各协调方向绿灯时间的利用效率，同时考虑到优化指标的普适性，可选取路网中所有交叉口的平均带宽占比BA，即各协调方向绿波带宽之和与公共周期的比值作为评价指标，计算公式为

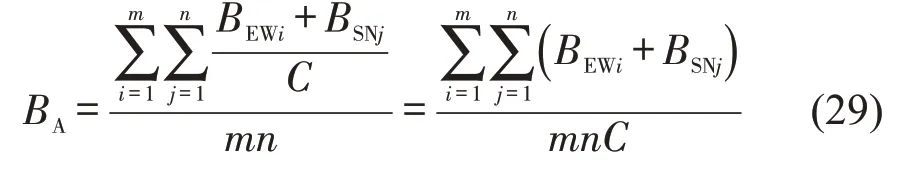
以所有交叉口的平均带宽占比BA最大为优化目标，设置绿信比的优化目标函数PG为

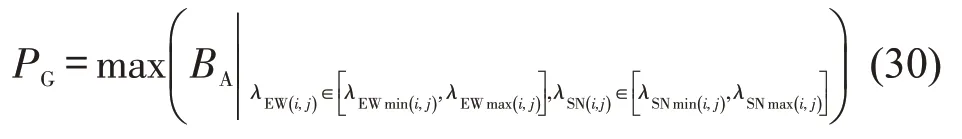
式中：λEWmin(i,j)、λEWmax(i,j)分别为交叉口I(i,j)东西方向绿信比λEW(i,j)的最小、最大允许取值；λSNmin(i,j)、λSNmax(i,j)分别为交叉口I(i,j)南北方向绿信比λSN(i,j)的最小、最大允许取值。

为获取整体最优的单向交通路网信号配时方案，首先，根据环路偏移绿信比与各路段偏移绿灯时间的关系，即式(21)和式(22)，将周期优化算法求解出的环路偏移绿信比分别分配到各路段上；然后，在各交叉口南北放行相位与东西放行相位的绿信比允许变化范围内，以交叉口平均带宽占比BA最大作为优化目标，利用绿波带宽计算式(27)和式(28)求取不同路段偏移绿灯时间分配方案和绿信比分配方案下各单行道的绿波带宽，并通过优选得到各交叉口的最佳绿信比分配方案以及各路段的偏移绿灯时间；最后，根据各路段的偏移绿灯时间，利用式(23)和式(24)求解相邻交叉口的相对相位差，得到各交叉口的最佳相位差设置方案，完成对整个单向交通路网的信号配时优化。

由于路网交叉口的绿信比优化组合空间较大，各路段的偏移绿灯时间也需要同步优化，因此，通过联立式(19)～式(29)建模与编程求解。程序的输入变量为各交叉口的绿信比与各路段的偏移绿灯时间，输出结果包括：各交叉口的绿信比与相位差、各路段的偏移绿灯时间、各干道的绿波带宽，以及交叉口平均带宽占比。

低年级是重点识字、写字的学习阶段，这时孩子们往往容易天马行空地进行表达，有些加上方言特色的语言就出来了。看图写话教学除了教会学生基本语法表达，写话包括四要素（什么时间，谁，在什么地方，干什么），还应教会学生如何观察图画，结合生活实际并根据自己的想象进行描述写话及表达感情。比如一幅一个孩子在草地上放风筝的图画，学生除了表达谁在哪里干什么，还应描述一下周围的景色，放风筝的孩子的心情。这样比较完整地表达图画的主题。学生在写话中，我们利用学生思维特点，让他们充分发挥想象写出自己想说的话才是最重要。

4 算例分析

假设某个3×3 的单向交通路网及其相邻交叉口间距如图4所示，所有道路均为两车道，绿波设计车速为36 km·h-1，车辆行驶速度在[32,40] km·h-1范围内波动。各交叉口的信号周期范围如表1所示，南北放行相位的绿信比取值范围为[0.43,0.56]，东西放行相位的绿信比取值范围为[0.30,0.43]，黄灯时间取为3 s，行人专用相位时间为10 s。

4.1 信号协调优化

(1)公共信号周期优化

按照由西往东、由北往南的方向，依次对各个最小环路进行顺序编号为①、②、③、④，如图4所示。可以确定环路①为逆时针实环路，环路②为逆时针虚环路，环路③为顺时针虚环路，环路④为顺时针实环路，最大环路为逆时针虚环路。

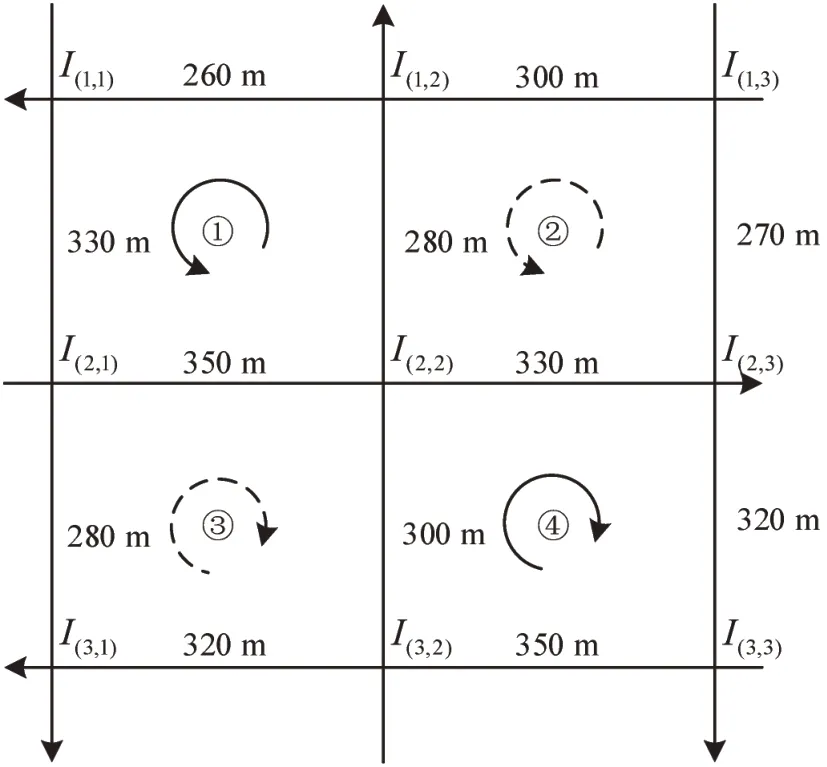
图4 单向交通路网及其相邻交叉口间距Fig.4 One-way traffic network and its adjacent intersection spacings

由表1可得，公共信号周期的优化范围为[60,80]s，假设公共信号周期的优化精度取2 s，根据各个环路偏移绿信比的计算公式，可以算出路段平均偏移绿信比ΔλA为

表1 各交叉口的信号周期范围Table 1 Signal cycle range of each intersection

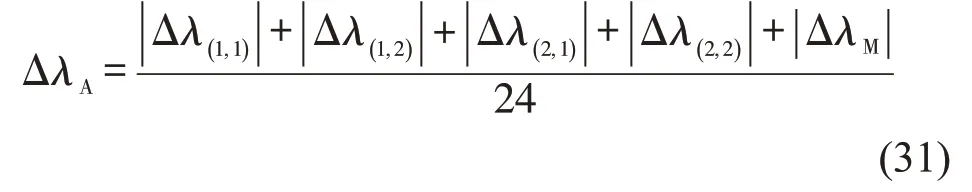
针对不同的交叉口相位相序组合，通过编程计算得到最佳公共周期为70 s，交叉口I(1,1)、I(2,2)、I(2,3)、I(3,2)的相位相序为北(南)-东(西)-行人，交叉口I(1,2)、I(1,3)、I(2,1)、I(3,1)、I(3,3)的相位相序为东(西)-北(南)-行人，各个环路偏移绿信比分别为Δλ(1,1)=0.029 、Δλ(1,2)=0.114 、Δλ(1,3)=0.129 、Δλ(1,4)=0。

(2)绿信比与相位差优化

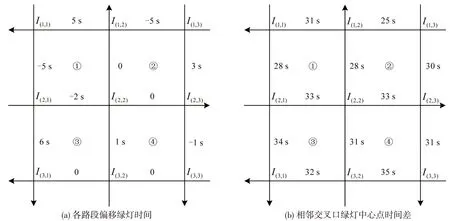
图5 各路段偏移绿灯时间与相邻交叉口绿灯中心点时间差Fig.5 Bias-time of each road section and difference of green time at adjacent intersections

表2 各交叉口的绿灯时间Table 2 Green time of each intersection

若以交叉口I(1,1)的南北相位起始点作为系统相位差设置的绝对基准点，将各交叉口南北相位起始点选作其相位差设置参考点，可以计算出各交叉口绝对相位差分别为：0，29，4，28，1，34，62，40，65 s。

根据优化计算得到的公共信号周期、交叉口绿灯时间以及相位差，做出单向交通路网的信号协调控制方案空间时距图，如图6所示。

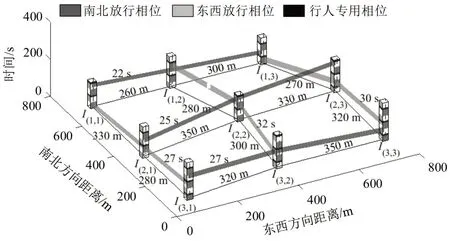
图6 协调控制方案空间时距图Fig.6 Three-dimensional time-space diagram of coordinated control scheme

可以看到，单行道AEW1、AEW2、AEW3、ASN1、ASN2、ASN3的绿波带宽分别为：22，25，27，27，32，30 s，均取得了良好的绿波协调控制效果；交叉口I(1,1)、I(1,2)、I(1,3)、I(2,1)、I(2,2)、I(2,3)、I(3,1)、I(3,2)、I(3,3)的绿波带宽占比分别为：70%、77%、74%、74%、81%、79%、77%、84%、81%，整个单向交通路网具有明显的区域控制效果。

4.2 对比实验分析

为测试本文优化方案的绿波协调控制效果，利用VISSIM 仿真软件对协调控制方案进行仿真实验。在未饱和状态下，假定各单行道进口的交通流量分别按照依次递增20%的低、中、高3 种流量输入条件进行设置，各进口道直行车辆与转弯(左转或右转)车辆的比例为5∶1，各单行道上车辆行驶速度范围为[32,40] km·h-1。仿真实验的随机种子分别取为10、20、30、40、50，实验数据统计时段为[3600,7200]s。各单行道交通流量如表3所示。

表3 各单行道交通流量Table 3 Traffic flow of each one-way road

综合选取不同随机种子的多次实验，以各单行道直行车辆的平均延误时间与平均停车次数作为评价指标，得到本文方案的仿真结果如表4所示。

表4 本文方案的仿真结果Table 4 Simulation results of the proposed method scheme

为了对比本文方法的优化效果，使用SYNCHRO软件对此单向交通路网进行优化配时，其中相位相序与本文方案相同，针对不同交通流量情况得到各交叉口的绿灯时间与绝对相位差设置如表5所示，计算SYNCHRO方案下各单行道的绿波带宽，如表6所示。由表6可知，除了单行道ASN1和ASN3外，本文方案在其他单行道上所获得的绿波带宽占比均大于SYNCHRO方案，其总体绿波效果也略优于SYNCHRO方案。

表5 SYNCHRO方案的各交叉口绿灯时间和绝对相位差Table 5 Green time and absolute offset of each intersection in SYNCHRO scheme

表6 各种方案的干道绿波带宽对比Table 6 Comparison of green wave bandwidth of each scheme

同样，以各单行道直行车辆的平均延误时间与平均停车次数作为评价指标，使用VISSIM 仿真模型对SYNCHRO方案进行多次仿真实验，得到仿真结果如表7所示。

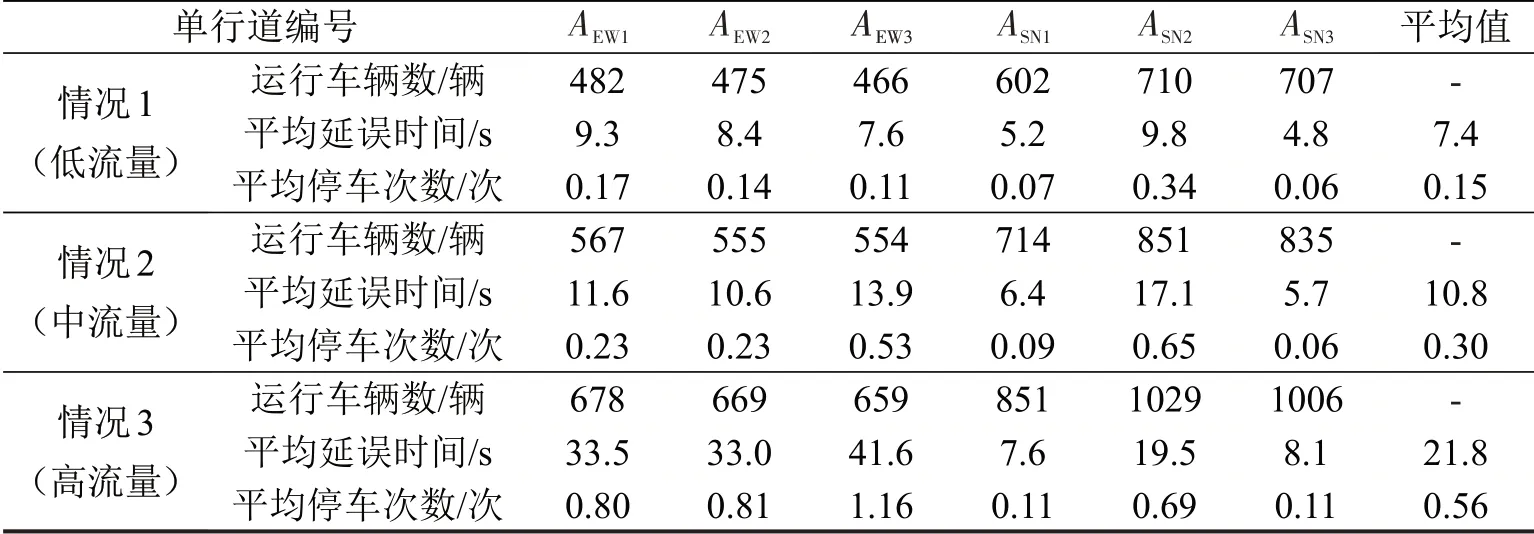
表7 SYNCHRO方案的仿真结果Table 7 Simulation results of SYNCHRO scheme

对比表4与表7可以看到，由于SYNCHRO 方案提高了单行道ASN1和ASN3的信号控制效果，导致其他单行道的协调控制效果下降。在3 种不同流量输入条件下，本文方案的路网直行车辆平均延误时间分别降低了9.0%、16.4%、26.1%，平均停车次数分别降低了31.2%、48.8%、41.6%。由此可见，本文方法较SYNCHRO 软件能够获得更好的区域绿波协调控制效果。

5 结论

本文通过引入实环路与虚环路的概念，将单行路网中所有直行绿波协调控制转化为最小环路协调控制，实现了对单行路网绿波协调控制模型的分解与重组；以所有路段平均偏移绿信比最小为优化目标，给出最佳公共信号周期优化算法，从整体设计和局部优化两个层面对多类协调控制变量进行解耦，实现了公共信号周期、相位相序与绿信比、相位差之间的分步优化；根据交叉口绿信比分配对不同协调方向绿波带宽的影响，建立路网内所有交叉口平均带宽占比最大的区域绿波协调控制模型，实现了包含绿信比在内的所有协调控制参数综合优化。案例对比分析结果表明，在不同流量输入的未饱和状态下，本文提出的方案对路网直行车辆平均延误时间与平均停车次数较SYNCHRO 方案都有较好改善，其中平均停车次数下降率均在30%以上，充分体现出本文方法在提升区域绿波协调控制效果方面的优越性。

对于同时含有单向交通与双向交通的混合型路网，如何结合单向交通与双向交通特点，建立相应的区域绿波协调控制模型算法，值得后续深入研究。