3-R(US&SPU)可折叠并联机构的运动学研究

卢帅龙, 杨富富, 陈昆精

(福州大学机械工程及自动化学院， 福建 福州 350108)

0 引言

相较于串联机构， 并联机构具有累积误差小[1]、 精度较好、 承载能力大等优点. 其中Gough-Stewart[2]平台成为6自由度并联机构的经典机构， 主要用于大负载的场合， 也是目前应用比较广泛且结构简单的一类并联机构[3]. 1985年， 瑞士Clavel博士[4]发明了3 自由度平移并联机器人， 即 Delta机械手. 因其具有高速、 灵活性强以及整体质量轻[5-6]的优点， 在快速分拣等领域发挥着重要的作用.

但工作空间小且本体占用空间大的特点在一定程度上也制约着并联机构的应用[7]. 若在并联机构中引入可折叠性能， 将会对这些性能进行改善并有利于工业应用[8]. 国内外已有一些学者在这方面做了尝试. Chung等[9-10]利用剪叉机构的可折叠性研究了一种具有2R1T运动的新型三自由度可折叠机构， 在搬运大型玻璃板以及平板电视调姿等方面得到了较好的应用. Wang 等[11]提出一种新型的可折叠六自由度并联机器人， 通过在每条支链上增加弹簧来获得更大的驱动力， 具有较大的垂直折叠能力. Xu等[12]提出一种3UU-3URU可展开单元， 并利用其构建了可展开并联机构. 房海蓉等[13]利用具有大缩放比的菱形机构作为并联机构的支链， 提出一种新型四自由度可折叠并联机构， 具有结构紧凑、 工作空间大的优点. 利用三重对称Bricard 机构的折叠性能， 成栋良[14]设计一种可折叠的 3-UPU并联机构， 极大减小了机构的空间占用， 便于运输以及搬运. 耿明超等[15]为了实时调整卫星相机的位姿提出一种6-UPRRUS折叠式六自由度并联机构， 并对其进行了动力学分析.

然而， 以上研究均通过增加一些机构单元(剪叉机构， 3UU-3URU可展开机构， 菱形机构， 三重对称Bricard 机构等)来实现可展性能， 会使整个机构的机械本体结构复杂、 稳定性较差且工作空间较小. 若利用结构自身特点来实现折叠， 不仅便于运输及存储， 还将大大简化机构的制造与装配， 也因此有助于提升系统稳定性.

本研究提出一种全新的6自由度3-R(US&SPU)可折叠并联机构， 并对其运动学进行研究. 首先利用螺旋理论对自由度进行分析. 其次， 通过建立运动学方程， 推导出其位置正逆解、 速度雅可比矩阵， 并对机构折叠性进行分析. 最后， 通过运动学仿真， 验证了理论计算的正确性. 研究结果表明， 该机构具有良好的折叠性能， 且结构简单， 可在一定程度上克服并联机构占用空间大的缺点， 具有较好的工程应用优势.

1 机构分析以及自由度计算

1.1 3-R(US&SPU)可折叠并联机构

3-R(US&SPU)可折叠并联机构如图1所示， 由动平台(H1H2H3)， 定平台(A1A2A3)， 以及3组结构相同的混合支链构成.每组混合支链都由一个闭环子链和一个转动副串联而成， 如△D1H1H3与杆A1D1串联成其中一组混合支链.该机构的定/动平台坐标系如图1所示， 取定平台△A1A2A3中心为坐标原点O，Y轴平行于A3A1，Z轴竖直向上， 并按右手定则确定X轴， 建立定平台坐标系O-XYZ(作为全局坐标系).取动平台△H1H2H3中心为原点O′，Y′轴平行于H2H3方向，Z′轴竖直向上， 并按右手定则确定X′轴， 建立动平台坐标系O′-X′Y′Z′.

3-R(US&SPU)可折叠并联机构的输入参数为θ1，θ2，θ3，l1，l2，l3， 其中：θi表示定平台上的转动副Ri的转动角度(从过Ri轴线并垂直于OXY的平面转动到Ak，Ai，Di点(i=1, 2, 3;j=2, 3, 1;k=3, 1, 2)形成的平面之间的夹角)， 并以图1(a)箭头方向为θi的正方向.li表示3个移动副所在杆DiHi的杆长.以动平台的位姿参数X1，Y1，Z1，θ4，θ5，θ6作为输出变量， 其中X1，Y1，Z1为动平台中心点O′在全局坐标系中的位置坐标，θ4，θ5，θ6为动平台的姿态参数.AiDi与转动副Ri轴线的夹角(∠AkAiDi，i=1, 2, 3，j=2, 3, 1，k=3, 1, 2)均为π-σ.因机构由3组结构相同的混合支链构成以及△A1A2A3为正三角形， 故可令|AiDi|=b， |HiHj|=d， |DiHk|=c， |AiAj|=a，i=1, 2, 3;j=2, 3, 1;k=3, 1, 2.如图1(c)所示， 取θ1=θ2=θ3=0，θ4=θ5=0，θ6=-π/3为该机构的初始位形.

图1 3-R(US&SPU)可折叠并联机构简图及模型图Fig.1 Schematic and model diagrams for the 3-R(US&SPU) foldable parallel mechanism

1.2 机构自由度计算

采用螺旋理论[16]对3-R(US&SPU)可折叠并联机构进行自由度分析. 因每组混合支链中均含有闭环子链， 故需先对其进行分析. 第I组混合支链中的闭环子链由U1S6支链和S1P1U4支链构成.因S1P1U4支链可视为无约束支链， 仅U1S6支链对整个闭环子链起到约束作用， 故以下自由度分析将去除S1P1U4支链上的运动副和构件.选取转动副R1的中心为坐标系原点o1，y1轴和转动副R1的轴线重合，z1轴竖直向上， 并按照右手定则确定x1轴， 建立第I组混合支链的分支坐标系o1-x1y1z1， 如图1(c)所示.

在初始位形下，A1，D1，H3，H1在o1-x1y1z1坐标系的坐标矢量为：

(1)

可得到第I组混合支链的运动螺旋系：

(2)

其中: 分量r1，r2，r3，r4，r5，r6分别为：

(3)

由运动螺旋系的秩为6， 得知第一组混合支链对动平台的约束螺旋系的秩为0. 因其它两组混合支链与第一组结构参数完全相同， 故三个支链对动平台的约束螺旋系的秩为0. 因此， 3-R(US&SPU)可折叠并联机构具有6个自由度， 分别是沿X轴的移动及绕X轴的转动， 沿Y轴的移动及绕Y轴的转动， 沿Z轴的移动及绕Z轴的转动.

为进一步验证3-R(US&SPU)可折叠并联机构的自由度， 根据修正的Kutzbach-Grübler公式[17]：

(4)

其中：M为机构的自由度数目； 阶数d=6；n=8为机构总的构件数量；g=9为机构运动副的数量；fi为第i个运动副的自由度数量， 共18个； 因机构冗余约束以及局部自由度的数量均为0， 故ν=0，ξ=0. 结果显示， 3-R(US&SPU)可折叠并联机构具有6个自由度， 与螺旋理论分析结果一致.

2 运动学位置正逆解

2.1 位置逆解

运动学位置逆解是已知末端操作平台的空间位姿， 反求出移动副所在杆的长度或者转动副所转动的角度. 对于3-R(US&SPU)可折叠并联机构， 就是已知动平台的空间位置和姿态， 求解3个移动副所在杆的杆长li(i=1, 2, 3)以及3个转动副的旋转角度θi(i=1, 2, 3).动平台坐标系O′-X′Y′Z′最终的姿态矩阵[18]为：

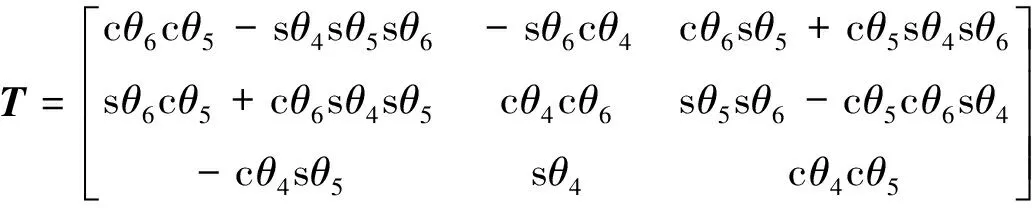
(5)

式中： cθi=cosθi， sθi=sinθi，i=4, 5, 6.

通过坐标变换方法， 可将动平台坐标系中的向量变换到全局坐标系中：

(6)

根据式(6)可得H1，H2，H3在全局坐标系中的表达， 同时根据机构的参数条件可知D1，D2，D3在全局坐标系中的坐标.因杆长|D1H3|=|D2H1|=|D3H2|=c， 故可得3个约束方程：

(7)

式中： cθi=cosθi， sθi=sinθi， cσ=cosσ， sσ=sinσ，i=1, 2, 3； 变量s1，s2，s3，s4，s5，s6分别为：

s1=cosθ4×sinθ6,s2=cosθ4×cosθ6,s3=sinθ4,s4=cosθ5×cosθ6-sinθ4×sinθ5×sinθ6

s5=cosθ5×sinθ6+sinθ4×sinθ5×cosθ6,s6=-cosθ4×sinθ5

求解式(7)即可得到3个转动副的转动量θi的两组解， 如：

(8)

其中：

根据求解的θi， 可得Hi在全局坐标系的具体坐标值， 亦可得DiHi在全局坐标系表示为：

DiHi=OHi-ODi(i=1, 2, 3)

(9)

把Di，Hi，i=1, 2, 3的坐标带入式(9)， 可得li(i=1, 2, 3)：

2.2 位置正解

运动学位置正解是已知机构移动副所在杆的长度或者转动副所转动的角度， 求解机构动平台的空间位姿参数， 在3-R(US&SPU)可折叠并联机构中就是已知θ1，θ2，θ3，l1，l2，l3， 求解动平台中心点O′点的坐标X1，Y1，Z1以及动平台的姿态θ4，θ5，θ6角度的大小.在前一节中， 已建立机构输出变量θ4，θ5，θ6，X1，Y1，Z1和机构输入变量θ1，θ2，θ3，l1，l2，l3间的6个约束方程， 如式(7)和(10)所示.它们组成含6个未知参数的高度非线性方程, 结合Matlab的fsolve函数可进行求解. 给定机构的设计参数如表1所示. 在Matlab中建立约束方程， 给定初始搜索值， 利用fsolve函数进行迭代搜索即可得到该机构的数值位置正解.任选两组机构输入参数θ1，θ2，θ3，l1，l2，l3， 得到动平台的位姿参数X1，Y1，Z1，θ4，θ5，θ6的结果, 如表2所示.

表1 3-R(US&SPU)可折叠并联机构设计尺寸参数

表2 位置正解数据

3 速度分析

(11)

(12)

对式(8)中的第二组和式(10)共6个方程两端分别对时间求导， 可确定驱动副输入的速度和动平台输出的速度之间的映射关系， 则

(13)

其中：

(14)

(15)

4 仿真分析

采用SolidWorks的Motion模块进行运动学仿真， 并与运动学理论结果进行比对. 具体地， 设动平台的初始位姿为(0， 0， 275， 0， 0， 0.349 0)T， 以5 mm·s-1的速度沿(0.6， 0.8， 0)T方向匀速运动. 经过5 s， 动平台的位姿为(15， 20， 275， 0， 0， 0.349 0)T， 得到各驱动参数的位移曲线, 如图2所示. 同时， 利用由理论分析得到的位置逆解， 在Matlab中计算得到各驱动参数的位移曲线, 如图3所示.

图2 仿真分析得出的驱动参数位移随着时间的变化Fig.2 Curves of driving displacements vs time by the simulation analysis

图3 理论计算得出的驱动参数位移随着时间的变化Fig.3 Curves of driving displacement vs time by the theoretical study

通过比对发现， 仿真分析得出的杆长位移随着时间的变化曲线与理论分析得出的曲线相差0.004%以内， 仿真分析得出的角位移随着时间的变化曲线与理论分析得出的曲线相差0.01%以内. 验证了位置逆解的正确性， 为之后的工作空间求解、 奇异性分析、 样机制作奠定了理论基础. 同时， 通过对位移曲线的观察可知， 曲线连续且平缓， 也说明了机构具有良好的运动性能.

5 机构折叠性分析

3-R(US&SPU)并联机构具有较好的折叠性能如图4所示. 当3个移动副位移最大时， 同时3个转动副的旋转量为0时， 机构高度达到最大而处于最大工作状态， 如图4(a)所示. 当机构的3个移动副位移均为0， 即l1,l2,l3都处于最短， 且3个转动副的旋转量为-90°时， 机构高度达到最小从而处于折叠状态， 如图4(b)所示. 取表1所示的机构设计尺寸参数， 机构的最大工作高度可达352 mm， 机构处于折叠状态时， 整个机构的高度为81 mm， 高度折展比约为4.35.

图4 机构展开以及折叠时的状态Fig.4 State at which the mechanism unfolds and folds

机构从完全展开变为折叠状态，li值从最大的225 mm减小至155 mm，θi值从0°减小至-90°，Z值从最大的352.4 mm减小到81.14 mm, 整个变换过程连续运动， 如图5所示， 故为工程应用提供了良好的运动性能.

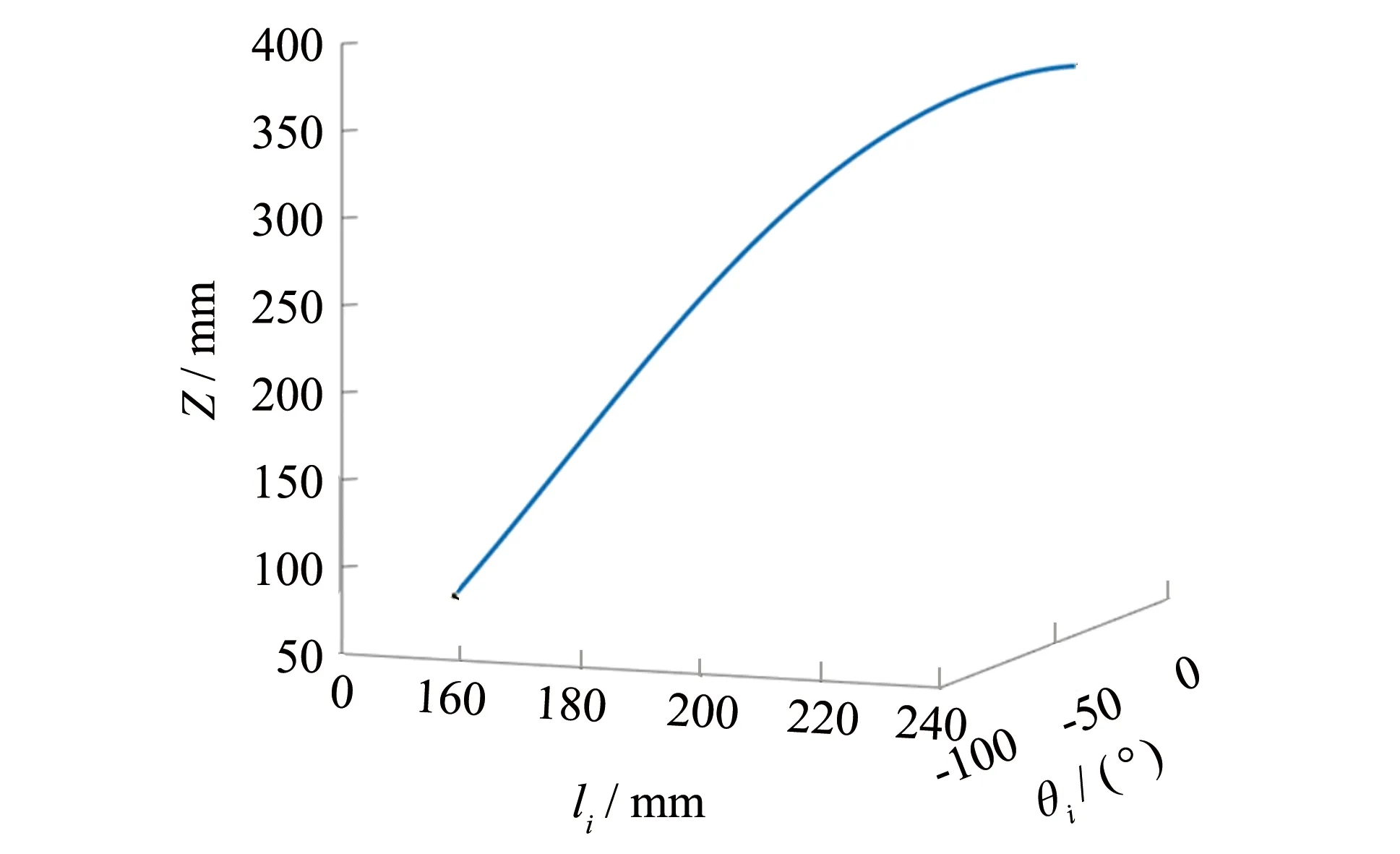
图5机构从完全展开变为折叠状态时θi值和li值的变化Fig.5 Change of θi and li values when the mechanism changes from full expansion to folded state

6 结语

结合可展结构和并联机构的优势， 提出一种新型的可折叠并联机构——3-R(US&SPU). 通过螺旋理论对其进行了自由度分析， 结果表明机构具有6个自由度. 进而分析了该机构的位置正逆解， 并得出机构的速度雅可比矩阵. 利用SolidWorks的Motion模块进行运动仿真分析， 其分析结果与理论结果相差0.01%以内， 验证了位置逆解的正确性， 为之后的性能研究奠定了基础. 当机构处于工作状态时， 可利用驱动副的连续运动， 让机构快速达到需要的工作高度. 4.35倍的高度折展比可大幅度降低运输以及维护成本， 并使机构适用于不同工作高度， 且可提高空间利用率. 同时， 该机构具有良好的运动性能， 有较好的工程应用潜力.