观测器补偿的永磁同步电机电流环多变量滑模控制

卓书芳， 黄宴委， 郭崇光

(1. 福建信息职业技术学院自动化工程学院, 福建 福州 350003; 2. 福州大学电气工程与自动化学院, 福建 福州 350108)

0 引言

电流环是永磁同步电机(permanent magnet synchronous motor, PMSM)伺服系统的内环， 其性能的好坏直接影响着整个控制系统的性能[1-3]. 由于电流环具有很强的耦合性、 系统参数摄动、 未知扰动等不确定性因素， 有必要对PMSM系统的控制策略进行深入研究[4-5]. 目前， 国内外很多学者对此作了深入的研究， 提出了诸多先进控制策略， 比如自适应控制策略[6-7]、 观测器补偿策略[8]、 滑模控制[9]等. 文献[10]针对PMSM的电流环在PID控制器的基础上， 考虑系统参数摄动， 提出一种扩展观测器实现速度补偿控制. 文献[11]在基于d-q轴电流解耦控制的基础上， 针对PMSM的位置控制， 设计一种简单观测器来补偿位置. 文献[12]提出一种扩张状态观测器估计系统参数， 采用前馈方式实现补偿控制， 提高了调速系统的鲁棒性， 但没有考虑d-q轴的解耦. 文献[13]在PI控制的基础上， 提出一种积分型电流观测器实现电流补偿控制， 提高了系统鲁棒性. 文献[14]以误差量为输入量， 实现电流环补偿控制. 文献[15]提出一种干扰观测器的PMSM位置补偿控制. 文献[16]针对PMSM的系统参数摄动等不确定性， 提出一种互补滑模控制策略来抑制系统扰动. 这些研究成果从不同方面对电机系统性能进行了提升， 其中实现电流环的解耦控制是实现电机高性能调节的关键技术之一[17-18].

针对PMSM的电流环耦合特性， 在滑模控制(sliding mode control, SMC)的基础上， 本文提出一种多变量滑模控制(multi-variable SMC, MVSMC)策略, 实现PMSM的电流环解耦调节. 针对系统参数摄动， 提出一种降阶观测器实现电流环的补偿调节. 在搭建好的PMSM实验平台上， 完成控制系统实验. 结果证明, 该方法能够很好地实现电流环解耦控制， 同时可以进一步提高电流环的调节精度.

1 PMSM的数学模型

忽略磁场饱和效应、 谐波反电动势、 磁滞及涡流损耗的影响， 磁场呈正弦分布， 则电机在d-q轴坐标系下的定子电压平衡方程[19-20]为：

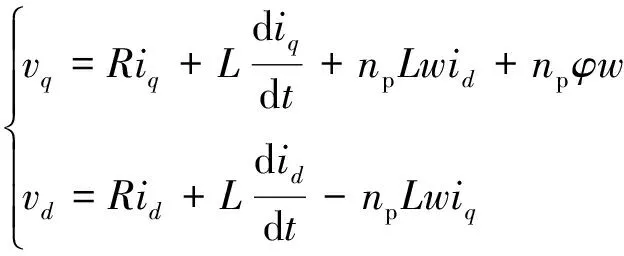
(1)

其中:vd，vq，id，iq分别为d-q轴坐标系下的定子电压值与电流；R，L，φ，w，np分别为定子电阻， 电阻电感， 电机磁链， 电机角速度， 反电动势系数， 电机的极对数.

在实际电机系统中， 参数R，L，φ相对于标称值Ro，Lo，φo有所偏差， 偏差量分别为ΔR， ΔL， Δφ， 则有，R=Ro+ΔR，L=Lo+ΔL，φ=φo+Δφ.因此， 由式(1)可得PMSM的定子电压平衡方程为：

(2)

其中：δq=ΔRiq+ΔL(diq/dt)+npΔLwid+npΔφw；δd=ΔRid+Δl(did/dt)+npΔLwid+npΔφw.

设状态变量x=[iq,id]T， 控制输入信号为u=[uq,ud]T， 则PMSM的电流环状态空间方程为：

(3)

式中：A，B为常系数矩阵；G为系统不确定量.

由式(3)可知， 电流环模型为一个双输入双输出的多变量系统， 并且具有耦合性与不确定性等特点. 对电流环设计控制器具有一定的难度. 在实际工业领域中， 通常采用单独PID策略来调节电流环， 忽略了电流环的耦合因素与不确定量的影响， 使得电机控制性能难以提高. 因此， 探索具有多变量解耦与鲁棒性强的电流环控制技术是非常有理论意义与工程实用价值的.

2 观测器补偿的MVSMC电流控制策略

2.1 MVSMC电流控制

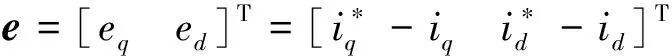
(4)

对式(4)求导， 并将式(3)带入， 可得：

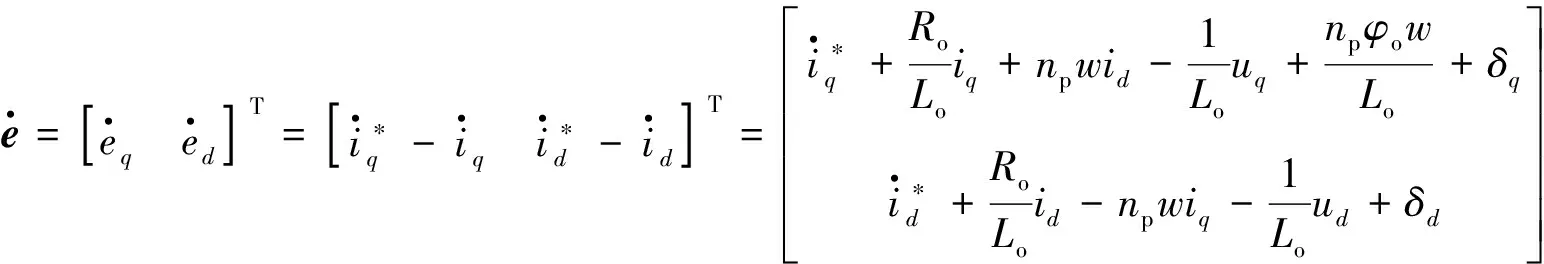
(5)

选取切换函数矢量S(x)为：

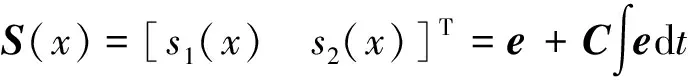
(6)

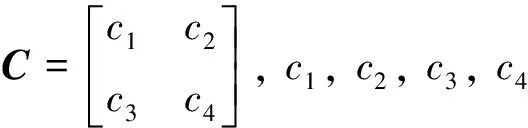
对式(6)求导， 并由式(5)， 得：

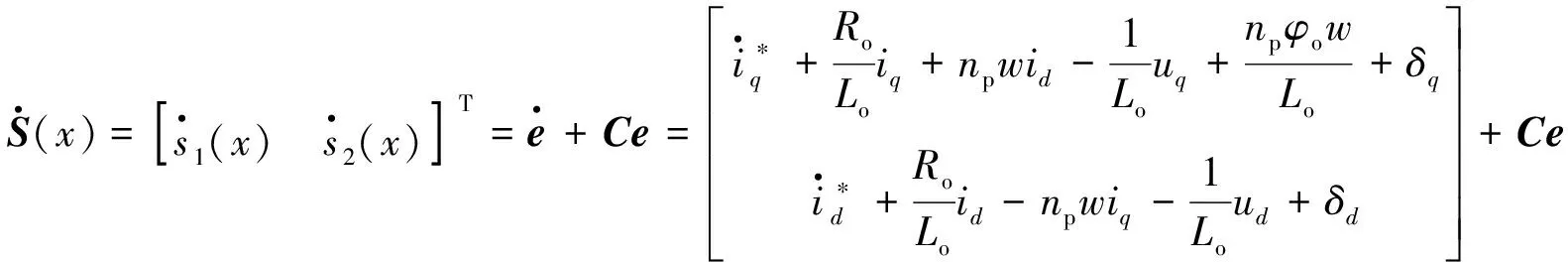
(7)

取指数趋近律

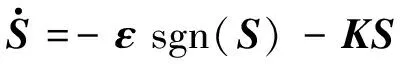
(8)

其中： 参数ε与K均为对角矩阵参数; sgn(S)为符号对角矩阵，

由式(7)和式(8)， 求得控制电压矢量为：

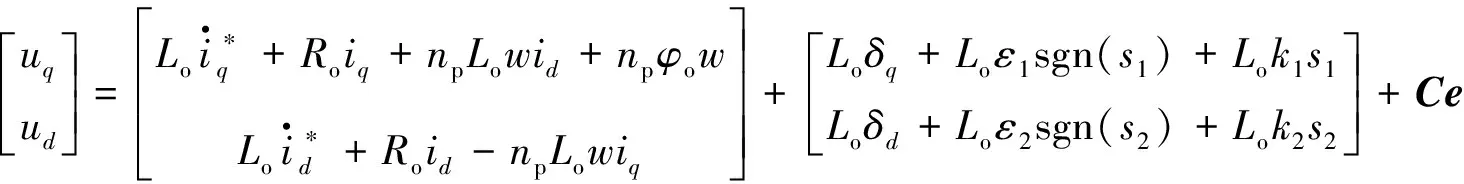
(9)

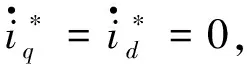
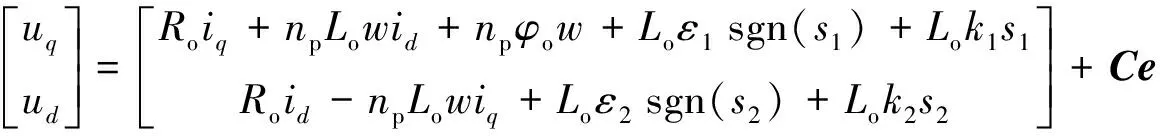
(10)

其中： 抑制系统的不确定量考参数ε1和ε2.但ε1和ε2若取值过大， 会导致高频抖振严重.因此， 在实际应用中， 都希望ε1和ε2越小越好， 就需要对电流环系统设计观测器估计不确定量， 进而实现补偿控制， 可减小ε1和ε2取值， 进而降低抖振幅值， 使系统更平稳.

2.2 观测器补偿控制

在实际伺服系统中， 由于电机参数的测量误差， 电机运行中参数的变化以及一些不确定因素的干扰， 使系统的实际模型与标定模型相差较大， 从而降低控制系统的性能. 为此， 通过设计干扰观测器来估计系统的模型误差与干扰量， 并用前馈方式补偿， 提高控制系统的性能.

观测器一般性结构如图1所示. 其中：u，d，y分别为输入、 干扰、 输出；Gp(s)为实际系统模型；Gn-1(s)为标定系统逆模型；Q(s)为滤波器.

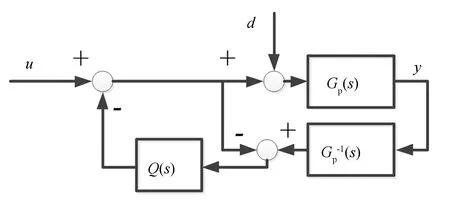
图1 观测器结构Fig.1 Structure diagram of observer

输出y与输入u传递函数为：

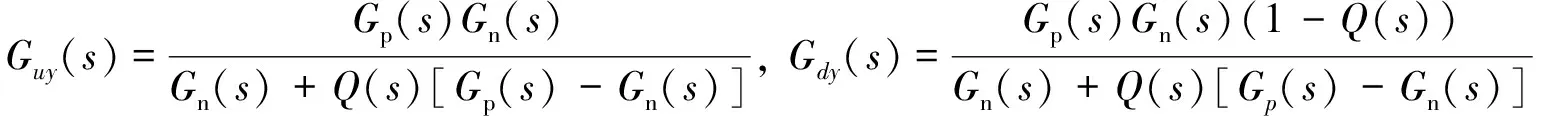
(11)

为了分析系统稳定性， 假设实际系统Gp(s)与标定系统Gn(s)存在可容许的乘性摄动Δ(s)， 则有：

Gp(s)=Gn(s)(1+Δ(s))

(12)

将式(12)带入到式(11)可得：

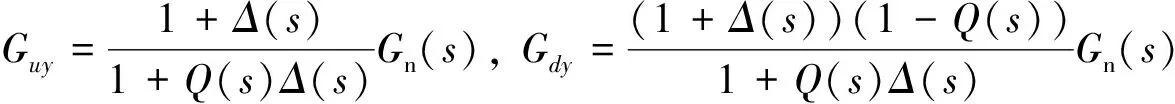
(13)

由式(13)可知， 当Q(s)=1时，Guy(s)=Gn(s)，Gdy(s)=0， 可以克服系统参数摄动和干扰的影响.

假设式(2)中不确定量δq和δd为常值量， 则有：

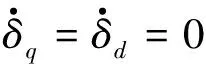
(14)

可设计降阶观测器结构如图2所示， 其中状态变量xa=[iq,id]T，xb=[δq,δd]T，A11，A12，A21，A22为系数矩阵，L为增益矩阵.

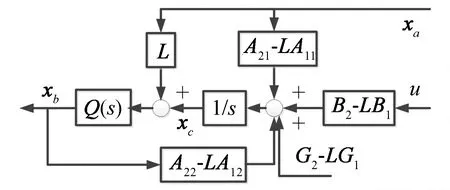
图2 降阶观测器结构Fig.2 Structure diagram of reduced order observer

构造系统降阶观测器的状态方程为：

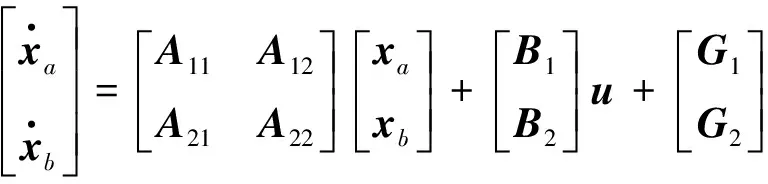
(15)

其中：

由式(15)可得到降阶观测器表达式为:

(16)

其中：L为观测的增益矩阵，L=[l1,l2；l3,l4].

(17)

(18)

对于未知λb>0， 通过选择合适的参数阵A22～LA12, 总能使观测器估计值的误差满足

(19)

则在误差收敛的扰动观测器基础上， 实际总控制电压矢量为：

(20)

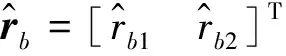
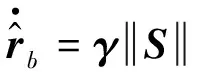
(21)

式中:γ=[γ1γ2]T，γi>0，i=1, 2.

2.3 MVSMC系统稳定性分析

选择李雅普诺夫函数为

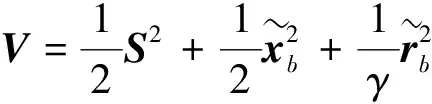
(22)

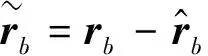
对式(22)求导得

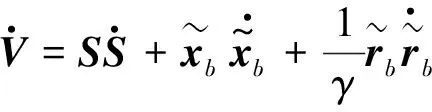
(23)

其中，

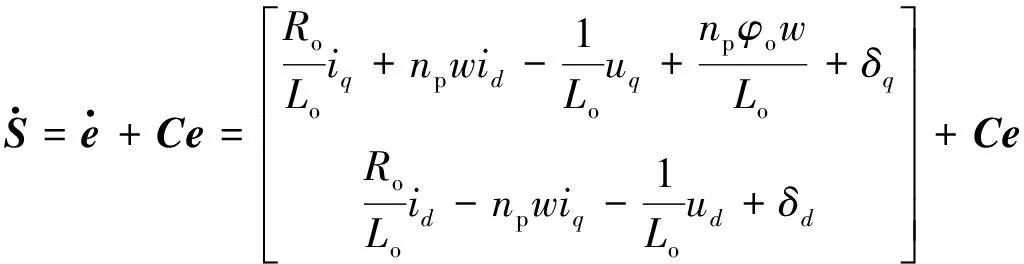
(24)

将式(20)代入式(24)， 得：

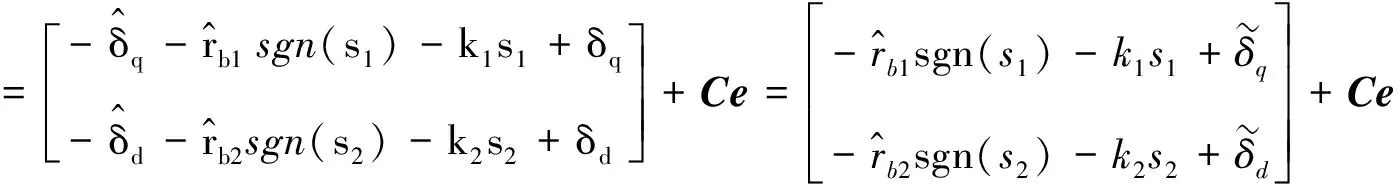
(25)

将式(25)代入式(23)， 得：

其中：k=[k1k2]T.

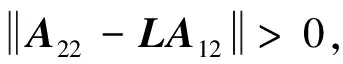
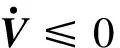
(27)

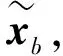
3 实验分析

3.1 实验平台设计

图3为PMSM实验平台， 由PMSM、 磁粉制动器、 DSP控制器、 逆变器、 计算机等构成. 电机型号为60CB020C， 额定电压AC220 V， 额定功率200 W， 额定电流1.27 A， 额定转速3 kr·min-1， 极对数np=4， 额定转矩0.64 N·m， 定子电阻Ro=13 Ω， 电感Lqo=Ldo=Lo=0.032 H， 磁链系数φ=0.119 Wb， 转动惯量Jm=0.000 3 kg·m2， 滑动摩擦系数Bm=0.000 1 N·m·s·rad-1； 磁粉制动器型号为CZ02， 额定转矩2 N·m， 额定电流0.5 A， 滑差功率0.15 kW. 控制器均在DSP系统中实现.

图3 PMSM平台图Fig.3 PMSM platform

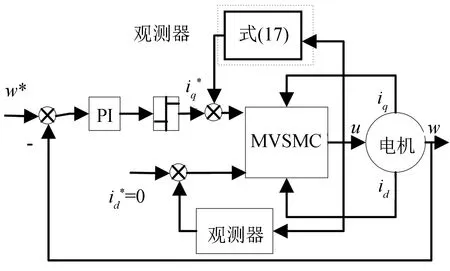
图4 PMSM控制系统结构示意图Fig.4 Diagram of PMSM control system

控制器参数： PI速度控制器参数为kp=0.016和ki=0.004. MVSMC电流控制器参数为C=[600, 0; 0, 600],ε=[0.05, 0; 0, 0.05]，K=[0.05, 0; 0, 0.05]， 观测器增益矩阵L=[-0.1, 0; 0, -0.1],Q(s)=[(20s+1)/(0.32s+1), (20s+1)/(0.32s+1)]

本方法与常规PI电流环控制策略相对比， PI控制器参数：kp=80，ki=32 000. 由C语言编程实现MVSMC策略验证实验， DSP系统的电流环采样频率为20 kHz， 速度环采样频率为0.2 kHz.

3.2 实验对比

给定角速度w*=40 π rad·s-1， 当2.0 s ≤t≤ 8.0 s时， 设定磁粉制动器的输入电流为0.12 A， 即产生负载转矩约为TL=0.4 N·m. 图5为基于观测器的MVSMC控制电流环的调速系统响应、iq、id和iA响应， 图6为MVSMC控制电流环的调速系统响应、iq、id和iA响应, 图7为PI控制电流环的调速系统响应、iq、id和iA响应. 图5～图7表明， 3种系统的速度响应时间从快到慢依次为基于观测器的MVSMC、 MVSMC和PI.

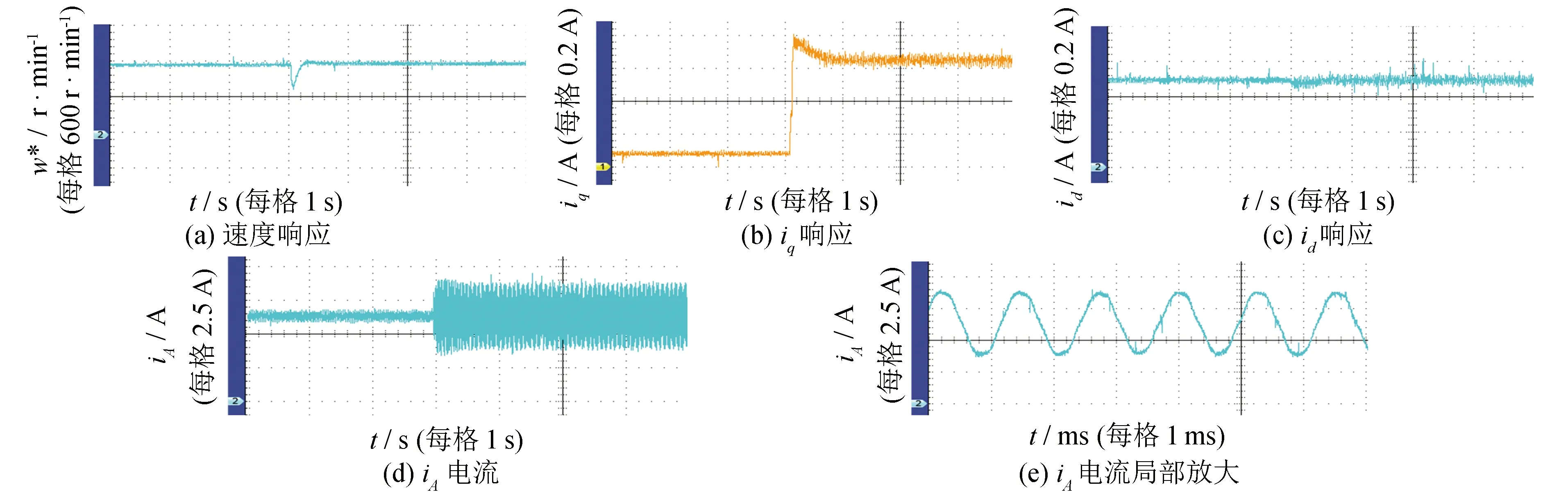
图5 基于观测器的MVSMC系统Fig.5 MVSMC system with observer

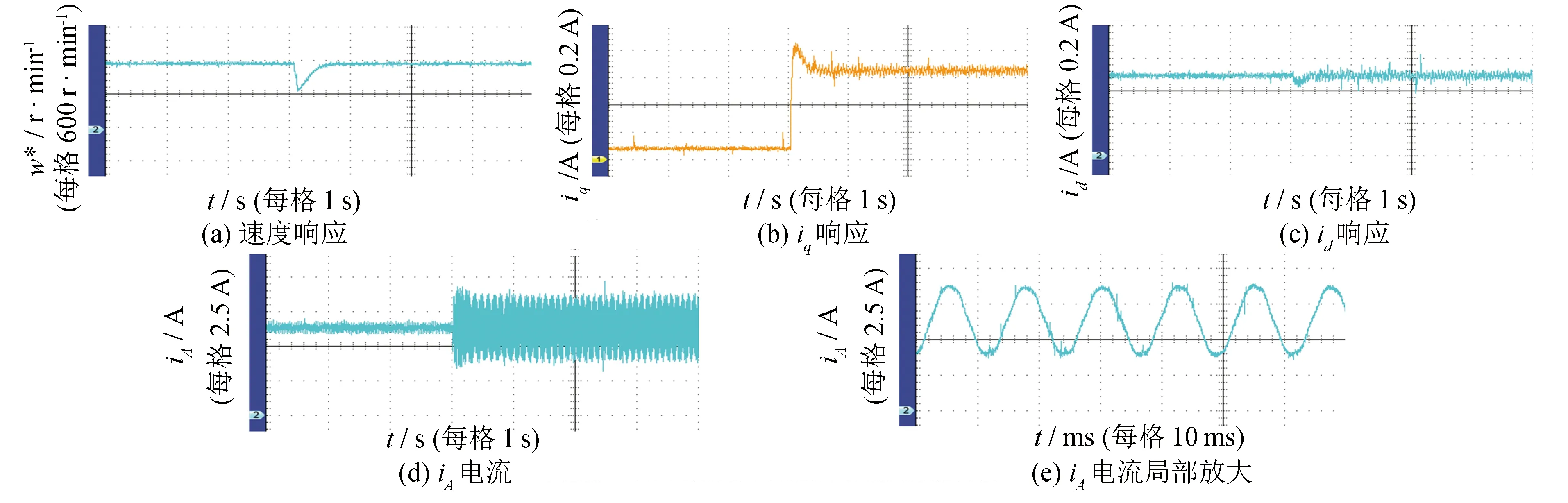
图6 MVSMC系统Fig.6 MVSMC system

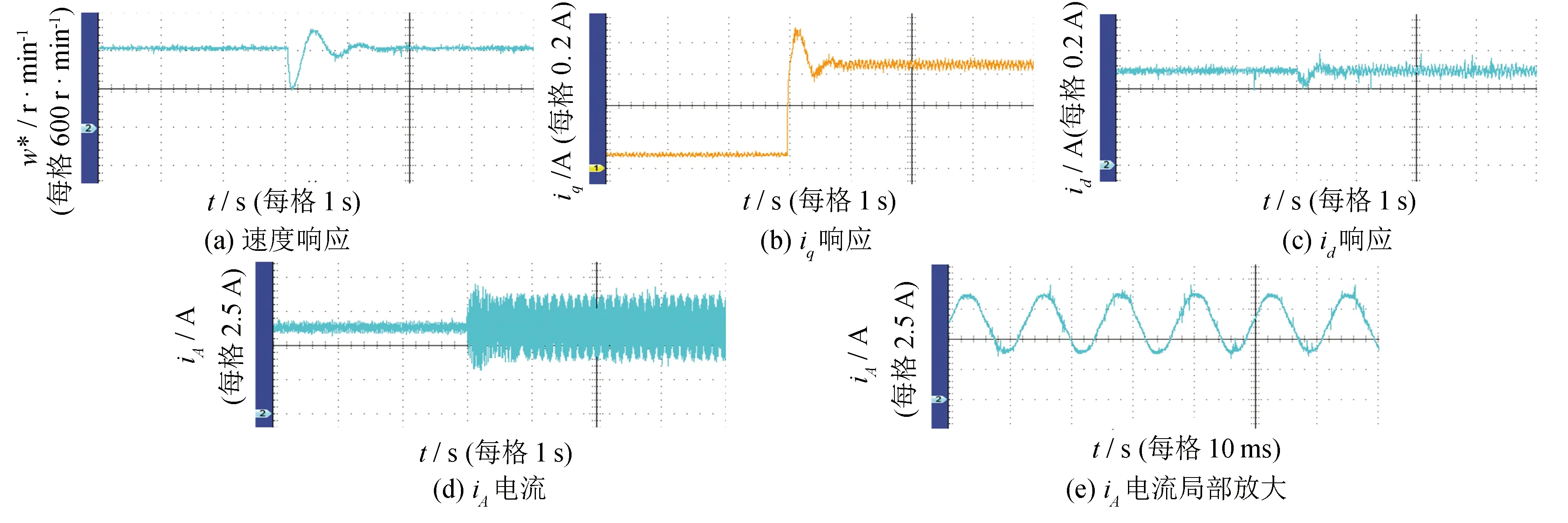
图7 PI控制系统Fig.7 PI control system

对比图5和图6可知， 在突加负载时， 图5的转速从40 π rad·s-1下降到26 π rad·s-1， 而图6则是从40 π rad·s-1下降到24 π rad·s-1， 图5中转速下降较小； 在稳态阶段，iq、id、iA的电流杂波更少； 这些现象说明, 系统有观测器时能更好地估计扰动和不确定量， 并得到更好的补偿. 对比图6和图7可知， 在突加负载时， MVSMC方法控制id， 从0.1 A减少到0.03 A， 而PI方法从0.1 A减少到0.01 A. 因此， MVSMC控制id波动更小些， 具有更好的解耦性能. 对比图5～图7的三相波形iA可知， 基于观测器的MVSMC系统的iA7波形噪声少， 正弦波形更整齐， 最差的是PI控制系统. 总之， 基于观测器的MVSMC系统能够更好地解决电流耦合问题， 并且能够很好地补偿电机系统的不确定因素和未知扰动量.

4 结语

针对PMSM电流环参数摄动、 干扰等不确定因素， 提出一种基于观测器的MVSMC方法实现电流环复合调节. 在建立含不确定量的电流环模型的基础上， 定义多变量滑模面， 推导出含不确定量的滑模控制律， 分析了不确定量是滑模控制产生抖振的源头， 进而设计观测器来补偿不确定量的影响. 从理论上分析了该系统的稳定性， 和抑制系统抖振的机理.

通过PMSM实验平台验证分析， 与常规PI电流环控制策略相比， MCSMC方法具有如下3个主要特点： 1) 更快的调速响应速度， 且速度稳态误差； 2) 具有更短的d-q轴电流响应过渡过程， 且电流稳态误差也更小； 3) 所设计的观测器能够很好地估计不确定量， 实现电流精准控制. 因此， 实验表明， 所提出的MVSMC电流环控制策略是切实可行的， 且具有更强的鲁棒性与解耦性能， 整个电机调速系统性能得到了提升.