转筒中两种形状颗粒的雪崩过程对比

王 淳，李 然，陈 泉，修文正，杨 晖

（上海理工大学光电信息与计算机工程学院，上海 200093）

引 言

颗粒物质在自然界中十分常见，如沙尘暴、雪崩和泥石流等灾害中，主要是颗粒物质的流动，颗粒物质在工业中也普遍存在[1-2]。在工业生产中，回转窑类似于滚筒，不仅用于烘干颗粒材料，还用来锻烧水泥、黏土和石灰石等颗粒物质。回转窑的转动使里面的颗粒物质充分搅拌受热，而不同形状颗粒物质的运动过程存在差异，其受热情况也会不同。回转窑类似于转筒，所以在实验中大多用转筒模拟回转窑。研究规则颗粒和不规则颗粒在转筒中的运动对工业生产的效率及安全有十分重要的意义和价值[3-4]。

在过去的研究过程中，对于转筒中规则颗粒和不规则颗粒雪崩运动的实验和数值模拟一直都在进行。2001年，Mellman[5]建立了针对不同转速条件下转筒中颗粒的运动过程变化的模型，从而确立了颗粒物质雪崩发生的条件。模型计算的结果与转筒实验的测量结果以及已发表的结果比较吻合。这一模型的建立为后续转筒中颗粒物质雪崩过程的研究提供了重要的参考价值。2011年，Liu等[6]对转筒中规则颗粒雪崩过程中颗粒的相对静止时间以及雪崩周期时间进行了研究，实验通过改变传统转速和颗粒填充率发现平均停留时间随着转速和填充度的增加而减少。他们观察到平均周转时间随转筒速度的倒数近似线性增加，但与填充度无关。2015年，Yang及其团队[7]在实验中发现转筒内不规则颗粒雪崩过程中颗粒主动层的顶部和底部的运动过程相似，但速度存在差异。实验还观察到静止时间与转筒转动速度成反比，颗粒雪崩频率随着转速的增加而增加，直到雪崩状态过渡到滚动状态。目前，对不同形状颗粒的雪崩过程的研究大多是针对其雪崩周期时间的差异以及雪崩运动速度的变化，而对于不同形状颗粒雪崩运动中运动模式的差异及其原因的研究仍然十分少见。

针对上述研究空缺，本文运用散斑能见度光谱法以及图像法[8]对转筒内两种形状颗粒的正面及侧面运动状态进行测量，选用直径为0.5 mm的球形颗粒和等效周长直径为0.5 mm的不规则颗粒在转速为0.007 5 r/s的转速下测量雪崩过程中的颗粒运动状态图像、颗粒温度[9]以及倾斜角的变化。

1 实 验

本文主要运用散斑能见度光谱法（speckle visibility spectroscopy，SVS）系统对转筒内部颗粒物质的主动层[10]上半部分中心位置的运动状态进行测量，并运用图像测量方法对转筒侧面颗粒物质的运动状态进行测量以达到准确描述的目的。

1.1 转筒系统

转筒系统主要由电机、传动装置和转筒组成。转筒由有机玻璃加工而成，形状为圆柱形，长度为200 mm，内径为146 mm。因为转筒的材质为有机玻璃，所以激光光束可以穿透筒壁照射在转筒中的球形颗粒和不规则颗粒的表面。转筒中装入一定量的颗粒物后平放在传动平台上，跟随电机进行同频转动。系统中使用的电机的转速范围为0～0.045 r/s，实验中采用的电机转速为0.007 5 r/s。SVS测量点如图1中标注所示，激光扩束后照射在颗粒上形成的散射光斑经过滤波片由线阵CCD相机拍摄采集图像。

图1 SVS实验装置图Fig.1 SVS experimental setup

1.2 颗粒材料

由于以往的研究以及模型的建立都选用球形颗粒，所以本实验选用了球形颗粒和不规则颗粒进行对比。颗粒材质选用玻璃主要是因为玻璃具有良好的透光性，激光照射在玻璃上可以形成较好的散斑图像，得到的信号可以更好地描述颗粒运动状态。通过测量球形颗粒的直径对颗粒的大小进行表征，同时通过图像解析法对不规则颗粒的大小进行表征，通过测量颗粒的费雷德直径（DF）和等效周长直径（DEQPC）得到不规则颗粒的粒径大小。不仅如此，为了准确描述不规则颗粒的具体形状，实验引入了纵横比（AR）、球形圆度（SP）与凸性（Cx）这些参数[11-12]，进一步确定不规则颗粒的具体大小。本实验通过图像法从颗粒中分选[13]出直径为0.5 mm的球形颗粒和等效粒径为0.5 mm的不规则颗粒，其显微镜下图像如图2所示。实验统计了350颗颗粒的形状参数，其特征参数如表1所示。

表1 颗粒特征参数Tab.1 Particle characteristic parameters

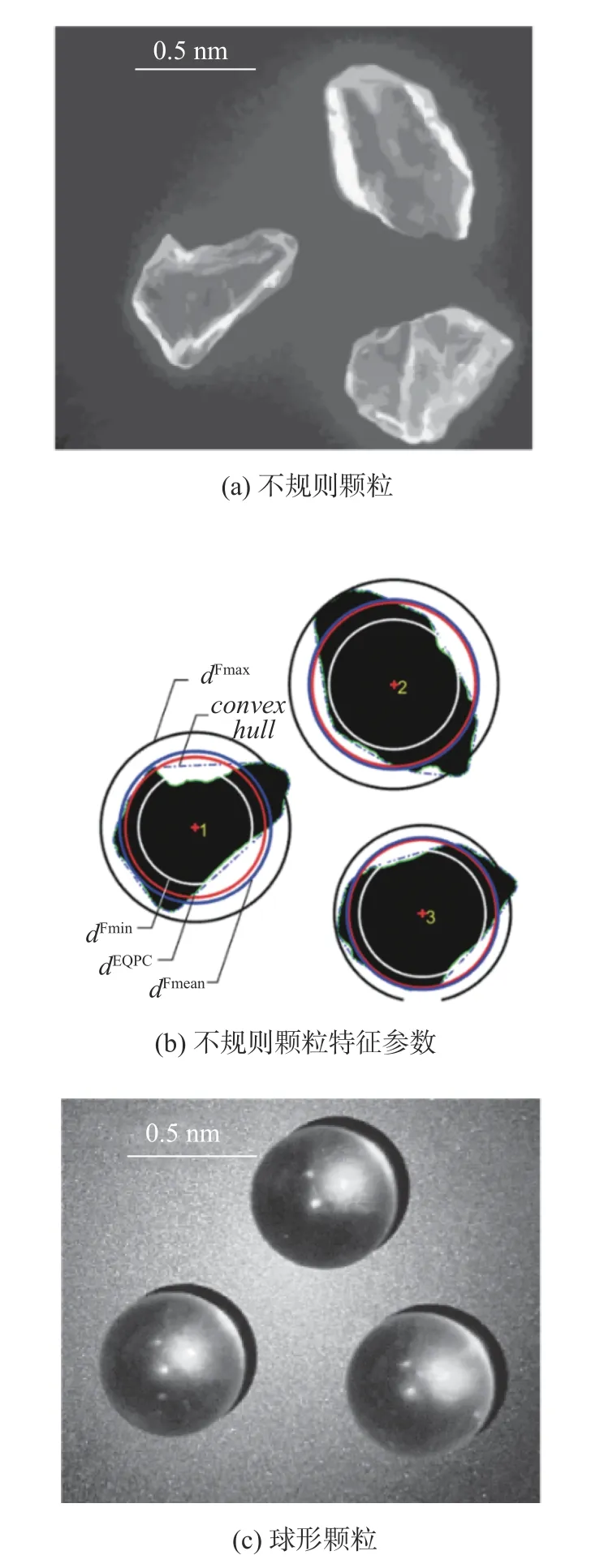
图2 颗粒图像Fig.2 Particle image

1.3 SVS测量系统

当转筒内的透明颗粒材料受到激光照射后，CCD相机能够捕捉到光子在颗粒中多次折射而形成的散射光斑。当转筒内的透明颗粒处于静止状态时，激光照射在颗粒上因散射形成的光斑也会保持静止不变。当转筒内颗粒发生雪崩运动时，散射光斑会随之发生变化，所以呈现的图像也会变得模糊，且转筒中颗粒的运动剧烈程度越高，形成的散射光斑变化也越快，捕捉到的图像也会越模糊，所以颗粒温度（δv2）就可以通过计算固定曝光时间内的一幅散射光斑图像的对比度而得到，即用所采集到的图像中散斑光强的方差除以均值，然后进行平方得到的值表示其对比度的大小[14]：

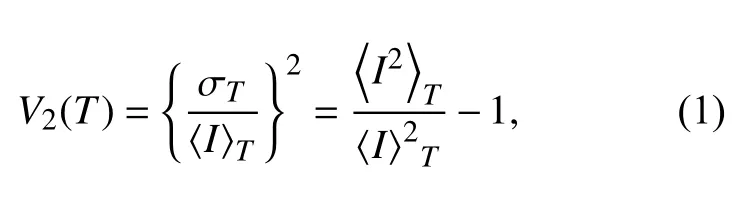
式中：T、I分别代表固定的曝光时间和散射光强度的大小；〈I〉T和σT分别为固定的曝光时间内光强的均值以及方差。散射光斑图像的对比度与颗粒温度的关系表达式则可以由高斯光束的Siegert公式[15]得到：

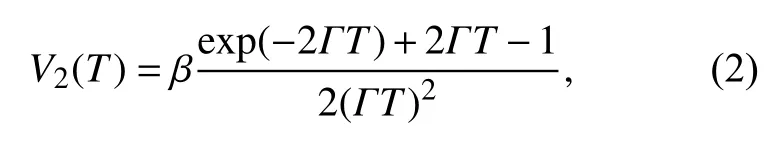
式中：β是光学系统的相干因子；Γ=4πδv/λ表示衰减线宽。因为来自外界和器材自身的影响导致无法准确测量系统中的相干因子，所以用单倍曝光时间下的散斑对比度值除以双倍曝光时间下的散射光斑的对比度值就可以消去系统β，得到颗粒温度，即

进 而根据散斑图像获得颗粒温度曲线[16]。

1.4 图像测量系统

图3为图像法测量转筒中颗粒侧面的倾斜角θ的示意图。首先，通过高速面阵CCD相机对运动过程中转筒的侧面进行采集[17]。然后，因为图片中有无颗粒的部分对比明显，所以对图片先进行自适应二值化处理，再对处理后得到的二值化图像进行斜面边缘检测，并对检测到的边缘进行拟合处理，从而得到颗粒体系的侧面基本轮廓。最后，通过识别并测量颗粒的表面轮廓获得倾斜角θ。

图3 图像法测量颗粒倾斜角示意图Fig.3 Schematic diagram of tilt angle measurement

2 结果与讨论

在间歇性雪崩运动模式下，采用高速面阵CCD相机拍摄转筒内颗粒床的侧视图，同时利用散斑能见度光谱法测量主动层的时变颗粒温 度。

2.1 不同的压实现象

图4所示为一个雪崩周期的不同时刻，转筒内颗粒床的侧视图。可以看出，两种不同形状的颗粒的雪崩运动过程是存在差异的。当两种颗粒的雪崩周期开始时，球形颗粒和不规则颗粒侧面呈现的表面轮廓虽然角度不同，但是都是直线。然而，如图4（b）所示，在不规则颗粒堆积倾斜角达到 θa2后（即t=0.66 s时），转筒中颗粒的上部表面轮廓出现拱状图像。转筒内的不规则颗粒在雪崩前其表面会形成拱形结构，称为压实[18]。实验测量到在雪崩发生前(0.12±0.02) s，不规则颗粒会以一定概率发生第二次压实现象，这是以前没有测量到的，如图4（c）所示。为了区分不规则颗粒的两种压实现象，称发生一次压实的过程为单压实现象，发生两次压实的过程为双压实现象。压实前不规则颗粒堆积的最大倾斜角称为压实临界角。图中A、B、C代表图4（a）、4（b）、4（c）三个雪崩过程中运动变化的节点，与图5中标注相对应。

图4 转筒内一个雪崩周期的不同时刻的颗粒床侧视图Fig.4 Side view of a granular bed at different times of an avalanche cycle in the drum

图5为间歇性雪崩运动过程中三种不同的颗粒温度信号。球形颗粒的间歇性雪崩运动的颗粒温度信号具有良好的周期性，如图5（a）所示。可以看出，静止时颗粒温度值接近零值。当颗粒发生雪崩运动时，颗粒温度信号发生激增，最大颗粒温度值为(3.8 ± 0.2) mm2/s2。在不同间歇性雪崩运动周期中，不规则颗粒运动的颗粒温度信号是不一定相同的。图5（b）为不规则颗粒间歇性雪崩运动的颗粒温度信号，虚线框外区域的颗粒温度信号对应于颗粒床发生单压实现象的间歇性雪崩周期，虚线框内区域的颗粒温度信号对应于颗粒床发生双压实现象的间歇性雪崩周期。可以看出，不规则颗粒在雪崩前都会发生颗粒床的压实现象。双压实现象中，第二次颗粒床的压实运动与雪崩运动的间隔时间很短，因此在颗粒温度信号中，两种信号是拼接在一起的。另一方面，压实运动的颗粒温度值明显小于雪崩运动的颗粒温度信号值。在双压实现象中，第二次压实的颗粒温度值大于第一次压实的颗粒温度值。球形颗粒未发生压实现象而不规则颗粒发生压实现象的主要原因在于球形颗粒雪崩前的体积分数不会发生变化，即颗粒间紧密程度不变，而不规则颗粒雪崩前在重力势能的影响下颗粒进行重排，颗粒排列更紧凑，从而导致体积分数减小，发生压实现象。散斑能见度光谱法具有微秒级时间分辨率，能够准确识别不规则颗粒的压实运动过程，因此在接下来的研究中，采用颗粒温度信号统计两种不同压实信号的特征。

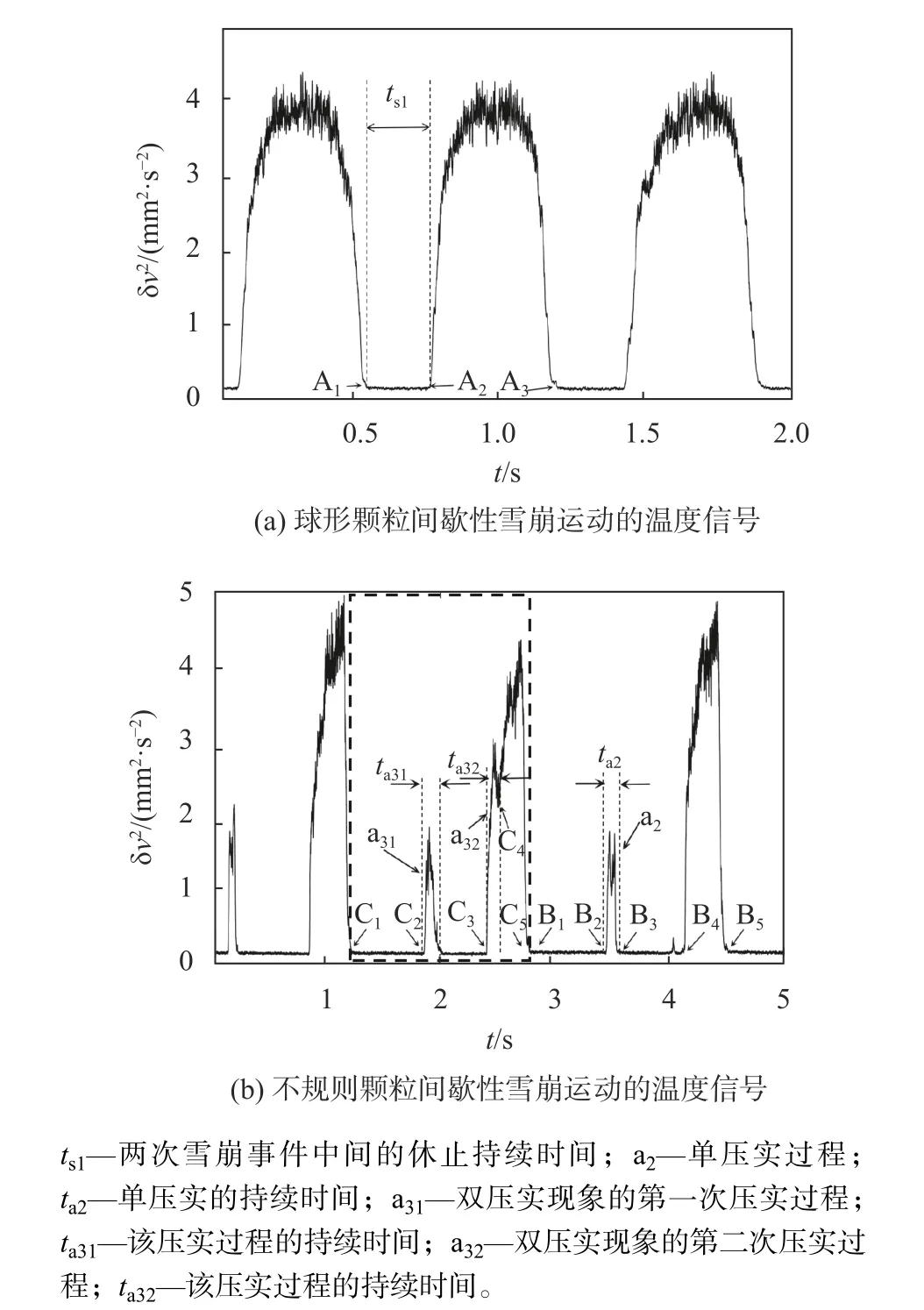
图5 间歇性雪崩运动过程中三种不同的颗粒温度信号Fig.5 Three different particle temperature signals during intermittent avalanche movement

2.2 颗粒堆积的倾斜角

图6所示为转筒内两种不同形状颗粒堆积的倾斜角随时间的变化。可以看出，在间歇性雪崩运动过程中，球形颗粒堆积的倾斜角随时间的变化规律与不规则颗粒不同，雪崩前球形颗粒堆积的倾斜角随着转筒旋转呈线性增加，而不规则颗粒的压实运动会导致颗粒堆积的倾斜角减小，并且不规则颗粒的倾斜角大于球形颗粒的倾斜角。这是由于球形颗粒间摩擦力较小且球形颗粒间不会产生咬合，而不规则颗粒之间的摩擦力较大且颗粒的不规则导致颗粒之间存在咬合，所以形成的结构更稳定，这就导致在雪崩运动过程中不规则颗粒堆积的倾斜角的变化幅值较大，且整体倾斜角大于球形颗粒。连续测量60个间歇性雪崩运动周期，获得了两种不同形状颗粒堆积的特征倾斜角，如表2所示。球形颗粒堆积的倾斜角较小，最大倾斜角θs1=26.91°±0.13°。不规则颗粒中，θc2与θc3的均值大小相等，并且θs2与θs3的大小也基本相等。说明堆积颗粒的休止角仅与颗粒材料的性质有关。比较单压实运动和双压实运动的压实临界角可以看出双压实运动的第一次压实前的临界角大于单压实的临界角，即θa31＞θa2。这一现象说明双压实运动过程中，第一次压实前颗粒堆积就存在重力势能大于单压实的情况，该现象揭示了不同压实运动可能与颗粒堆积的重力势能有关。颗粒体系内部堆积结构的不同，导致随着转筒旋转颗粒堆积的重力势能是不同的，压实前颗粒堆积的重力势能越大越容易产生双压实现象。在双压实运动中，虽然雪崩运动发生在第二次压实运动后，然而由于颗粒的压实运动会导致颗粒堆积的倾斜角减小，因此θa32≈θs3。

表2 转筒内两种不同形状颗粒堆积的倾斜角Tab.2 The tilt angles of two different shapes of grain accumulation in the drum

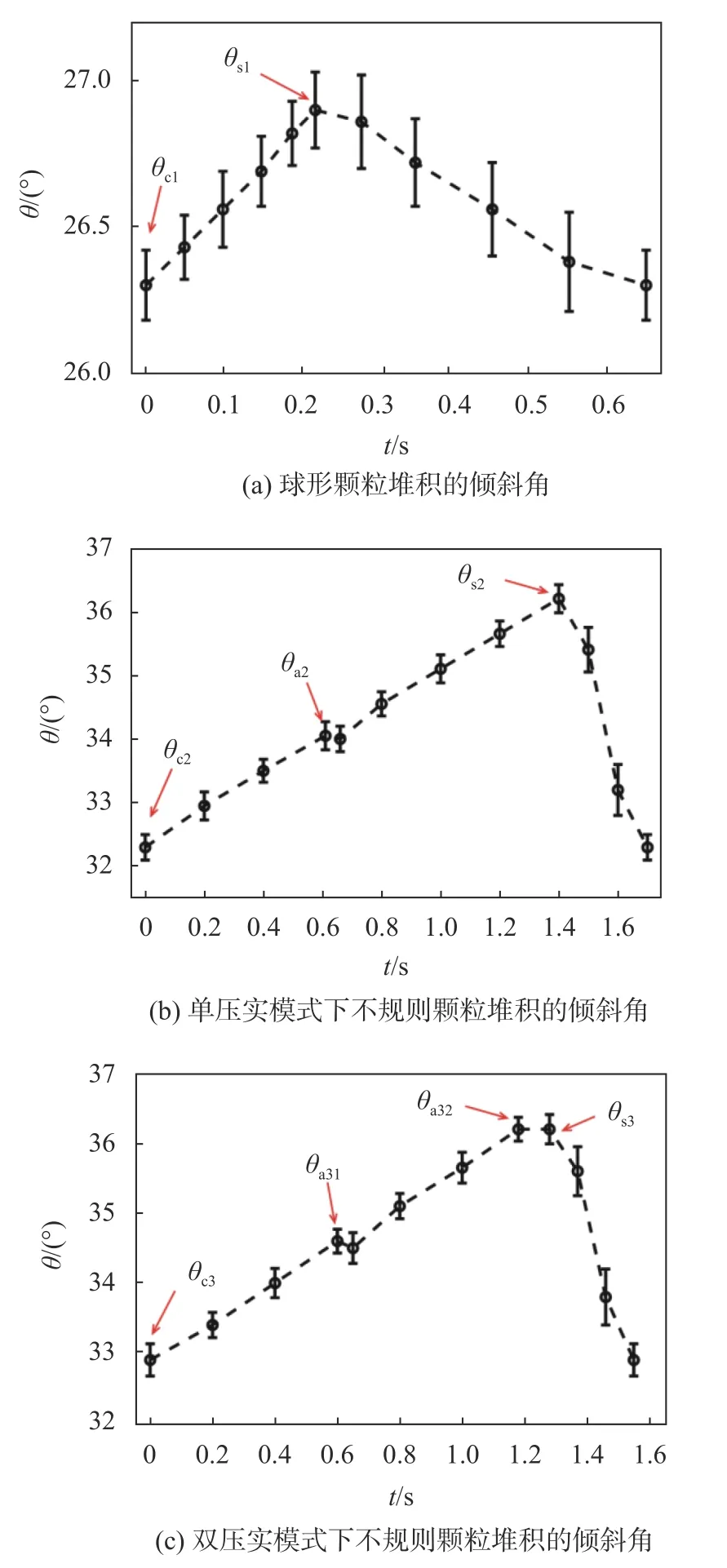
图6 转筒内两种不同形状颗粒堆积的倾斜角随时间的变化Fig.6 The tilt angles of two different shapes of grain accumulation in the drum varying with time

2.3 填充度对压实运动的影响

在不规则颗粒间歇性雪崩运动的过程中，颗粒的单压实现象与双压实现象是随机发生的。为了揭示发生不同压实运动的规律，确定发生概率，定义P为双压实现象出现的概率，则

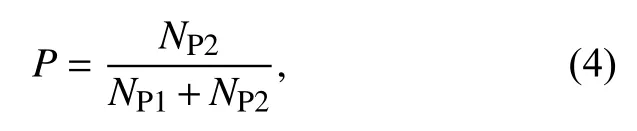
式中：NP1为发生单压实现象的次数；NP2为发生双压实现象的次数。图7是不同填充度条件下，不规则颗粒发生双压实现象的概率分布图。在相同填充度条件下，统计了300个间歇性雪崩周期。可以看出，双压实现象受到颗粒填充度的影响。在填充度为15%至35%时，颗粒发生双压实运动的概率大于60%。而在其它填充度条件下，发生双压实运动的概率下降至20%以下。

图7 不同填充度条件下不规则颗粒发生双压实现象的概率分布Fig.7 Probability distribution of double compaction of irregular particles under different filling conditions

图8是不同填充度条件下，不规则颗粒压实持续时间的变化曲线。在相同填充度条件下，统计了300个间歇性雪崩周期。可以看出，单压实的持续时间随着填充度的增加而缩短，压实持续时间大于0.15 s。双压实运动中，两次压实运动的持续时间呈反比例关系。第一次压实运动的持续时间随着填充度的增加而增长，而第二次压实运动的持续时间随着填充度的变化规律与单压实运动相同。另一方面，压实运动的持续时间均大于0.08 s。这表明压实运动导致颗粒重排需要一定的弛豫时间。

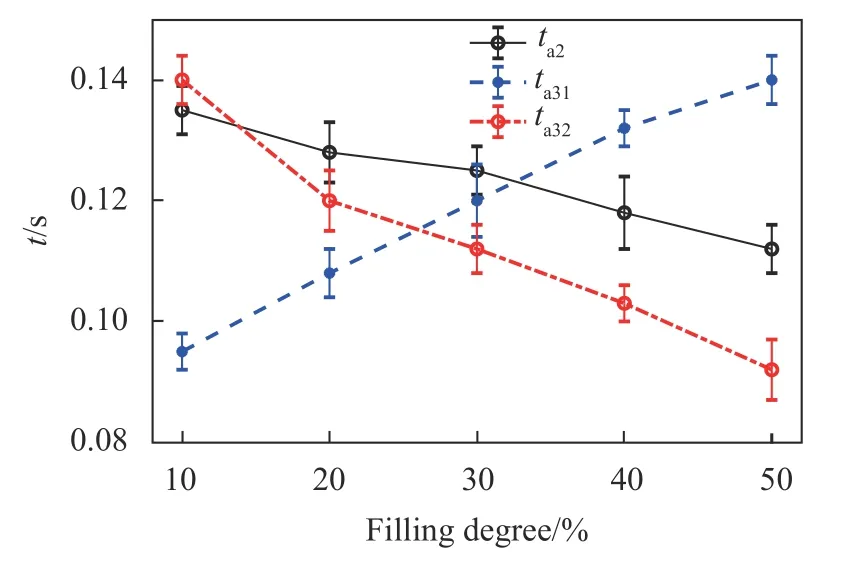
图8 不同填充度条件下不规则颗粒压实持续时间Fig.8 Duration of irregular particle compaction under different filling conditions

3 结 论

本文在转筒转速为0.007 5 r/s不变，转筒内颗粒的填充率改变的条件下，选用粒径均为0.5 mm的球形和不规则玻璃颗粒，利用SVS和图像法相结合的手段，观察转筒内颗粒运动状态变化。通过测量颗粒的倾斜角与颗粒温度，得到如下结论:

1）球形颗粒和不规则颗粒的雪崩模式存在差异，球形颗粒的雪崩模式相同，而不规则颗粒则会在雪崩前产生单压实和双压实两种不同的雪崩模式；

2）不规则颗粒的倾斜角大于球形规则颗粒的倾斜角，并且不规则颗粒雪崩前的倾斜角越大，其发生第二次压实的概率越大；

3）不规则颗粒的填充度不同，其发生双压实的概率也不同，填充度在15%～35%之间出现双压实的概率较大，并且单压实和双压实的压实持续时间的变化趋势也不同。