数值差分算法在静电场模拟实验中的设计与应用
翟立朋,常凯歌*,程 琳,张俊武,童 童
(1.西安交通大学 物理学院 物理国家级实验教学示范中心,陕西 西安 710049;2.西安工程大学 理学院,陕西 西安 710048)
模拟法描绘静电场是普通物理实验中电磁学模块的一个核心实验。带电体在其周围产生的静电场可以通过电场强度E或电势φ的空间分布来描述。对类似于同轴圆柱、圆筒这样的规则电极,可以根据已知的电荷分布用静电场方程求得电势和电场分布的解析解。而对于不规则电极来说,电势和电场分布的数学求解十分困难,需要用实验方法进行测量[1]。
模拟法本质上是通过一种容易实现、便于测量的物理量和物理过程,去代替不容易实现的、不便于测量的物理量和物理过程[2,3]。静电场模拟实验通过测量相对容易的恒定电流去实现对静电场的测量,因为静电场中没有电流不能使用电磁式仪表进行直接测量,同时探测装置必须是导体或电介质,一旦将其放入静电场中,将会产生感应电荷引起电场畸变,影响测量结果的准确性。恒定电流之所以能模拟静电场是因为电流J和电场E有相同的物理表达形式[4]。近年来,针对模拟法测量静电场实验的数据处理方法[5,6]、仪器改进[7-9]、误差分析[10,11]、教学方法[12,13]与测量手段[14,15]的创新等都已经有了很好的研究,但实验模型仍然局限于研究同轴圆柱、圆筒电极间的静电场。在普通物理实验上对于不规则电极,一般只测量其等势线,再根据等势线与电场线的关系得到电场线的分布定性的画出电场线,无法真正得到静电场的具体数值。
随着计算机信息技术的发展,数值方法越来越多地被应用到教学和科研中来。实验也可以使用COMSOL、Ansys、FDTD Solution等成熟的商业软件进行仿真分析[16,17],但商业软件往往费用昂贵并且学生在使用商业软件的过程中往往无法完整理解其仿真算法,所以不太适合在大面积基础物理实验课程中进行推广。基于MATLAB将数值差分算法应用到静电场模拟实验中,可以给出任意形状电极静电场、电荷的分布图,一方面扩展了该实验项目的应用场景,更重要的是将科研思维和方法应用到物理实验教学中,可以大面积在基础物理实验课程中推广应用。
1 模拟静电场的基本原理
由电磁场理论可知[4],均匀导电介质中稳恒电流所产生的电流场与均匀电介质中的静电场具有相似性,这两种物理场所遵循的物理规律具有相同的数学形式。对于静电场而言,当介质中没有自由移动的电荷时,电场强度矢量E满足方程:
(1)
∮lE·dl=0
(2)
对于稳恒电流,当介质中无电流源时,电流场中的电流密度矢量J满足方程:
(3)
∮lJ·dl=0
(4)
由此可见E和J在各自区域中满足同样的数学规律[1-3]。并且这两个物理量都与电势φ之间有着内在的关联,所以在实验上由直流电路构建一个稳恒的电流场,通过测量电极之间电势差得到电流场的分布,进而替代静电场的分布。

图1 同心圆柱、圆筒电极的实物与模型图
如图1所示,为无限长且同轴的圆柱和圆筒电极的横截面,圆柱A和圆筒B分别作为正、负电极,并设定圆筒B的电势为零,即φB=0。rA和rB分别表示圆柱和圆筒的半径,如果以圆柱A的圆心为坐标原点,则A、B之间位于r处的电势可以通过高斯定理[3]得到:
(5)
静电场是电势的负梯度,电势φr对位置r取导数,就可以得到任意位置处的电场强度表达式:
(6)
所以,只需要将A、B两端电极加上稳定的电压,测量电路中不同位置处的电势即可得到φr的具体数值,根据位置信息可以计算得到具体的电场强度值。
为了满足上述理论中的需求,在实验上使用如图2所示的电路在A、B两个电极之间加一个可调电势差。电极之间的灰色矩形框代表导电微晶,导电微晶是一种电阻分布均匀的导体,移动电势探头的位置,电压表的读数即为电极B与探头之间的电势差,如果设定电极B的电势为零,则电压表可以测量任意位置处的电势。

图2 模拟静电场实验电路图
但是遗憾的是,实验虽然可以计算得到电场强度,但是得到电场强度的数值的方法与各个位置处的电势没有关系,在教学过程中体现不出模拟法具体应用;更重要的是实验虽然可以测量任意形状、任意位置处的电势,但在理论上只能对同轴的圆柱、圆环模型进行解析计算,其他形状的电极无法给出类似于公式(6)这样的解析表达式。所以,设计并应用数值差分方法,将实验推广到任意电极情况下的静电场模拟。
2 数值差分算法及可行性验证
如果可以得到电势随位置的变化关系图像,根据电磁学理论可以计算电场强度的大小。对于任何形状的电极,电场强度为电势的负梯度,这是恒定成立的,即:
E=-∇φ
(7)
对于如公式(5)所示,电势有解析表达式的电极模型,通过公式(7)可以计算得到电场强度的解析表达式。而对于不规则电极,引入数值差分算法对公式(7)进行求解。
在上述同心圆柱、圆筒模型中,电势沿着径向成空间一维分布。对于梯度差分来说,数值差分算法的第一步是将位置空间进行离散化,所以首先需要的是将位置r每间隔Δr进行划分,这样空间的任意位置都可表示为:
r=n·Δr
(8)
其中n非负整数,根据对空间位置的离散划分,任意位置处的电势可表示为:
φr=φ(n·Δr)
(9)
在完成第一步空间离散化以后,第二步需要将电势对空间的微分近似为差分,电势的梯度表示为:

(10)
微分与差分的区别在于极限Δr的取值精度,Δr取值越小极限精度越高。所以,只要能保证离散空间Δr足够小,就可以保证差分算法的计算结果足够精确。当然Δr不能无穷小,否则也无法进行计算机的仿真计算。可以不局限于特定的电极模型,将任意位置处的电场强度表示为:
(11)
这样不需要解析解也可以描述出任意位置处的电场强度。
为了验证该方法的可行性,使用GVZ-4型静电场描绘仪对同轴圆柱、圆筒模型进行测量和计算,分别通过解析算法和数值差分算法对电势、电场的测量和计算结果进行对比分析。调节电路使电极A、B的电势分别为φa=10.00 V、φB=0.00 V。该模型中同心圆柱的半径为ra=1.0 cm,同心圆环的内径为rB=6.4 cm,将参数带入到公式(5)和公式(6)可以计算得到A、B之间任意位置处电势的解析表达式为:
φr=10.00-5.39·lnr
(12)
可以看出φr与lnr之间满足线性关系。得到A、B之间任意位置处电场强度的解析表达式为:
(13)
实验上用图1所示的电极模型,测量过程中使用的位置差分间隔为Δr=0.2 cm,将测量得到的电势值代入公式(11)得到对应位置处的电场强度值,测量得到各个半径r处对应的电势和电场强度数值如表1所示。需要说明的是电场强度是相邻两个电势做差之后计算得到,差分之后的电场强度数据量要比原始的电势数据少一个,所以表1中r=1.2 cm处没有电场强度值。

表1 同轴圆柱圆筒电势与电场值
如图3(a)和(b)分别表示同轴圆柱圆筒模型中电势和电场强度值随着位置的变化关系,图像中的直线与曲线代表的是理论值,图3(a)中的散点代表的是电势的测量值,图3(b)中的散点代表的是经过差分公式计算得到的电场值。

lnr/cm(a)
可以看出电势测量值以及经过差分计算的电场值与理论值吻合非常好。
进一步计算得到电势测量值的标准偏差为:
(14)
其中φi和φ0分别表示对应位置处电势的测量值与理论值。差分结果与理论值之间的标准偏差为:
(15)
图3所展示出的关系图以及标准偏差,都说明了该方法在模拟静电场实验中是可行的。
对于其他形状的电极来说,需要建立二维空间直角坐标系,可以通过如图2所示的电路测量得到二维空间的电势分布φ(x,y)。二维空间离散化以后任意空间位置可以表示为x=m·Δx、y=n·Δy,则电场强度的分布就可以表示为:

(16)
(17)
在得到电场分量得到以后即可得到电场强度的绝对值:
(18)
该算法不仅可以计算任意形状的电场分布,进行二次差分以后,还可以得到空间电荷分布。根据高斯定理,空间任意位置处的电荷分布可表示为:

(19)


(20)
(21)
将(20)、(21)两式代入到公式(19)以后,就可以得到空间任意位置处的电荷分布,这样只要测量得到任意电极模型的电势分布,静电场的电场强度、电荷等参量即可全部得到。
3 任意形状电极电场与电荷分布
如图4所示,为GVZ-4型静电场描绘仪中的一种四电极模型,并建立如图所示的xoy坐标系,坐标系中导电微晶上每一个最小网格为:Δx=0.2cm、Δy=0.2cm,以此为离散空间的大小。下面两个电极都接电路中的B电极,这两个电极的电势都为φB=0.00V,上面两个电极都为A电极并设定电势为φa=10.00V。

图4 四电极模型的结构图与坐标系
每间隔0.2cm测量各个位置上的电势以后,就可以得到如图5所示的电势分布图,图中每条曲线及对应的数值代表等势线及对应的电势值。从等势线可以清晰地看出电极轮廓及二维平面上的电势分布。因为电极都是金属导体,从等势线也可以看出四个电极都为等势体,下面两个电极电势为0.00V,上面两个电极电势为10.00V,这都符合实验设定的初始条件。

图5 四电极模式的电势分布
测量得到二维电势分布以后,使用MATLAB对二维数据进行差分运算,MATLAB差分计算的整体模型和流程如图6所示。
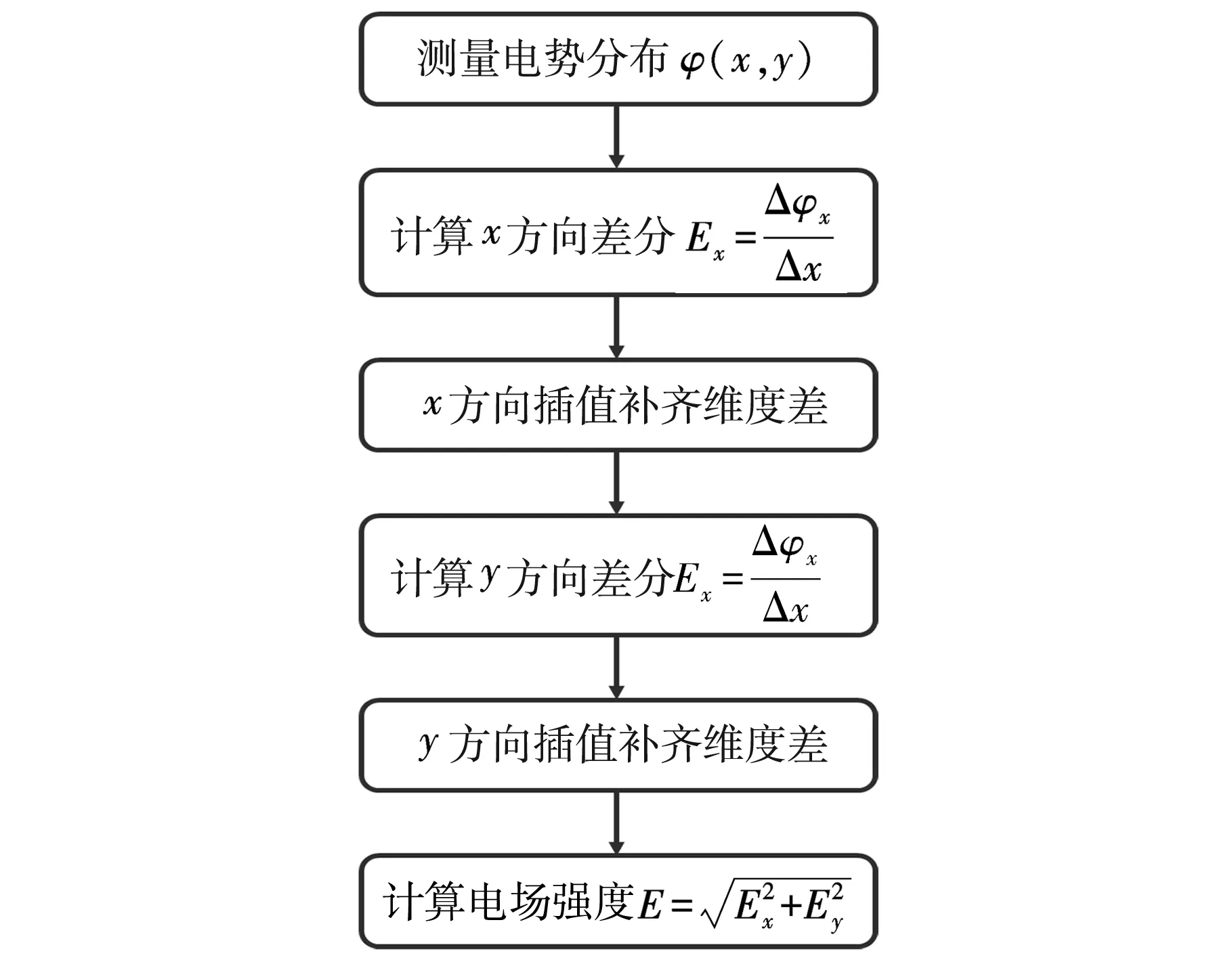
图6 MATLAB数值差分计算模型
分别将二维电势分布在x方向和y方向进行差分和插值,这里需要插值补齐是因为经过差分运算以后会有数据损失,例如在表1中电势值有27个数据,但是差分之后r=1.2cm处就少了一个电场数据,电场强度只有26个数据,需要经过插值运算将26个数据补齐到27个,计算得到的电场和电荷分布都使用的是三次样条插值算法。
如图7所示的电场分布可以看出,强电场主要分布在A、B电极之间,同A电极或同B电极之间的电场强度较小。电极附近尖锐位置处的电场强度较强,符合尖端效应的预期。

图7 四电极模型电场强度分布
图8所示的电荷分布中红蓝色分别代表正负电荷,白色区域代表无电荷分布,可以看出大量电荷主要分布在电极导体表面以及导体尖端处,导体内部无电荷分布与静电屏蔽原理吻合,导电微晶平面上分布有少量负电荷,每两个同A电极或同B电极之间的正负电荷都成对称分布,说明这是在同电极之间两个不同位置处形成了偶极子。
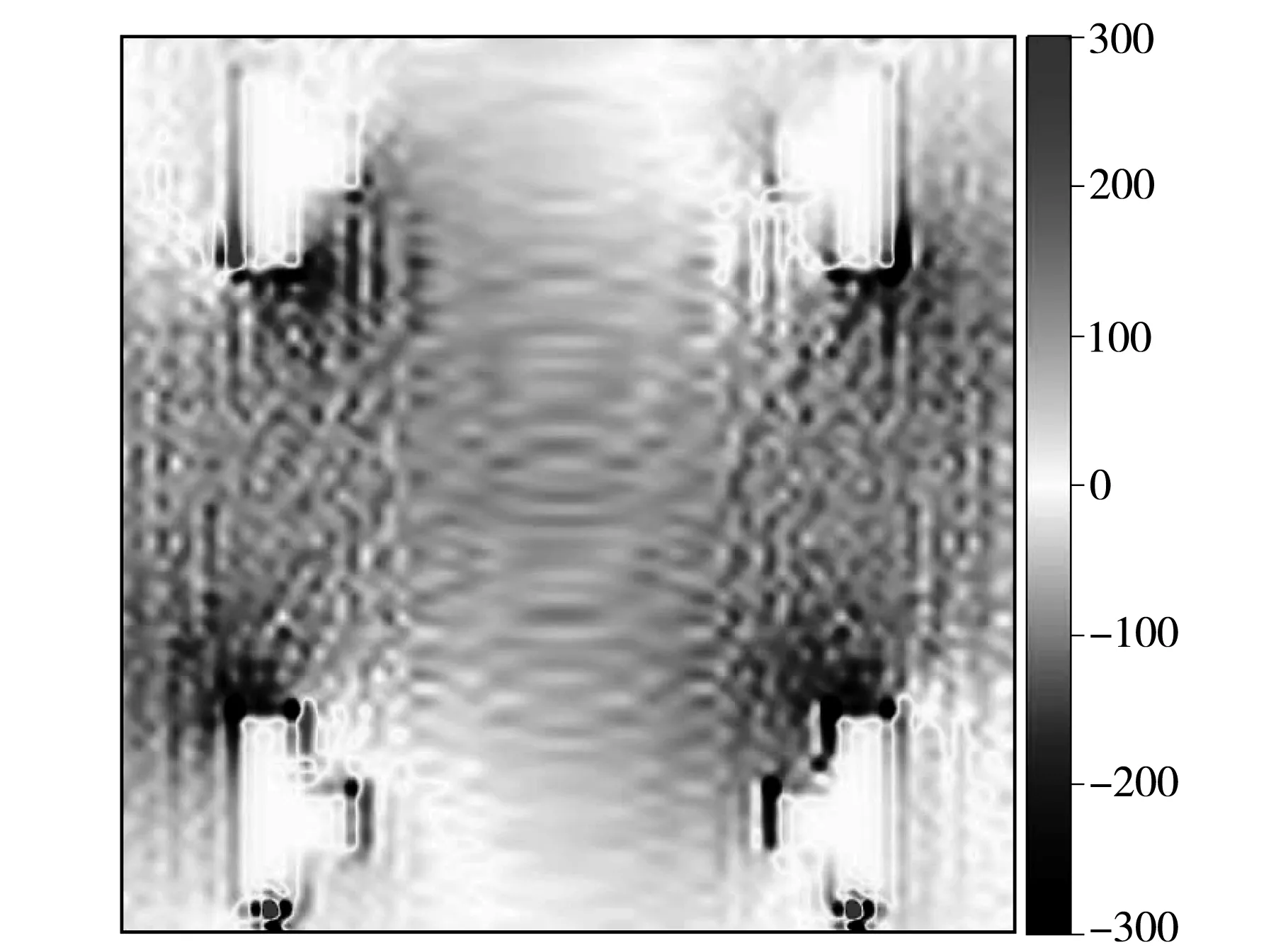
图8 四电极模型电荷分布
4 结 语
将数值差分算法引入到模拟静电场实验中,实现了电场强度分布和电荷分布的测量,弥补了该实验项目没有完全测到电场数值的欠缺,虽然只给出了一种四电极模型的电场、电荷分布情况,但方法可以应用到任意形状的电极模型,这对实验内容的深度和广度是非常有效地拓展。

