大挠度压电聚合物薄膜的能量收集研究*

王乐生， 王海峰， 王世龙， 孙凯利

(青岛大学 机电工程学院，山东 青岛 266071)

0 引 言

随着压电俘能技术的不断发展，压电材料的种类也不断增多。一般来说，压电材料按其组成部分可分为刚性压电陶瓷和柔性压电聚合物。其不同之处在于变形程度和发电量。其中，压电陶瓷[1,2]具有较高的压电应变常数，但变形小，易损坏;压电聚合物主要由长链聚合物组成，其压电应变常数小于陶瓷型。与其他流行的压电材料不同，聚偏二氟乙烯(polyvinylideme,PVDF)薄膜具有较高的柔韧性，容易弯曲，适合在低频环境振动中长期获取能量[3,4]。2001年，泰勒等人[5]发明了一种名为“能量收集鳗”的新装置，它利用PVDF将海洋和河流中的机械能转换为电能。Akaydin H D等人[6]通过研究在高雷诺数的湍流边界层放置柔性压电悬臂梁来产生电压。Pankonien A M和Ounaies Z[7]开发了压电活性海带系统，它由化学惰性压电聚合物或压电陶瓷制成的柔性长带。当由波浪产生的周期性洋流经过该系统时，会带动长带进行往复的机械运动。压电材料通过压电效应将这种机械运动直接转换为电能。唐火红等人[8]利用PVDF的压电特性研究了一种用于采摘果实的机械手,当PVDF受到应力发生形变时，由于压电效应，其表面会产生电位差，从而产生电压，通过电压的变化来完成采摘工作。Orrego S等人[9]探究了通过固定在称为“倒置标志”的新方向的柔性压电膜的自激振动(颤振)来收集风能的实验研究。研究得出即使在低风速状态下，也能收集0.4 mW/cm3的发电量。

本文研究了大挠度变形下的PVDF薄膜产生能量情况，并分析了其低频振动的发电问题。利用压电本构方程，推导出弯曲PVDF板的输出电压和电流。最后通过对三种不同尺寸的PVDF薄膜进行数值分析，比较它们在大挠度

条件下的能量采集特性。为研究相关领域的科研人员提供了理论数据。

1 压电理论

压电耦合由机械应力矢量T，应变矢量S与电位移矢量D，电场矢量E的线性压电本构方程来描述

S=sET+dE,D=dtT+εTE

(1)

式中sE为恒定电场下的柔度矩阵;d为与应变场相关的压电矩阵;dt为d的转置项,是恒定应力下的介电矩阵。d项为机械部件和电气部件之间完全耦合。如果将d从式(1)中去掉，则只剩下未耦合的胡克定律和麦克斯韦方程。

压电材料一般有三种模态，即33模态、31模态和15模态。本文仅用31模态分析压电单模态和双模态的特性。31模态是指电压作用于3个方向(即材料极化为3个方向)，机械应力作用于1个方向。在31模态下，一个方向上受到应力会产生应变，导致薄的压电元件弯曲变形，从而产生电压[10,11]。对于双模态，2个单独的薄片粘接在一起，有时中间有1个中心垫片。当元件弯曲时，上层受拉底层受压，反之亦然。如果每一层电极在相同的方向上，并且连接正确，每一层产生的电流将会增加，称为平行极化。相反，如果在相反的方向极化，电压将增加，称为串联极化。如图1所示,在31模态下，由于压电板受到Z方向的力，在压电板板内产生横向应力T1,电场分布E3和电位移D3,从而产生电压V。

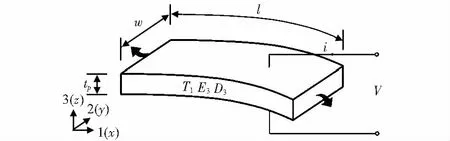
图1 压电板横向31模态

如果忽略y，z方向应力的影响，压电本构方程(1)可简化为

(2)

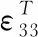
为了得到电荷Q,电压V和应力分布的关系，需要对式(2)进行体积积分

(3)

式中A为电元件的电极面积，Ψ为压电元件的体积。

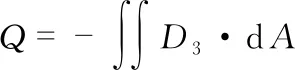
(4)

(5)

将式(3)改写为

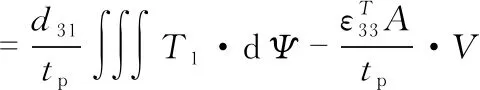
(6)

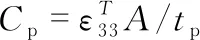
(7)

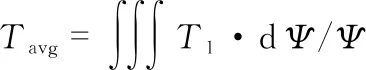
2 实验研究

2.1 PVDF俘能器性能

因其具有良好的弹性，可承受较大的载荷应变，故采用PVDF压电薄膜。其元素特性如表1所示，主要物理参数如表2所示。

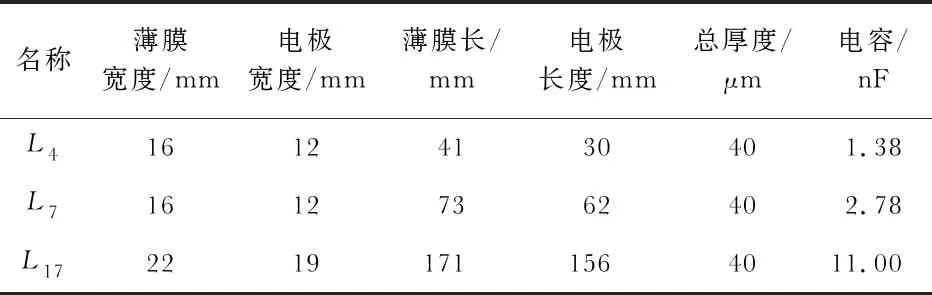
表1 PVDF压电薄膜元素特性

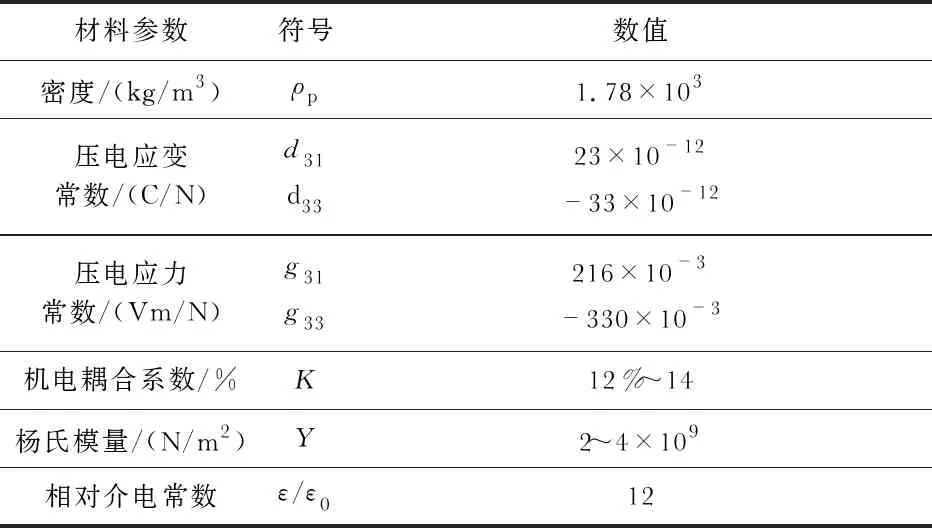
表2 PVDF薄膜的物理参数

2.2 实验方案

为了研究PVDF薄膜的变形情况对发电的影响，测试了3种不同长度的薄膜，分别为4.1 cm (L4)，7.3 cm (L7)和17.1 cm (L17)。由压电薄膜的长度L和位移D控制，利用这两个参数比较了不同长度压电薄膜的位移和性能。例如，L-D=17.1-14表示PVDF膜长L=17.1 cm，自由端位移D=14 cm。如图2所示，压电薄膜的电极端安装在固定端架上，另一端放置在自由端架上，自由端在极低频摆动。在接下来的试验中，比较了不同长度压电薄膜的位移距离和发电量。

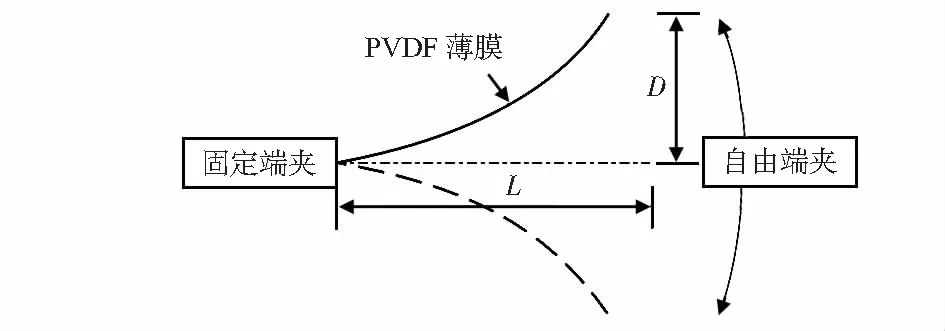
图2 PVDF薄膜摆动的实验方案模型

2.3 实验结果

在PVDF薄膜的长度一定时，可以通过改变位移(D)来探究位移对发电能力的影响。将L17类型的PVDF薄膜的位移D从2 cm增加到16 cm，每次增加间距设为2 cm，以原点为固定端，不同位移大小的PVDF薄膜的形变情况如图3所示。

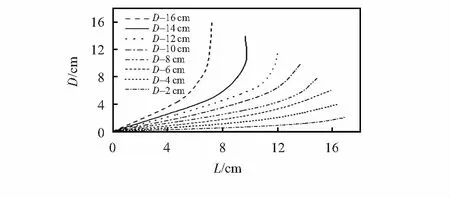
图3 L=17.1 cm时PVDF薄膜的不同位移下的形变

从图3可以看出，当D=14 cm时，压电薄膜的整体形变量最大。分析结果表明，电压随位移的增大而增大。但当D超过14 cm时，电压下降。因此当D=14 cm时，PVDF薄膜的输出功率最大。用同样的方法对另外两种PVDF薄膜进行了测试。因此，可以将三种不同长度的PVDF薄膜(L4,L7和L17)的计算功率结果放在一起讨论。表3给出了三种PVDF薄膜的位移、输出电压和功率之间的关系。

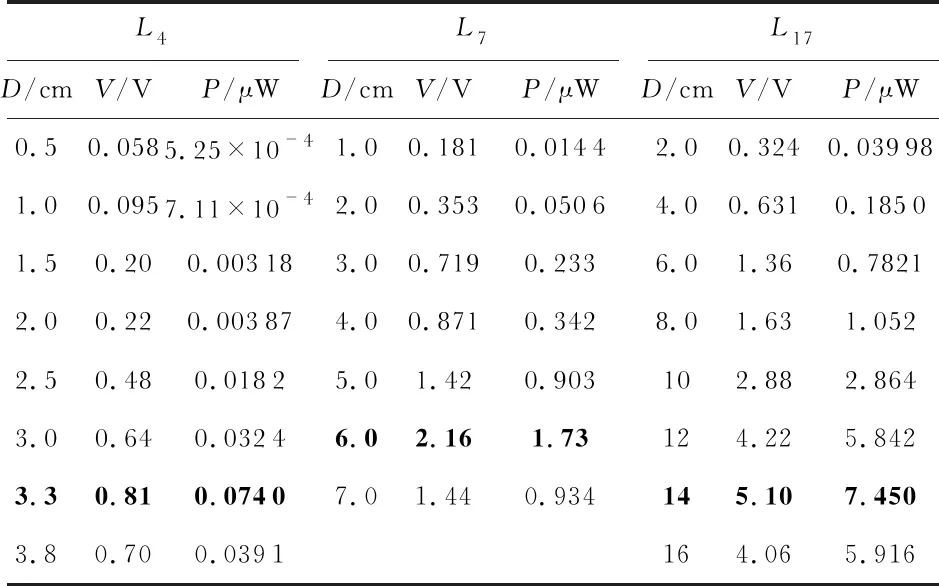
表3 位移、输出电压和功率之间的关系

三种PVDF薄膜的位移、长度和输出功率的关系如图4所示。其横轴定义为薄膜的位移与长度之比，即D/L。结果表明当比值为0.81时，功率输出最高。最大输出功率与表3中加粗的结果相匹配。

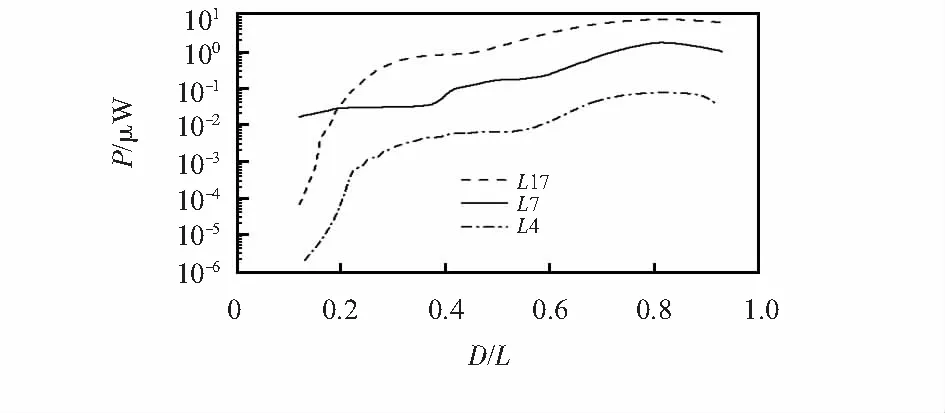
图4 位移/长度与输出功率之间的关系

将PVDF薄膜的摆动时间与摆动周期的比值定义为无量纲时间(Td)，分别对三种不同长度的PVDF薄膜在D/L=0.81时进行分析，分析得输出电压(V)、电流(I)、功率(P)在无量纲化时间上的变化分别如图5所示。

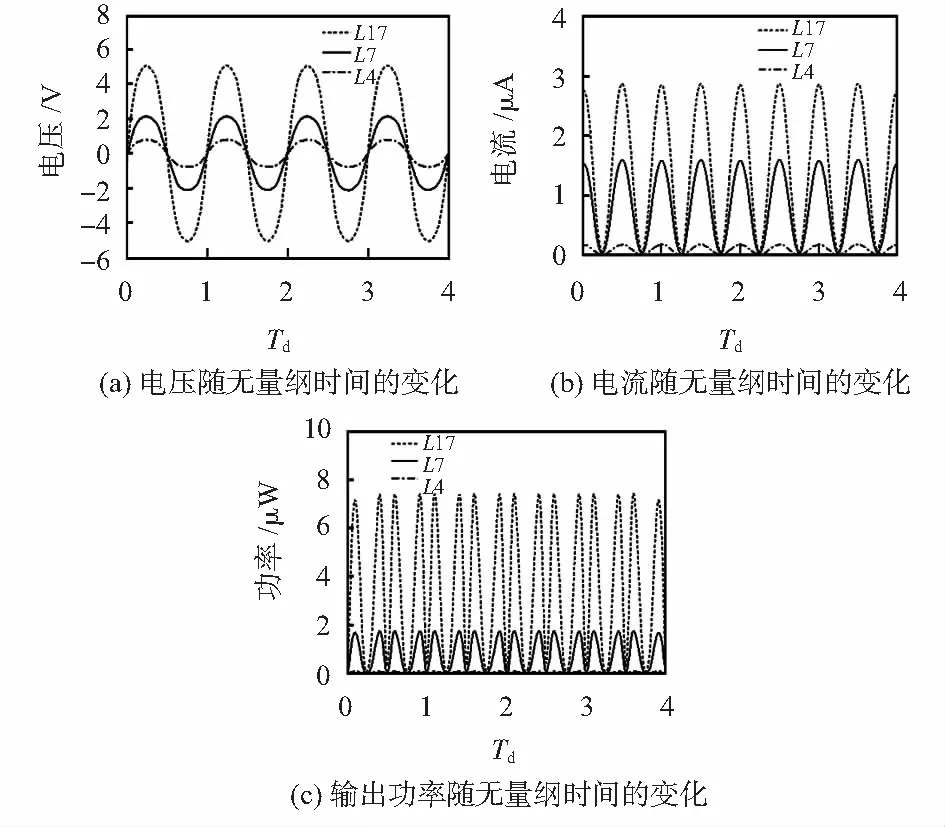
图5 电压、电流、输出功率随无量纲时间的变化

如图5(c)所示，将图5(a)所示的输出电压与图5(b)所示的电流相乘，得到不同长度的PVDF薄膜的输出功率，由于最大速度和瞬时位移的影响，其在电流的1/4个周期时达到最大输出功率。三种长度的PVDF薄膜的最大输出功率如表4所示。

表4 最大输出功率比较

3 结 论

本文讨论了大挠度压电聚合物薄膜的能量捕获特性。有限元分析结果表明：在长度为4.1,7.3，17.1 cm的三种PVDF薄膜中存在着共同的现象，当位移长比接近0.81时，输出功率最好。对于长度为17.1 cm的PVDF膜，当位移达到14 cm时，其最佳输出功率为7.45 μW。但如果位移超过14 cm，电压和功率下降。目前PVDF薄膜的单片输出能量较小，采用串并联组合阵列可以提高能量采集水平。