P300信号分类的多样本融合支持向量机算法

范 玮，罗思吟，邓轶赫，王 炜，李圆媛

武汉工程大学数理学院，湖北 武汉430205

脑电信号是大脑细胞器进行生命活动所产生的一种电活动，其产生的方式主要分为诱发脑电信号以及自发脑电信号两种方式。诱发脑电信号是指因外界某种刺激使大脑电位产生变化从而形成的一种脑电活动。脑电信号由人体皮层内的大量神经元突触后电位同步总和而形成［1］，是许多神经元共同活动的结果，包含了大量与人体生理和疾病有关的信息，为康复治疗提供了有效的帮助。在临床医学领域中，脑电信号不仅作为某些脑疾病的临床诊断依据，同时还作为一种辅助治疗手段帮助一些脑疾病进行康复治疗。在工程应用中，利用脑电信号实现的脑机接口，为瘫痪病人的某些功能重建提供了一种有效的方法。因此在康复医疗领域的实际运用中，对脑电信号的深入研究具有重要意义。

基于事件相关电位的脑机接口通常使用的是P300信号，P300信号是由人脑在受到小概率刺激后300 ms左右出现的一个正向波峰［2］。P300电位作为一种内源性成分，通常与刺激物理特性无关，而与知觉或认知心理活动有关，并与记忆、智能、注意等加工过程密切相关。基于P300的脑机接口优点在于它具有稳定的锁时性和高时间精度特性，研究人员无需复杂训练就能够获得较高的识别准确率。对脑机接口所获得的电信号进行P300电位的自动化识别也成为了脑电信号研究领域的关键研究之一［3］。

本文针对脑机接口所获得的电位波形进行了P300电位的分类识别研究，采用了多样本融合的支持向量机（support vector machine，SVM）算法对脑电信号进行分类识别并与单样本的SVM算法进行了比较。

1 实验部分

1.1 实验方法

P300信号无需对受试者进行预先训练，只需要通过视觉刺激的方式使其自发产生。实验设计如表1所示，该实验可设计为一个6行6列的字符矩阵。首先，提示受试者注视屏幕上的“目标字符”，假设出现的“目标字符”为“A”，在受试者注视“目标字符”的过程中，当给定的“目标字符”所在行或列闪烁时，P300电位就会在受试者的脑电信号中出现；相反当其他行或列闪烁时，P300电位则不会出现在受试者的脑电信号中。其次，字符矩阵每次将以随机的顺序闪烁字符矩阵的一行或一列，每次闪烁80 ms，两次闪烁之间间隔80 ms。如若所有行和列均闪烁过1次，则本轮实验结束，并开始下一轮试验，该实验共重复5轮。脑电信号在采集过程中使用了20个通道，采集频率为250 Hz。

表1 行/列的标识符Τab.1 Row/column identifier

P300电位分类识别的目的即为判断某行或列闪烁后，脑电信号中是否出现了P300电位。该实验本质上是一个二分类问题，因此非常适合使用SVM算法解决。

1.2 实验数据采集

研究数据来自于5名健康成年被试者，平均年龄为20岁，均采用前述的实验方法，每个字符都进行5轮矩阵闪烁实验，因此每个字符闪烁实验都含有60次闪烁数据。本研究共收集了12个已给出目标字符的训练用数据，以及10个未给出目标字符的待识别目标字符数据用于测试，每个字符闪烁实验的数据为：

表2 通道与数据特征对应关系Τab.2 Correspondence between channelsand features

图1 脑机接口采集设备中各通道位置示意图Fig.1 Position of each channel in brain-computer interface acquisition device

1.3 数据预处理

数据中的噪声和其他质量因素都会直接影响算法的识别效率，有必要对原始数据进项预处理操作，主要过程如图2所示。首先采用8阶的切比雪夫低通滤波器对每个脑电信号采集通道的信号都进行阈值为10 Hz的低通滤波处理，仅保留频率低于10 Hz的部分。

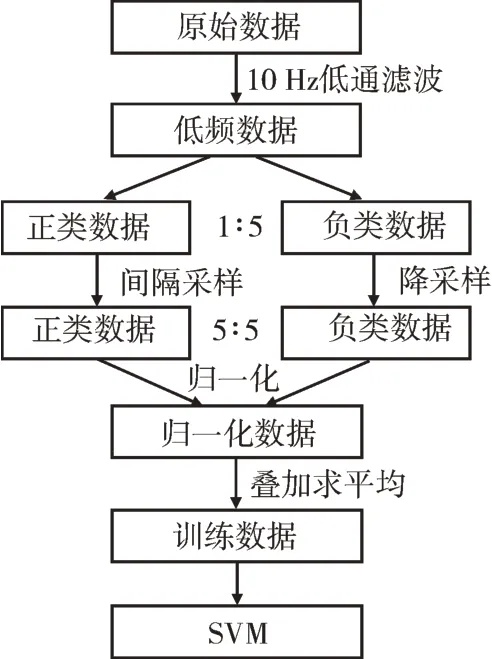
图2 数据预处理流程Fig.2 Flowchart of data preprocessing

接着考虑到P300电位一般在刺激之后的300 ms左右产生［4］，为了尽可能地包含P300电位的产生时间段，本研究从数据中提取出持续时间800 ms的单次试验数据段，对应200个采样点，根据每次试验对应的字符，将该字符对应的行列的试验数据段标记为含有P300信号的正类数据（类别标记为+1），其他实验数据段标记为不含P300信号的负类数据（类别标记为-1）。

数据通过切比雪夫滤波后需要进行降采样，对每条实验数据段进行间隔为5个的降采样，这样单次实验的采样点数降为了40个。同时由于每轮实验含有对应字符和行列数仅占总行列数的1/5，即正类数据与负类数据样本数量比值为1∶5，类别数量的不平衡会极大地影响到分类模型的训练和误差计算［5］，因此要对含有P300信号的数据样本进行数量上扩充，具体扩充方法利用了降采样过程针对含有P300信号的正类进行起始索引的不同的5次间隔降采样，这样就得到5条含有P300数据的原样本的过采样数据。上述过程能够获得类别比例为1∶1的两类数据，避免了类别不平衡的问题。

然后针对每个试验数据段所包含的采样数据，按最大最小归一化处理，使用线性化的方法将原始数据转换到［0，1］的范围内。

最后为了有效地突出P300信号和提高分类性能，针对每个待确定字符的5轮测试数据，按照行列序号对每个行列对应的5轮采样数据分别进行了叠加求平均的操作，获得每个待确定字符测试数据中12个不同行列对应脑电波平均波形，并且也进行了可视化展示，如图3所示。从图3中可以发现有P300信号的平均波形在300～500 ms之间，有明显的正向波峰，符合P300信号的特征。

图3 有P300信号和无P300信号的平均波形对比Fig.3 Comparison of average waveforms with P300 signal and without P300 signal

经过上述操作后，单个字符测试试验中的60条有效数据合并为12条，12个目标字符的实验数据最终对应144条训练数据，10个目标字符的检测数据对应120条检测数据。

1.4 多样本融合的SVM算法

SVM作为监督学习方法的一种，通常用于对数据进行二元分类［6］。其基本思想是利用训练集，在样本空间中找到能够分开不同样本集的划分超平面［7］。但在实际问题中所遇到的样本通常是线性不可分的，对于该问题通常的解决方法为将样本的原始空间映射到更高维的空间中，使样本集在高维空间内实现线性可分［8］。在线性不可分的问题中，找到合适的核函数对样本分类准确性起到决定性的作用［9］。

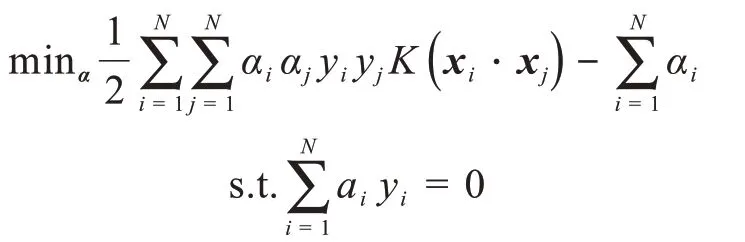
选择α的一个正分量0＜αj＜C，计算

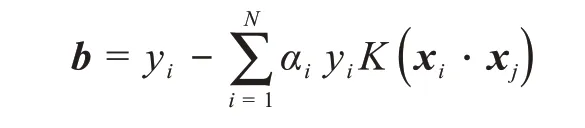
构造决策函数

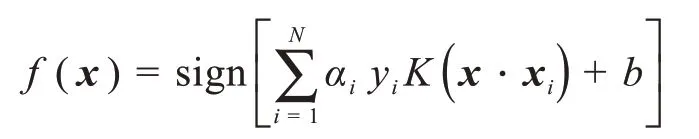
即为支持向量机的决策模型，其中sign（·）为符号函数。

使用Python的scikit-learn库来实现上述支持向量机算法，并选取了多种不同的核函数，分别进行训练和10折交叉验证，并根据交叉验证的结果，比较他们的交叉验证准确率，最终选择线性核函数。而对于惩罚系数，也使用类似的方法进行分别训练和验证，选择C=1。最终使用择优后的各种参数训练得到的模型对测试数据进行预测，核函数和惩罚系数的交叉验证结果如表3和表4所示，所选择的最佳参数为：核函数kernel=linear，惩罚系数C=1。

表3 核函数选择结果Τab.3 Selection results of Kernel function

表4 惩罚系数选择结果Τab.4 Selection results of penalty coefficient

针对P300信号的分类问题，利用来源于5位被试者的相同实验条件的样本，采用多样本融合思想，分别用5位被试者的实验样本训练支持向量机模型，对不同样本的分类结果进行融合，融合规则［11］为

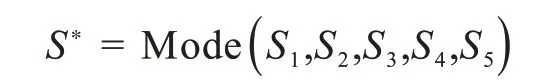
其中Mode（·）为取众数操作，S1至S5为5位被试者样本所分别训练的支持向量机模型给出的分类结果，即采用出现次数最多的分类结果作为该实验最终的分类结果。

2 结果与讨论

使用前述的支持向量机模型对5位被试者（表示为S1-S5）的检测数据进行预测，获得其行列刺激对应数据样本的分类标签，然后定位出待测字符，总共得出对char13-char22共10个待测字符的结果。

与训练数据保持一致，对单次试验中不同轮次内相同行/列的标识符对应的数据进行叠加求平均的处理，同时为了讨论尽可能使用较少轮次的效果［12］，对5轮试验的数据进行逐次剔除最后一轮的操作，分别使用5、4、3、2轮数据，将5个被试者得出的行列预测结果分别利用多样本融合得到最终的行列结果从而得出预测字符，如图4所示，对比了对每个被试者样本单独使用支持向量机分类和采用多样本融合的支持向量机分类准确率指标。

图4 使用不同轮次测试数据的分类准确率对比Fig.4 Comparison of classification accuracy using different rounds of test data

准确率以行列预测正确率计算［13］。对于每一个字符的12条数据，都有2条为正类，其他10条为负类，支持向量机模型给出每条数据的正负类预测结果，从而计算准确率，但由于数据正负类数量严重不平衡，因此对正负类数据的准确率进行了加权平衡［14］：

其中t为真正类（true positive）数目，表示模型对真实类别为正类的样本识别正确。f为假负类（false negative）数目，表示模型把真实类别是正类的样本错误的识别成为负类。n为真负类（true negative）数目，表示模型对真实类别为负类的样本识别正确。p为假正类（false positive）数目，表示模型把真实类别是负类的样本错误的识别成为正类［15］。由于正负类比例为1∶5因此式中取α=0.8,β=0.2。

从图4中可以发现，本研究所提出的多样本融合的支持向量机分类模型相比单一的支持向量机算法在准确率上有了显著的提高。另外在逐步减少检测数据轮次的过程中，模型预测结果逐渐变差。针对本研究所涉及到的数据，在保证模型预测效果的前提下，为了尽可能减少数据量，可以仅使用4轮实验数据来进行分析。

3 结 论

针对P300电位对应字符的预测，本质是二分类问题，在考虑多种分类方法之后，选择了基于线性核函数的支持向量机模型进行P300电位的分类识别。本文提出的模型优点在于对数据做了充分的预处理，使用过采样解决了P300电位分类识别中的类别不平衡导致模型过拟合的问题，并结合了多名受试者的预测结果进行多样本融合来获得最终一致性结果，其预测字符的准确率很高，并且有较高的扩展性和通用性，应用前景广泛。