离心泵叶轮湿模态及其影响参数分析

朱启培，李育房，王彦伟

武汉工程大学机电工程学院，湖北 武汉430205

流体介质中离心泵叶轮固有频率和振型与空气中相比均存在差别［1］，对叶轮进行流固耦合下的湿模态分析、获取叶轮真实工作环境下的固有频率和振型，对于后续精确进行叶轮动力学分析具有重要参考价值。增大叶轮前后盖板曲率半径作为一种改变叶轮固有频率的方法，对离心泵水力状况影响小，可为离心泵叶轮结构进行优化设计以及模态分析提供参考。目前国内外对水泵以及其它流体机械湿模态研究较为广泛，例如，高海司等［2］对蜗壳式混流泵进行流固耦合下的湿模态的研究，分析了预应力存在情况和前、后盖板厚度对模态的影响，结果表明：预应力作用下叶轮固有频率基本不变，而盖板厚度对叶轮各阶次固有频率影响明显。尹庭赟等［3］针对海水淡化增压泵进行了流固耦合作用下的模态分析，结果表明：叶轮材料属性对干、湿模态下固有频率影响显著，材料的杨氏模量越大，叶轮各阶次固有频率越高。Egusquiza和Rodriguez等［4-5］采取试验及数值分析的方式，对水轮机分别在流体和空气中进行了模态分析，结果表明：流体中的振型与空气中相同；但在水体中，叶轮固有频率会因为水的附加质量效应而降低。张新和陈宇杰等［6-7］基于流体的可压缩性分析了卧式轴流泵叶轮干、湿状态下的模态特性，结果表明相对于空气中，水体中叶轮各阶次固有频率降低且各阶次振型的振动幅值有所减小。

国内外学者对泵的叶轮模态做了大量研究工作，并取得较好成果，但针对离心泵叶轮前、后盖板弧度大小对其固有频率的影响研究极少。本文以Q5H26离心泵叶轮为研究对象，通过数值模拟首先得到叶轮流道压力分布状况，验证了叶轮流道的合理性；进而通过声固耦合算法，对叶轮进行湿模态特性分析；最后以叶轮前、后盖板曲率半径为设计参数对叶轮进行干、湿模态分析，分析结果验证了所选参数的合理性。

1 理论基础

离心泵叶轮动力学方程为：

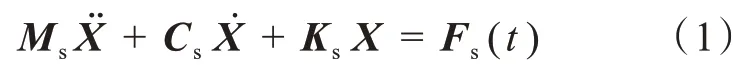
式（1）中，Ms、Cs、Ks分别为系统质量矩阵、阻尼矩阵以及刚度矩阵分别为加速度矢量、速度矢量以及位移矢量；Fs（t）为离心泵所受的预应力，即：流体作用力、自身重力以及自转离心力。

离心泵叶轮在空气中模态分析称为干模态分析，称之为无阻尼模态，因此：Cs=0、Fs（t）=0，式（1）的动力学方程可简化为：

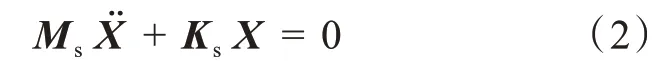
对离心泵叶轮水环境下的模态分析属于湿模态分析，液体对叶轮结构具有耦合作用，考虑液体为静态水域且无黏度均匀的可压缩声学流体，故流体的三维波动方程为：

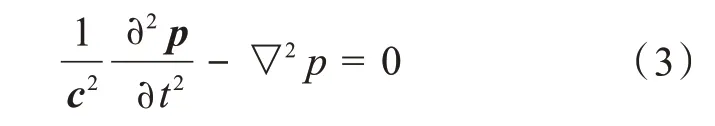
式（3）中，c为声音在流体中的速度，其大小由公式确定；k为流体压缩模量；p为流体压力，ρf为流体的密度。

将式（3）离散化可得流体的动力学方程：

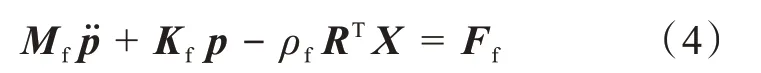
式（4）中，Mf为流体质量矩阵；Kf为流体的刚度矩阵；p为流体压力；R为流体和结构的耦合矩阵；Ff为作用在流体上的外力。

流体介质对叶轮结构所产生的作用可表示为：

式（5）中，n为交界面的法向量；▽p为沿着法线向量的压力梯度；ü为液体质点的速度矢量。对于声学流体所产生的作用，叶轮结构的动力学方程为：

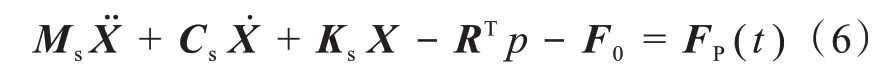
式（6）中，Fp（t）为流-固接触面上的面力向量；F0为施加在叶轮结构上的流体力。

故联立式（4）与式（6），得到叶轮结构流场耦合三维方程：

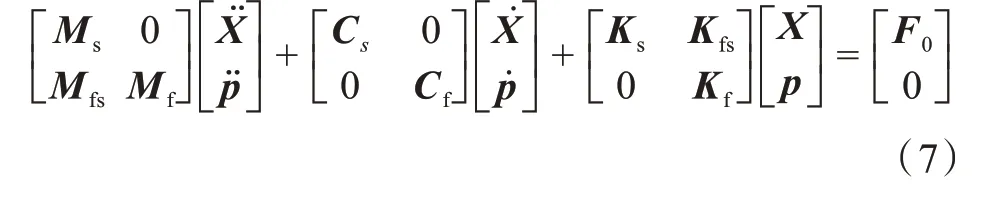
式（7）中，Mfs为等效耦合质量矩阵；Kfs为等效耦合刚度矩阵。

2 模型的建立及边界条件设置

2.1 离心泵模型参数

本文选取型号为Q5H26的高速离心泵进行研究，其叶轮外径D2=62 mm，叶片数Z=6，设计流量Q=5 m3/h，转速n=7 000 r/min，流体密度ρf=1 200 kg/m3，设计扬程Ht=26 m。为了更加真实地描述叶轮所受到的流体作用力，构建离心泵全流道流场模型，利用Solidworks建模软件对离心泵叶轮、蜗壳、进出口延伸段进行三维实体建模［8］，建立实体模型。

2.2 叶轮计算模型及网格无关性检验

所选叶轮材质为结构钢，其主要性能参数：杨氏模量E=200 GPa，密度ρ=7 850 kg/m3，泊松比0.3，屈服强度σs=250 MPa。

利用ANSYS对叶轮结构模型进行4种不同尺寸方案进行网格划分，划分后网格的节点和单元数目如表1所示。

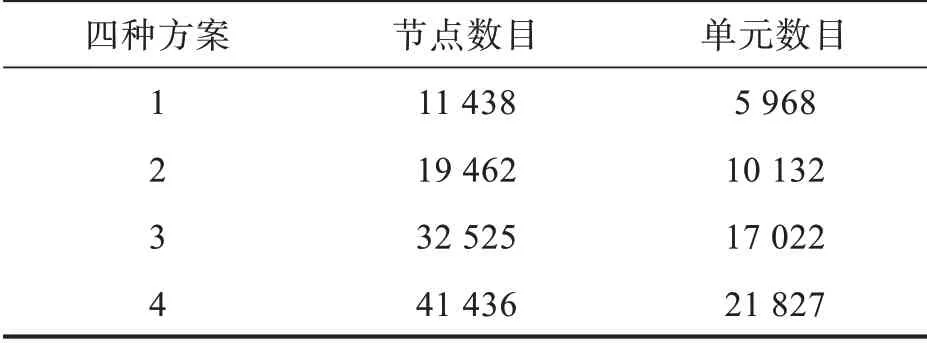
表1 四种不同尺寸的网格节点和单元数目Τab.1 Number of mesh nodes and elements in four different sizes

图1为网格无关性检验结果。由于叶轮整体上为轴对称结构，故第1、2阶固有频率和第4、5阶固有频率相同，他们之间只相差1个相位角，从图1中可以看出单位化的固有频率随着节点数的增加而不断收敛为1，故本文选取方案4进行网格划分。

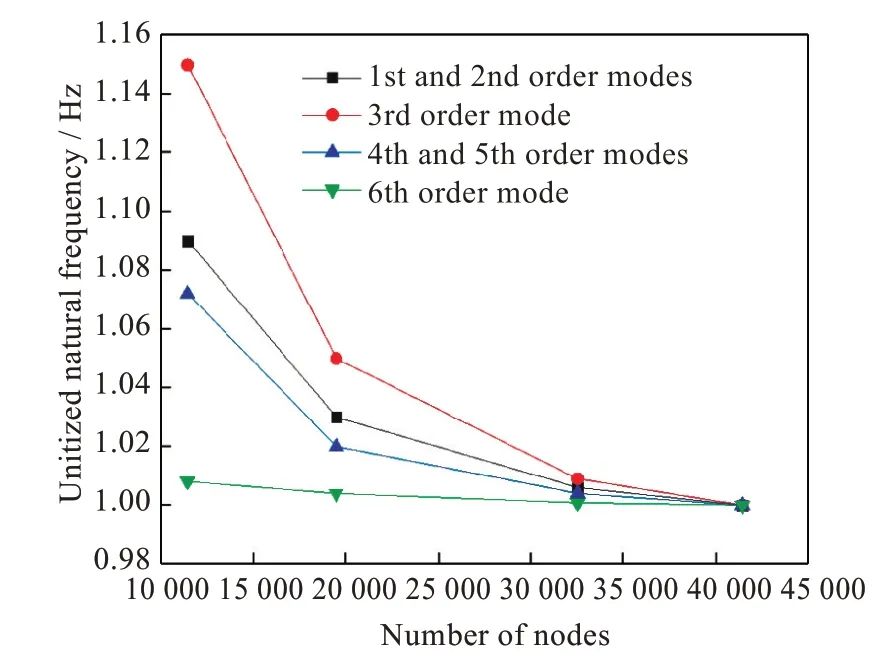
图1 网格无关性检验结果Fig.1 Grid independence test results

2.3 边界条件设置

采用计算流体动力学（computational fluid dynamics，CFD）数值模拟方法，用标准的k-Epsilon湍流模型建立控制方程。泵的外特性数值计算方法采用有限体积法［9-11］。叶轮湿模态分析采用的水体模型由Ansys/Workbench平台中的声学模块Modal Acoustic进行设置，水体模型由长和宽为0.02 m，高为0.01 m的长方体构成，流体密度ρf=1 200 kg/m3，声速c=1 460 m/s；并设置叶轮表面为流固耦合面，同时对叶轮圆孔面施加圆柱约束。

3 结果与讨论

3.1 流场分析结果

在CFX后处理里查看叶轮及其全流道内的静压分布，如图2所示，计算得到离心泵实际扬程Ha=27.684 m，与设计扬程基本吻合，且叶轮叶片整体静压分布均匀，流道设计合理。

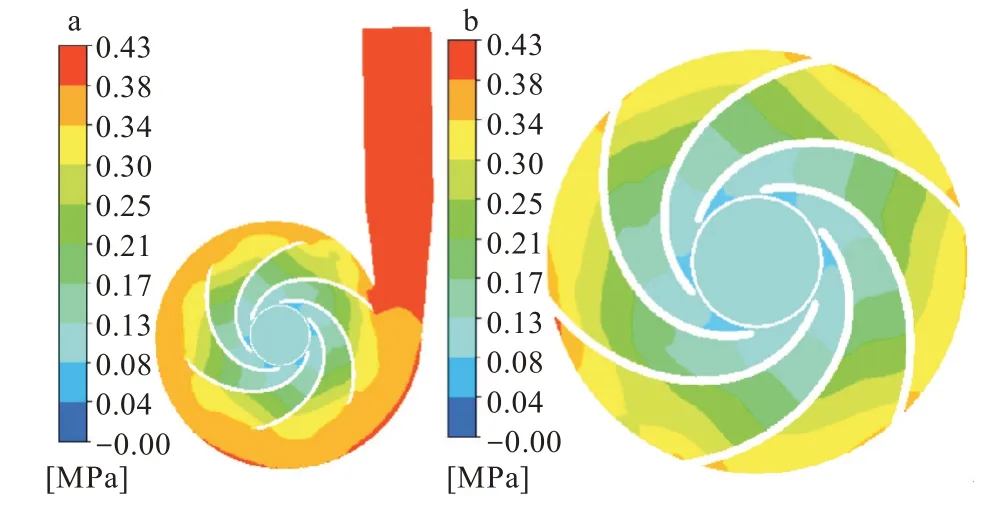
图2 压力分布：（a）全流道静压，（b）叶轮静压Fig.2 Pressure distribution：（a）static pressure of whole flow channel，（b）static pressure of impeller

3.2 干、湿模态结果分析

采取无量纲附加质量系数λ描述水体的附加质量［12-14］，其计算公式如下：

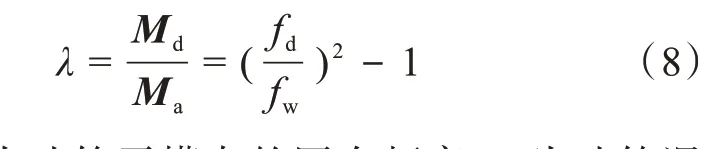
式（8）中，fd为叶轮干模态的固有频率；fw为叶轮湿模态的固有频率；Md为附加质量矩阵。

计算得到叶轮在空气中以及水体下的前4阶固有频率，由表2可以得出，相对于在空气中，水体中叶轮各阶次的固有频率均有所降低，前2阶水体附加质量系数λ=0.74，固有频率下降24%；第3阶水体附加质量系数λ=1.26，固有频率下降较为明显为34%；第4阶附加质量系数λ=0.60，固有频率下降21%。结果表明：相对于干模态，水体的附加质量效应对叶轮固有频率影响较大，由于水体刚度与叶轮结构刚度相比可以忽略，故叶轮固有频率大幅度下降。

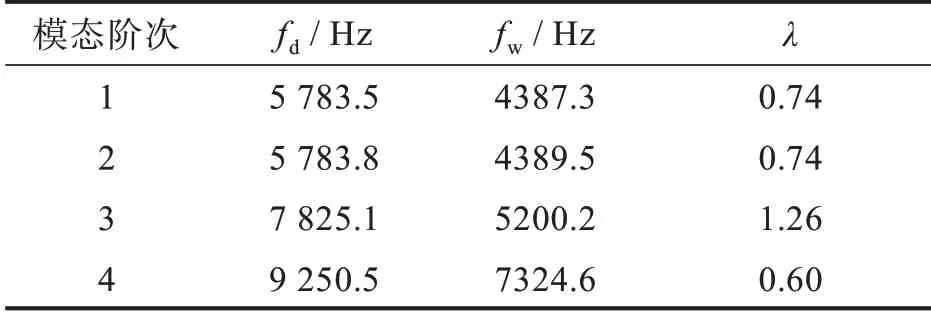
表2 空气中和水体中叶轮前四阶固有频率Τab.2 First four natural frequencies of impeller in air and water

空气中和水体中的前4阶固有频率对应的振型分别如图3和图4所示。第1、2阶振型相同，为叶轮弯曲模态，这是由于叶轮为轴对称模型、振型存在对称性。第3阶为叶轮沿轴向扭转模态。第4阶振型为叶轮前后摆动模态。水体中振型基本与干模态振型保持一致。

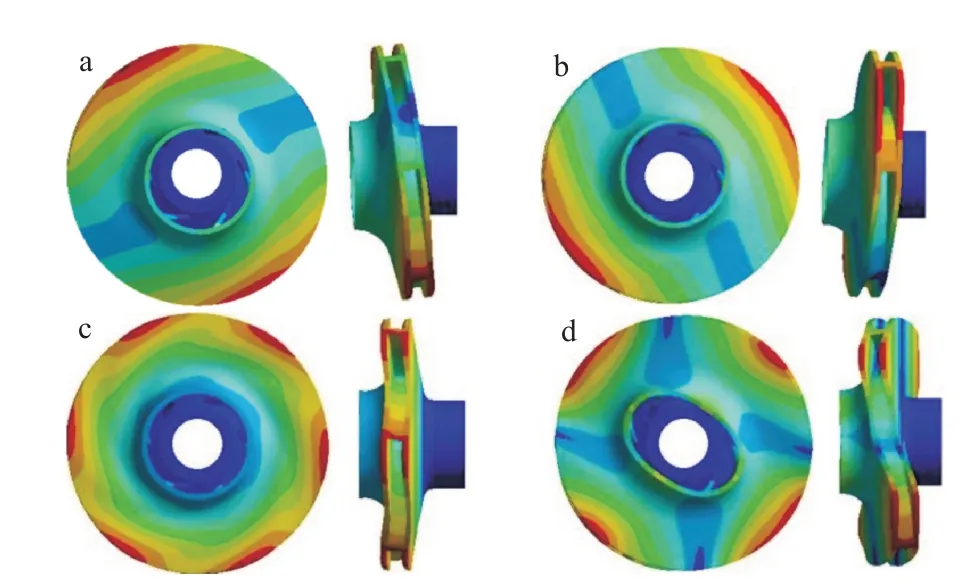
图3 空气中前4阶振型：（a）第1阶模态，（b）第2阶模态，（c）第3阶模态，（d）第4阶模态Fig.3 First four modes in air：（a）first order mode，（b）second order mode，（c）third order mode，（d）fourth order mode

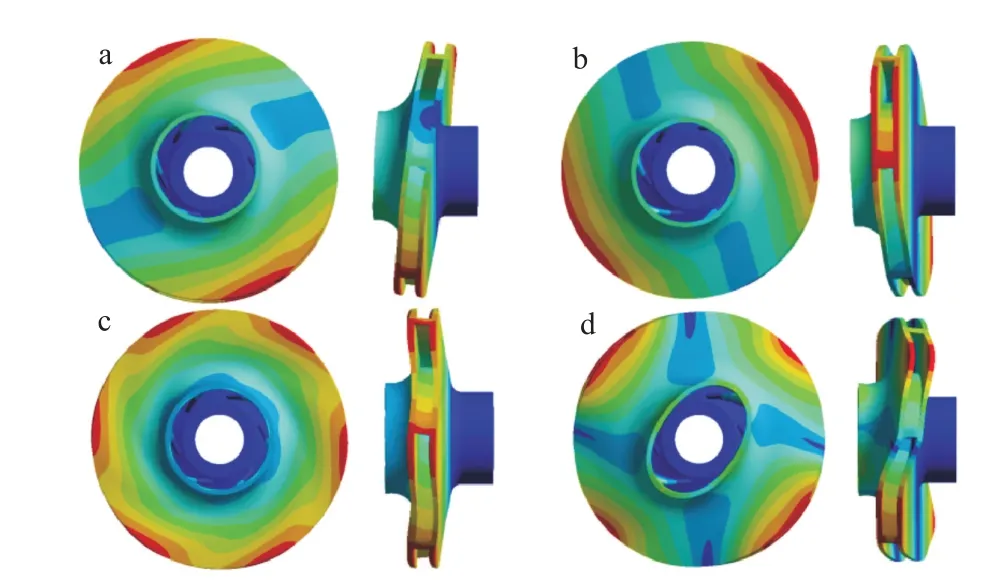
图4 水体中前4阶振型：（a）第1阶模态，（b）第2阶模态，（c）第3阶模态，（d）第4阶模态Fig.4 First four modes in water：（a）first order mode，（b）second order mode，（c）third order mode，（d）fourth order mode

与空气中叶轮模态振型相比，湿模态下的叶轮振动幅值较小，各阶次无量纲附加质量系数λ不同。这是因为叶轮在水体中振动时，对水介质做功，每一阶的振动幅度不同，使得对水介质的所做功的大小也不同，导致叶轮每一阶的固有频率降低系数不同。正是由于叶轮振动对水介质做功，由能量守恒原理可得出叶轮系统的总能量势必减小，使得叶轮在水体中的振动幅度低于在空气中的振动幅度。

4 前后盖板曲率半径对固有频率的影响

改变前、后盖板厚度与叶片厚度会较大程度上改变叶轮质量，改变叶片厚度会对叶轮流道产生较大影响，导致叶轮无法正常工作，且在铸造叶轮时需要重新开模，增加成本与难度［15］。改变叶轮进口直径会直接影响离心泵水力效率，导致水力效率下降；改变叶轮材料属性则会对叶轮抗腐蚀、磨损等产生不利影响，因此选取上述参数为设计参数是不可取的。本文选取叶轮前、后盖板曲率半径为设计参数，它对叶轮质量改变较小，但对叶轮结构刚度却有一定程度的影响。本文研究了不同前、后盖板曲率半径大小对叶轮固有频率的影响，并通过CFX仿真验证了所取设计参数的合理性。

对于前盖板曲率半径，在原设计模型曲率半径rs1=8.3 mm基础上分别取曲率半径为rs2=12.3 mm，rs3=16.3 mm。对于后盖板曲率半径，在原设计模型圆弧半径rh1=18 mm基础上分别取曲率半径为rh2=28 mm，rh3=38 mm。对所取参数进行CFX数值模拟计算，分别得到前后盖板曲率半径与扬程的关系，如图5所示，前盖板曲率半径增大，扬程减小，水力效率下降，后盖板曲率半径增大，扬程增大，提高了水力效率。结果表明：选取前、后盖板曲率为设计参数较为合理，且增大后盖板曲率半径提高了水力效率。

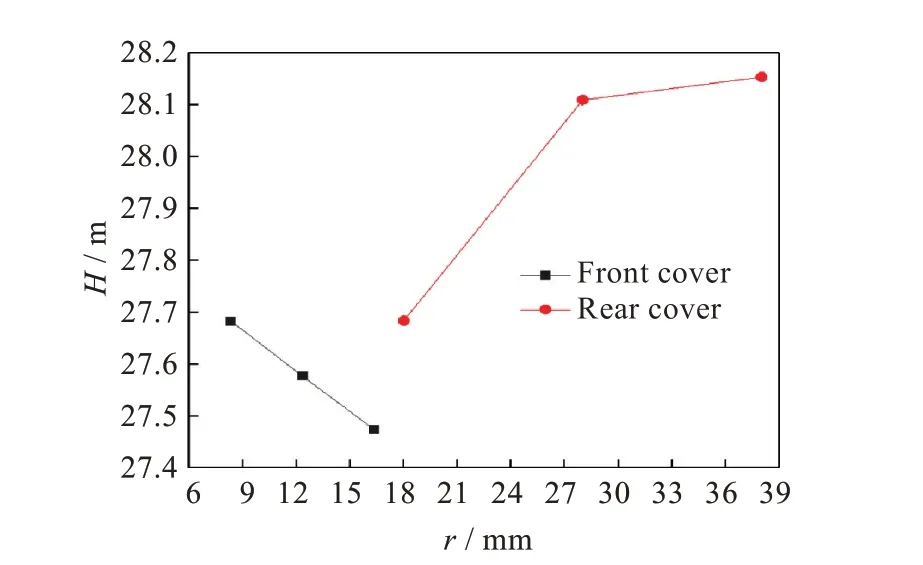
图5 盖板曲率半径对扬程影响曲线Fig.5 Influencecurves of cover plate curvature radius on lift

验证所选参数合理性之后，分别计算得到前后盖板不同曲率半径下的叶轮干、湿模态下的固有频率，计算结果如图6和图7所示，其中N表示叶轮的模态阶次。

由图6（a）和7图（c）可以得出，增大前盖板曲率半径，叶轮第1、2阶干、湿模态的固有频率随着曲率半径增大而减小；而第3、4阶干、湿模态的固有频率随着曲率半径增大而增大，但增大前盖板曲率半径减小了水力效率，故对叶轮结构优化设计以及模态分析时，在保证水力效率下可适当增大前盖板曲率半径。

由图6（b）和图7（b）可以看出，增大后盖板曲率半径增大，叶轮干、湿模态下各阶次固有频率增大，共振频率增大，且干模态下固有频率增幅较湿模态下固有频率增幅大，这是由于湿模态下水体对叶轮所产生的附加质量大，产生的阻尼减弱了叶轮的振动，且增大后盖板曲率半径提高了水力效率，故在对叶轮进行结构优化设计以及需要提高叶轮固有频率时，可增大叶轮后盖板曲率半径。

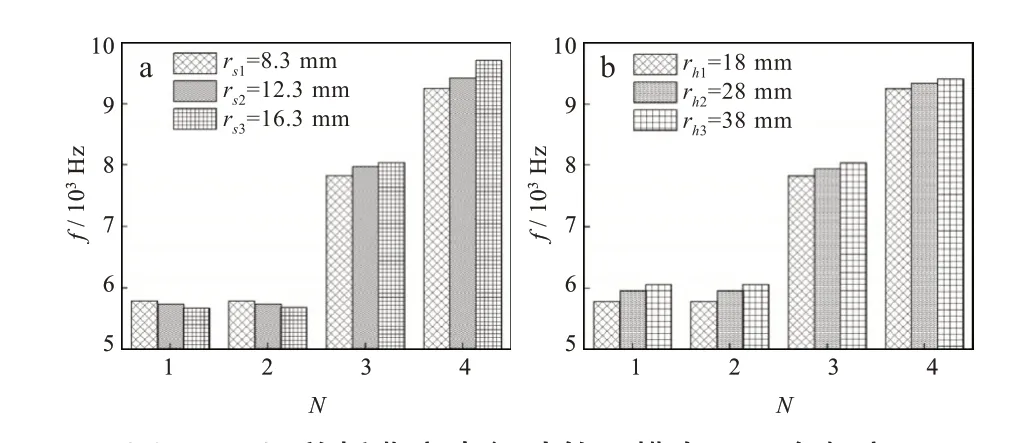
图6 不同盖板曲率半径叶轮干模态下固有频率：（a）前盖板，（b）后盖板Fig.6 Natural frequencies of impeller with different cover curvature radiiin dry mode：（a）front cover，（b）rear cover

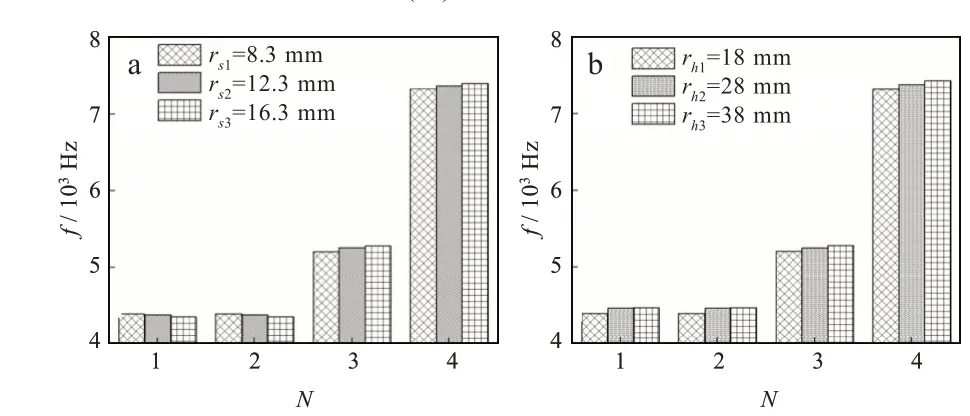
图7 不同盖板曲率半径叶轮湿模态下固有频率：（a）前盖板，（b）后盖板Fig.7 Natural frequencies of impeller with different cover curvature radii in wet mode：（a）front cover，（b）rear cover

5 结 论

通过对比分析离心泵叶轮干、湿模态变化规律以及叶轮前、后盖板曲率半径大小对其干、湿模态的影响，得出结论如下：

1）在流体介质环境下，离心泵叶轮的固有频率相对于空气中的固有频率有所下降，附加质量系数在0.60至1.26之间，干、湿模态下对应的各阶次振型相同且各阶次振型幅值有较为明显的减弱。

2）增大叶轮前盖板曲率半径，流道内压力分布变化合理，扬程减小，水力效率减小；叶轮干、湿模态下前2阶固有频率减小，第3、4阶固有频率增大。

3）增大叶轮后盖板曲率半径，流道内压力变化合理且扬程增大，水力效率最大可提高2%；叶轮干、湿模态下前4阶固有频率增大。