预制拼装钢管混凝土柱偏压性能有限元分析

刘 莉，赵延吉，杨 阳，张 婷

(1.沈阳建筑大学土木工程学院，辽宁 沈阳 110168；2.同圆设计集团股份有限公司，山东 济南 250000)

随着装配式建筑的不断推广，建筑中各类构件的生产正在逐渐走向工业化。为满足施工生产需要，钢管混凝土柱通常被分为若干个节段进行预制，将节段运送到施工现场后进行拼装，这样可以减少现浇混凝土工序，降低对环境的污染，缩短工期。研究预制钢管混凝土柱的节段拼装具有较好的工程意义。

节段拼装钢管混凝土柱主要应用于桥梁工程。国内外学者对预制节段拼装桥墩进行了许多研究[1-5]。何通[6]采用纤维模型法，研究了预制节段拼装混凝土桥墩的抗震性能。布占宇等[7]研究了整体现浇桥墩与预制拼装桥墩抗震性能的差异。张强[8]提出后张预应力节段预制拼装钢管混凝土和高强螺栓连接钢管混凝土桥墩两种构造，并对其进行拟静力对比分析。孔兰兰[9]针对节段拼装钢管混凝土桥墩抗震性能及其基于位移的抗震设计方法进行了研究。翟帅帅[10]提出了两种内套管连接钢管混凝土柱拼接方式，并对螺栓连接钢管混凝土柱的轴压力学性能进行了研究。余琼等[11]针对新型套筒灌浆搭接连接的预制柱进行了抗震性能研究。OuYuchen等[12]通过试验研究了耗能钢筋对节段拼装桥墩自复位性能的影响。C.S.Shim等[13]针对预应力筋连接的节段拼装桥墩进行抗震性能研究。目前，针对全预制节段拼装柱的研究较少，基于此，笔者提出一种新型预制拼装钢管混凝土柱，并利用ABAQUS有限元软件分析其偏压受力性能，研究表明预制连接件内套管长度、内套管壁厚对该柱极限承载力影响不大，长细比、含钢率、偏心距对该柱受力性能影响较大。

1 内套管连接钢管混凝土柱有限元模型

1.1 材料本构关系

笔者选取韩林海[14]提出的钢管混凝土构件中核心混凝土本构关系模型，在ABAQUS软件的材料库中，选取混凝土的塑性损伤模型来进行分析。采用应力-断裂能(GFI)来定义混凝土受拉性能。钢管采用五阶段二次塑流模型[15-16]。

1.2 单元类型选取

内套管连接的钢管混凝土柱模型主要由上下两端端板、钢管、内套管、核心混凝土、螺栓五部分组成。在ABAQUS软件中，端板、钢管、内套管、核心混凝土、螺栓均采用8节点减缩积分格式的三维实体单元(C3D8R)。

1.3 模型接触与边界条件

内套管连接的钢管混凝土柱模型在承受外荷载时，核心混凝土、内套管、钢管、端板、螺栓之间会产生相互作用。内套管与核心混凝土采用绑定接触(Tie)进行约束；钢管与混凝土之间的界面关系由两个方向决定，法线方向采用硬接触(Hard contact)，切线方向采用罚函数(Penalty)，摩擦系数为0.3；滑移模式采用有限滑移(Finite sliding)；钢管与端板之间采用绑定接触；端板与核心混凝土之间采用硬接触。

约束柱上表面x、y方向位移以及沿x、y、z轴的转角，将柱下表面设置为完全固定。

1.4 模型有效性验证

根据文献[10]中编号为LZ-1、LZ-2、LZ-3、LZ-4试件，在ABAQUS中建立相对应有限元模型，模型编号与试件编号相同。以试件LZ-1为例，荷载-位移曲线(纵向)对比结果见图1。

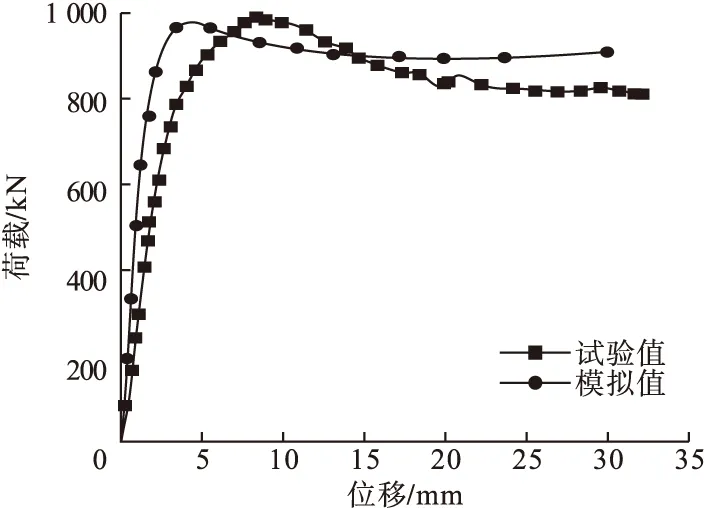
图1 试件LZ-1荷载-位移曲线对比Fig.1 Comparison of load-displacement curves

从图1中可以看出，荷载-位移曲线与试验结果吻合较好，验证了有限元模型的有效性。由于有限元计算是在相对理想状态下进行的，排除了试验过程中的各种不利因素，所以有限元计算出的数值略大于试验数值。

2 预制拼装钢管混凝土柱

2.1 预制拼装钢管混凝土柱构造

笔者提出的预制拼装钢管混凝土柱构造如图2所示。

图2 预制拼装钢管混凝土柱节段构造Fig.2 Segment structure of precast assembled concrete filled steel tube column

图中1为圆钢管，2为混凝土，3为环形挡片，4为圆钢片，5为圆形钢片环，6为螺栓孔，7为加劲肋板。与上述试验中内套管连接钢管混凝土柱相比，各组成部分完全预制，没有现场浇筑过程。

2.2 轴压下预制拼装钢管混凝土柱破坏分析

预制拼装钢管混凝土柱模型尺寸与文献[10]中试验试件LZ-1、LZ-2、LZ-3、LZ-4相同，编号分别为LS-1、LS-2、LS-3、LS-4。模型计算设有两个分析步：①对螺栓施加125 kN的螺栓荷载；②对模型施加与内套管连接钢管混凝土柱相同的荷载。预制上节段中的核心混凝土、预制连接件中的核心混凝土、预制下节段中的核心混凝土的界面接触关系采用罚函数。

将LS-1、LS-2、LS-3、LS-4承载力与内套管连接钢管混凝土柱的极限承载力相比较，结果见表1。以LS-1、LS-2为例，荷载-位移曲线(纵向)见图3。从图中可以看出，加载初期，预制节段外钢管与核心混凝土均处于弹性工作阶段，荷载-位移曲线呈线性增长。随着荷载增加，荷载-位移曲线由线性增长转为非线性增长，预制节段外钢管逐渐达到屈服强度，此时外荷载再继续增加，受压钢管逐渐产生塑性变形，受压混凝土会产生微小裂缝，直到模型达到极限承载力。继续施加荷载，混凝土内部微小裂缝快速发展，荷载-位移曲线呈下降趋势，随后模型承载力下降至趋于平缓，由于预制节段外钢管和预制连接件钢管的双重套箍作用，荷载-位移曲线出现小幅度回升现象。从表1可以看出，试验值与模拟值的比值为1.018、1.006、0.999、1.005，误差较小。从图3可以看出，荷载-位移曲线走势基本吻合，说明所建立的预制拼装钢管混凝土柱模型在轴压荷载下，其受力过程同内套管连接钢管混凝土柱基本相同。由此表明，在轴压荷载下，预制拼装钢管混凝土柱可以替换同条件下内套管连接的钢管混凝土柱，同时在工程中构件全装配、减少工人工作量、减少施工现场湿作业量、缩短工期、节约成本等优点。

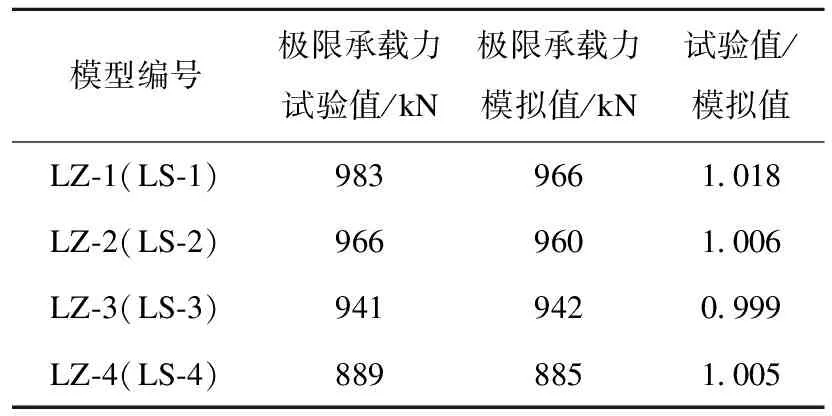
表1 极限承载力有限元结果与试验结果对比Table 1 Comparison of ultimate bearing capacity finite element results and test results

图3 荷载-位移曲线Fig.3 Load-displacement curves

2.3 偏压下预制拼装钢管混凝土柱破坏分析

以模型LS-2为例，偏压下预制拼装钢管混凝土柱最终应变云图如图4所示。可以看出，预制拼装钢管混凝土柱在偏压荷载作用下产生了较大的侧向变形。

图4 最终应变云图Fig.4 Final strain contour plot

图5为模型截面宽度变化量，初始截面宽度为140 mm。从图5可知，在整个偏压加载过程中，模型的截面宽度始终在变化，加载最终阶段，在高度为100 mm和600 mm左右处，模型的截面宽度产生较大的变化量，即模型在偏压加载过程中会发生鼓曲膨胀现象，并在高度为100 mm和600 mm左右处时，鼓曲膨胀最大，且在100 mm的位置处最大，模型截面宽度增大了约0.9 mm。

图5 模型截面宽度变化曲线Fig.5 Model section width change curves

3 偏压下预制拼装钢管混凝土柱参数分析

笔者建立15个预制拼装钢管混凝土柱模型，分析预制连接件内套管长度、内套管壁厚以及长细比、含钢率、偏心距对预制拼装钢管混凝土柱受力性能的影响，模型参数见表2。

表2 偏压模型参数Table 2 Eccentric compression model parameters

3.1 预制连接件内套管长度

不同预制连接件内套管长度下对应的模型极限承载力见表3。

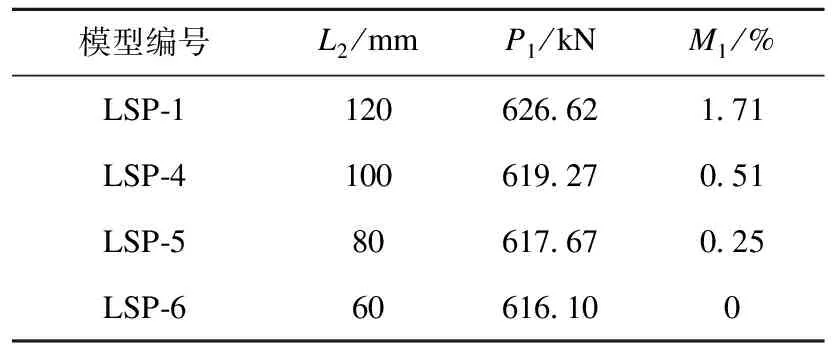
表3 偏压下内套管长度对模型极限承载力的影响Table 3 The influence of the inner sleeve length on the ultimate bearing capacity of the model under eccentric compression

由表3可以看出，预制连接件的内套管长度对模型极限承载力的影响并不大，内套管长度从60 mm增加到120 mm时，模型的极限承载力仅仅增加了1.71%，但是增加的幅度逐渐增大。预制连接件的内套管越长，模型预制连接件区域就越大，对预制连接件核心混凝土约束越强，导致模型的承载能力略有增大。

3.2 预制连接件内套管壁厚

不同预制连接件内套管壁厚对应的模型极限承载力见表4。从表可知，内套管壁厚从1.75 mm增加到4.75 mm时，模型的极限承载力仅仅增加了1.54%，即内套管壁厚增大，模型的极限承载力幅度提高较小。

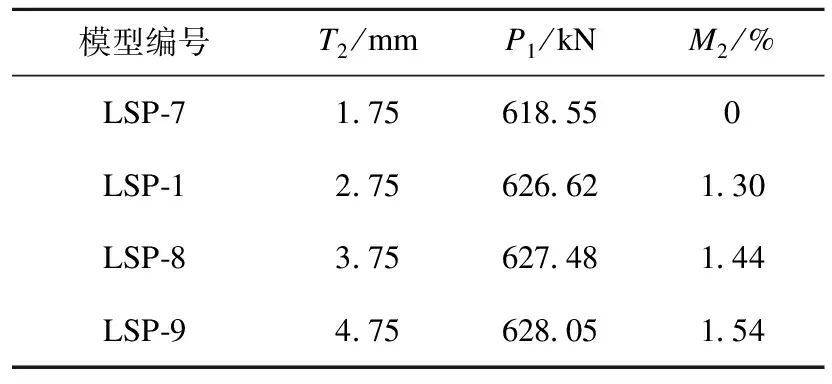
表4 偏压下内套管壁厚对模型极限承载力的影响Table 4 The influence ofthe inner sleeve thickness on the ultimate bearing capacity of the model under eccentric compression

3.3 长细比

以模型LSP-2、LSP-10、LSP-11、LSP-12为例，绘制预制拼装钢管混凝土柱在不同长细比下的荷载-跨中挠度曲线如图6所示，初始刚度如图7所示。

图6 不同长细比下的荷载-跨中挠度曲线Fig.6 Load-midspan deflection curves at different slenderness ratios

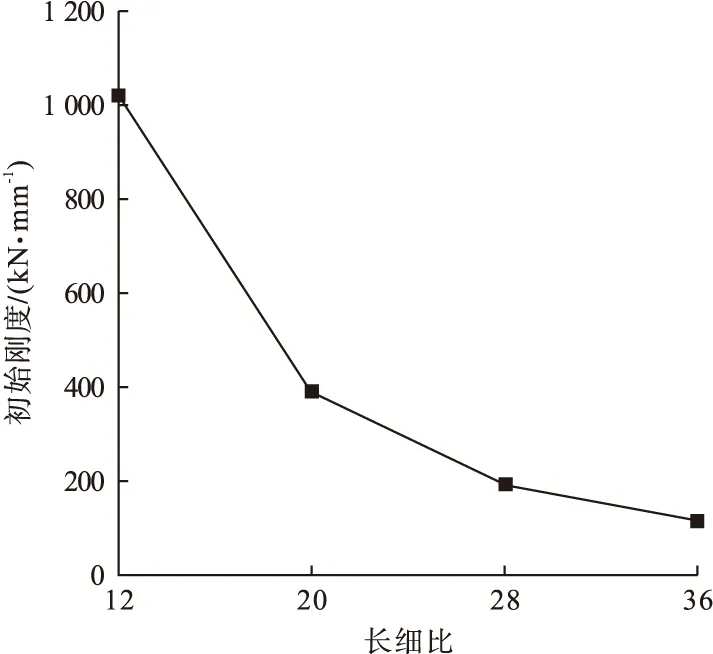
图7 不同长细比下的初始刚度Fig.7 Initial stiffness at different slenderness ratios

从图6可以看出，当长细比为12时，荷载-跨中挠度曲线始终呈上升趋势，当模型达到屈服强度后，模型始终处于强化阶段，承担的外荷载始终增大。当长细比为20及以上时，模型达到屈服强度后，荷载变化较小。这是由于长细比越小，模型的预制连接件区域面积所占整体的比例就越大，抗横向变形能力就越强。长细比为12、20、28、36时，预制柱极限荷载分别为510.37 kN、460.34 kN、421.17 kN、408.00 kN，此时跨中挠度分别为2.42 mm、8.46 mm、16.31 mm、22.63 mm。以长细比12为参考值，长细比增加66.67%、133.33%、200%，极限荷载值分别降低9.80%、17.48%、20.06%，此时跨中挠度值分别增加249.59%、573.97%、835.12%，对应的初始刚度减小61.57%、81.00%、88.56%。可见，预制拼装钢管混凝土柱长细比越大，其极限承载能力越低，跨中挠度值越大，初始刚度越低。

3.4 含钢率

以模型LSP-2、LSP-13、LSP-14、LSP-15为例，绘制预制拼装钢管混凝土柱在不同含钢率下的荷载-跨中挠度曲线如图8所示，初始刚度如图9所示。

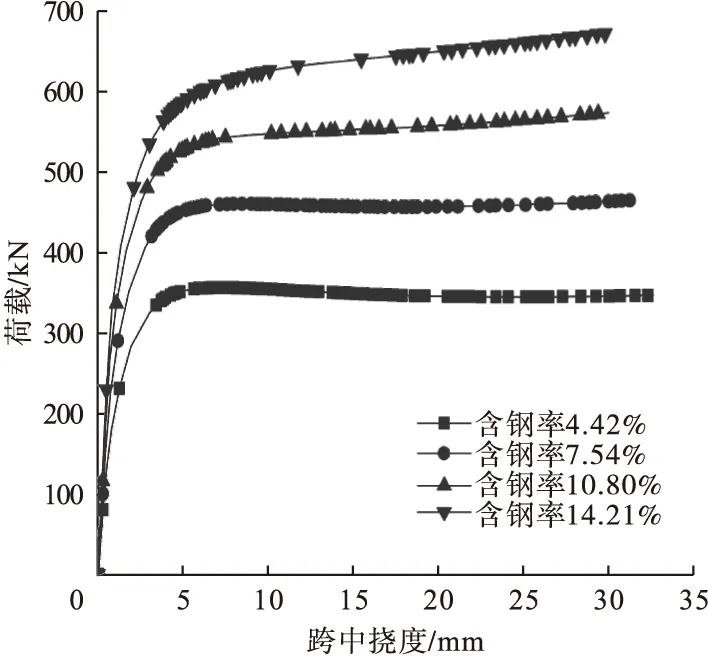
图8 不同含钢率下的荷载-跨中挠度曲线Fig.8 Load-midspan deflection curves at different steel ratios

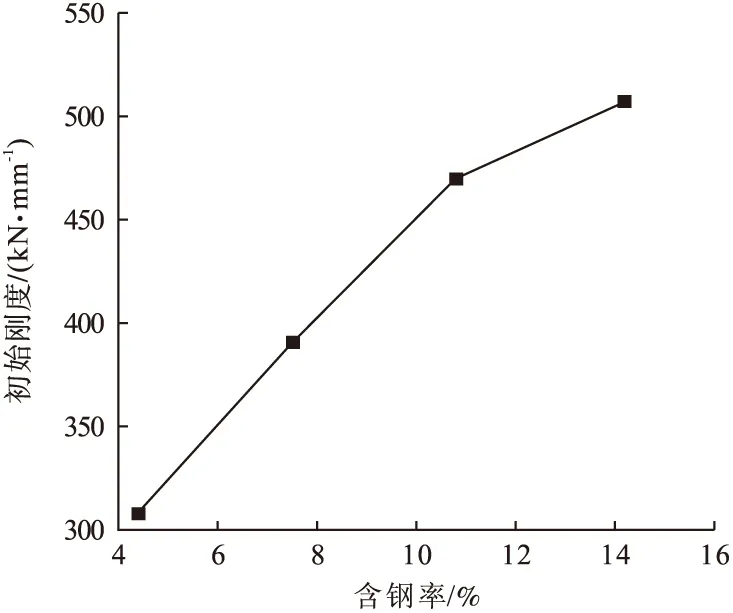
图9 不同含钢率下的初始刚度Fig.9 Initial stiffness at different steel ratios

从图8可以看出，当含钢率为10.80%、14.21%时，荷载-跨中挠度曲线始终呈上升趋势，当模型达到屈服强度后，模型始终处于强化阶段，承担的外荷载始终增大。这是由于含钢率越大，即钢管越厚，套箍系数越大，抗横向变形能力越强。当含钢率为4.42%、7.54%时，模型达到屈服强度后，极限承载力变化较小。含钢率为4.42%、7.54%、10.80%、14.21%时，预制柱的极限荷载分别为356.24 kN、460.34 kN、548.47 kN、629.11 kN。以含钢率4.42%为参考值，含钢率增加70.59%、144.34%、221.49%，极限荷载值增加29.22%、53.96%、76.60%，初始刚度增大27.12%、52.65%、64.77%。可见，预制拼装钢管混凝土柱含钢率越大，模型极限承载力、初始刚度越大。

3.5 偏心距

以模型编号LSP-1、LSP-2、LSP-3为例，绘制预制拼装钢管混凝土柱在不同偏心距下的荷载-跨中挠度曲线如图10所示，初始刚度如图11所示。偏心距为20 mm、40 mm、60 mm时，预制柱的极限荷载分别为626.62 kN、460.34 kN、321.19 kN。以偏心距20 mm为参考值，即偏心距增加100%，200%，极限荷载值减少26.54%，48.74%，初始刚度减小41.90%、62.82%，可见，偏心距越大，模型的极限承载力、初始刚度越低。

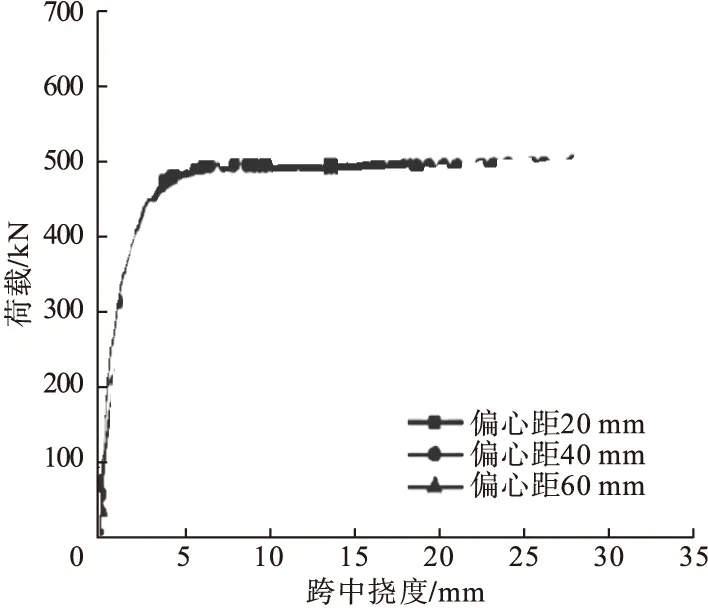
图10 不同偏心距下的荷载-跨中挠度曲线Fig.10 Load-midspan deflection curves at different eccentricity

图11 不同偏心距下的初始刚度Fig.11 Initial stiffness at different eccentricity

不同偏心距下的荷载-纵向应变曲线如图12所示。从图中可以看出，不同偏心距下的模型在加载初期，荷载-纵向应变曲线均呈线性增长，同时在模型的全截面上始终存在受压区和受拉区。当偏心距为20 mm、40 mm、60 mm时，压应变分别约为拉应变的6倍、4倍、2倍。可见，随着偏心距的增大，模型截面上的压应变与拉应变的比值降低。模型在达到极限承载力之前，受压区的应变增长速率低于受拉区。

图12 不同偏心距下的荷载-纵向应变曲线Fig.12 Load-longitudinal strain curves under different eccentricity

4 结 论

(1)预制连接件内套管长度、内套管壁厚对预制拼装钢管混凝土柱承载力影响较小。

(2)预制拼装钢管混凝土柱长细比越大，极限承载力越低，跨中挠度值越大，初始刚度越低；含钢率增大，极限承载力提高，初始刚度增大；偏心距增大，极限承载力降低，初始刚度降低，截面上的压应变与拉应变的比值会降低。