双节点板式K形外置钢支撑-方钢管柱连接节点力学性能的有限元分析

李帼昌，聂金乾，杨志坚，邱增美

(沈阳建筑大学土木工程学院，辽宁 沈阳 110168)

钢材具有强度高、塑性韧性好等优点，被广泛应用于多、高层建筑和工业建筑领域[1-2]。与普通钢框架结构体系相比，钢框架-支撑结构体系作为一种双重抗侧力体系，其抗侧刚度更大、抗震性能更好。但由于支撑的存在，经常会影响钢框架-支撑结构体系房屋建筑立面设计、门窗布置等[3]。为了避免支撑对门窗洞口布置的影响，李帼昌等[4]提出了一种新型钢框架支撑结构形式，即外置支撑-钢框架结构体系。

节点的性能对钢框架-支撑结构体系的受力性能有重要影响，研究发现，在地震作用下，连接节点的破坏可能会导致框架结构倒塌[5]。因此节点的抗震性能和破坏模式越来越受到各国学者重视，节点的构造与计算理论逐渐丰富起来[6]。J.Vesecky[7]通过试验研究了几何尺寸和螺栓数量对节点板连接节点极限承载力的影响；Q.Sun[8]通过试验与有限元结合的方法对KK型管板节点进行研究，并建立了KK型管板节点极限承载力的计算公式；谢思昱等[9]提出了两种提高带支撑节点板钢框架梁柱节点的力学性能的方法；K.A.Skalomenos等[10]通过试验得出支撑节点板连接节点的抗震性能与节点板的断裂能力密切相关；王孟鸿等[11]通过有限元分析的方法研究了节点板厚度、加载方向等参数对K形管板节点受力性能的影响。

传统的钢结构节点多为焊接节点，因其需要进行现场焊接，大大降低了施工效率，同时现场焊接受到环境和作业条件的影响，焊缝的质量难以保证。基于此，笔者提出一种应用于外置支撑钢框架结构体系新型装配式连接节点，即双节点板式K形外置钢支撑-方钢管柱连接节点。通过改变不同的参数分析其对新型节点的承载能力和延性等的影响。研究表明，新型节点的抗震性能良好，可以用于外置支撑-钢框架结构体系。

1 双节点板方钢管柱-K形钢支撑连接节点设计

双节点板连接节点结构示意图如图1(a)所示，包括方钢管柱、钢板、节点板、钢支撑、对拉螺栓以及高强螺栓。在新型节点中，方钢管柱与钢板对应位置开设螺栓孔，通过对拉螺栓连接，节点板与钢支撑通过高强螺栓连接，节点板与钢板采用焊接连接，各构件参数见图1(b)。

图1 双节点板节点Fig.1 The double gusset plate joint

(2)

(3)

(4)

从计算结果可知，方钢管柱的局部稳定和长细比满足要求；支撑的局部稳定满足要求。方钢管柱、钢板及钢支撑上螺栓孔间距满足《钢结构设计标准》(GB 50017—2017)[13]规定的尺寸要求。

2 新型节点有限元模型的建立

2.1 本构关系的选取

钢材的应力-应变关系采用双线性强化模型[14]。钢支撑采用Q235钢材，其他构件采用Q355钢材，螺栓使用10.9级M20高强螺栓，弹性模量取2.06×105MPa，泊松比取0.3。

2.2 有限元模型的建立

利用ABAQUS有限元分析软件，对双节点板方钢管柱-K形钢支撑连接节点建立三维实体模型，所有部件单元类型均采用C3D8R。螺栓施加预紧力，螺栓孔径为22 mm，根据《钢结构设计标准》(GB 50017—2017)要求施加预紧力155 kN。节点模型网格划分情况如图2所示，节点域网格密度适当加大。

图2 模型及部件网格划分Fig.2 Mesh generation of models and components

节点板与钢板之间设置为“绑定”接触；对拉螺栓和高强螺栓杆与各孔壁之间设置垂直于接触面的“硬”接触。由于钢支撑翼缘与节点板之间、螺帽与钢板之间、钢板与方钢管柱之间存在微小滑动，设置垂直于接触面的“硬”接触和平行于接触面的“摩擦”接触，摩擦因子取0.35[15]。模型的边界条件：柱顶U1=U2=0，UR2=UR3=0；柱底U1=U2=U3=0，UR2=UR3=0，沿支撑轴线方向施加位移荷载。

选取对拉螺栓直径、节点板厚度、方钢管柱壁厚及高强螺栓直径为变化参数，共建立4组13个模型。模型主要参数见表1，表中D1表示对拉螺栓直径，Bb表示节点板厚度，Bz表示方钢管柱壁厚，D2表示高强螺栓直径。

表1 模型参数Table 1 Model parameters

2.3 有限元模型的验证

笔者选取文献[16]中的模型S1验证模型的准确性。有限元结果与试验结果对比如图3所示。从图中可以看出，有限元模拟与试验破坏模态相同，均为钢梁与端板连接处产生了较大的变形；模拟所得的极限承载力较试验值仅高5.4%，误差较小，说明文中模型建立方法和所使用的本构关系适用性较好，可以进行后续模拟分析。

图3 试验与有限元结果对比Fig.3 Comparison of test and finite element results

3 单调荷载作用下有限元分析

3.1 典型模型分析

文中各模型均在模型DB-3的基础上进行参数变化，故选取模型DB-3作为典型模型进行分析。取两个钢支撑端部为加载点，上侧受压、下侧受拉。构件DB-3加载点的荷载-位移曲线如图4所示。

图4 加载点荷载-位移曲线Fig.4 Force-displacement curves of loading points

从图4可以看出，节点受压、受拉两侧加载点的荷载-位移曲线走势大致相同，可定义三个特征点，并将荷载-位移曲线分为以下三个阶段：弹性段、弹塑性段、平缓段。

弹性段(OA段：P≤46.1%Pu；OD段：P≤39.6%Pu，其中Pu为极限荷载)。此阶段节点各构件处于弹性状态，各构件的应力较小，加载点的荷载与位移基本呈线性关系。

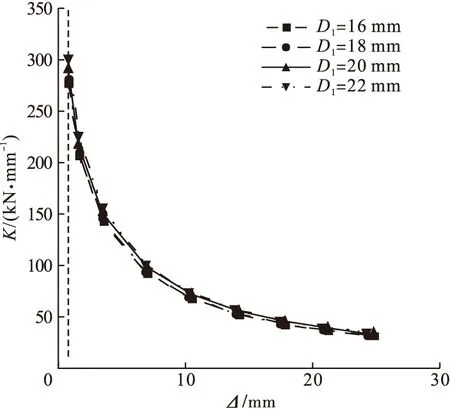
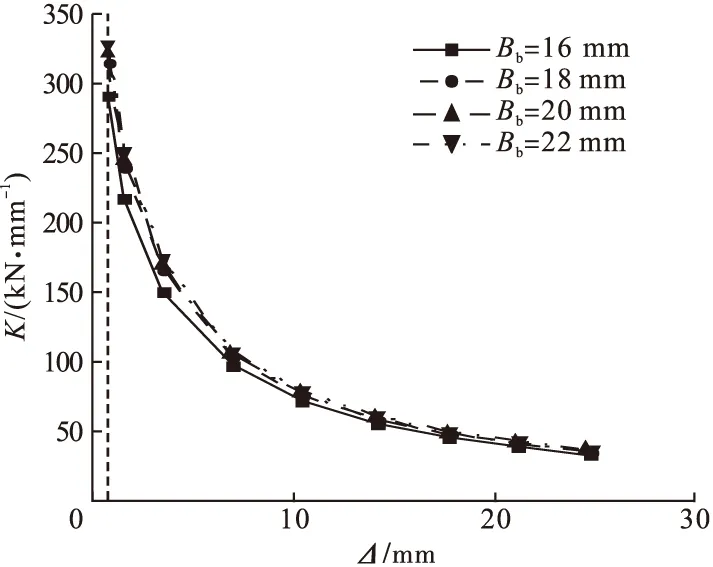
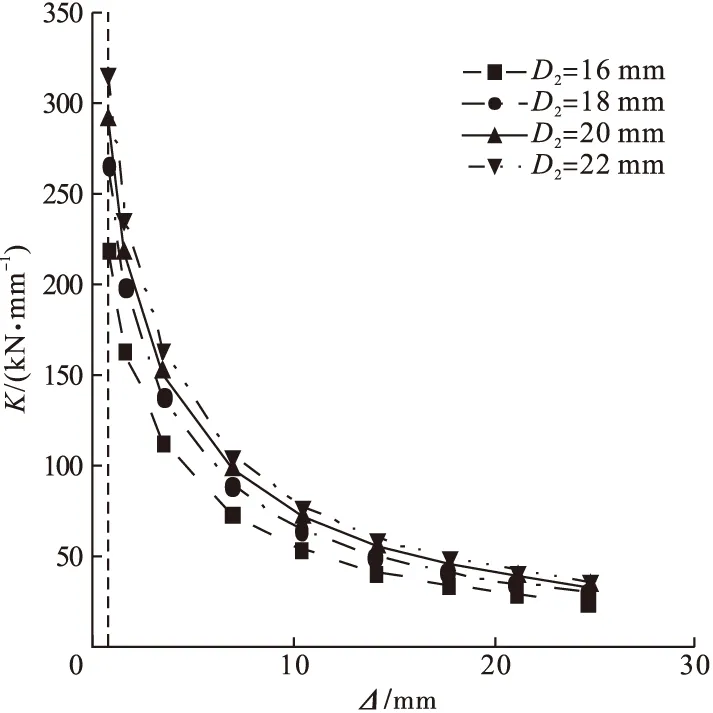
弹塑性阶段(AB段：46.1%Pu

平缓段(BC段：Pu

钢支撑达到极限应力后，加载点荷载-位移曲线位移增加的速率大于荷载增加的速率，B点、E点后荷载-位移曲线基本可以认为趋于水平，将B点、E点对应的荷载定义为新型节点的极限承载力，受拉侧和受压侧的极限承载力Pu分别为981.18 kN和919.42 kN，极限位移Δu分别为18.89 mm和19.59 mm。此时，钢支撑翼缘和高强螺栓产生了较大的塑性变形，对拉螺栓与钢管尚未达到极限应力，螺栓孔处及高强螺栓应力较大。

3.2 参数分析

笔者选取对拉螺栓直径、节点板厚度、方钢管柱厚度、高强螺栓直径，分析不同参数对新型节点承载力的影响，有限元结果见表2。

表2 各模型极限承载力Table 2 Ultimate bearing capacity of each model

从表2中可以得出：

(1)对拉螺栓直径每增加2 mm，节点受压侧的极限承载力分别提高2.3%、2.1%、0.1%，节点受拉侧的极限承载力分别提高3.1%、1.9%、1.8%。当直径从16 mm增加到24 mm时，节点受压侧和受拉侧的初始刚度分别提高了12.2%和14.8%。由此可见，对拉螺栓直径的增加对节点的承载力有提升的作用，直径从16 mm增加到18 mm时，极限承载力增幅最大。

(2)节点板厚度依次增大，受压侧加载点的极限承载力分别提高9.5%、4.2%、3.5%，受拉侧的极限承载力分别提高3.3%、3.1%、2.5%。节点板厚度不断增加，极限承载力提高的幅度减小，这是因为节点板厚度的增加使节点域应力分布更加均匀，减少了局部应力集中，因此实际工程中可以通过增大节点板厚度改善节点的承载力。

(3)方钢管柱壁厚度从8 mm增加到14 mm，受压、受拉两侧的初始刚度分别增大5.2%和5.4%；两侧的极限承载力分别增大1.4%和2.9%。改变钢管的厚度，基本不影响节点的极限承载力和初始刚度。

(4)高强螺栓的直径每增加2 mm，受压侧加载点极限承载力分别提高19.3%、19.7%、12.4%；受拉侧加载点极限承载力分别提高23.9%、12.0%、18.5%；节点的初始刚度也有较大的提升。增大高强螺栓直径极限承载力呈增大趋势，这是因为高强螺栓直径增加使节点域刚度增大。因此在实际工程中选用合适的高强螺栓直径对节点的极限承载力的改善有着显著影响。

4 滞回性能分析

4.1 加载制度

为研究新型节点的滞回性能，对新型节点进行往复加载。根据《建筑抗震试验规程》(JGJ/T 101—2015)[17]，加载制度见图5。

图5 加载制度Fig.5 Regime of loading

4.2 DB-3模型滞回曲线和骨架曲线

DB-3模型的荷载-位移滞回曲线如图6所示。从图中可以看出，两条滞回曲线基本重合，上下支撑力学性能相似，后续参数分析只选取上部支撑进行分析。滞回曲线较为饱满，呈现“弓型”，说明曲线具有“捏缩”效应，这是由于建模时高强螺栓杆的半径比螺栓孔小1 mm，二者之间存在间隙，加载过程中两个构件产生滑移。

图6 DB-3模型滞回曲线Fig.6 Hysteresis curves of DB-3

DB-3模型的荷载-位移骨架曲线如图7所示。从图中可以看出，骨架曲线与单调荷载作用下的荷载位移曲线走势大致相同。上侧钢支撑骨架曲线，在位移达到1.7 mm前处于弹性工作状态，骨架曲线基本为直线；正向、负向位移达到21.1 mm、21.2 mm后，位移增加的速率大于荷载增加的速率，定义21.1 mm、21.2 mm对应的荷载为正向和负向极限荷载。

图7 DB-3模型骨架曲线Fig.7 Skeleton curves of DB-3

4.3 参数分析

4.3.1 对拉螺栓直径

(1)耗能能力

不同对拉螺栓直径(D1)下各模型等效黏滞阻尼系数he对比如图8所示。从图中可以看出，对拉螺栓直径每增加2 mm，各模型等效黏滞阻尼系数峰值分别提高2.4%、7.0%、3.5%，在18～20 mm时增幅最大。对拉螺栓直径对节点弹性阶段的耗能能力影响较小，对弹塑性阶段耗能能力影响较大。各模型在位移达到15 mm左右时，等效黏滞阻尼系数大幅降低，这是由于高强螺栓的螺帽与节点板之间产生了滑移。

图8 不同对拉螺栓直径等效黏滞阻尼系数Fig.8 Comparison of energy dissipation coefficient

(2)刚度退化

笔者采用割线刚度K来研究节点的刚度变化，不同对拉螺栓直径(D1)下各模型刚度退化曲线如图9所示。

图9 不同对拉螺栓直径刚度退化曲线Fig.9 Comparison of stiffness degeneration curves

从图中可以看出，对拉螺栓直径对刚度退化曲线的形状基本没影响，节点屈服前，刚度退化速率较快，节点屈服后，曲线斜率变小，刚度退化速率变缓。对拉螺栓直径从16 mm增大到22 mm，各模型的初始刚度分别为276.9 kN/mm、281.9 kN/mm、290.6 kN/mm、301.8 kN/mm。由此可见，增大对拉螺栓直径节点的初始刚度呈降低趋势，这是由于增大螺栓直径，增大了栓孔引起的截面削弱。

(3)延 性

不同对拉螺栓直径(D1)各模型的延性系数见表3。从表中可以看出，各模型延性系数均大于4，说明新型节点延性较好[18]。从表2可知，随着对拉螺栓直径的增加，延性呈降低趋势，当D1=16 mm时，延性最优。

表3 不同对拉螺栓直径延性系数Table 3 Ductility factor of different bolt diameters

4.3.2 节点板厚度

(1)耗能能力

不同节点板厚度(Bb)各模型的等效黏滞阻尼系数对比如图10所示。

图10 不同节点板厚度等效黏滞阻尼系数Fig.10 Comparison of energy dissipation coefficient

从图中可以看出，弹性阶段各模型耗能能力相差较小，进入塑性后，曲线差别较为明显；随着节点板厚度的增加，等效黏滞阻尼系数逐渐减小，并且降低的幅度逐渐减小。节点板厚度由16 mm增加到18 mm时，等效黏滞阻尼系数降低了4.1%；由20 mm增加至22 mm时，等效黏滞阻尼系数仅降低了1.4%。

(2)刚度退化

不同节点板厚度(Bb)下各模型刚度退化曲线如图11所示。从图中可以看出，各模型的刚度退化趋势基本一致。随着节点板厚度的增加，初始刚度从290.6 kN/mm增大到327.5 kN/mm，这是因为节点板厚度的增加使节点域应力分布更加均匀，减少了局部应力集中。因此实际工程中可以通过增大节点板厚度改善节点的初始刚度。

图11 不同节点板厚度刚度退化曲线Fig.11 Comparison of stiffness degeneration curves

(3)延 性

不同节点板厚度(Bb)下各模型延性系数见表4。

表4 不同节点板厚度延性系数Table 4 Ductility factor of different plate thickness

从表中可以看出，与DB-3模型相比，各模型延性系数变化了+0.6%、+1.6%、+3.9%，说明增大节点板厚度有利于提高节点的延性。

4.3.3 方钢管柱壁厚

(1)耗能能力

不同方钢管柱壁厚度(Bz)下各模型等效黏滞阻尼系数对比如图12所示。从图中可以看出，各模型的等效黏滞阻尼系数曲线基本重合，方钢管柱壁厚度从8 mm增加到12 mm时，等效黏滞阻尼系数峰值仅增大了1.5%。说明增大方钢管柱壁厚度可以提高节点的耗能能力，但增幅较小。

图12 不同方钢管柱壁厚等效黏滞阻尼系数Fig.12 Comparison of energy dissipation coefficient

(2)刚度退化

不同方钢管柱壁厚度(Bz)下各模型刚度退化曲线如图13所示。

图13 不同方钢管柱壁厚刚度退化曲线Fig.13 Comparison of stiffness degeneration curves

从图中可以看出，方钢管柱壁厚度从8 mm增加到14 mm时，节点的初始刚度由288.1 kN/mm增大到292.4 kN/mm，仅提升了1.4%。这是因为节点域中方钢管柱主要作用为固定钢板，因此提高用钢量对节点的初始刚度贡献较小。

(3)延 性

不同方钢管柱壁厚度(Bz)下各模型延性系数见表5。从表中可以看出，各模型延性系数相差均在0.7%之内，表明方钢管柱壁厚度的变化对延性影响较小。

表5 不同方钢管柱壁厚延性系数Table 5 Ductility factor of different square steel tube wall thickness

4.3.4 高强螺栓直径

(1)耗能能力

不同高强螺栓直径(D2)下各模型等效黏滞阻尼系数对比如图14所示。

图14 不同高强螺栓直径等效黏滞阻尼系数Fig.14 Comparison of energy dissipation coefficient

从图中可以看出，对拉螺栓直径对节点弹性阶段的耗能能力影响较小，在弹塑性阶段耗能能力相差较大。高强螺栓直径每增加2 mm，各模型的等效黏滞阻尼系数峰值分别降低7.4%、2.2%、1.8%。由此可见，高强螺栓直径在16～18 mm变化时对节点的耗能能力较大；当直径大于18 mm时，增大高强螺栓的直径对节点的耗能能力影响较小。

(2)刚度退化

不同高强螺栓直径(D2)各模型刚度退化曲线如图15所示，各模型初始刚度分别为218.6 kN/mm、264.8 kN/mm、290.6 kN/mm、315.7 kN/mm。从图中可以看出，各模型刚度退化曲线差别较大，但其退化趋势基本一致。初始刚度随着高强螺栓直径的增加而增加，直径每增加2 mm，节点的初始刚度增幅都会减小。高强螺栓直径从16 m增加到18 mm时，初始刚度增幅最大，为21.1%；在18～22 mm时，直径每增加2 mm，初始刚度仅提升9%左右。

图15 不同高强螺栓直径刚度退化曲线Fig.15 Comparison of stiffness degeneration curves

(3)延 性

不同高强螺栓直径(D2)下各模型的延性系数见表6。从表中可以看出，高强螺栓直径从16 mm增加大22 mm，延性系数仅降低了1.1%，表明增大高强螺栓的直径会小幅降低节点的延性。

表6 不同高强螺栓直径延性系数Table 6 Ductility coefficient of different diameters of high-strength bolts

5 结 论

(1)单调荷载作用下节点的破坏模态表现为钢支撑首先达到极限承载力，随后高强螺栓达到极限承载力，二者均产生较大的塑性变形。

(2)在低周往复荷载作用下，新型节点的滞回曲线较为饱满，延性系数均大于4，表明新型节点具备良好的抗震性能。

(3)新型节点的承载力和初始刚度受高强螺栓直径变化的影响较大，耗能能力和延性受对拉螺栓直径变化的影响较大。

(4)为充分发挥节点的抗震性能，建议对拉螺栓的直径控制在16～20 mm；节点板厚度控制在16～20 mm；高强螺栓直径控制在18～22 mm。