利用双光栅衍射测量微谐振动的研究

肖国宏，钟锡华 ,刘 萍

(1. 西安交通大学 理学院，陕西 西安 710049；2. 北京大学 物理学院，北京 100871)

光栅是一种广泛应用的光学器件。由两个相距一定距离的光栅所构成的双光栅器件则拓展了光栅的应用领域[1]. 2108年诺贝尔物理学奖授予的激光脉冲放大技术，先后在实验中使用了两对双光栅，先后起到压缩谱宽和扩展谱宽的作用，从而为超快超强激光提供了技术支持[2].

本文以基元光栅即余弦光栅为研究对象，运用波前相因子分析方法，给出了具有一定距离的双余弦光栅衍射光斑的强度公式，从中可以看出衍射场之间的干涉效应，乃是两列或三列衍射平面波之间的相干叠加结果. 进而，当两个光栅之一作纵向或横向微振动时，由于衍射场内在的干涉效应，导致0级、±1级衍射斑的强度信号呈现出复合余弦型函数变化规律.通过数学分析得出光栅在微谐振动的一个周期时段内，信号强度极值点出现的时间与微谐振动振幅的函数关系. 这种关系奠定了利用双光栅测量和研究微振动理论基础. 也为研究其他双光栅异化结构及其运动的衍射场，提供了一种可以借鉴的理论工具.

1 理论推演

设有两个相同的一维余弦光栅G1、G2平行放置，如图1所示.

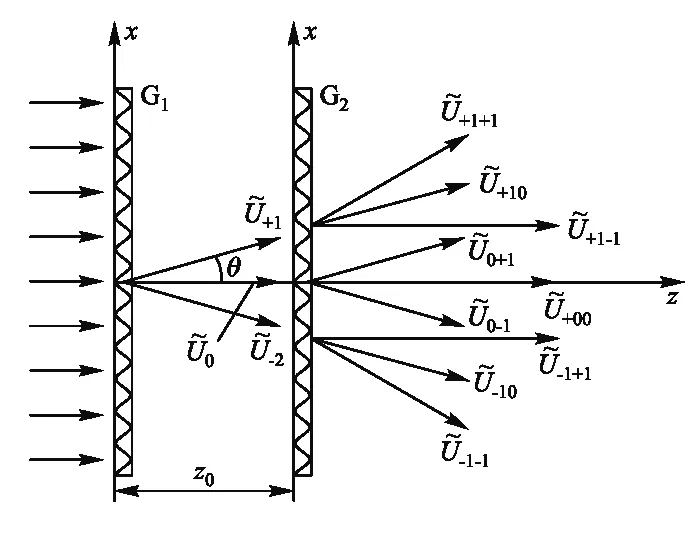
图1 双光栅衍射示意图(每一个箭矢代表一列衍射平面波)

两个光栅的空间周期均为d1,其纵向间隔为z0，设其屏函数分别为：

(1)

(2)

其中f1=1/d1，为光栅的空间频率.现用一束单色平面波正入射到第一个光栅G1，该平面波的振幅为A，波长为λ，其波数k=2π/λ. 这束平面波通过光栅G1后，其波函数变为

(3)

运用波前相因子分析法[3-5],便可判定上述波前包含3列平面波成分，即

(4)

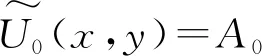
(5)

代表一列正出射平面波：

(6)

代表一列沿θ1方向斜出射平面波：

(7)

代表一列沿-θ1方向斜出射平面波.这里

(8)

这3列平面波向前传播z0距离到达第二个光栅G2，此时3列平面波的波前分别为：

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

2.1 各方向平面波的相干叠加强度

在上述式(14)—式(22)中所展示的9列衍射平面波如图1所示，沿θ=0方向有3列平面波，它们合成的复振幅为

(24)

沿θ=θ1方向有2列平面波，其合成的复振幅为

(25)

同理，沿θ=-θ1方向也有2列平面波，其合成复振幅为

(26)

沿θ=θ2和θ=-θ2方向各有一列平面波

(27)

(28)

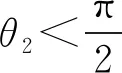
(29)

(30)

(31)

δ(z0)≡kz0(1-cosθ1)

(32)

当利用凸透镜汇聚这5个方向的衍射平面波，在透镜的焦平面上会得到5个衍射斑，称为夫琅禾费衍射斑.但是只有I0和I±1是平面波相干叠加的结果.换言之，双光栅纵向间隔的变化只会反映在式(29)和(30)所表示的0级和±1级衍射斑中，这是实验上可以观测到的有变化的相对光强.

2.2 光栅G2作纵向微谐振动时衍射斑的强度

(33)

衍射光强式(29)和(30)中余弦项的相位可表示为

(34)

其中

β≡(1-cosθ1)

(35)

由式(29)、(30)可得0级和±1级衍射斑的光强为

(36)

(37)

式(36)和(37)中的相对光强变化均为一个复合余弦函数，记为

(38)

由式(8)可知，当光栅常数远大于光波波长时

(39)

(40)

(41)

2.3 光栅G2作横向微谐振动时衍射斑的强度

当光栅G2相对于G1沿x轴的横向位移量为x0，于是，G2的屏函数被改写为

t0+t1cos(2πf1x-δx)=

(42)

这里，相移量：

δx≡2πf1x0

(43)

这表明G2的横向位移，导致其屏函数的相移，从而会导致通过它后面的衍射斑会有等量的相移δx.

(44)

(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

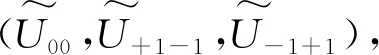
(53)

其模的平方给出0级衍射光斑强度：

γ2cos(2πf1x0)cos(kz0-kz0cosθ1)]

(54)

在θ=θ1和θ=-θ1方向各有两列平面波，其合成复振幅分别为

(55)

(56)

其模平方分别给出±1级衍射光斑的强度

(57)

(58)

当光栅G2作横向简谐微振动时

x0(t)=acosω0t

(59)

将式(59)代入式(54)、(57)、(58)，即可得到0级和±1级衍射斑的强度信号：

γ2cos(2πf1acosω0t)cosα]

(60)

(61)

(62)

这里

α≡kz0(1-cosθ1)

(63)

当光栅常数远大于光波波长时，由式(39)可得

(64)

对于式(60)所表示的0级衍射斑光强已有很明确的分析了[6].而±1级衍射斑相对光强的变化仍然是一个复合余弦函数，只是多了一个初相位.这里选择+1级中的复合余弦函数作为分析对象，可表示为一般的函数形式：

(65)

这个函数与表示纵向微谐振动相对光强变化的式(41)具有相同形式.

显然这是一个周期函数，当x在[0,2π]范围内变化时，复合余弦函数值y关于x=π点是对称的.因此将此函数定义域设定在[0，π].在这个区域中，函数y的极值点可由下式

(66)

得到 sinx=0

(67)

(68)

求解这两个方程可以得到y取极值的坐标点为

x=k′π,k′=0,1

(69)

(70)

由式(70)确定k的取值范围为

(71)

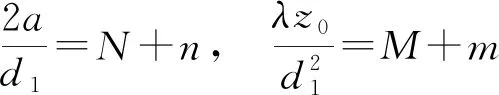
(72)

其中N、M为正整数，n、m为正纯小数. 式(71)就可写为

-N+(m-n)≤-k-M≤N+(m+n)

(73)

k值的个数可以分为以下4种情况:

当m-n>0,m+n<1,k可取2N个极值点；

当m-n>0,m+n≥1,k可取2N+1个极值点；

当m-n≤0,m+n<1,k可取2N+1个极值点；

当m-n≤0,m+n≥1,k可取2N+2个极值点.

考虑到内余弦函数cosx在[0，π]区间内是单调减函数，由式(70)确定的第一个极值点发生在

k=-M+N，当m-n>0；

k=-M+N+1，当m-n≤0.

设第1个极值点的坐标为x1，第r个极值点的坐标为xr，由式(70)可得

(74)

由此式就可以计算出光栅G2的振幅了.考虑到在实验中观测到的极值点的坐标是时间量，所以设

(75)

T0为光栅G2谐振动的周期，它和T1、Tr都是可观测量.由这些量可以计算得到光栅振幅的表达式：

(76)

以上所提到的极值点不包含式(69)所定义的两个端点极值.对于-1级衍射斑极值点的个数和光栅振幅的计算公式是相同的. 式(76)就是利用双光栅测量微谐振动振幅的基本公式.

由式(72)可以看到

(77)

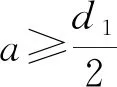
(78)

式(78)给出了利用双余弦光栅测量微谐横向振动的最小振幅，即测量的精度.

同理可由式(41)分析出光栅G2做纵向微谐振动时，振幅的计算公式为

(79)

与式(72)、(77)同理可得

(80)

此式说明了利用双余弦光栅测量纵向微谐振动的振幅应不小于亚毫米.很明显对于一对相同的双余弦光栅，测量纵向振动的精度要远小于测量横向振动的精度，而且振幅的测量与所使用光的波长有关.

3 数值计算

设光栅G2固定在一个驱动频率约为500 Hz的音叉上，数值计算参数如下：两个余弦光栅常数:d1=0.01 mm；所使用的半导体激光器波长:λ=635×10-6mm；双光栅的间距z0=5.00mm.

由以上参数可计算出

当x=2π·500t的变化范围为0到2π时，由式(65)得到+1级衍射光斑强度相对变化如图2实线所示.图中虚线为音叉在一个周期的归一化简谐振动曲线，即内余弦函数. 基于我们对N，n,m的分析，显然光栅在一个周期的振动过程中，+1级衍射相对光强在(0,π)区间内有6个极值点.

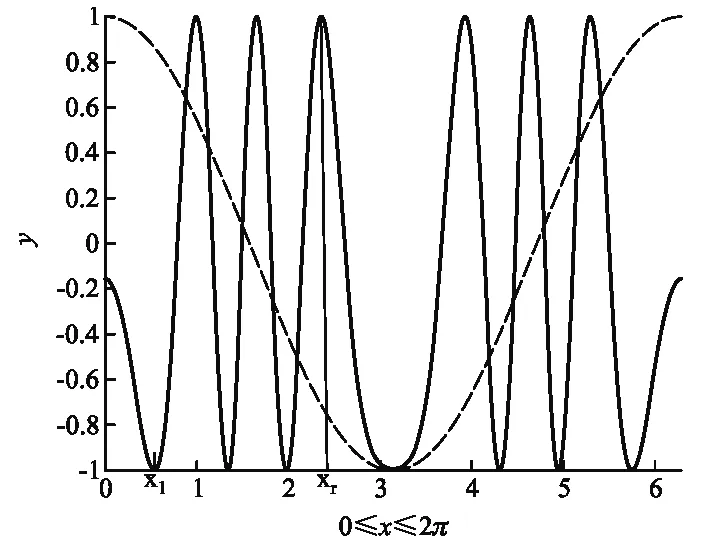
图2 双光栅相对横向振动时+1级衍射斑光强变化曲线y=cos(3.2πcos x-31.75π),虚线表示内余弦函数cos x

在实验中探测到的+1级衍射光强的变化在示波器上如图3所示。只要测量第1个极值点的坐标为x1和第r个极值点的坐标为xr所对应的时间量T1和Tr，以及光栅振动的一个周期T0，就可以利用(76)式计算出光栅的振幅.

图3 双光栅相对横向谐振动时+1级衍射斑光强变化实测曲线

如果设双光栅的衬度比γ=t1/t0=1，可由式(60)得到0级衍射光斑强度变化，如图4所示.

图4 双光栅相对横向振动时0级衍射斑光强变化曲线y=0.25cos2(3.2πcos x)+cos(3.2πcos x)cos31.74π,点划线表示复合余弦函数cos(3.2πcos x)，虚线表示内余弦函数cos x

在图4中可以看出，复合余弦函数平方项又四分之一的存在改变了复合余弦函数(点划线所示)的起伏，但没有改变极值点的位置和图形分布的对称性.所以仍然可以用来测量光栅的横向振幅，但由于cosα项和复合余弦函数相乘的关系，可能降低0级光斑强度变化的幅度，所以不建议使用0级衍射光斑探测双光栅的相对横向振动.

对于光栅G2做纵向微谐振动的数值模拟和横向微谐振动的情况有相同的结论.所不同的是式(80)对纵向振动振幅的要求较式(78)要大的多.如果纵向微振动的振幅不能满足式(80)，由式(41)得到的纵向微振动0级和±1衍射斑相对光强变化则如图5所示.

图5 双光栅相对纵向谐振时衍射斑光强变化曲线虚线表示内余弦函数cos x

此时从观测到计算已不再适合利用双余弦光栅研究纵向微谐振动了.这也就是利用双余弦光栅衍射测量微谐振动精度限制的原因了.

当双光栅既有横向振动又有纵向振动时，可将式(33)代入到式(65)，得到

(81)

当光栅在纵、横方向同时做简谐振动时，+1级衍射光斑强度变化如图6所示. 实线为同频率且初相差θ=0时的曲线；虚线表示同频率但初相差θ=0.1π的曲线.显然波形对初相是很敏感的.

图6 光栅同时做纵、横向同频谐振动时+1级的相对光强变化,实线为初相差θ=0时的曲线,虚线为初相差θ=0.1π的曲线

当两种振动的频率不同而初相差为0时，+1级的相对光强变化曲线如图7所示.

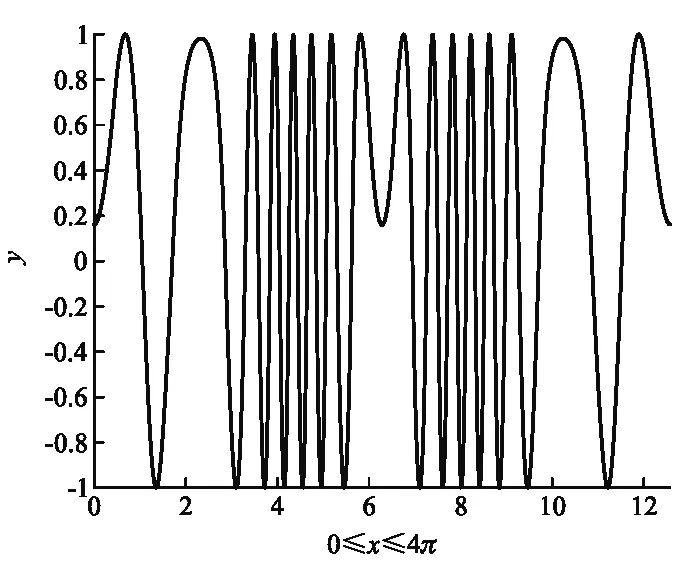
图7 光栅同时做纵、横向不同频谐振时+1级的相对光强变化,此时x=0.5x′,θ=0

在以上两种情况中，纵、横方向的振动是没有办法分开讨论的.

4 结论

运用波前相因子法，分析双余弦光栅衍射场的干涉是方便而有效的.尤其在分析中考虑到了双光栅之间的间距，避免了双光栅密接情况下横向振动分析结论的局限性[6].利用双余弦光栅衍射光斑强度所展现的复合余弦函数的特点，可以用来研究微谐振动的振幅和频率，如式(76).并明确给出了纵、横向谐振振幅测量精度的限度，如式(78)，(80).对于非余弦型光栅，可以利用傅里叶级数展开为多个余弦函数之和，本文中的结论仍然是可以利用的.

对于双光栅之间的非谐振情况的分析将是我们进一步研究的内容.