FBG应变挠度法标定及过程仿真
侯俊凯,刘 冰,崔建军,魏晋和,陈 恺,张 鹏,李学峰
(1.山东科技大学机械电子工程学院,山东青岛266590;2.中国计量科学研究院,北京100029;3.天津大学精密仪器与光电子工程学院,天津300072;4.国电电力发展股份有限公司,北京600795)
1 引 言
光纤布拉格光栅(fiber Bragg grating,FBG)应变传感器(简称FBG传感器)是以光纤为介质,对测量结构的应变以光信号的变化输出的新型传感器。它具有柔性好、安装轻便、抗电磁干扰能力强、动态范围大、灵敏度高及可以分布式测量的优点,被广泛应用在健康监测、市政工程、石油工程、智能材料等领域[1~4]。
考虑到FBG传感器目前的应用需求广泛,但在测量精度方面尚有待提高,生产厂家给出的FBG传感器精度指标通常不大于1%,对其进行科学合理的高精度标定校准的 技术及方法十分重要。常用的FBG传感器标定方法有弯曲梁实验法(四点弯矩梁法、等强度悬臂梁法)[5,6]、试验机拉伸法[7]和特殊专用标定方法[8],但能够实现高精度的标定方法较少,标定偏差很多均在5%~20%[9,10]。例如,有的弯曲梁实验法经仔细分析验证后,实际得到的梁表面应变不确定度在15%以上[11]。弯曲梁实验法因通过梁的弯曲变形而产生应变,还会存在胶粘剂和封装基片的厚度等导致FBG传感器感知的应变大于梁表面应变的情况[12],相应的应变比例放大系数估算是否准确对标定精度也有影响。同时,在梁到FBG传感器的应变传递过程中,胶层的柔性和厚度也会影响应变的传递效率[13~18]。例如,陈昊等[15]得到未封装FBG传感器应变灵敏为0.919 pm/×10-6,而基片式封装的FBG传感器的应变灵敏度为 0.822 pm/×10-6,Li H等[17]以环氧树脂353 ND有机胶和焊锡粘接层作为胶粘剂,分别得到平均应变传递效率为89.8%和99.2%。应变传递效率理论机理较为复杂[19],理论模型较多,准确性难于验证估计,相对而言,有限元分析在充分获取材料及结构的信息条件下,也容易获得较为准确的结果[15,20]。至今尚缺少体系化的高精度可溯源的FBG传感器标定方法。
目前等强度悬臂梁法具有结构简单、稳定性好,对FBG传感器粘贴位置要求不严格[21],应用较为普遍的优点。常采用力学加载的方法实现梁的弯曲,从而在梁的表面产生应变。由于梁的尺寸误差及材料微观结构的均匀性等均会影响梁的实际力学特性,使得该种标定方法与多项具体材料特性相关,溯源困难,难以实现高精度。针对这些问题,本文提出一种基于多点挠度法的FBG应变标定的思路,通过测量等强度悬臂梁挠度的变形量来解算梁的表面应变,避免了梁的力学特性估算不精确对梁表面应变的测量影响,进而实现FBG应变的精确标定。
首先,设计了基于挠度法的FBG应变测量装置,并针对等强度悬臂梁的工作特性进行了分析;然后,采用有限元技术分析了梁受力变形时的应变分布状态以及应变与挠度的相关性,还仿真分析了蝶形封装FBG传感器的应变传递效率;最后,进行了基于挠度法的蝶形封装FBG应变测量试验,给出了整套体系化的不确定度评定方法。
2 装置设计及理论分析
2.1 装置设计
应变测量装置如图1所示。等强度悬臂梁是钢材料,其弹性模量范围为190~220 GPa,受力后其表面会产生应变;水平仪用于确定梁的水平状态;砝码的精度等级为M1级,共5个,每个砝码的重量为5.00 N,用于改变梁的受力状态和产生应变;精密位移计由测头和信号处理系统组成,分辨力为1 nm,在其量程25 mm内,示值误差为±0.1 μm,用于测量梁的挠度和厚度,且能够在等强度悬臂梁的任意位置处进行挠度测量;FBG传感器粘贴在梁上,用于测量梁的表面应变;FBG解调仪的波长准确度为1 pm,波长范围为1 510~1 590 nm,可以读取FBG传感器的输出波长值。
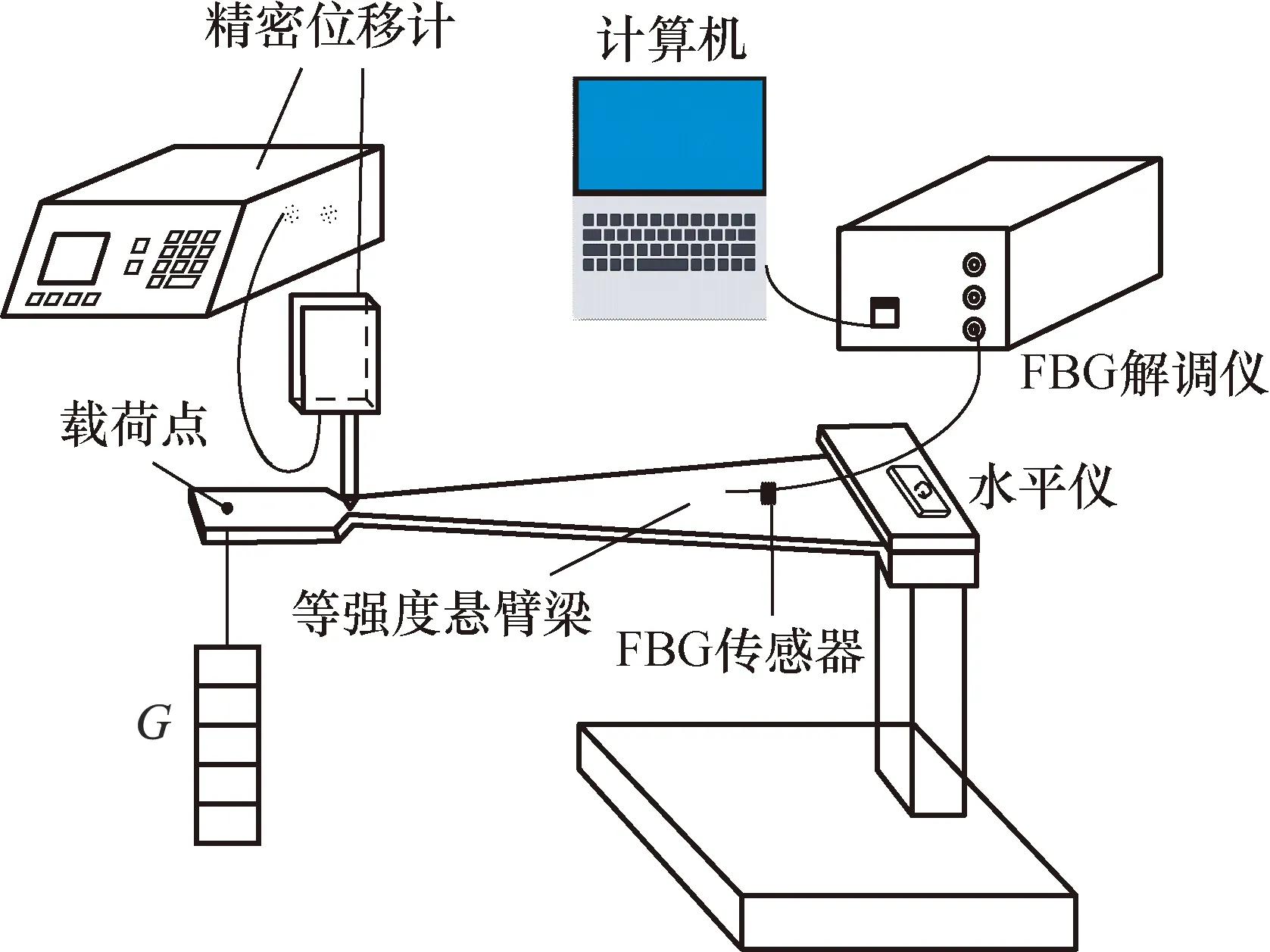
图1 应变测量装置图Fig.1 Strain measuring device drawing
装置的优势在于砝码与精密位移计结合能够得到梁在应变测量时的弹性模量,可为应变传递过程提供更为精确的应变传递效率,进而提高标定的准确程度。
2.2 理论分析
FBG传感器的应变特性采用等强度悬臂标定时,需要先根据梁的尺寸及材料参数及加载载荷量等,对其表面应变进行理论分析,然后通过FBG传感器波长变化来反映FBG传感器的应变灵敏度。
2.2.1 等强度悬臂梁应变测试原理
等强度悬臂梁的一个特点是在其载荷点上加一个载荷G后,距载荷点距离x的断面(矩形较为常见)上的表面应力(简称应力)为恒量,且符合公式(1):
(1)
式中:bx为梁的宽度;h为梁的厚度。
对式(1)进行变换,得到:
(2)
由式(2)可知,梁的宽度bx随距离x的变化而变化,变化的斜率为
(3)
而沿梁轴线方向的表面应变值,即梁的表面应变εx为:
(4)
式中:b0为梁的最大宽度值;L为梁的有效长度;E为材料的弹性模量。
由式(4)可知,对于特定的等强度悬臂梁,εx与载荷G成正比。
等强度悬臂梁上任意一点(载荷点除外)的挠度可表示为
(5)
联立式(4)和(5),得到:
(6)
对于特定的等强度悬臂梁而言,依据式(4),即采用力学加载的方法原理,需要精确知道梁的弹性模量,但往往采用的仅是该类材料弹性模量的参考值,所以影响梁表面应变计算的准确性。
依据式(5),可以通过挠度值和相关几何尺寸及载荷值反推得到梁的弹性模量值。
依据式(6),应变可以通过挠度计算得到,而无需已知梁的弹性模量。这对应变测量而言,通过精确的等强度悬臂梁的尺寸及其挠度变形量,即可以获得εx值。
2.2.2 FBG传感器工作机理
对于FBG传感器,有如下关系式:
λB=2neffΛ
(7)
式中:λB是FBG发生布拉格衍射的中心波长值;Λ、neff分别是光栅的周期和有效折射率。
不考虑温度影响的情况下,应变与波长可由式(8)线性关系描述[19]:
=(1-pe)ε
(8)
式中:Δλ为波长变化量;p11,p12均为光纤的弹光系数;μg为光纤的泊松比;Pe为光纤的有效弹光系数;ε为FBG传感器的应变。对于熔融石英光纤来说,通常取p11=0.121,p12=0.27,μg=0.17,neff=1.456。
假设中心波长为1 530 nm时,结合式(8)可得应变灵敏度Kε=λB(1-pe)=1.20 pm/×10-6,该计算方法是从光纤光栅的光学原理得到的应变灵敏度,与光纤光栅的材料及工艺相关,且经过封装后的FBG传感器的性能又会发生变化,因此,Kε的标定需要通过特定的应变测量装置实现。式(8)也可以写为
Δλ=Kεε
(9)
式(9)为经应变测量装置后通过基体(如等强度悬臂梁)的表面应变进而得到FBG传感器的感知应变,从而标定得到FBG传感器的应变灵敏度,由于Δλ与ε成线性关系,而等强度悬臂梁的表面应变与载荷成正比,因此,可以通过加载一系列载荷改变梁的表面应变和FBG传感器的应变来标定FBG传感器。
2.2.3 FBG感知应变计算原理
当FBG传感器粘贴于等强度悬臂梁的工作表面上,由于梁的弯曲会导致FBG传感器实际的应变比梁的表面应变大。参照文献[13,19]中的计算方法,得到应变比例放大系数α:
(10)
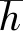
又由于FBG传感器的柔性组件以及粘贴胶层的柔性,使得FBG传感器的应变感知力降低,故采用应变传递效率β表示。
考虑上述参数,给出FBG传感器感知的应变值与相应的梁表面应变具有如下关系:
ε=βαεx
(11)
3 FBG应变仿真
首先采用Abaqus软件对梁的整体结构的挠度、应变等进行有限元分析,验证挠度法的准确性;其次根据实际测量得到的相关参量,进一步精确建模和仿真来研究FBG传感器的应变传递过程。
3.1 梁仿真
要实现FBG应变高精度标定,需要找到梁上理论公式无法得到的应变分布均匀的区域,并对挠度法应变测量的准确性进行分析。
3.1.1 建模及仿真
根据梁的几何尺寸及材料特性,表1为梁的仿真用的结构材料参数,依据参数对梁建模。等强度梁右端断面设置固定约束,左端载重,创建载荷点与附近表面进行耦合,通过施加集中力来模拟梁的载荷加载过程。

表1 梁仿真的结构参数Tab.1 Structural parameters of beam for simulation
开启分析步模块中的几何非线性来对等强度悬臂梁在载荷作用下产生位移和变形等非线性效应过程进行精确分析。划分后的网格如图2所示。

图2 等强度悬臂梁网格划分图Fig.2 Grid division drawing of cantilever beam of equal strength
仿真发现,理论上一定载荷下梁的表面的应变是相等的,但实际过程中,由于梁的外观结构等因素,导致了非均匀的应变区域的出现。如图3为载荷G=20.00 N时,192.0~196.0 μm/m的应变区域云图,可以看到不均匀区域主要集中在固定端附近,沿中轴线的长度约占梁有效长度的1/4。

图3 G=20.00 N时应变区域192.0~196.0 μm/m云图Fig.3 Shows the distribution pattern of 192.0~196.0 μm/m when G=20 N
通过图3可以较为精确地获得梁表面各点的应变分布情况。
3.1.2 应变仿真分析
仿真也可以查看不同载荷下的表面应变情况。表2为不同载荷下表面应变的理论计算值和仿真数值的对比,结果具有一致性。
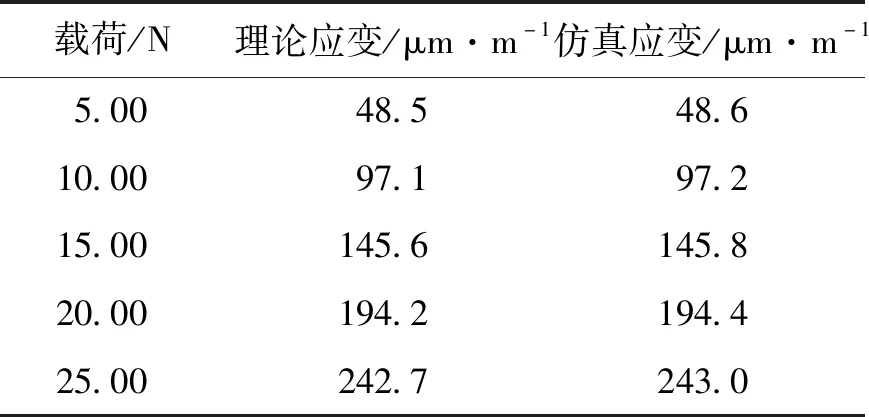
表2 理论应变与仿真应变对比Tab.2 Comparison of theoretical and simulated strain
图4给出G=20.00 N时梁的表面应变分布图,在弹性变形范围之内,其它载荷下梁的表面应变的分布状况均与图4类似。

图4 G=20.00 N时表面应变分布图Fig.4 Surface strain distribution when G=20.00 N
3.1.3 挠度仿真分析
挠度随着距载荷点的位置变化而变化。因此对挠度仿真表现为不同载荷下固定点分析和一定载荷下的不同位置分析。
图5为载荷G为0.00 N、5.00 N、10.00 N、15.00 N、20.00 N、25.00 N时,等强度悬臂梁的挠度云图。
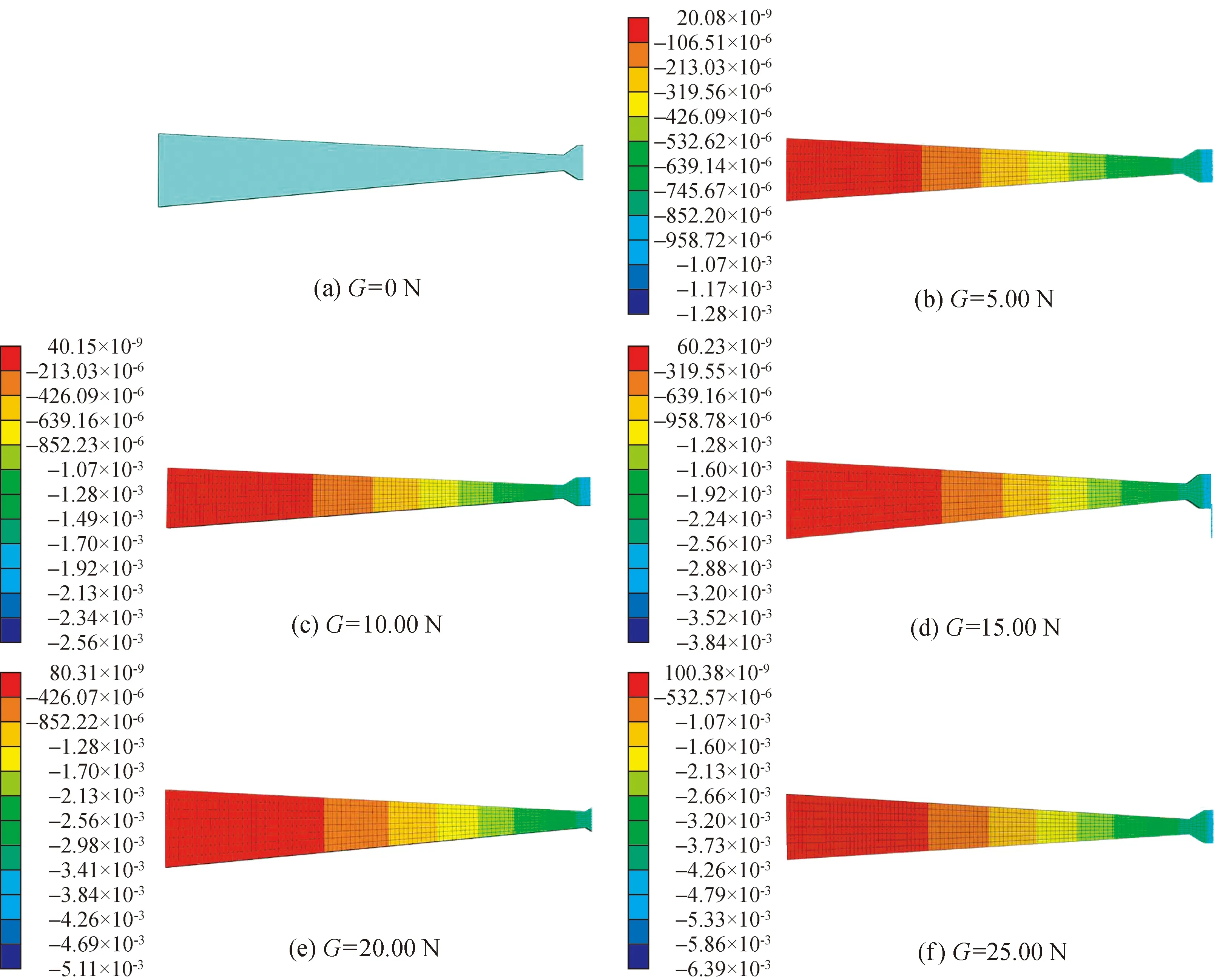
图5 不同载荷下梁的仿真挠度云图Fig.5 Simulated deflection cloud diagram of beam under different loads
分析发现:在特定位置x=75.00 mm处,在不同载荷下,得到梁的系列仿真挠度值,将它们带入理论公式(6),计算得到仿真挠度值对应的应变值,见表3。对比表2应变结果,容易发现3者结果相近。

表3 x=75.00 mm,仿真挠度及相应计算的应变值Tab.3 x=75.00 mm, simulation deflection and corresponding calculated strain value
其次,选择一定载荷下不同位置的挠度进行分析。仍以G=20.00 N为例,也将仿真挠度值与带入理论公式(6)计算得到的相应应变值, 见表4, 并进行分析。排除梁因结构等方面存在应变结果的微小差异以及应变不均匀区域(x=345.0 mm)外,各点处挠度对应的应变值与表2中载荷为20.00 N的理论应变和仿真应变相近,符合等强度悬臂梁的工作特性。

表4 G=20.00 N,距加载点不同的挠度仿真分析Tab.4 G=20.00 N, simulation deflection analysis of different distance from loading point
3.2 FBG传感器实验仿真
3.2.1 建模参数
精确测量了FBG应变传递过程中相关参量的几何尺寸,并结合梁、蝶形封装基片、胶、光纤的力学特性等的估算,给出的相关建模参数如表5所示。

表5 应变传递过程中影响参量的实际值Tab.5 Dimensions and structural parameters of beams
3.2.2 应变传递仿真分析
图6为G=20 N,FBG传感器局部仿真放大图。

图6 G=20 N,FBG传感器局部仿真放大图Fig.6 G=20 N, local simulation magnification of FBG sensor
蝶形封装FBG传感器两端部分为胶粘区域,中间是包含光纤光栅节的应变感知光纤段,仿真得到的FBG传感器应变即此处的中间部分的应变平均值。对其进行仿真后发现:两个长方形槽内侧与光纤光栅节的感知光纤段是应力应变集中区域。FBG传感器两端应变值(标距范围之外)很小,取中间应变均匀区域研究,得到FBG传感器的平均应变为FBG传感器的应变值。仿真得到如图7所示不同载荷下的梁表面到FBG传感器的应变传递效率在96.2%~96.5%之间,平均应变传递效率为96.32%。
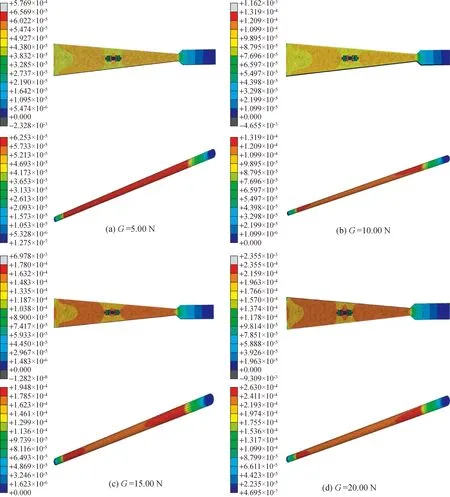
图7 不同载荷下FBG应变传递过程仿真图Fig.7 FBG strain transfer process simulation under different loads
4 实验分析
4.1 实验过程
应变测量装置调整图如图8所示。调节底座垂直旋钮,使水平仪的气泡居中,并将FBG传感器粘贴于应变均匀区域。

图8 应变测量装置调整图Fig.8 Strain gage adjustment diagram
环境温度在24.5 ℃,实验过程中的温度变化小于0.2 ℃。实验开始前,用精密位移计测得梁的厚度;实验过程中,精密位移计测得的数值稳定性约为0.01 μm。
实验1:保持载荷G=20.00 N不变,进行不同位置挠度的测量实验。选择不同的挠度测量位置,记录下测得的挠度值,同时用数显式游标卡尺测量精密位移计测头至载荷加载点(即x)的距离值。
实验2:保持精密位移计的测量位置不变,在不同载荷下测量各点的挠度和FBG传感器的波长值。载荷由0加载至25.00 N的过程中,每次加入载荷后,待悬臂梁相对稳定后,记录下精密位移计测得的挠度值与数显式游标卡尺测得的x值,同时记录下计算机显示的波长值,重复测量3次,完成实验数据的采集。
4.2 实验结果
首先分析载荷一定时,不同测量位置的挠度值,通过计算挠度得到梁的应变值。然后在不同载荷下,对某固定位置进行挠度测量,通过计算挠度得到的应变值,进一步分析得到FBG传感器的应变。
4.2.1 不同位置的挠度分析
图9为在G=20 N时,不同位置的弹性模量E的计算挠度值与实验挠度值结果比较。可以看出x在250.0~350.0 mm附近测得的挠度值偏大,印证了仿真的应变不均匀区域。
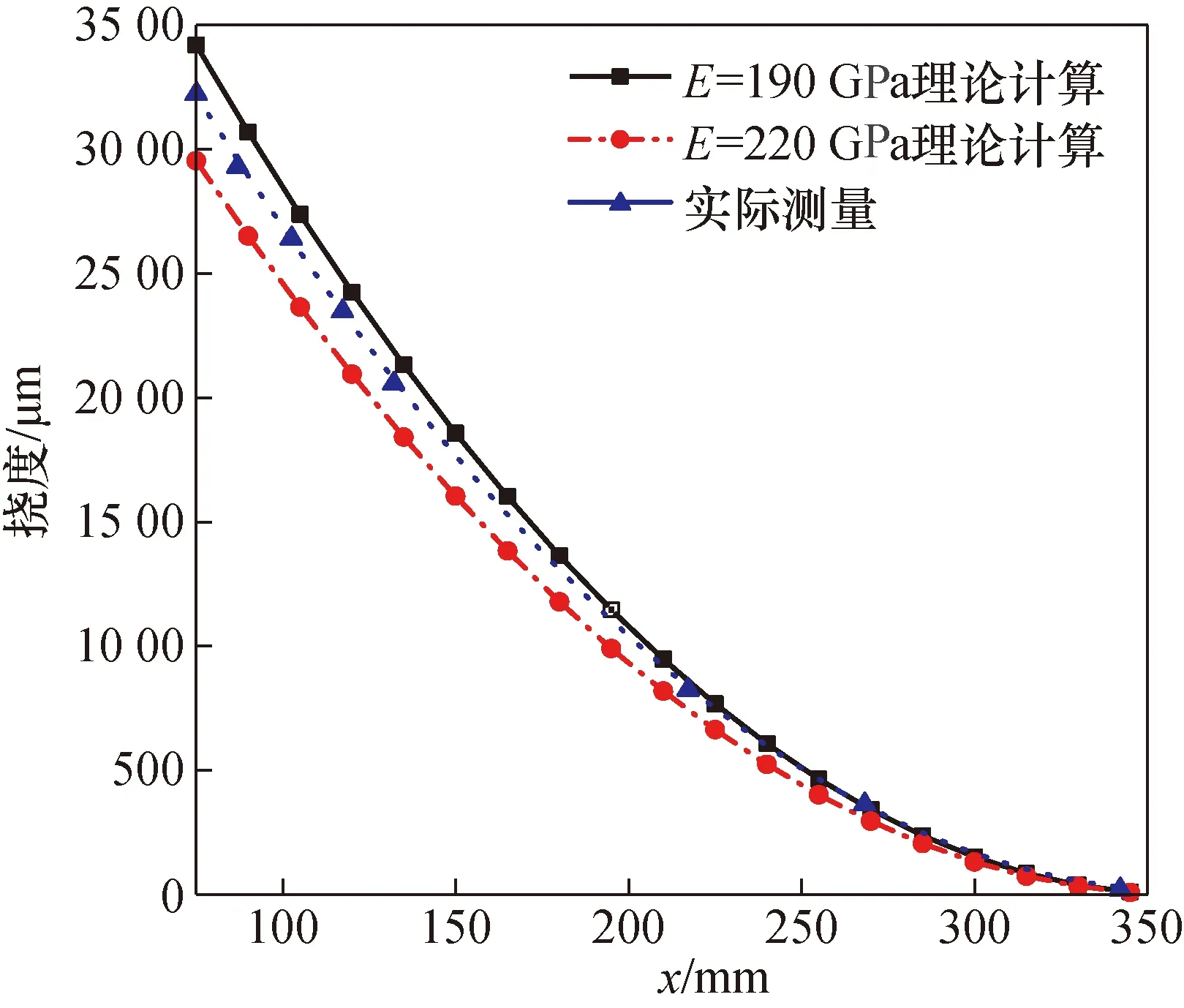
图9 G=20 N,不同位置的挠度分析Fig.9 G=20 N, deflection analysis of different positions
由于实验过程中载荷加载点和精密位移计的测头位置难以精确测量,导致x的测量误差偏大。为减小此处的误差,进一步对挠度测量位置展开研究发现:越靠近载荷点处,x点的位置偏差对应变测量结果的影响越小。比如对比x=75.0 mm与x=217.2 mm处两点测得的挠度值,当x变化为±1.0 mm 时,经式(6)计算得应变变化范围分别为5.7 μm/m和2.8 μm/m。因此,为减小x位置引起的应变误差,挠度测量点选择了距载荷加载点近的位置,故进一步选择x=75.0 mm处进行不同载荷下的挠度测量实验。
4.2.2 不同载荷的挠度分析
在不同载荷下,对x=75.0 mm位置处测得的3组挠度值分析。图10是测量的3组挠度与挠度测量线的偏差随载荷的变化情况。
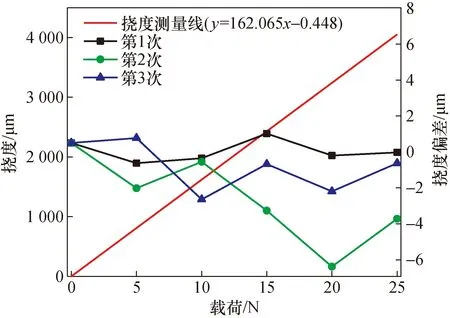
图10 不同载荷下测量的3组挠度值Fig.10 Three sets of deflection values measured under different loads
图11是根据力学加载的方法计算得到的梁表面应变及由3组挠度拟合计算得到的梁的表面应变对比图,图中测量挠度计算拟合直线为y=9.918 198 6x-0.026 535 0,相关系数达0.999 999 8。
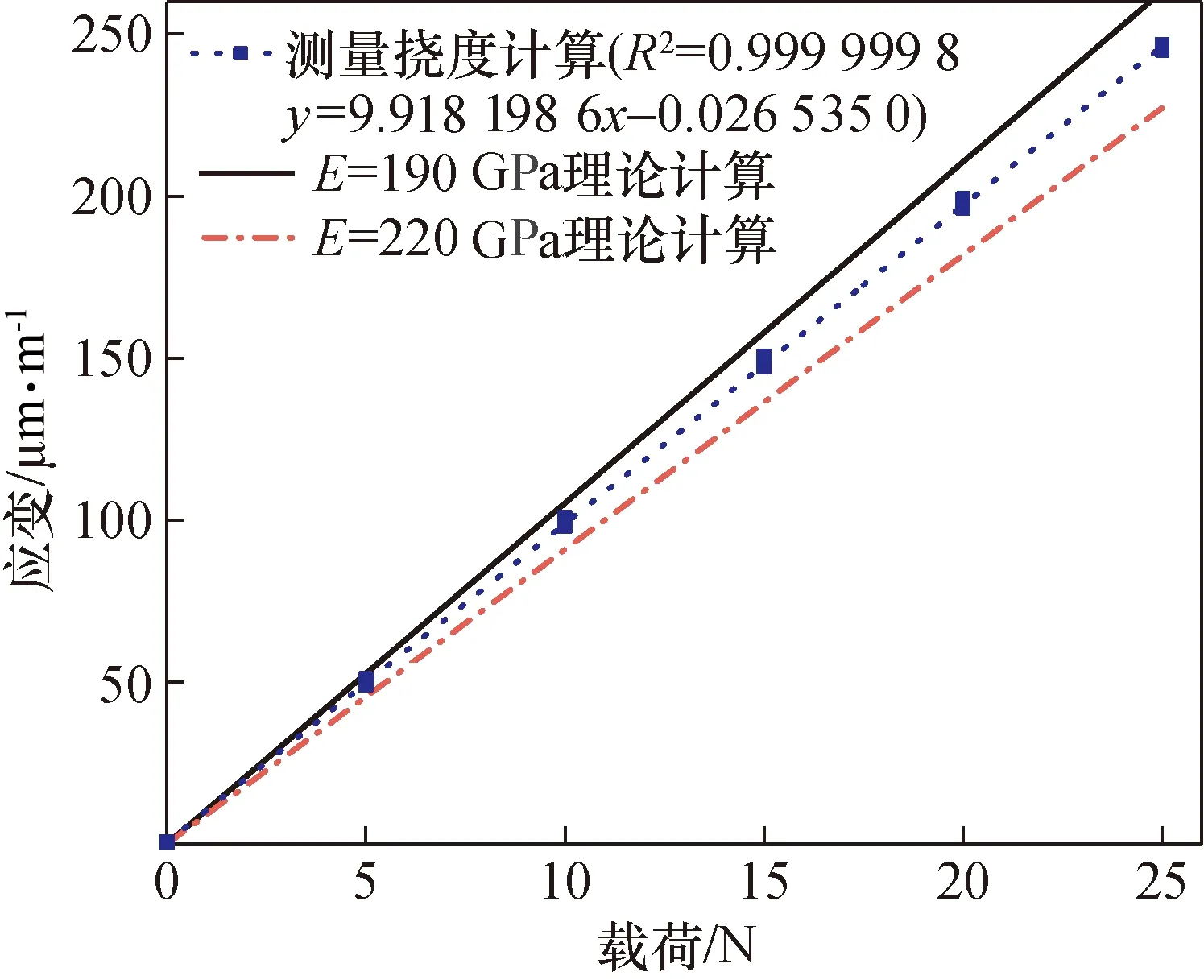
图11 理论计算及挠度测量的应变结果对比Fig.11 Comparison of calculation results of elastic modulus and deflection
由于力学加载的方法必须先精确得到梁的弹性模量,但弹性模量作为材料的一种特性,并非是固定值,它会随环境温度以及疲劳过程发生改变,且精确测量梁的弹性模量也较为困难。相对而言,挠度法可以在弹性模量未知的情况下直接获得梁的表面应变值,故挠度法优势明显,且根据式(5),可反推出该梁的弹性模量E=203.8 GPa。
4.3 FBG传感器应变测量结果
FBG传感器应变测量结果需要对胶粘剂、封装基片、光纤等微观结构进行精密的测量,因此使用影像仪测得梁与蝶形基片之间粘接胶的厚度、光纤下表面到蝶形基片的槽底的距离、光纤的半径、蝶形基片的厚度、蝶形基片上的槽深、标距。图12为光纤在影像仪下的测量过程图,在该仪器下光纤清晰可见。
图12 光纤在影像仪下的测量图Fig.12 Fiber under image instrument measuring
实验中挠度法计算得到梁表面应变,应变比例放大系数α=1.231 5,仿真得到的平均应变传递效率β=96.32%,经式(11)计算得FBG传感器应变。表6为FBG传感器应变的测量结果图。
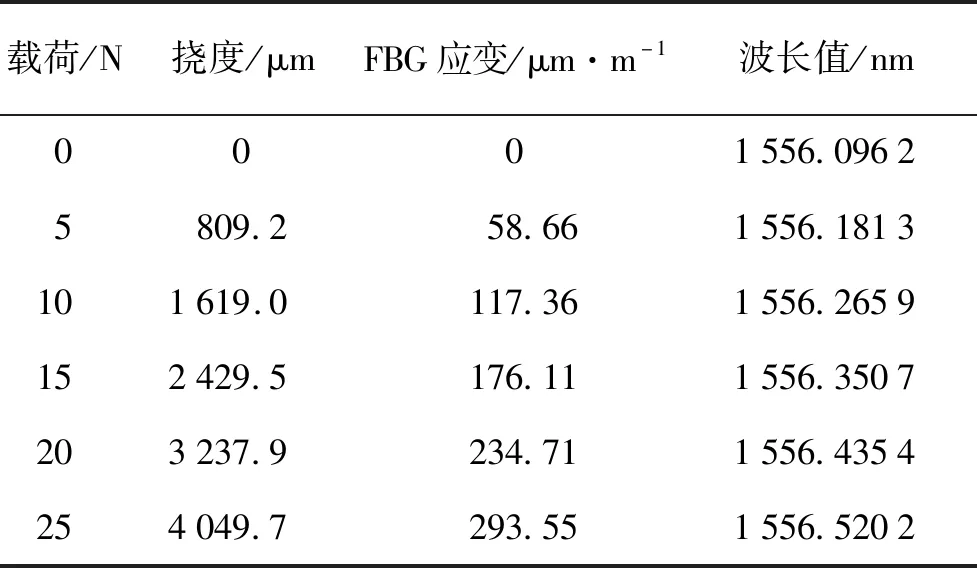
表6 FBG传感器应变测量结果Tab.6 Strain measurement results of FBG sensor
将FBG传感器测得的波长数据用最小二乘法对FBG传感器应变进行拟合,得到该FBG的应变灵敏度为1.442 pm/×10-6。
4.4 不确定度评定
4.4.1 测量模型及不确定度分量分析
提出针对FBG传感器在等强度悬臂梁上使用基于挠度法的应变标定模型,由式(6)、式(9)、式(11)可得测量模型为
(12)
分析认为测量不确定度分量主要有梁的表面应变εx、应变比例放大系数α、应变传递效率β、波长变化量Δλ等4项。
式(12)中,εx的相关不确定度分量包括梁的厚度、挠度待测点到固定端距离;α的相关不确定度分量包括梁与基片之间粘接胶的厚度、光纤下表面到基片的槽底的距离、光纤的半径、基片的厚度、基片上的槽深、梁的厚度等;β与被测传感器的安装方式等相关,例如,胶粘方式或焊接方式。其中胶粘方式则需考虑胶层厚度及材料等参数,甚至也包括应变传递过程及其机理,考虑标定与应用的状态一致,该项误差的不确定度主要是由被测传感器安装误差引入。如果是焊接方式,则β的取值范围可以接近于1,对于实验采用的FBG传感器,采用应变传递理论、有限元仿真及实验数据综合估算该实验得到β的不确定度约为U=0.1%,k=2,不同安装情形的FBG传感器应变传递效率β的不确定度可能会有较大差异。Δλ与解调仪解调得到的波长值有关。
4.4.2 不确定度的合成与扩展
具体不确定度的各个分量见表7。对式(12)各分量求偏导并计算。其中εx的相对合成标准不确定度满足式(13):
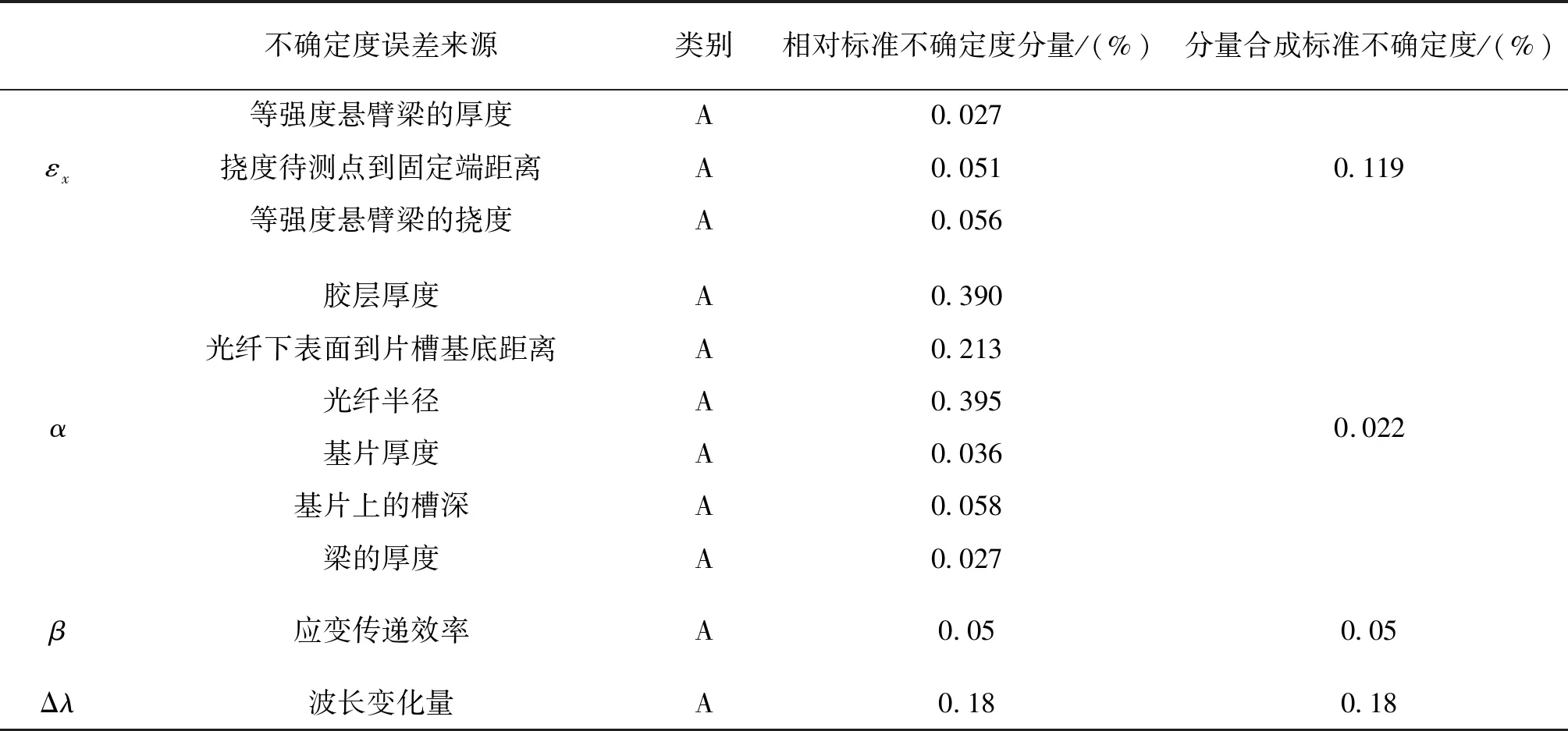
表7 标准不确定度一览表Tab.7 Standard uncertainty list
(13)
FBG传感器应变的相对扩展不确定度为:
=0.13%
(14)
根据式(12)计算FBG传感器的应变灵敏度Kε的相对不确定度为(k=2):
(15)
5 结 论
本文研究了基于挠度分析的FBG传感器在等强度悬臂梁上的的应变测量方法。通过对梁进行仿真,得到了不同载荷下的挠度和应变分布情况,验证了挠度测量方法的准确性。然后设计了挠度法的FBG传感器应变测量装置并进行了实验,对挠度法测量得到的梁的表面应变进行分析,反推出梁的弹性模量,并对梁的挠度、胶层厚度、标距等重要参数进行了精确的测量。使用以上测得的相关参数来进行建模和有限元仿真,结合计算分析得到FBG传感器的应变,最后对挠度法标定FBG传感器的结果进行了不确定度评定,取包含因子k=2,得到FBG传感器应变灵敏度的相对扩展不确定度<0.5%。该方法为高精度的FBG传感器应变测试的精度评定提供了技术支持。

