普朗克常数精密测量的历史和现状

李玉芬,和穗荣,韦联福, 2

(1. 西南交通大学信息科学与技术学院, 四川成都610031；2. 东华大学理学院,上海201620)

1 引 言

基本物理常数是物理学领域的一些普适常数。它们被假设在宇宙中任何地方和任何时刻都相同,这些常数的准确数值，与测量地点、时间及仪器、材料等无关。其中,6个比较常用的基本物理常数及其推荐值见表1所示[1]。

表1 基本物理常数及其推荐值Tab.1 Recommended values of basic physical constants

除了万有引力常数G外,其它5个基本物理常数均已被定义为精确值,特别是普朗克常数2019年被精确定义。事实上,该常数自1900年普朗克在研究黑体辐射规律引入以来,人们一直努力实现其精密测量，直到2017年,有超过3家机构提交的该常数测量值相对不确定度优于5×10-8,其中加拿大国家研究委员会(National Research Council,NRC)使用基布尔秤测得该常数的值[2]h=6.626 070 133(60)×10-34J·s,相对不确定度(9.1×10-9)优于2×10-8,才被国际度量衡委员会(International Committee of Weights and Measures,CIPM)批准推荐国际科技数据委员会(Committee on Data for Science and Technology,CODATA)2017年的平差结果为该常数的精确值[3]。

表2列出了历年CODATA对该常数的推荐值及其相对不确定度[4～6]。2019年5月20日CODATA将该常数的平差结果h=6.626 070 150(69)×10-34J·s (其相对不确定度为1.0×10-8)定义为普朗克常数的精确值。由此,国际单位制中7个基本单位: 电流单位安培A、热力学温度单位开尔文K、物质的量单位摩尔mol、时间单位秒s、长度单位米m、发光强度单位坎德拉cd和质量单位千克kg均实现了基本物理常数定义[7]。

表2 历年CODATA对普朗克常数的平差结果Tab.2 Adjustment results of Planck constant by CODATA

普朗克常数的精确测量之所以重要,是因为： 第一,作为量子理论的重要标志,它几乎与所有的量子效应的实验观测密切相关,其精确值涉及许多量子现象的描述；第二,由真空中的光速c、万有引力常数G和它所定义的普朗克长度lP=(ћG/c3)1/2和普朗克时间tP=(ћG/c5)1/2与早期宇宙大爆炸物理性质的研究密切相关(约化普朗克常数ћ=h/(2π)),普朗克常数和万有引力常数的精确测量对理解物质世界的起源特别重要；第三,普朗克常数的单位J·s可改写成kg·m2·s-1，在用光速精确定义长度单位“米”和用铯原子能级跃迁频率精确定义时间单位“秒”的情况下,普朗克常数的精确值因而可作为质量单位“千克”的物理基准,实现对1889年以来一直采用的国际千克原器(International prototype kilogram,IPK)作为千克单位实物标准的取代。

本文从测量方法方面，系统回顾普朗克常数精密测量的发展历史及现状。

2 普朗克常数的间接测量方法

2.1 黑体辐射谱测量法

普朗克于1900年发表了与黑体辐射谱实验结果完全相符的黑体辐射经验公式——普朗克公式,由此引入了普朗克常数。因此,黑体辐射谱的测量自然就成了普朗克常数测量的一个有效途径,见图1所示。

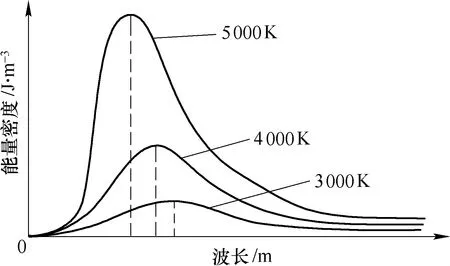
图1 不同温度下黑体辐射能量密度与波长的关系Fig.1 Relationship between energy density and wavelength of black body radiation at different temperatures

例如,在不同温度T1和T2下,可测得每秒辐射出的能量(即热量)分别为S1和S2,则由普朗克公式可得两者能量之差与总能量密度之比为：

(1)

式中：c为光速；kB为玻尔兹曼常数;ν为振子的振动频率。根据维恩位移定律可知,峰值波长与温度的乘积等于定值。因此,通过测量维恩位移常数β=0.002 94… m·K的值,能量最大的辐射波长λmax由式(2)确定:

(2)

式中：x=4.965 1…；T为热力学温度。由实验测得的最大辐射波长和黑体温度，普朗克本人推算出普朗克常数值为h=6.55×10-34J·s[8]。然而，该方法涉及的实验测量量较多，精度难以保证，在后来的普朗克常数精密测量中很少采用。

2.2 光学测量法

1888年Hertz发现了光电效应。1905年爱因斯坦[9]用普朗克的量子理论圆满地解释这一效应,提出了光电效应方程，成为后来许多实验测量普朗克常数的物理基础：

eU=hf-W

(3)

式中：U为光电流的截止电压，eU为光电子逸出阴极金属表面所具有的最大动能；f为光量子频率，hf为光量子能量；W为光电效应实验中所用光阴极材料的逸出功。通过测量不同频率入射光下的截止电压，然后计算U-f曲线的斜率，得到h/e的值，从而实现普朗克常数值的间接测量。很多普朗克常数实验测量(包括目前大多数大学物理实验课程中的普朗克常数测量实验)都是基于这一思想，或者将光阴极的光电效应换为原子电离效应以避开逸出功的测量。

2.2.1 外光电效应实验法

1914年密立根利用油滴实验首次测出了基本电荷的电荷量，证明了电荷的不连续性；继而在1916年率先验证了爱因斯坦光电效应方程的正确性，从而开创了实验间接测量普朗克常数h的先河。结合他本人所测得的e值，首次实现了相对不确定度为5×10-3的普朗克常数值h=6.57×10-34J·s的实验测量[10]。1928年,Lukirsky和Prilezaev[11]用与密立根类似的方法,用铝、锌、锡、镍、镉、铜和铂7种金属进行多次光电效应实验,测到的普朗克常数的平均值为h=6.543×10-34J·s,相对不确定度为1×10-3～2×10-3。然而,此方法光阴极材料的逸出功难以精确测定,光电流测量的不准确性等均会导致较大的实验误差；更重要的是,由于光阴极中的自由电子服从费米-狄拉克分布,在常温下热噪声导致光电流很强的暗计数,因而实验精度只能到10-3量级。现阶段的大学物理实验课程中普朗克常数测量实验,基本也都是跟据这一实验思路来进行设计的,只不过所用的光电管真空度更高、光电流测得更准,但精度基本上也还是在10-5量级及以下。

2.2.2 X射线法

X射线谱由连续谱和标识谱组成,电子作为一种高速带电质点,其打到靶子上发射的X射线与靶材无关,是连续谱。1915年哈佛大学Duane和Hunt在研究发现X射线连续谱具有短波长度限制,光电管阳极电压U与X射线的最高频率ν或最短波长λmin成反比,即满足“Duane-Hunt关系”：

(4)

1917年Duane和Blake[12]率先将Duane-Hunt关系用于测量普朗克常数的实验中,得到结果为h=6.555×10-34J·s。1921年中国学者叶企孙与Duane、Pzlmer[13]合作在哈佛大学杰斐逊物理实验室改进了之前的实验,重新测定,得到了相对不确定度约为1.4×10-3的普朗克常数值为h=(6.556±0.009)×10-34J·s。该结果是利用X射线连续谱测量普朗克常数的实验中相对不确定度最优的一个,1926年被著名基本物理常量评定人Birge收集在基本物理常数数据表中[14],作为普朗克常数的标注值使用了很多年,是中国学者在物理学早期研究的最主要贡献之一。但该方法有着明显的局限性,X射线连续谱短波限法测量普朗克常数的关键在于λmin的精确测定,然而分光计分辨率的限制使得谱线不可避免地展宽,边界模糊；另外,靶材厚度、光缝与靶材的距离,以及后来发现边界光谱的不规则性等许多因素都使得测量结果难以进一步提高。

作为改进的方法之一,Bearden 和Schwarz 发明了测量普朗克常数的X射线原子游离法[15],并依次研究了Cu、Ga、Ni和Zn原子的K层电子和W的L层电子的发射情况,通过式(5)得到h/e的测量结果。

(5)

式中：eUe为X射线正好可以使原子钟电子逸出时的能量；λe为X射线能量被吸收后的光谱边界波长。最初用此方法得到的相对不确定度为1×10-4，后来(1955年)Bearden应用于对硅晶格参数进行测量，得到h=6.251 7(23)×10-34J·s，相对不确定度为2×10-5。

2.2.3 康普顿散射法

康普顿效应表明，单色光与静止电子发生碰撞后，波长会产生Δλ的变化。因此，测量Δλ以及该入射光线与散射光线的夹角φ，通过式(6)可以得到h/(mc)，m为电子质量,从而实现普朗克常数的间接测量。

(6)

由于电子能量远比X光光子能量小,所以电子可看作处于静止的理想状态[16]。实际上电子在原子中有任意方向上的运动速度,因而夹角会有一定的展宽,从而增大测量的相对不确定度。此方法所测结果的相对不确定度只有2×10-3。

与康普顿效应不同,1949年DuMond等[17]利用一对电子和正电子在静止状态下所发生湮没效应,释放的能量E为

E=2mc2

(7)

理想情况下，能量E被2个光子平均吸收，且光子背向运动情况下，通过测量所产生的光子波长：

(8)

实现了相对不确定度约为1×10-4的普朗克常数测量。

2.3 电学测量法

2.3.1 约瑟夫森效应测量法

1962年,英国剑桥大学的Josephson预言,2个超导体被1个薄的绝缘体隔开时将会出现库珀对的隧穿效应[19]；1963年Anderson等[20]实验证实该预言。这里,2块超导体弱耦合呈现超导—绝缘—超导(S-I-S,约瑟夫森结)结构,在2个超导体上加直流电压,电子能无阻碍地穿过绝缘层,从而出现隧穿电流。这是一个交变的振荡超电流,振荡的频率f与电压U关系有：

(9)

频率f被称为约瑟夫森频率。这就是交流约瑟夫森效应，被用于定义电压自然基准。

1963年Shapiro首先观测到,在约瑟夫森结上辐射频率为f的微波时结的两端会形成电压台阶,见图2。这里，电压UJ在数值上是量子化的[21]：

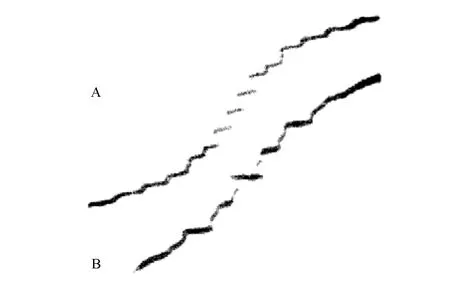
图2 约瑟夫森结电压台阶[21]Fig.2 Voltage steps of Josephson junction[21]

(10)

式中n为不同台阶数。由此可以定义约瑟夫森常数KJ=2e/h。1973年,约瑟夫森常数列入基本物理常数国际推荐表中[22],其精度水平为1×10-6。1988年,CIPM通过决议,建议从1990年1月1日起,在世界范围内采用约瑟夫森电压取代电压实物基准(标准电池组)为自然基准,将约瑟夫森常数KJ-90=2e/h=483 597.9 GHz/V定为无误差的国际公认值[23]。但是,受到电子电荷量测量精度的影响,由此确定的普朗克常数值为h=6.626 176(36)×10-34J·s,其平差的相对不确定度仅为5.4×10-6。

2.3.2 量子霍尔效应测量法

1879年,Hall在研究金属导电机制时发现一种电磁效应：将1个矩形截面的导体放入匀强磁场中,当导体内电流方向垂直于磁场方向时,载流子发生偏转,导体在与电流和磁场都垂直的方向上的两端会产生电势差,这个现象就叫做霍尔效应。利用欧姆定律可知：

(11)

1980年,冯·克利青等[24]在1.5 K低温、18 T强磁场环境下的金属—氧化物—半导体场效应晶体管(MOSFET)实验中发现量子霍尔效应,即电阻与磁场强度不呈线性关系,而是一种量子化的阶梯型关系,如图3所示。

图3 霍尔电阻台阶与实验所用MOSFET管[24]Fig.3 Hall resistance steps and MOSFET used in experiment[24]

量子化的电阻RH可表示为：

(12)

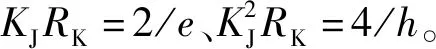
3 力学平衡法直接测量普朗克常数

不同于上述通过测量普朗克常数和电子电荷比值，来实现普朗克常数间接测量的光学和电学方法，利用以测力天平为代表的力学平衡法，可以直接测量普朗克常数。通过区分电感电磁力和电容电磁力,测力天平分为电流天平和电压天平两种,基本原理都是建立一对平衡力,利用质量单位复现电流或电压单位，从而实现普朗克常数的直接测量。

3.1 电流天平

为了复现电流单位安培而设计的电流天平是最早的力学天平,它在力学与电磁学量之间建立了关系。利用砝码重力与通电线圈的磁力平衡,实现机械能量与电磁能量的等价,从而达到复现电流单位的目的。电流天平可分为瑞利型和艾顿型两种类型[27],结构分别如图4(a)、图4(b)所示。

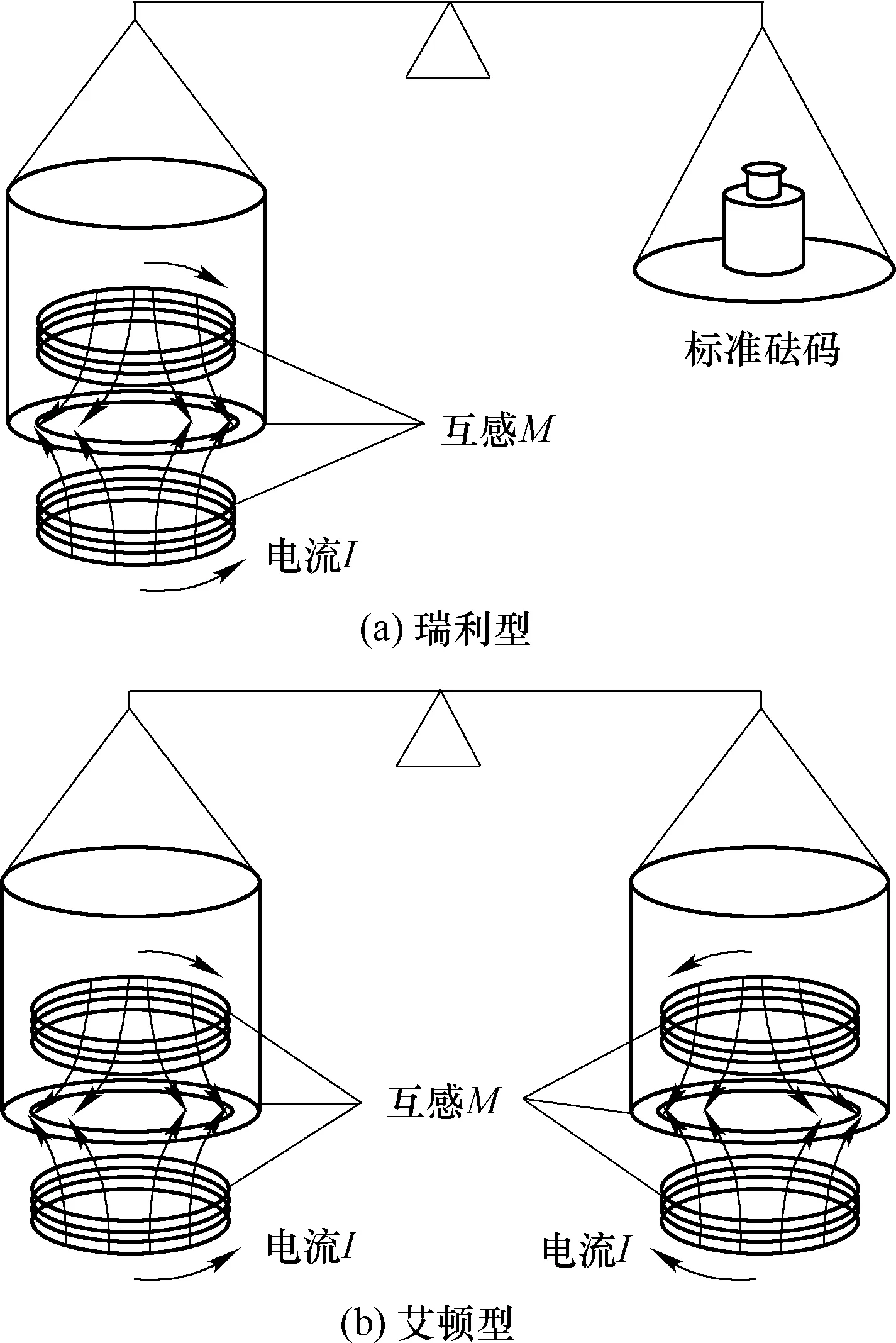
图4 电流天平结构示意图[27]Fig.4 Structure diagrams of current balances[27]

瑞利型电流天平安培单位复现表达式为：

(13)

式中：mg为标准砝码的重量；∂M/∂z表示互感M沿z方向上的力,根据线圈相关参数计算可得到。由于几何因子∂M/∂z的精确测量水平有限,安培复现的相对不确定度只能达到1×10-6水平。不过,电流天平方案的主要优点是实现过程简单,只需要一对平衡力就可以实现。

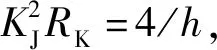
(14)

这一方法测量普朗克常数的精度水平受到电流天平复现电流单位的相对不确定度影响,实际上并不常用。但是,这却是最早把普朗克常数h和质量m联系起来的方案,是功率天平和能量天平的初始版本。

3.2 电压天平

电压天平的原理是借助天平两端双板电容器C两板之间的静电力与重力为mg的物体平衡，得到电压U：

(15)

式中∂C/∂z是垂直电容器两板方向上的电容梯度。与电流天平以相同的方式引入普朗克常数，可得到方程：

(16)

电压天平主要有3种[28]：开尔文型、能量变化法和液体静电计,实现方法见图5所示。

图5 电压天平不同实现方法[28]Fig.5 Different realization methods of voltage balances[28]

利用电压天平,澳大利亚联邦科学与工业研究组织(Commonwealth Scientific and Industrial Research Organisation, CSIRO)测得的普朗克常数为h=6.626 068 4(36)×10-34J·s,相对不确定度为5.4×10-7；德国联邦物理技术研究院(Physikalisch Technische Bundesanstalt,PTB)的Funck和Sienknecht用电容器电压天平测得普朗克常数为h=6.626 067 0(42)×10-34J·s[29],相对不确定度为6.3×10-7。

电压天平测量普朗克常数方案的主要难点是：实验所需的电压较高(高达100 kV),而且机械加工工艺不足会引起电容变化,从而限制此方法测量普朗克常数的不确定度无法优于1×10-7。

3.3 功率天平(基布尔秤)测量法

功率天平方案也被叫做瓦特天平(Watt balance),起源于电流天平,最早在1975由英国国家物理研究所(National Physical Laboratory,NPL) Bryan Kibble 提出[30],后来被称为基布尔秤(Kibble balance)。通过约瑟夫森效应和量子霍尔效应,基布尔秤将宏观世界的质量与微观世界的普朗克常数联系了起来。基布尔秤可分为称重模式和速度模式两种模式[31]。

1)称重模式[32]

其结构与加入磁场的电流天平相似,原理见图6所示。基布尔秤方案测力模式建立的平衡关系式为：

图6 基布尔秤方案称重模式原理示意图[32]Fig.6 Schematic diagram of weighing mode of Kibble balance[32]

BLI=mg

(17)

式中：B是线圈所处的磁场；L是线圈的有效长度；I是流过线圈的电流。称重模式主要难点和缺点是磁场B和线圈长度L的精确测量,后面Kibble对其进行改进,引入线圈速度,克服了称重模式的不足。

2)速度模式[32]

去掉机械力一侧悬挂的物体,将线圈设置为开路,线圈以恒定的速度在磁场中做切割磁感线运动,见图7所示。

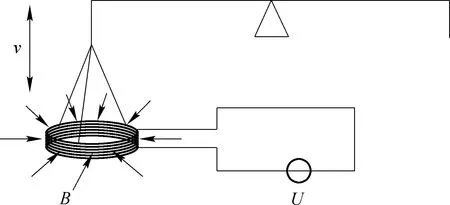
图7 基布尔秤方案速度模式原理示意图[32]Fig.7 Schematic diagram of speed measurement mode of Kibble balance scheme

基布尔秤方案速度模式依据法拉第电磁感性定律,可得到感应电压ε：

BLv=ε

(18)

将式(17)与式(18)联立消去BL可得到：

εI=mgv

(19)

这克服了需精密测量几何因子B、L的难题,不过同时也引入了准确测量瞬时速度和感应电压的难题。显然,等式左边是电功率,右边是机械功率,等式联系的是一个功率的平衡,所以这个方案也被叫做“功率(瓦特)天平”。

从原理图可以看出,实际上等式中电流并不是直接测量得到,而是通过测量采样电阻R上的电压降U得到,所以实际计算公式为：

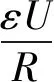
(20)

因为电压可以使用约瑟夫森电压标准,电阻可以使用量子霍尔电阻,所以使用基布尔秤可以实现普朗克常数的测量：

(21)

式中：R=h/(ie2)；U=nhfU/(2e)；ε=nhfε/(2e)；i和n都是正整数；fU和fε分别是电压U和ε的约瑟夫森频率。

基布尔称具有联系宏观物体质量与普朗克常数,且相对不确定度小的优点,成为近年来实现用普朗克常数定义质量单位千克的主流方法,使用基布尔秤方案测量h的进展如表3所示。尤其是,2017年NRC使用基布尔秤测得的值h=6.626 070 133(60)×10-34J·s,其最小相对不确定度达到了 9.1×10-9,是目前精度最高的测量结果,该值在2017年被CODATA收录用于普朗克常数的平差,为2019年5月20日定义普朗克常数为精确值做出重大贡献。

表3 1967～2017年使用基布尔秤测量的进展Tab.3 Progress in measurement of h with Kibble Balance from 1967 to 2017

3.4 能量天平测量法

2006年,中国计量科学研究院(National Institute of Metrology,NIM) 张钟华团队提出了一个测量普朗克常数的新方案,称为能量天平。它同样有两个模式,与基布尔秤的不同之处在于,能量天平对称重模式进行了修改,并用互感测量模式取代速度模式[33],成功避开了基布尔秤方案动态测量的难点。

图8为能量天平方案称重模式的原理示意图,平衡关系可以表示为[34]：

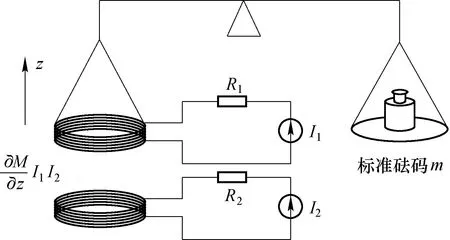
图8 能量天平方案称重模式的原理图[32]Fig.8 Schematic diagram of weighing mode of energy balance[32]

(22)

式中：Δfz是天平在平衡过程中非常小的残余力，即砝码重力与电磁力平衡后的差值；M是两线圈之间的互感；∂M/∂z难以直接测量，所以等式两边同时引入z方向上从z1到z2的积分：

mg(z2-z1)=[M(z2)-M(z1)]I1I2+

(23)

当磁场在z方向上是匀强磁场时，式(23)中的积分项就会变得很小，所以只需要知道2个互感值M(z2)、M(z1)和距离z1-z2，即可得到质量m的值，动态误差被消除。显然，这个天平实现的是机械能量差与电磁能量差的平衡，所以得名为能量天平。基于此，普朗克常数h就可以通过

(24)

来测定。互感测量模式原理如图9所示[37]。

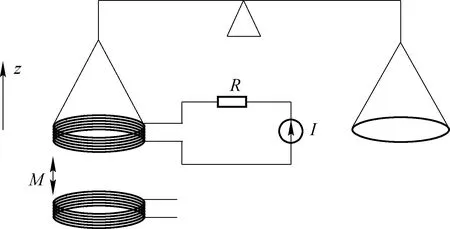
图9 能量天平互感测量模式[37]Fig.9 Schematic diagram of mutual inductance mode of Energy Balance scheme[37]

去掉右侧的砝码,天平稳定后,测量左侧悬挂线圈(上)在垂直方向上2个不同位置z1和z2处与激励线圈(下)的互感值,所以能量天平的两个模式都是静态模式,由此克服了基布尔秤方案动态测量的难点,不过能量天平方案仍面临一些难题：互感值的测量精度水平较低、大电流满足磁力要求的同时使线圈系统严重发热等。

从2001年开始到2011年原理验证装置成功研制,2013年NIM-1样机装置实现了相对不确定度达到8.9×10-6的普朗克常数测量,改进后相对不确定度达到2.6×10-6[35],验证了能量天平测量的可行性。2017年5月NIM-2装置实现了h=6.626 069 2×10-34J·s、相对不确定度为2.4×10-7的普朗克常数测量[36],精度达到了国际先进水平。进一步的改进研究[37～40],预计相对不确定度可达到5×10-8,甚至更小,从而有望用于独立复现质量千克,建立我国自己的质量计量的物理基准。

4 结论和展望

自黑体辐射公式引入普朗克常数以来，普朗克常数就成为物理学中极为重要的基本物理常数。一方面它是量子世界的基本特征(当h=0时物理现象满足拉普拉斯决定论)，与几乎所有的量子效应有关，也与物理学中质量定义的物理基准直接相关；另一方面，在长度小于普朗克长度、时间短于普朗克时间的尺度下，时间和空间标度没有意义。因此普朗克常数的精密测量对物理学基本理论研究和高精度测量技术的研发均有着重要的意义。

普朗克常数的精密测量经历了近120年的历史。到2019年，以认定 2017年CODATA对普朗克常数的平差值h=6.626 070 150 (69 )×10-34J·s(相对不确定度为1×10-8)的精确值为标志，普朗克常数的精密测量取得了里程碑式成果。

尽管如此，在更高精度上实现普朗克常数的测量仍然具有重要意义。 普朗克常数测量一般是通过h/e的间接测量得到h的值,精度受电子电量e测量精度的影响。目前e的精度水平也只有10-9,所以规避e从而进一步提高普朗克常数测量精度是一个值得探索的方向。