不同方法评定标准溶液稀释不确定度对仪器校准结果的影响及分析

孙喜荣，黄金梅

(陕西省计量科学研究院，陕西西安710065)

1 引 言

化学分析仪器校准时，经常需要将高浓度有证标准物质稀释到计量技术规范规定的浓度点才可以使用。稀释过程中引入的不确定度分量是校准结果不确定度的重要来源之一。目前，评定溶液稀释结果不确定度方法有两种[1,2]:一种是按照JJF 1059.1—2012《测量不确定度评定与表示》规定，采用GUM法，对数学模型中的各分量，用数学方法求出各分量灵敏系数及标准不确定度后，进行合成，得到结果的扩展不确定度，可称为数学方法[3～7]；另一种是根据经验，求出数学模型中各分量的相对标准不确定度后，进行合成，得到结果的扩展不确定度，可称为经验方法[8～14]。目前，经验方法使用较为普遍。本文以校准一台红外分光测油仪[15]为例，将1 000 mg/L高浓度有证标准物质(标准原液)稀释为目标浓度为10 mg/L和50 mg/L的校准用标准溶液，分别用上述两种方法对稀释结果进行不确定度评定，比较分析两种评定方法及其结果的异同，以及对最终校准结果的影响。

2 标准溶液稀释方法

标准物质原液：红外测油仪用标准物质，GBW(E)130171，1 000 mg/L，Urel=3%(k=2)，中国计量科学研究院研制。

目标浓度10 mg/L标准溶液：用1 mL单标线吸量管，吸取标准物质原液1 mL至100 mL容量瓶并稀释至刻度。

目标浓度50 mg/L标准溶液：用5 mL单标线吸量管，吸取标准原液5 mL至100 mL容量瓶并稀释至刻度。

3 数学模型

标准溶液稀释数学模型为：

式中：C1为标准物质原液浓度，mg/L；C2为目标标准溶液浓度，mg/L；V1为移取标准物质原液体积，mL；V2为配制标准溶液体积，mL。

4 数学方法评定不确定度分析

4.1 10 mg/L标准溶液

4.1.1 灵敏系数

4.1.2 不确定度分量的主要来源

(1) 标准物质引起的标准不确定度u(C1)

查证书得红外测油仪用标准物质的不确定度为3%，k=2，则

(2)1 mL单标线吸量管的标准不确定度u(V1)

常用玻璃量器检定规程(JJG 196—2006)规定A级1 mL单标线吸量管的最大允差为±0.007 mL，按均匀分布，吸取1 mL原液时的标准不确定度为：

(3)100 mL容量瓶的标准不确定度u(V2):

常用玻璃量器检定规程(JJG 196—2006)规定A级100 mL容量瓶的最大允差为±0.10 mL，按均匀分布，则

4.1.3 合成标准不确定度uc

=0.150 mg/L

4.1.4 扩展不确定度

取k=2，则

U=2×uc=0.30 mg/L

4.2 50 mg/L标准溶液

4.2.1 灵敏系数

4.2.2 不确定度分量的主要来源

(1) 标准物质引起的标准不确定度u(C1)

同第4.1.2节

u(C1)=15 mg/L

(2) 5 mL单标线吸量管的标准不确定度u(V1)

常用玻璃量器检定规程(JJG 196—2006)规定A级5 mL单标线吸量管的最大允差为±0.015 mL，按均匀分布，量取5 mL溶液时的标准不确定度为

(3) 100 mL容量瓶的标准不确定度u(V2)

同第4.1.2节

u(V2)=0.057 7 mL

4.2.3 合成标准不确定度uc

=0.750 mg/L

4.2.4 扩展不确定度

取k=2，则

U=2×uc=1.5 mg/L

5 经验方法评定不确定度分析

5.1 10 mg/L标准溶液

5.1.1 不确定度分量的主要来源

(1) 标准物质引起的相对标准不确定度urel(C1)

查证书得红外测油仪用标准物质的不确定度为3%，k=2，则

(2) 1 mL单标线吸量管的相对标准不确定度urel(V1)

根据第4.1.2节所述，吸取1 mL原液时的相对标准不确定度为

(3) 100 mL容量瓶的相对标准不确定度urel(V2)

根据第4.1.2节所述，可得

5.1.2 合成相对标准不确定度uc，rel

5.1.3 扩展不确定度

取k=2，则

Urel=2×uc，rel=3.10%

5.2 50 mg/L标准溶液

5.2.1 不确定度分量的主要来源

(1) 标准物质引入的相对标准不确定度urel(C1)

同第5.1.1节

(2) 5 mL单标线吸量管引入的相对标准不确定度urel(V1)

根据第4.2.2节所述，量取5 mL溶液时的相对标准不确定度为：

(3) 100 mL容量瓶的相对标准不确定度urel(V2)

同第5.1.1节

5.2.2 合成相对标准不确定度uc，rel

5.2.3 扩展不确定度

取k=2，则

Urel=2×uc,rel=3.02%

6 标准溶液稀释不确定度评定结果

数学方法评定标准溶液稀释不确定度结果见表1，经验方法评定标准溶液稀释不确定度结果见表2。

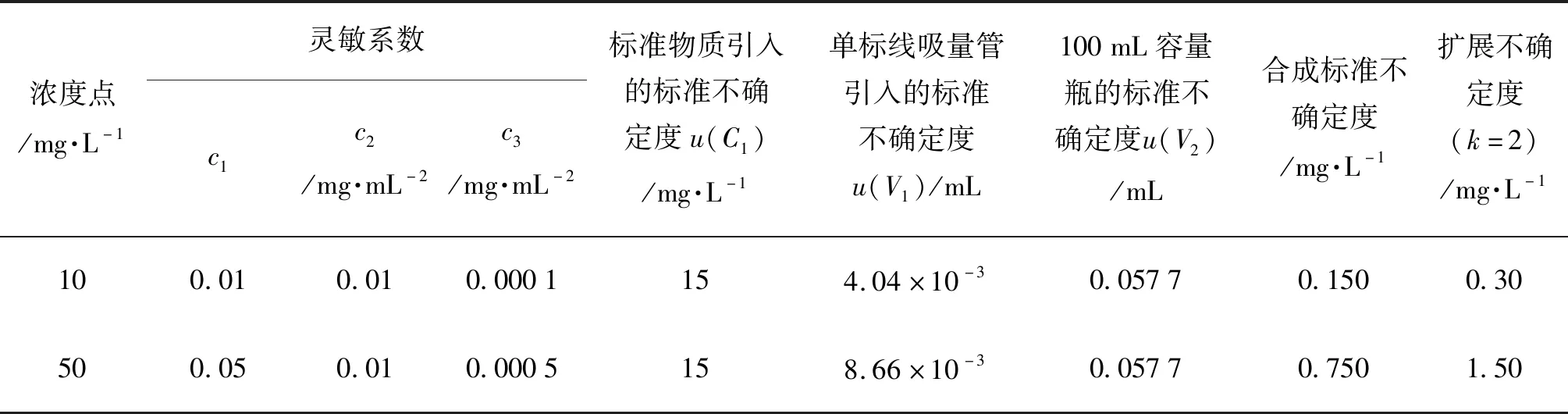
表1 数学方法评定标准溶液稀释不确定度结果Tab.1 Mathematical methods for evaluation of uncertainty of the diluted standard solution results

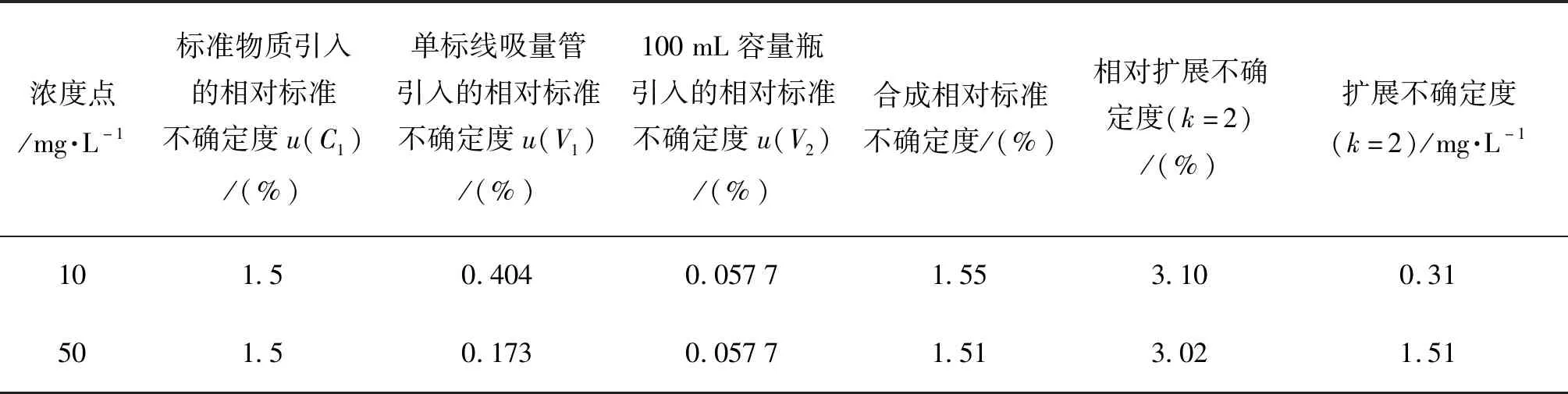
表2 经验方法评定标准溶液稀释不确定度结果Tab.2 Empirical methods for evaluation of uncertainty of the diluted standard solution results

由表1和表2可见，评定方法不同，结果有所不同。数学方法理论依据充分，计算结果准确，因此，在需要精确评定结果不确定时，最好选择JJF 1059.1—2012《测量不确定度评定与表示》中规定的数学方法。经验方法计算简便，不需要将灵敏系数代入计算，在不确定度评定结果准确性要求不高时，可选择使用。

7 仪器校准结果不确定度评定分析

依据JJG 950—2012《水中油份浓度分析仪》，对一台北京华夏科创仪器技术有限公司生产的红外分光测油仪(型号OIL 480)在10、50 mg/L浓度点进行连续3次重复测量，取其平均值作为仪器测量值，分别用式(1)、式(2)计算示值误差。

测量范围≤10 mg/L时，

(1)

测量范围>10 mg/L时，

(2)

式中：Δρrel为测量值大于10 mg/L时的示值误差。

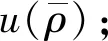
表3 仪器测量重复性数据Tab.3 Repeatability of measurement data

由表4可见，仪器示值误差不确定度评定中，在重复性引入的标准不确定度相同时，标准物质稀释的不确定度直接影响仪器示值误差校准结果的不确定度。两种方法评定不确定度的相对误差在3.85%以内，当不需要对校准结果进行准确评定时，可任选一种方法。

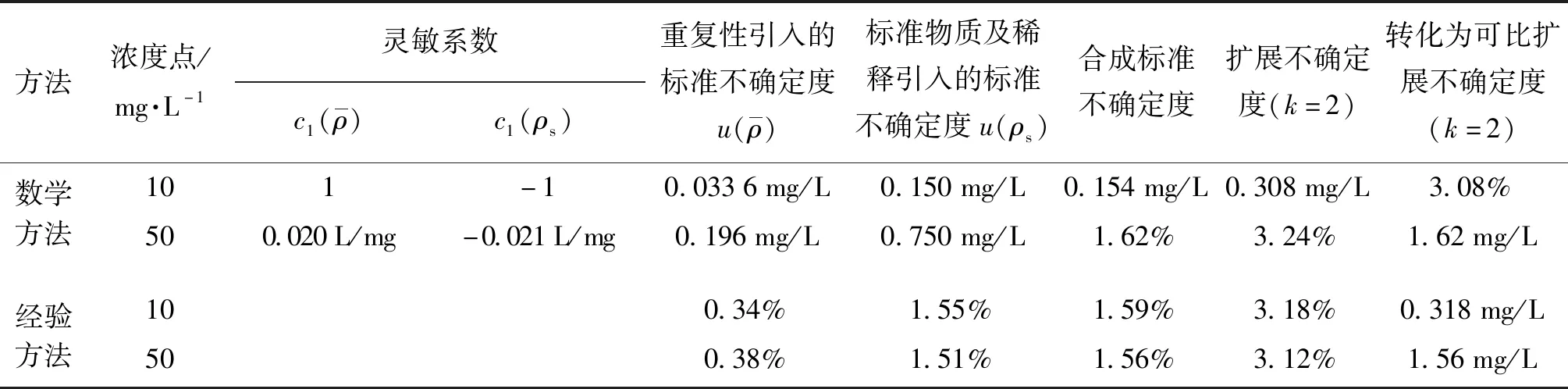
表4 两种方法评定仪器示值误差校准结果不确定度比较Tab.4 Two methods for evaluation of uncertainty about indication error of calibration results

8 结 论

本文以红外测油仪校准用标准物质稀释为例，分别用数学方法和经验方法对将标准物质原液(浓度1 000 mg/L)稀释成10、50 mg/L校准用标准溶液的不确定度进行了评定，接着对仪器的校准结果进行了不确定度评定，结果发现两种方法的评定结果不尽相同。标准物质稀释结果的不确定度直接影响仪器示值误差校准结果的不确定度。笔者建议，在不确定度的评定中，若需要精确评定仪器校准结果的不确定度时，应选择依据JJF 1059.1—2012《测量不确定度评定与表示》中规定，对测量模型中的各分量用数学方法求出其灵敏系数及标准不确定度后进行合成，即数学方法进行评定。对于准确性要求不高情况，可以采用计算相对简单的经验方法。总体来看，二者结果差异不是很大。