非凸不可分离问题的广义交替方向乘子法的收敛性
薛中会, 胡惠晴, 党亚峥
(1.上海出版印刷高等专科学校,上海 200093;2.上海理工大学 管理学院,上海 200093)
1 问题的提出
考虑具有非凸不可分离的优化问题

式中:f:Rn→R∪{+∞}是恰当的下半连续函数;h:Rm→R是连续可微函数;g:Rn×Rm→R是光滑函数,且x和y是不可分离的。
问题(1)的一个特殊形式是没有函数g,且目标函数是可分离的,即
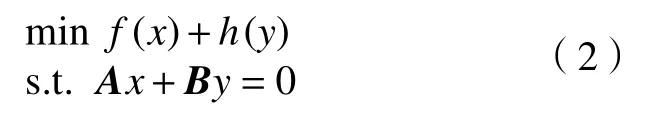
利用交替方向乘子法(ADMM)求解问题(2)的一种有效算法的迭代格式为
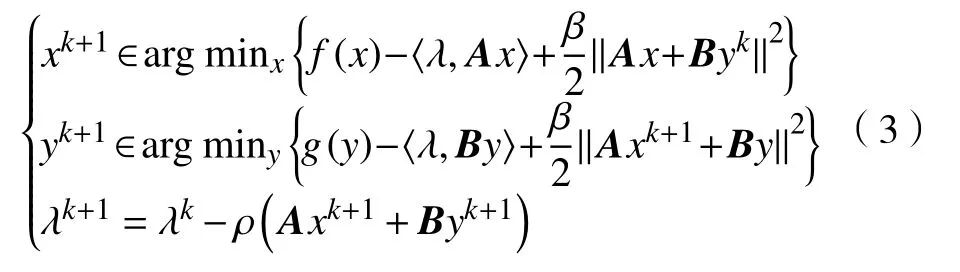
式中: λ为拉格朗日乘子; β为惩罚参数, β >0。
ADMM算法通过引入一个新的辅助变量,将原问题改写为一个目标函数可分离且辅助变量与原变量是线性约束的形式,通过交替更新原变量、辅助变量和对偶变量来迭代求解问题的最优解。通过引入合适的辅助变量,每个迭代步骤可以变成非常简单的子问题,通常可以收敛到稳定点或者被并行求解。这使得ADMM算法适用于求解大规模的优化问题。
对于f和h都是凸函数的情况,ADMM(式(3))的收敛性得到了很好的证明,并且对其进行了收敛率分析[1-3]。在没有凸性的假设下,更难以证明ADMM的收敛性。在这方面的研究取得了一些进展[4-8]。Guo等[4]利用经典ADMM算法求解非凸多块可分离最优化问题,证明了其收敛性,并且提出了一些充分条件,保证了算法的超线性和线性收敛速率。Li等[5]提出了一种近似ADMM算法来解决非凸非光滑优化问题,证明了当罚参数足够大且生成的序列有聚点时,算法所产生迭代点列收敛到稳定点。
目前的研究大多数考虑如下的问题:

然而,由于函数g的存在,即使目标函数是凸的情况,对ADMM(式(4))的收敛性分析的研究还处于初期,研究成果很少。并且由于约束条件中矩阵B的存在,使得收敛性分析变得更加困难。
Gao等[9]考虑了函数g是光滑函数以及函数f,h是凸函数的情况。通过假设 ∇g是利普希茨连续以及h强凸,证明了由ADMM算法生成的序列收敛到问题(4)的最优解。Chen等[10]在耦合函数g是二次函数的情况下,分析了ADMM解决问题(4)的收敛性。Liu等[11]提出了线性化ADMM来解决非凸非光滑的目标问题,通过将目标中的可微项以及增广项线性化,证明了算法的收敛性,然后将问题推广到多块并行的ADMM算法中。以上研究都是矩阵B为单位阵的情况。在耦合函数缺失的情况下,Wang等[12]研究了用Bregman距离修饰ADMM算法(BADMM算法),分别分析了矩阵B单射和非单射情况下算法的收敛性,证明了BADMM算法生成的序列收敛到稳定点。Guo等[13]提出了一种广义的ADMM算法来求解问题(4)。
本文研究广义ADMM算法的收敛性,通过假设矩阵B列满秩以及增广拉格朗日函数满足K-L不等式,当罚参数足够大时,证明了算法产生的序列收敛到其稳定点,从而证明了算法的收敛性。
2 预备知识
现给出理论分析所需要的概念和性质。
对于任意x∈Rn是函数f的极小值点的必要条件是 0 ∈∂f(x),满足这个条件的点称为稳定点,函数f的稳定点集记作 cr itf。
定义1令f:Rn→R∪{+∞}为正常的下半连续函数。
a.Fréchet次微分。
函数f在x∈domf的Fréchet次微分,定义为满足下列关系x∗∈ Rn的集合:
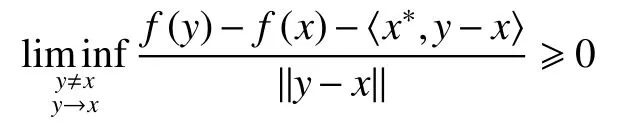
b.极限次微分。
函数f在x∈domf的极限次微分,定义为
∂f(x):={x∗∈Rn:∃xn→x,f(xn)→f(x),x∗n∈∂ˆf(xn),x∗n→x∗},记作∂f(x)。
c.若在函数f的定义域中满足 0 ∈ ∂f(x∗),则称x∗为f的稳定解。
d.对 ∀x,y∈domf,若满足∥f(x)−f(y)∥≤L∥x−y∥,则称f满足Lipschitz连续条件,L为Lipschitz常数。
引理1h:Rm→R是连续可微函数,且 ∇h是关于常数L利普希茨连续的,那么,对于任意的x,y∈Rn,有
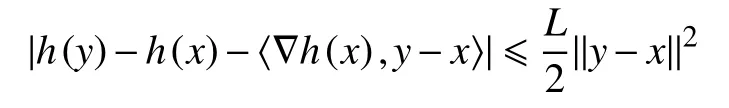
引理2(K−L不等式)设函数f:Rn→R∪{+∞}是恰当下半连续函数,对于 − ∞<η1<η2<+∞,令

若存在 η ∈(0,+∞],x∗的领域U以及一个连续的凹函数 φ : [0,η)→R+,满足如下条件:
a.φ( 0 )=0;
b.φ在 (0 ,η)连续可微且在0处连续;
c.φ′(s)>0,∀s∈ (0,η);[]
d.对 所 有 的x∈U∩f(x∗) 成立,则称函数f在x∗∈dom∂f上满足K−L性质。 引理3(一致K−L性质) Ω 是紧集,设函数f:Rn→R∪{+∞}是恰当下半连续函数。假设f在Ω上是常数并且在Ω 上的每个点满足K−L性质,那么,存在 ε >0,η>0以及 φ ∈ Φη,使得对于任意的x˜∈ Ω以及x∈{x∈Rn:d(x,Ω)<ε}∩{f(x˜) 针对问题(1),本文提出了一种广义交替方向乘子法(GADMM),即 其中, α ∈(0,2)是一个松弛因子,显然,当α=1时,GADMM即退化成经典的ADMM算法,并且当g≡0时退化成经典的GADMM算法。 在证明收敛性之前,先给出式(5)的变形,由最优性条件得到 利用式(6)的最后一个等式,得到 假设:令f:Rn→R∪{+∞}是弱凸函数,常数ω>0;h:Rm→R是连续可微函数,它的梯度 ∇h是利普希茨连续的,其利普希茨常数L1>0;g:Rn×Rm→R是光滑函数。问题(1)满足下列条件: a.矩阵B是列满秩的,且 Im (A)⊂Im(B); c.∇g在Rn×Rm的有界子集上是利普希茨连续的,即对于每个有界子集B1×B2⊆Rn×Rm,存在M>0,使得对于所有的(xi,yi)∈B1×B2,i=1,2,∥∇xH(x1,y1)−∇xH(x2,y2),∇yH(x1,y1)−∇yH(x2,y2)∥≤M∥(x1−y1,x2−y2)∥ e.存在L2,L3>0,使得 式中: α ∈(0,2)为松弛因子。()() 在收敛分析中,记ωk:=xk,yk,zk及vk:=xk,yk。问题(1)的增广拉格朗日函数为 式中: γ是与线性约束相关的拉格朗日乘子; β是惩罚参数, β >0。 此外,设 引理4在上述假设条件下,对于任意的l>k,有 式中, λBTB是BTB的最小的特征值。 证明由式(4)的第3项,以及假设的a,对于2个整数l>k,有 γl−γk∈ Im(B)。 由于B∈ Rn×q是列满秩的,因此,存在P∈ Rq×q,Q∈Rq×n,且(矩阵)P可逆,QQT=In×(n,)BT=PQ。由Im(B)=ImQT,可得γl−γk∈ ImQT,∥γl−γk∥2=由此得到 式中, λPTP是PTP的最小的特征值。 由矩阵P和Q的 定义,有 λBTB=λPPT,又因为线性代数的常见结论 λPTP=λPPT,因此,λPTP=λBTB。{()} 引理5令xk,yk,γk由算法GADMM式(式(5))产生,则有 证明首先将增广拉格朗日函数的差分拆分,得到 根据定义,有 因为,f是关于常数 ω的弱凸函数,因此,由式(7)的第1个关系式得到 根据假设的d,有 将上述3个不等式代入式(10),可得 类似地, 其中,最后1个等式由 得到。通过 ∇h的利普希茨连续性,由引理1及式(7)的第2个不等式,可得 又由于B是列满秩的,可得 将上述3个等式相加并代入式(12),可得 现计算式(9)剩余的项。 事实上, 且 将式(14)和式(15)相加,可得 根据引理4可得 其中,第2个不等式是由 ∇h的利普希茨连续性和假设的c得到。因此, 将式(17)代入式(16),得到 因此,将式(11),(13),(18)代入式(9),得到 其中,第2个不等式由假设的e得到,在最后1个等式中,令 由假设的c可知, δ >0。 引理6令序列由算法GADMM生成,且假设有界,因此,有 证明由于序列是有界的,则存在收敛子列且。由h和g的 连续性和f的下半连续性可知是下半连续的,从而可得 由 δ >0可得 因此, 此外,由式(17)和式(20)可得 因此, 引理7存在 ξ >0,使得 证明根据增广拉格朗日函数的定义,可得 进一步结合式式(7),可得 令 又由假设的c可得 根据式(17)可得 因此,由式(24)~(26)可得 令 由上式可以得到式(21)。 引理8假设序列为算法生成的有界序列,其所(有)极限点记为Sω0,则(()) a.Sω0是一个非空紧集,并且dωk,Sω0→ 0,k→+∞; 证明a.由Sω0的定义可直接得到。 b.对于任意点 (x∗,y∗,γ∗)∈S(ω0),存在子列 根据增广拉格朗日函数的定义,式(5)的x子问题等价于 即xk+1是关于变量x的全局最小点,由此可得 又因为Lβ(·)关于y和 γ连续,则有 由函数Lβ(·)的下半连续性可得 因此,结合式(27)和式(28),可得 由此可以推断 定理1若Lβ(·)满足K−L性质,则+∞,且序列收敛到Lβ(·)的一个稳定点。 证明由引理8可知,因此,考虑以下2种情况: a.存在整数k0使得由引理5可知, 因此,对任意的k>k0,有vk+1=vk,结合式(16)可知,对于任意的k>k0+1,有 ωk+1=ωk成立。 b.假设对于任意的k都有成立,存在使得对于所有的,有 其中, 由于 结合引理5,可得式(30)成立,且由式(30)可得 进一步,将上式从k˜ +1到m求和,得到 进一步由式(17)可得 此外,由于 因此, 研究了非凸不可分离的线性约束优化问题,以及求解该问题的广义交替方向乘子法(GADMM),在矩阵B不是单位阵的情况下,要求其列满秩,通过假设增广拉格朗日函数满足K-L不等式,证明了当惩罚参数大于一定的阈值时,算法生成的序列收敛到增广拉格朗日函数的稳定点。
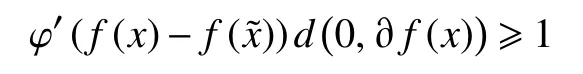
3 算法及收敛性分析






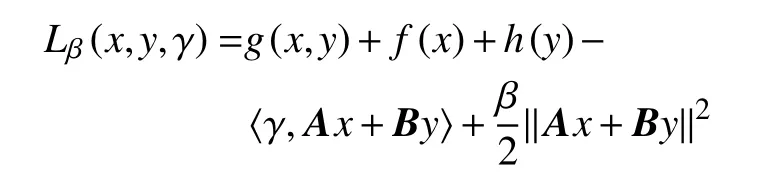




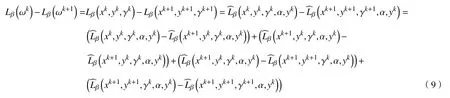


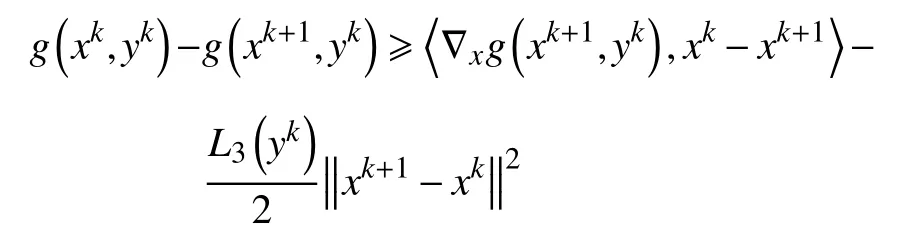
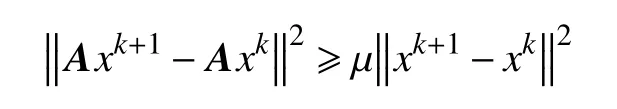




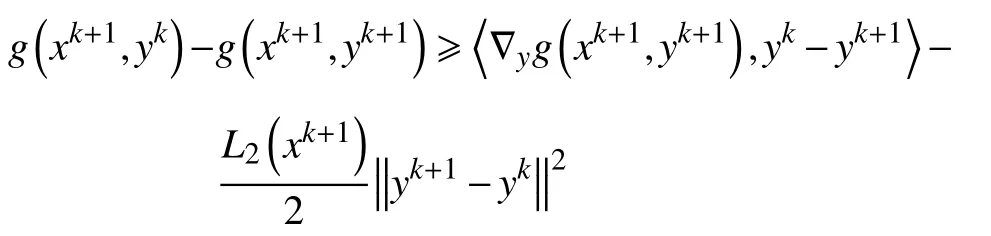

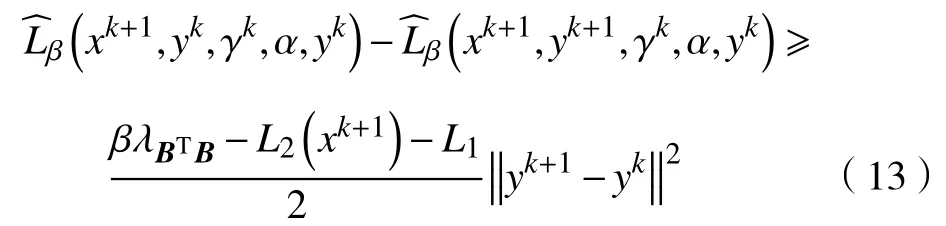
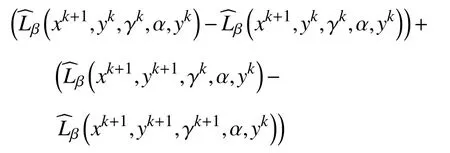

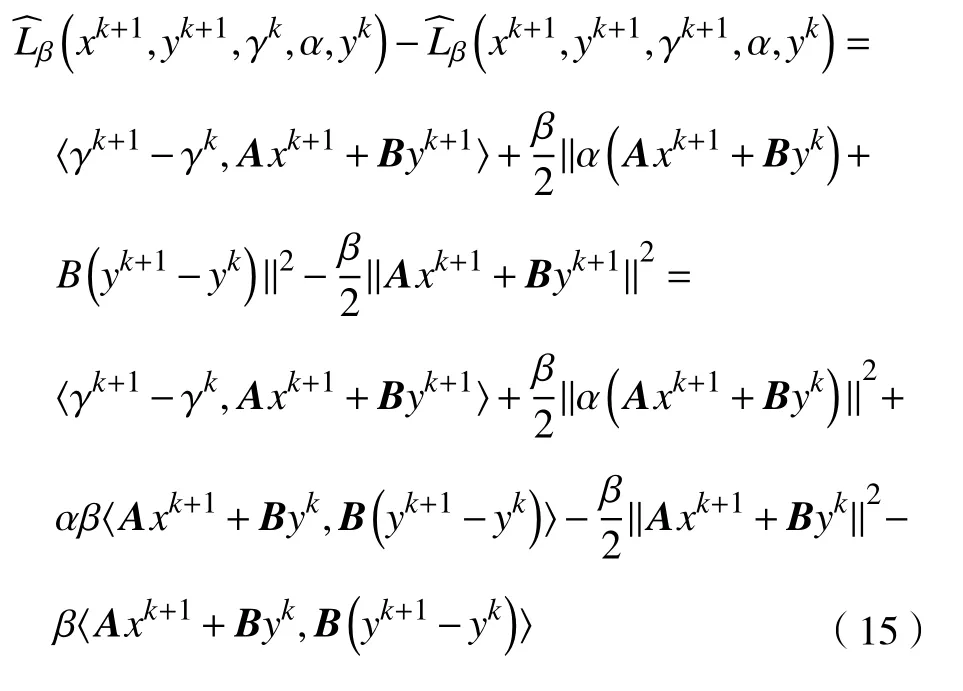

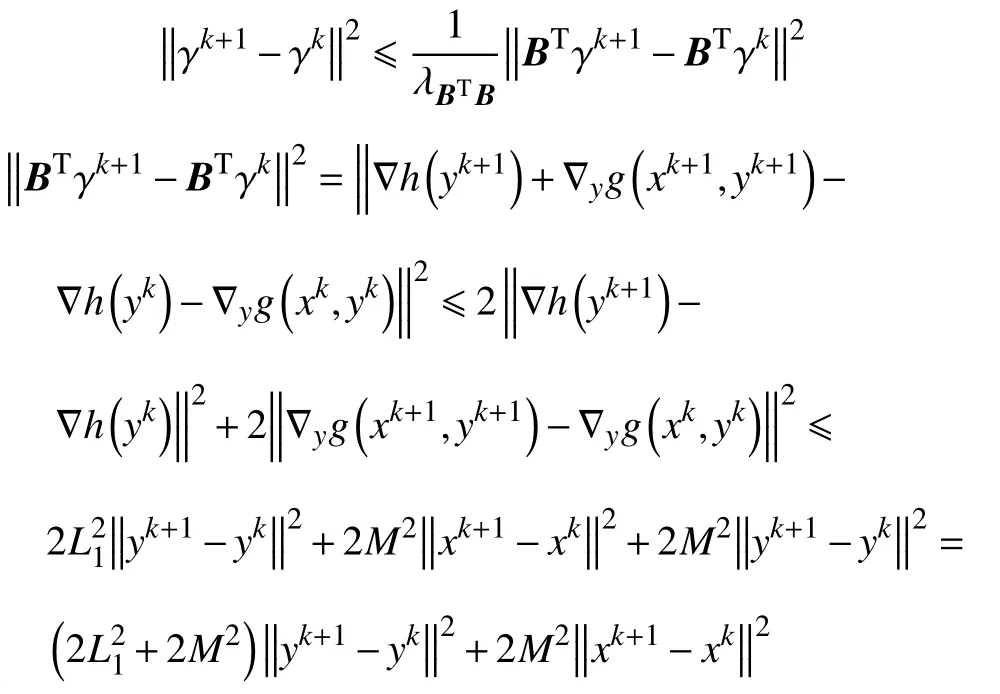
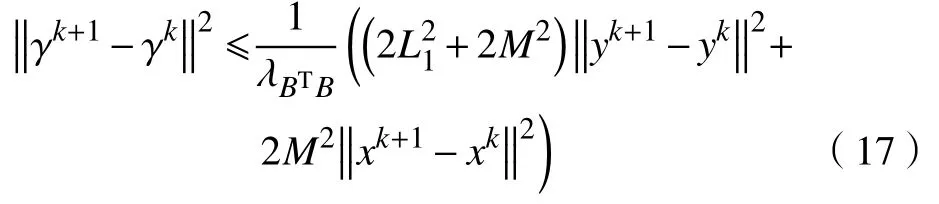



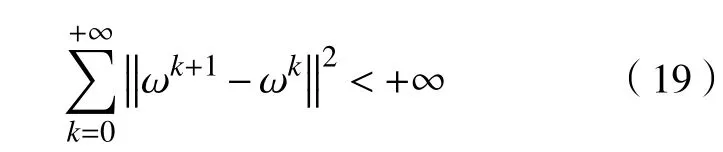




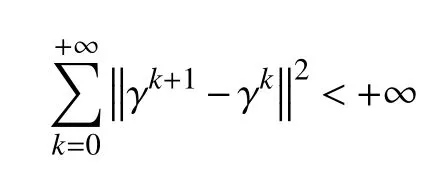
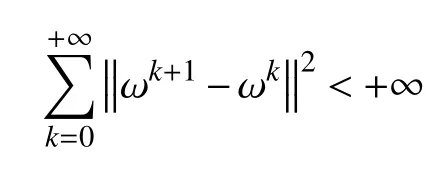



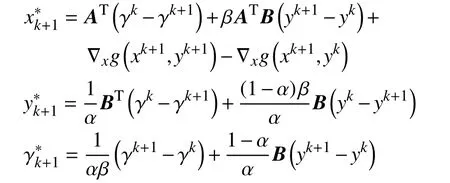
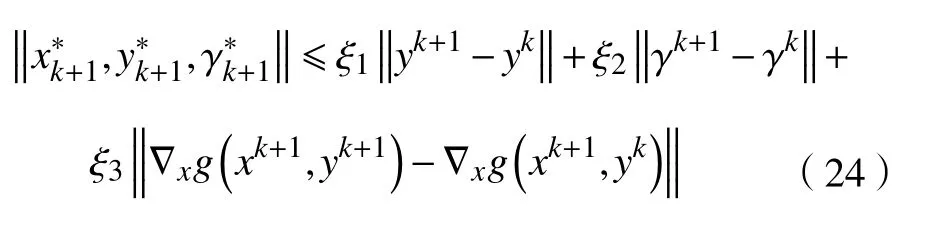
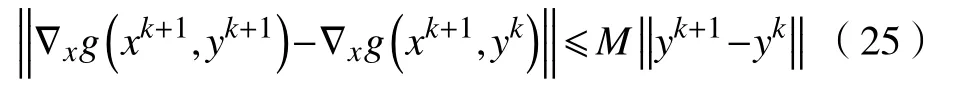
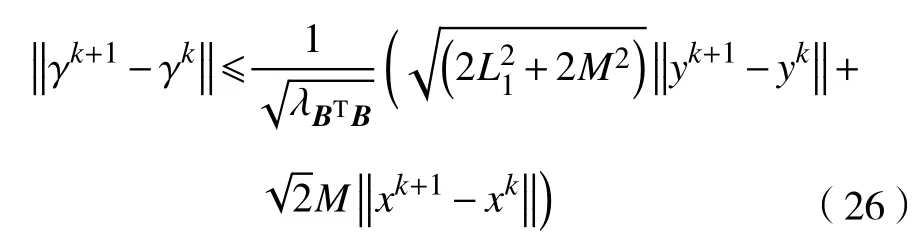
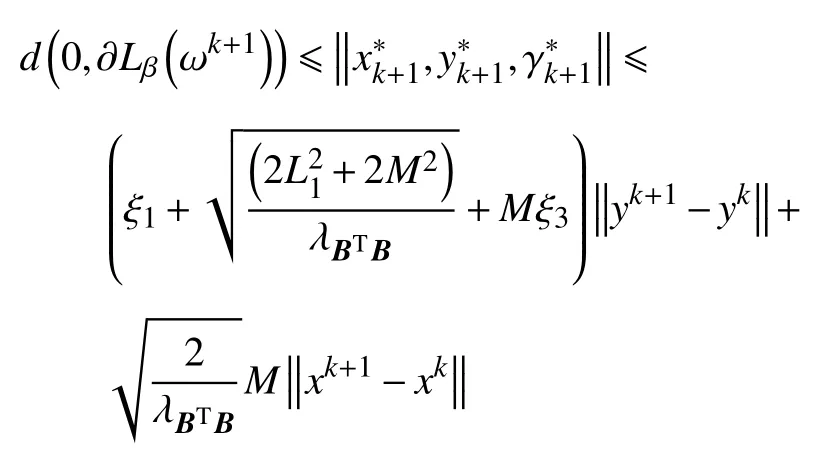

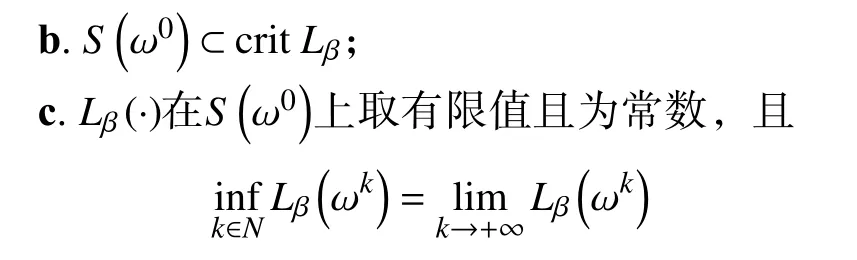
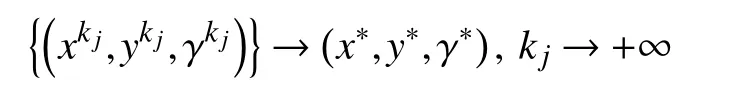
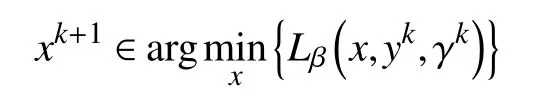

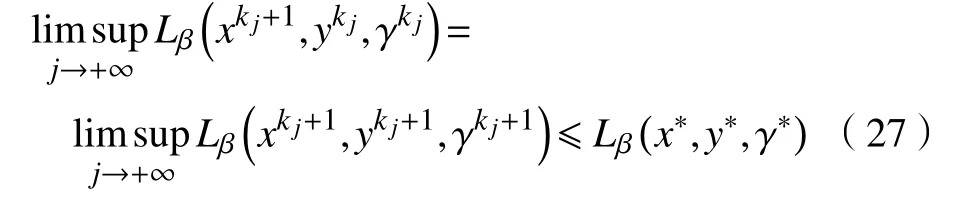

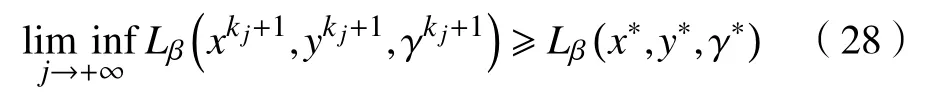



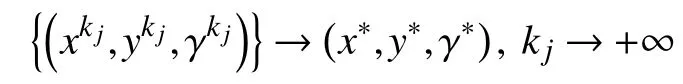
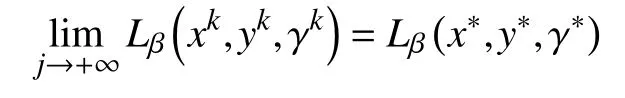


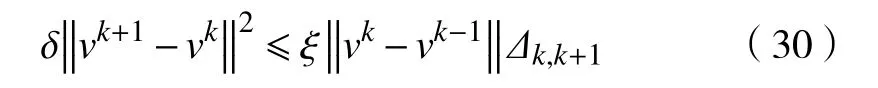

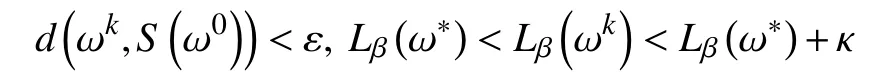










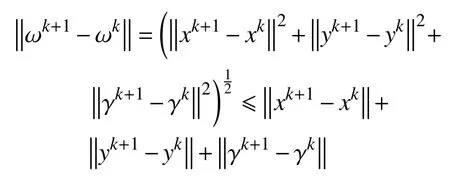

4 结 论

