基于扩展观测器的电液负载模拟器自适应鲁棒控制
邹 璇, 刘鑫宇, 赵海鸣, 沈 伟
(1.中国船舶集团公司第七〇三研究所,哈尔滨 150000;2.上海理工大学 机械工程学院,上海 200093)
电液负载模拟器具有响应快、跟踪精度高和输出能力大[1]的优点,被广泛应用于航空航天、汽车工业等领域[2-4]。然而,作为典型的非线性时变系统[5],电液负载模拟器具有复杂的建模不确定性,包括参数时变性、无法建模的非线性因素,同时还会受到来自舵机系统的运动干扰,这极大地增加了开发高精度和高性能控制器的难度。为了解决上述问题,众多先进的非线性控制策略相继被提出,例如,采用滑模变结构控制策略克服无法建模的模型不确定性[6-7]、采用自适应控制策略在线估计时变参数和外部扰动[8]、利用观测器对外部扰动进行观测和补偿[9-10]等。这些控制策略可以在一定程度上提高电液负载模拟器的跟踪性能,然而,在实际应用中,由于采用基于无噪声理论的全状态反馈设计,对位移、速度及加速度等状态信号的测量行为会不可避免地将测量噪声引入控制器。这些测量噪声会干扰控制器的自适应性能和观测器的在线估计效果,从而劣化系统的跟踪性能表现,这成为了进一步提高控制精度的障碍。
为了降低测量噪声,Sadegh等[11]提出了一种基于期望轨迹补偿的控制策略,通过构造不含测量噪声的状态变量的期望值来代替被污染的实际状态,从而有效地降低测量噪声对系统的影响。文献[12-13]将该补偿技术引入到自适应控制器的设计中,提出了基于期望轨迹补偿的自适应鲁棒控制策略并应用于电机系统,Yao等[14]也将这种技术运用到电液执行器的运动控制当中,并取得了较好的效果。然而,在对外部干扰的处理上,该策略只是简单地将其作为时变参数进行自适应估计,自适应效果只依赖于状态误差,这对于系统跟踪精度的提升是有限的。
基于以上问题,本文提出了一种基于扩展观测器的自适应鲁棒控制器,将未知的外部干扰扩展为系统的高阶状态,并对其进行估计和补偿,同时,将实际的状态变量值替换为对应的期望信号值,并将其集成到自适应模型补偿器和扩展观测器中以降低测量噪声的影响,同时提升控制器的自适应性能和观测器的观测性能,观测器的系统参数由控制器的参数自适应率获得。此外,控制器中还引入了一个虚拟的误差变量,以使控制器获得额外的设计自由度,从而获得更高的控制性能。最后,利用Lyapunov理论证明了该控制策略的稳定性。仿真结果验证了该控制器不仅具有出色的跟踪性能,还具有较强的鲁棒性。
1 电液负载模拟器系统模型
系统模型如图1所示,左侧为电液负载模拟器,右侧为舵机系统。系统工作时,舵机系统会对负载模拟器施加额外的运动干扰。惯性负载的动力学方程为
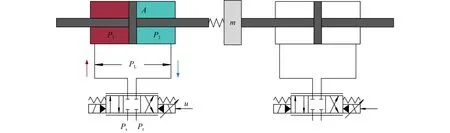
图1 电液负载模拟器结构示意图Fig.1 Schematic diagram of the structure of electro-hydraulic load simulator

式中:m与y分别为负载的质量和位移;PL为负载压力,PL=P1−P2;A为液压缸的有效作用面积;Cf(y˙)为连续的摩擦模型函数;Am为摩擦振幅;B为黏性阻尼系数;d(t,y,y˙)表示总的模型不确定性,包括由舵机系统产生的外部扰动和无法测量的建模误差。
液压缸的压力动态方程为

式中:V为液压缸两腔的总容积; βe表示液压油的有效体积模量;Ct是液压缸的内部泄漏系数;Q(t)为未建模的流量误差;kt是控制输入电压u的总流量增益;Ps是 供油压力;Pr为回油压力;sgn(u)为不连续的符号函数。

系统末端的输出力

式中,k为力传感器的弹簧劲度系数。
定义状态变量为x=[x1,x2,x3]T=[y,y˙,APL/m]T,则整个系统可以由以下状态空间方程表述:

其中,

2 自适应鲁棒控制器设计
2.1 参数自适应算法设计
由于实际应用中,液压系统参数会因为工作环境变化而出现波动,为了减少系统的参数不确定性以及提高跟踪性能,在控制器设计中引入了参数自适应算法。定义一组未知参数集:θ=[θ1,θ2,θ3,θ4,θ5,θ6]T,其中,θ1=b,θ2=Am/m,θ3=4Aβekt/(mV), θ4=4A2βe/(mV), θ5=4βeCt/V, θ6=qn(t)。由此,描述系统的状态空间方程 (5 )可写为

在进行控制器设计之前,需要作假设。
假设1期望运动轨迹及其导数均有界。Fd(t)为期望跟踪的力。此外,系统中外部扰动及其导数、建模误差均有界,即:

其中, δ1, δ2, δ3均为正数。
假设2系统参数的波动范围为:

式中:Ωθ为有界开集;θmin=[θ1min,···,θ6min]T,θmax=[θ1max,···,θ6max]T,且全部已知。
定义映射函数

自适应律设计为
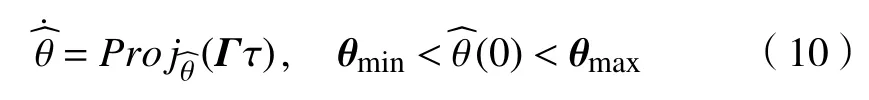
式中, Γ为正定的自适应对角矩阵。
对于任何函数 τ,该自适应率都将满足以下关系[15]:
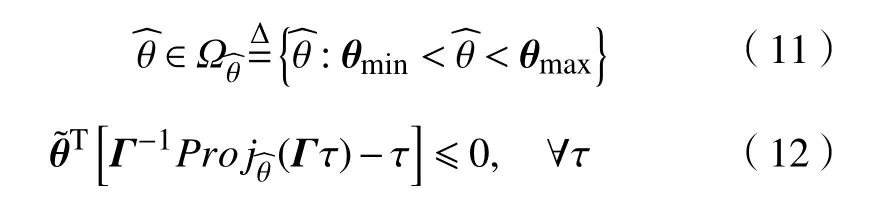
2.2 扩展观测器设计
来自舵机系统的运动干扰d(t)是影响电液负载模拟器跟踪性能的主要干扰源,通过构造扩展观测器[10],将系统内的模型不确定性作为系统的高阶状态来估计。
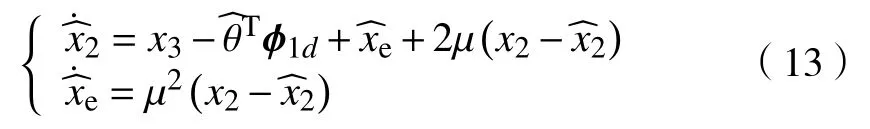
结合系统模型 (6 ),观测器误差的动态误差可以表述为

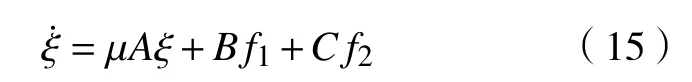
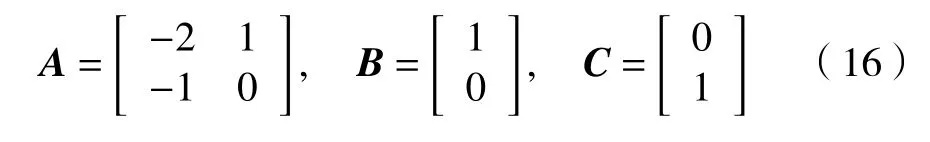
由于A是一个Hurwitz矩阵,因此,必定存在一个对称正定矩阵P,满足以下Lyapunov方程:

其中,E为单位矩阵。求解上述等式,可得
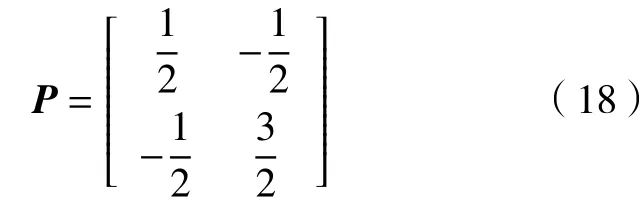
2.3 控制器设计
现介绍控制器设计步骤。
步骤1定义一组误差变量,

式中:z1为输出的位移误差,z1=x1−yd;c1,c2为正反馈增益系数;s为辅助误差变量,用于获得额外的控制器设计自由度。
在设计时,可以将x3视为虚拟输入量,从而为其合成虚拟控制率 α。将式 (1 9)和式 (2 0)代入式(21),并对其求导,可得
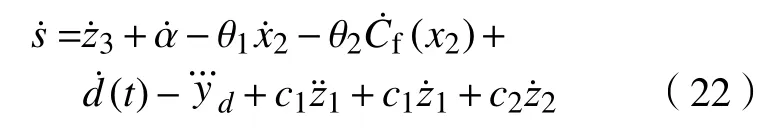
基于式(22),虚拟控制率 α可以设计为

式中: αa为基于模型的在线参数自适应前馈补偿控制律; αs为待合成的鲁棒控制律; ︿xe为观测得到的外部扰动量。
由于模型存在不确定性,并且自适应参数的估计值与其真实值之间存在误差,因此,需要设计鲁棒控制律来稳定系统。
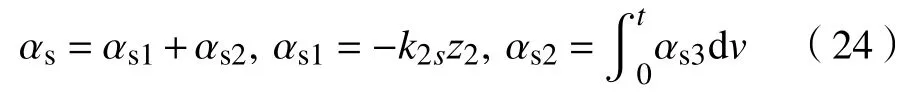
式中: αs1用于稳定系统的标称模型;k2s是一个正常数反馈增益; αs2用于镇定未知的模型不确定性以及平衡系统的参数不确定性。
αs3可以是满足:
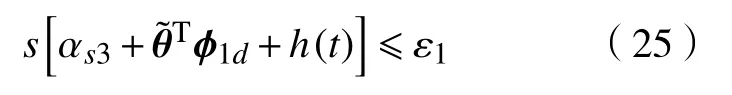

条件的任意函数。
ε1为一个任意小的常数。因此, αs3可以被设计为如下形式:

式中,k2a为正的常数反馈增益。
将式(14),(23),(31)代入式(22),可得

步骤2合成系统的实际控制律u。将式 (6 )的第3式和式 (2 0)代入式 (2 8),可得

在上述的控制器设计中,x2被y˙d代替参与了控制器的补偿设计。为了降低测量噪声的干扰,构造实际控制律u还 需要知道x3的期望值信息,从式(6)的第2式可知,x3可被表达为
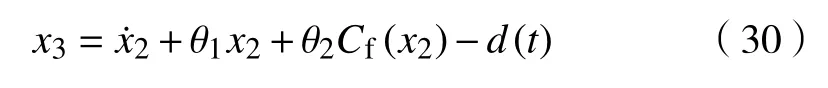
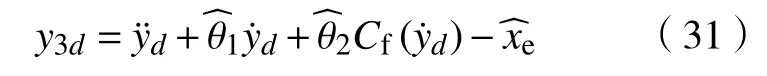
考虑到式 (2 3),x3可表达为

式(29)可写为
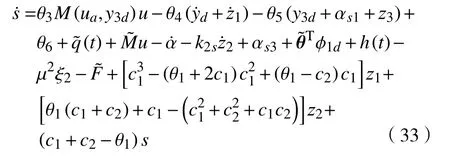
其中,

而ua是将要合成的实际控制律u中的基于模型的自适应补偿控制律。
类似于先前的虚拟控制律 α的设计,最终的实际控制律u设计为
式中:ua为基于模型的自适应补偿控制律;us1用于稳定系统标称模型;us2用于控制系统的模型不确定性和平衡系统的参数不确定性。

式中,k3s是一个正常数增益反馈。
us2可以是满足

条件的任意函数。

其中, ε2为一个任意小的常数。因此,us2可以被设计为
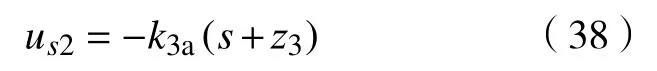
其中,k3a为正的常数反馈增益。
将式(34)和式(35)代入式(33),可得
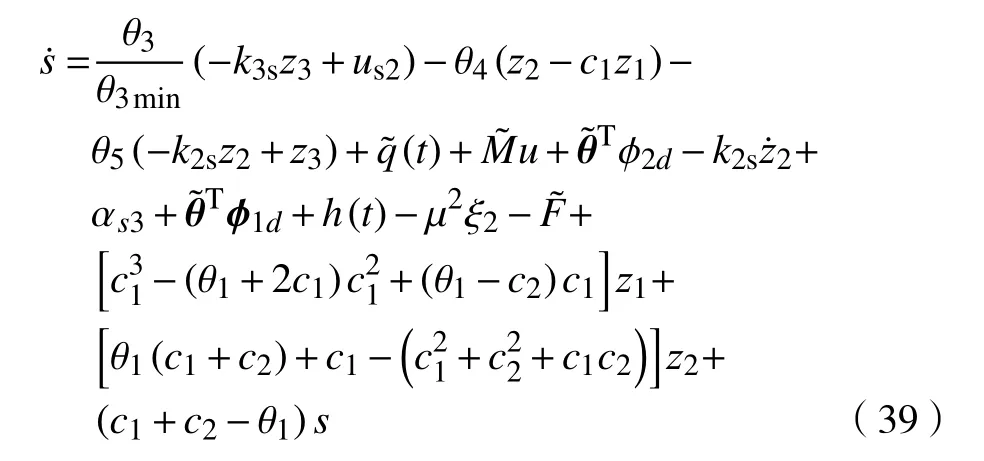
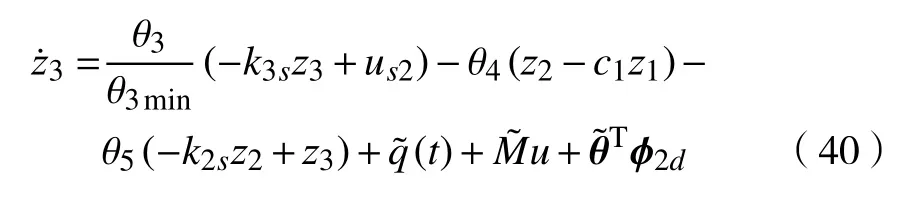
2.4 稳定性分析
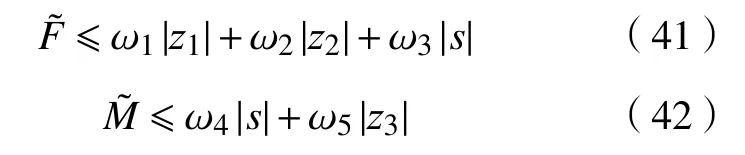
式中, ω1, ω2, ω3, ω4, ω5均为正常数。
系统参数的估计值通过自适应律式(10)进行更新,其中, τ被设计为

当反馈增益c1,c2,k2s,k3s和 µ足够大时,以下的矩阵将正定:

其中,


由上可知,提出的控制律就能够保证控制器的收敛性和系统的稳定性。
证明当h(t)=0且q˜ (t)=0时,定义Lyapunov函数VA。

结合式 (15),(19),(21),(39),(40),并对式(46)求导 后 同时引入式 (12),(26),(37), (41)~(43),整理可得

由Young’s不等式,可得:

将式(44),(45)和(49)代入式(48),可得
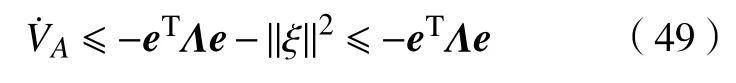
其中,e=[z1,z2,z3,s,ξ1,ξ2]T。则所有信号均闭环有界,控制器是渐近稳定的,即t→∞时,z1→0。
当h(t)≠0且q˜ (t)≠0时,定义函数VB。

对VB求导后考虑式(25)和式(36),可得

其中, θM= θmax−θmin,由Young’s不等式可得

根据式(45),式(53)可转换为

从而得到
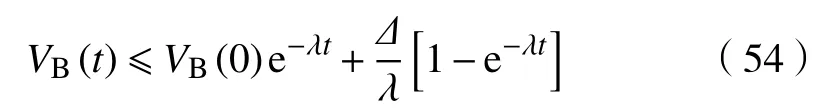
其中, λ =2λmin(Λ), λmin(Λ)表示正定矩阵 Λ的最小特征值。由上可知,所提出的控制器不仅可以确保所有信号均为闭环有界,且呈指数级收敛,其收敛速度和最终跟踪误差取决于 λ。
3 仿真分析
在MATLAB/Simulink中搭建系统仿真模型并对提出的控制策略进行仿真分析[16],仿真步长设置为0.001 s,电液负载模拟器的仿真参数如表1所示。

表1 系统仿真参数Tab.1 Parameters of system simulation
此外,非线性摩擦函数选择为
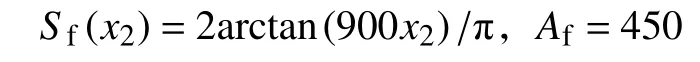
为了验证所提出的控制器的控制效果,选择3种性能指标,即最大跟踪误差Me、平均跟踪误差µe, 跟踪误差的标准偏差 σe来量化各种控制策略的控制性能[17]。同时,选择本文提出的控制器与PI控制器和DCAC控制器进行对比。
a.ARC-ESO。这是本文提出的具有扩展观测器的自适应鲁棒控制器,控制参数为:c1=400,c2=200,k2s=400,k3s=200,k2a=1,k3a=0.5,µ=1000。105,0,−1000]T,θmax=[250,25,540,4.1×107,1000,1000]T。参数自适应率矩阵Γ =diag{20,1×10−6,5×10−3,50,0.75,10}。
b.PI。PI控制器。通过试错法调整的控制器增益为KP=5800,KI=2000。
c.DCAC。具有期望轨迹补偿的自适应控制器[14],其结构为

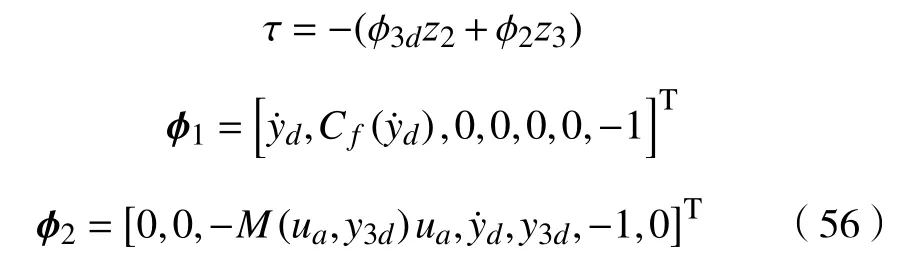
其中,y3d为x3的期望值。参数估计初始值和其界限以及自适应率矩阵为

其余控制参数与ARC-ESO相同。
仿真实验分为以下两种工况:a.舵机系统未加载时各控制策略的控制效果对比;b.舵机系统加载时各控制策略的控制效果对比。仿真测试中,参考力轨迹设定为Fd(t)=4000arctan(sin πt)[1−exp(−t)]N。同时,系统位置、速度、压力信号均添加了幅值为 1× 10−5的随机噪声信号[18],以模拟测量噪声。
工况1舵机系统未加载时,外部扰动设定为d(t,y,y˙)=0,3种控制器各自的跟踪误差如图2所示,除根据系统实际跟踪轨迹和期望目标轨迹之间的实时偏差值评估控制算法性能外,本文还采用了其他3个性能指标量化估计每种控制算法的性能,即误差最大值Me, 误差平均值 µe,误差标准偏差 σe。
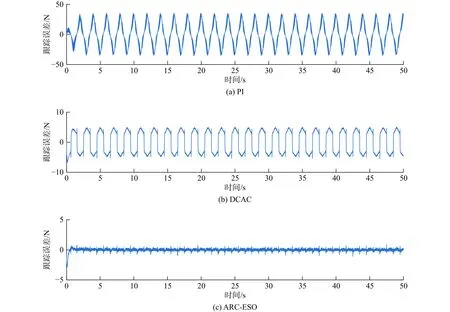
图2 3种控制器的跟踪误差(工况1)Fig.2 Tracking error of three controllers (condition 1)
a.误差最大值定义为
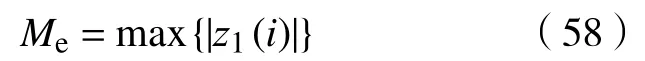
其中,i=1,2,···,n,n为所记录的误差数据的数量。
b.误差平均值定义为

c.误差标准偏差定义为
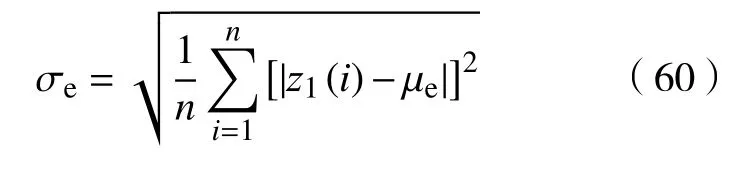
跟踪性能指标如表2所示。
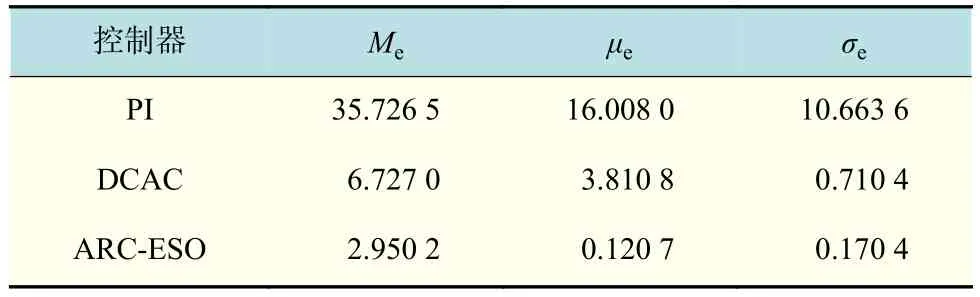
表2 跟踪性能指标(工况1)Tab.2 Tracking performance metrics (condition 1)
仿真结果表明,在此工况下,PI控制器作用下系统的跟踪效果最差,其最大误差达到了35 N。相比之下,由于具有基于期望模型补偿的前馈控制律,在DCAC控制器作用下,系统最大稳态误差为5 N左右。由于引入的辅助误差变量和自适应干扰观测器,本文所提出的ARC-ESO控制器具有最佳的跟踪性能,其最大跟踪误差不超过3 N,而最大稳态误差不超过1 N,与其他2种控制器相比,各项性能指标都有较大幅度的提升。
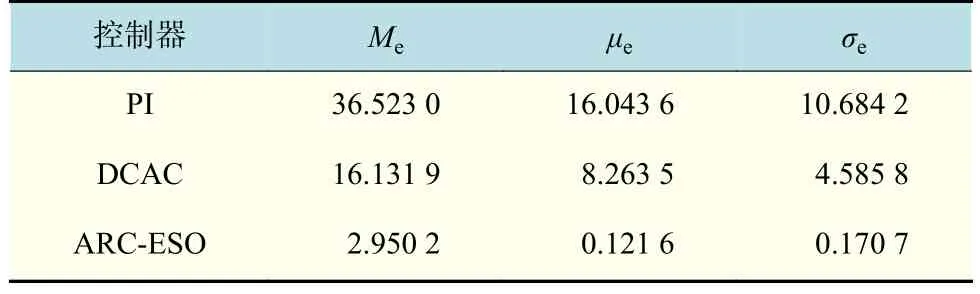
表3 跟踪性能指标(工况2)Tab.3 Tracking performance metrics (condition 2)
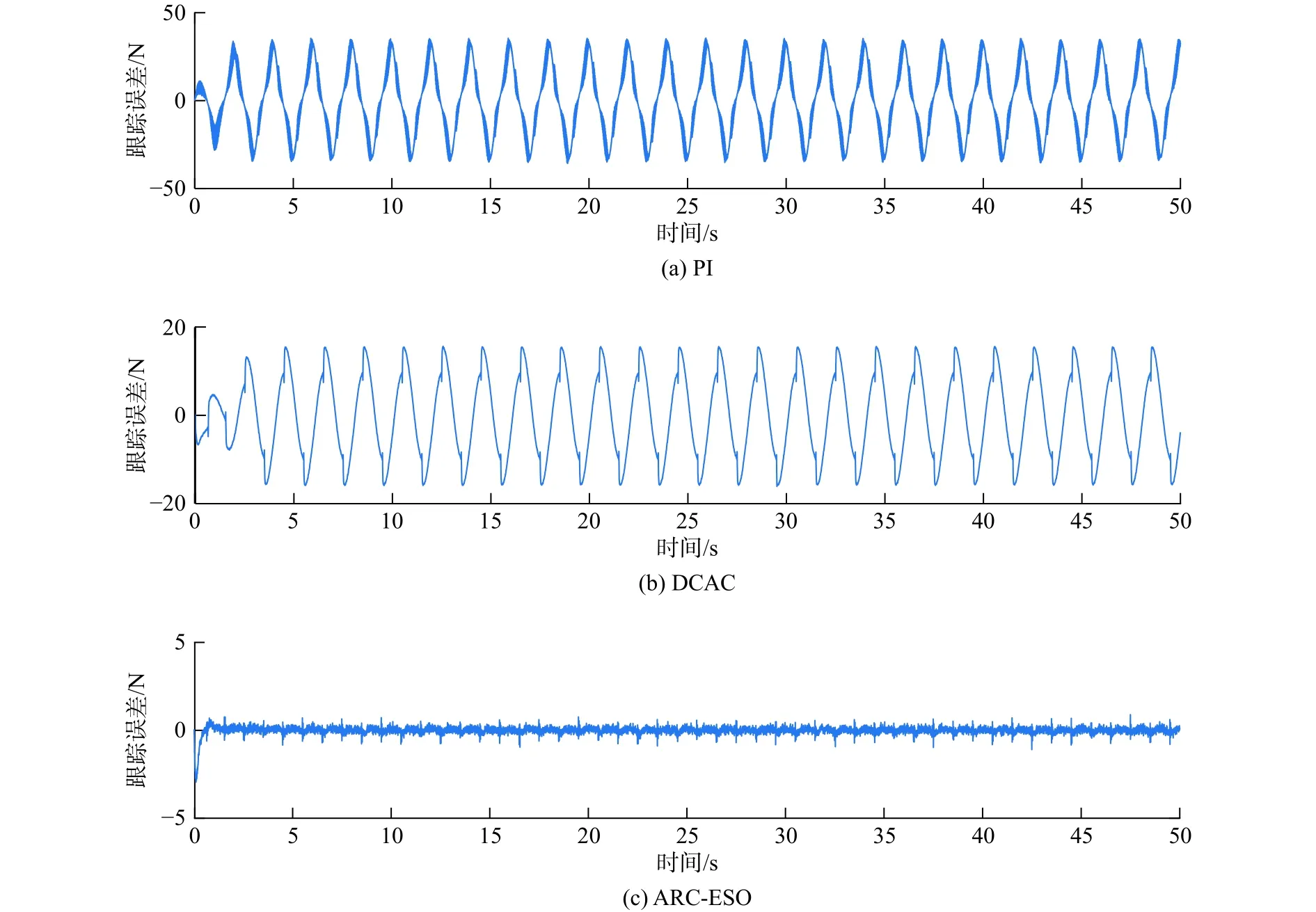
图3 3种控制器的跟踪误差(工况2)Fig.3 Tracking error of three controllers (condition 2)
仿真结果表明,当系统中加入外负载扰动后,与工况1相比,PI控制器受外负载扰动的影响较小,但PI控制器的跟踪精度仍然是最低的。而DCAC控制器的控制性能劣化得较为严重,系统最大稳态误差达到了16 N,各项性能指标都具有大幅度的衰减,尽管DCAC将外负载干扰作为了系统参数进行自适应估计,但自适应效果十分有限。而ARC-ESO依然获得了最佳的控制性能,与工况1相比,在其作用下的系统跟踪精度衰减非常微小,表明本文所提出的控制策略具有良好的抗干扰能力。
4 结 论
针对电液负载模拟器中传感器测量噪声和未知的外界干扰引起的跟踪精度不高的问题,提出了一种高精度的自适应鲁棒控制策略。在考虑存在非线性特性和各种建模不确定性的情况下建立了电液负载模拟器的数学模型;通过构造扩展观测器在线估计外部干扰并进行补偿,利用系统各状态变量的期望信号代替实际状态信号,并集成到参数自适应模型补偿器中,以减少测量噪声对控制器和观测器的影响。同时通过引入一个虚拟的误差变量来改进控制器结构,以提高跟踪精度。该控制器已通过Lyapunov方法证明了其闭环稳定性,并利用MATLAB/Simulink进行了仿真分析。结果表明,与PI和DCAC控制器相比,在不存在外部扰动的情况下,所提出的控制器能够达到更高的跟踪精度,而在存在外部扰动的情况下,所提出的控制器不仅保持了良好的跟踪性能,同时具有较强的鲁棒性。

