柔性基础下不排水桩复合地基固结分析

白银川， 杨 涛

（上海理工大学 环境与建筑学院，上海 200093）

以桩体为竖向增强体的复合地基技术不仅使地基承载力得到了极大提高，还会增强路基边坡的稳定性，减少地基沉降和工后沉降并加快其固结过程，在世界各国软土地基加固工程中得到越来越广泛的应用。

复合地基固结理论一直是复合地基理论研究的核心问题之一。砂桩和碎石桩等散体材料桩的刚度较小但渗透性远大于桩间土，散体材料桩加速复合地基固结的机理较为明确。国内外学者基于砂井地基固结理论，考虑桩体应力集中效应提出了大量散体材料桩复合地基的固结计算模型。CFG桩、低强度混凝土桩和水泥土桩都为不排水桩，刚度较大但不排水，不排水桩复合地基的固结机理比较复杂。Horpibulsuk等[1]进行了水泥土桩复合地基固结特性室内模型试验，发现端承桩复合地基比天然地基的固结要快很多，Chai等[2]认为这主要是加固区复合固结系数远大于地基土固结系数的缘故。杨涛等[3]和章定文等[4]分别采用数值模拟和室内模型试验的方法，对悬浮和打穿软土的不排水桩复合地基的固结特性作了比较分析，发现后者比前者固结更快，桩的贯入比较小时不排水悬浮桩复合地基的固结甚至比天然地基还要慢。卢萌盟等[5]和Gong等[6]分别在变荷载作用下得到端承不排水桩和悬浮水泥土桩复合地基的固结解析解。朱洵等[7]和陈宙翔等[8]分别建立了瞬时荷载下考虑桩间土非饱和和非线性的端承不排水桩复合地基固结解析解。杨涛等[9-10]给出了变荷载下悬浮钉形搅拌桩复合地基和瞬时荷载下多元不排水长–短桩复合地基的固结计算模型。张丹贝等[11]考虑真空作用，建立了悬浮不排水桩复合地基的固结解析解。

上述不排水桩复合地基固结计算模型都是在桩土等竖向应变假设下建立的。然而，在路堤等柔性基础下以及带柔性垫层的刚性基础下的复合地基中，桩与桩间土的沉降不同，桩的沉降比桩间土小，路堤下复合地基中这种现象更为明显。显然，这些情况下等竖向应变假设并不成立。李耀琨等[12]和Lang等[13]分别建立了刚性基础下有垫层端承和悬浮刚性桩复合地基的固结解析解，可以考虑桩体上、下刺入的影响。目前，柔性基础下不排水桩复合地基固结计算理论的研究成果较少。杨涛等[14-15]对此进行了初步研究，在等应力条件下给出路堤下端承不排水桩复合地基的固结解析解，但解答中复合压缩模量仍然采用基于等应变假设的面积比公式计算，且解答不能揭示路堤荷载下桩土差异沉降的影响机理。显然，进一步研究柔性基础下不排水桩复合地基固结计算方法是非常必要的。鉴于此，本文建立了考虑桩–土间差异沉降的端承不排水桩复合地基固结简化解析解，可为同类实际工程设计提供参考。

1 基本假定与轴对称固结模型

1.1 基本假设

公式推导采用如下基本假设：

a.桩为不排水桩。桩和桩间土都为线弹性体，它们仅发生竖向变形，桩–土界面处不发生相对滑移。

b.桩间土是饱和的，仅发生竖向渗流，渗流符合达西定律。

c.外荷载p(t)大面积施加，在待加固地基中引起的竖向附加应力σ(t)沿深度均布。

1.2 轴对称固结模型

柔性基础下复合地基的轴对称固结模型如图1所示。不排水桩的半径和长度分别为rp和H，其弹性模量和压缩模量分别为Epe和Ep。单桩影响区半径为re，它与桩间距s及布桩方式有关：三角形布桩时re=0.525 s，正方形布桩时re=0.565 s。不排水桩的置换率m=(rp/re)2。桩间土的竖向渗透系数、泊松比、弹性模量及压缩模量分别为kv，μs，Ese和Es。由于是柔性基础，大面积均布荷载p(t)施加在复合地基表面上，任意时刻桩顶沉降为wp(t)，同一时刻桩间土表面任一点的沉降为ws(r,t)，后者大于前者。r和z为径、竖向坐标。

图1 复合地基固结模型Fig.1 Consolidation model of the composite ground

2 固结方程及其解答

2.1 固结方程

根据Alamgir等[16]的研究，p(t)作用下柔性基础下复合地基中桩顶沉降wp(t)和桩间土表面沉降ws(r,t)存在下述关系：

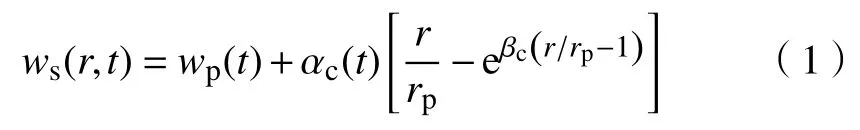
式中，αc(t)和βc为待定的位移参数，前者随加荷过程而变化。

根据任意时刻固结模型外边界r=re上的剪应力为0，可以得到βc满足如下超越方程：

式（2）表明βc只与桩的置换率m有关。求解方程式（2）可以得到βc随桩置换率m的变化规律，如图2所示。拟合后可得到二者的如下关系：

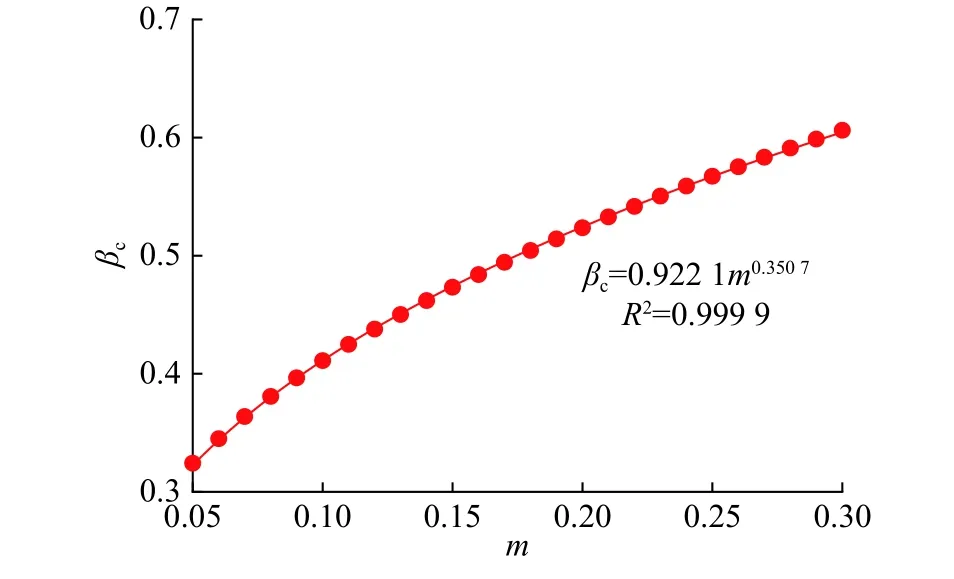
图2 βc随不排水桩置换率变化曲线Fig.2 Variation of βc with area replacement ratio of undrained column

将轴对称固结模型离散化，如图3所示。将桩分成L个单元，各单元厚度ΔH=H/L；将桩间土分成L×N个环状单元，其厚度等于桩单元的厚度，径向宽度 ∆r=(re–rp)/N。参照Alamgir等[16]和杨涛[17]的推导过程，可以得到αc(t)的计算公式如下：

图3 固结模型的离散Fig.3 Discretization of consolidation model

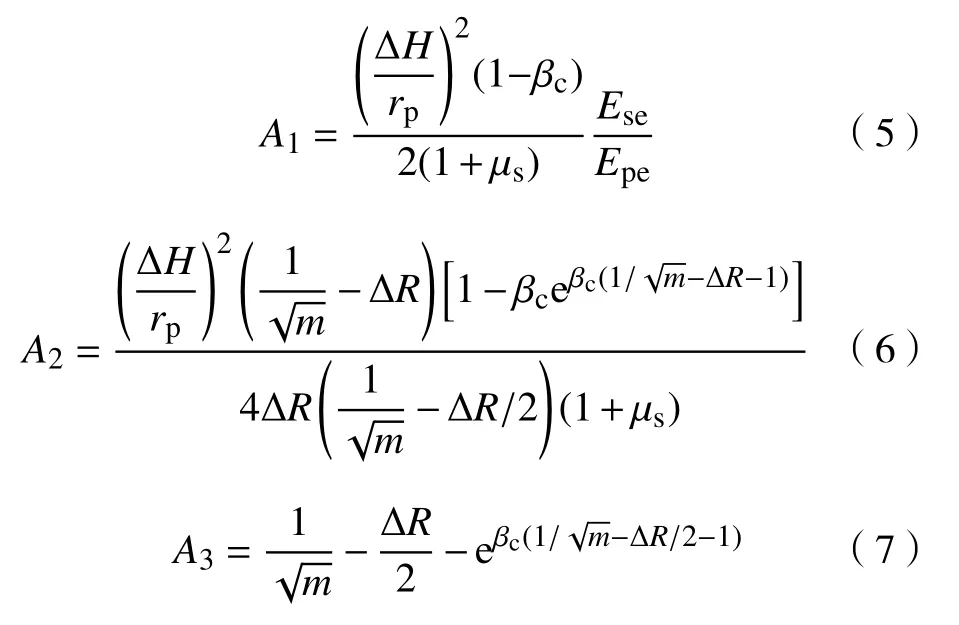
式中，ΔR=Δr/rp。

由于 σ¯p(t)沿桩长并不均布，从式（4）可知αc(t)沿桩长也不均布。根据Alamgir等[16]的研究可知，它沿桩长的分布需要从上到下逐个对桩单元和模型外边界处土单元进行应力计算才能获得，工作量较大。参照杨涛[17]的研究，复合地基固结分析中可采用不随桩长变化的 α¯c(t) ，计算公式如下：

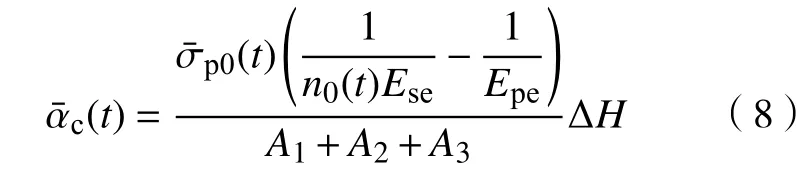
柔性基础下桩–土差异沉降随距桩中心线距离的增加而逐渐增大。利用式（1）可计算出t时刻桩顶平面桩–土平均差异沉降δ(t)：

式（9）表明，δ(t)随加荷过程逐渐变化。

参照李耀琨等的研究[12]，桩间土与桩的竖向应变之间存在下述关系：

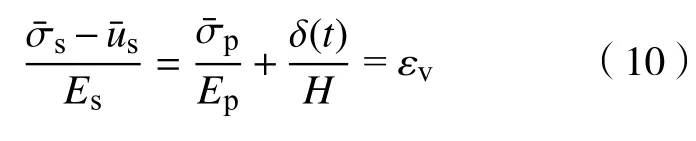
将式（9）代入式（10），并取 αc(t)=(t)，有

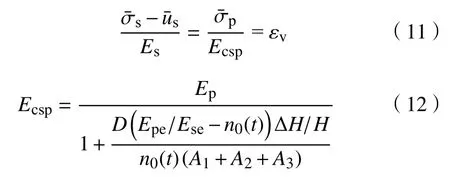
式中，D为常数，按下式计算：

吴慧明等[18]和方磊等[19]分别进行了柔性基础下不排水桩复合地基现场试验和室内模型试验，李国维等[20]进行了填砂路堤下水泥土搅拌桩复合地基现场试验。这些试验发现：柔性基础下不排水桩复合地基桩土应力随荷载变化的规律与刚性基础下的复合地基显著不同，它随荷载的增加先减小后增大然后趋于稳定，最大值约为1.8，地基土的固结时间对其数值影响较小。此外，杨涛等[3]的研究表明，桩土应力比的变化对柔性基础下不排水桩复合地基固结速率的影响不大。基于这些研究成果，建议固结分析时桩土应力比n0(t)取2～3。

根据复合材料力学理论，待加固天然地基中竖向附加应力σ(t)为复合地基的平均竖向应力，则任意深度处σ(t)由桩和土共同承担，有

由式（11）和式（14）可得

由桩间土质量守恒定律，有

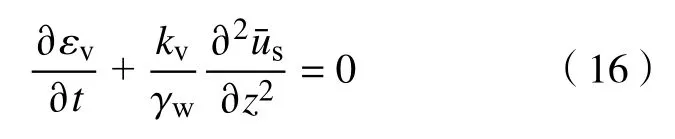
式中，γw为水的重度。

将式（15）代入式（16）可得变荷载下柔性基础下复合地基桩间土的固结控制方程：

式中，cv=kvEs/γw为桩间土的竖向固结系数。

2.2 定解条件

考虑复合地基顶面排水底面不排水，变荷载下固结方程（18）的定解条件为

a.竖向边界条件。

b.初始条件。

2.3 变荷载下固结一般解

在定解条件式(19)～(21)下不易求解非齐次的固结方程式(17)。为便于数学上求解，进行如下函数变换：

将式(22)代入固结方程式(17)和定解条件式 (19)～(21)，有

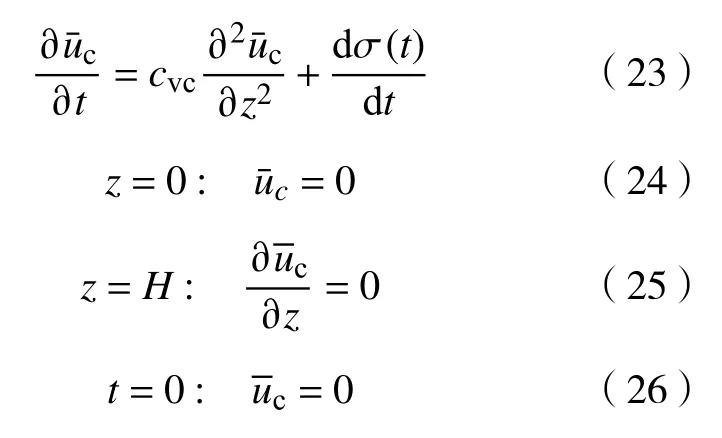
由于上述变荷载下复合地基平均超静孔压定解问题的数学表述与相同荷载下天然地基一维固结问题定解问题的数学表述在形式上完全相同，根据Lu等[21]天然地基一维固结理论，容易解得复合地基平均超静孔压为

式中，M=(2i–1)π/2，i=1, 2，3,···,∞。

将式（27）代入式（22），得到桩间土的平均超静孔压:

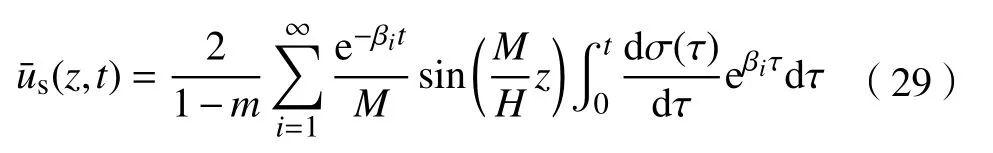
利用式（27）给出的复合地基平均孔压解答，按式（30）计算变荷载柔性基础下复合地基的整体平均固结度：

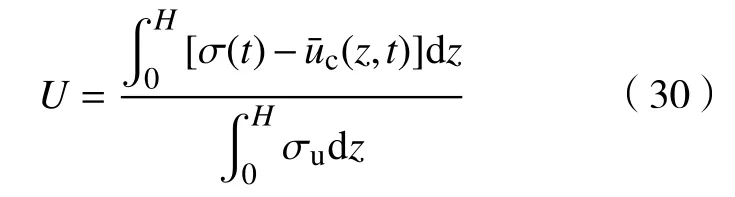
式中，σu为待加固地基中竖向附加应力的最终值。

2.4 单级荷载下的解答

特殊地，考虑单级加荷情况。图4给出单级外荷载作用下待加固天然地基竖向附加应力σ(t)随时间变化的曲线，它可表示为

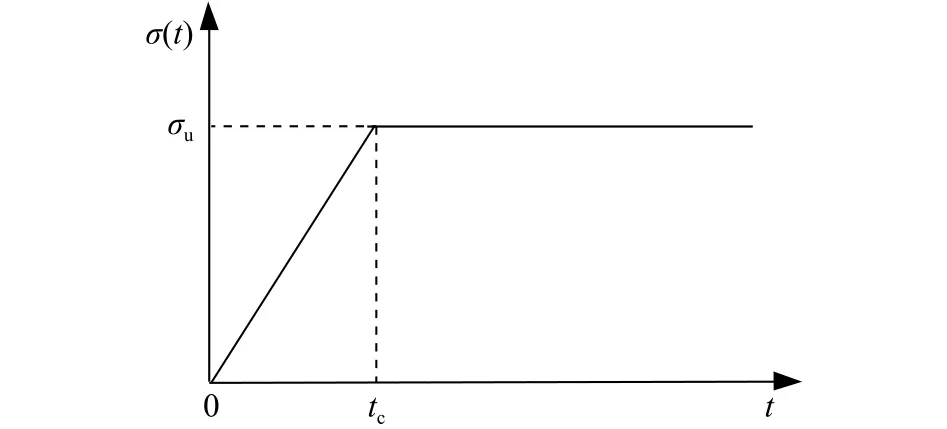
图4 单级荷载下竖向附加应力曲线Fig.4 Vertical additional stress curve under ramp loading

式中，tc为加载时间。

将式（31）代入式（27），得到单级荷载下复合地基的平均超静孔压：

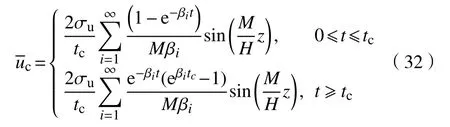
将式（32）代入式（22）即可得到单级荷载下桩间土的平均超静孔压：

将式（31）和式（32）代入式（30），得到单级荷载下复合地基的整体平均固结度：

3 算例验证

工程设计中将路堤视为柔性基础，故算例选取路堤下端承水泥土桩复合地基进行固结分析。软土地基厚度为H=20 m，无黏性土路堤高度为4 m，重度为 17 kN/m3。水泥土桩半径rp=0.25 m，单桩影响区半径re=0.7 m，相应的置换率m=12.8%。水泥土桩、路堤填土和桩间土的压缩模量、泊松比和渗透系数列于表1中。路堤单级填筑，每层0.5 m，总填筑时间tc=90 d。

表1 各材料参数Tab.1 Parameters of different materials

对路堤下水泥土桩复合地基进行比奥固结有限元分析，采用ABAQUS有限元软件进行计算。由于固结模型具有对称性，取其右半部分进行计算，如图5所示。模型左、右边界分别为对称轴和外边界，数值计算时约束左、右边界的径向位移，底部径、竖向位移均约束。复合地基的表面排水，二侧边界和底边界均不排水。各材料均采用线弹性模型，其弹性模量Et可根据它们的压缩模量E1和泊松比μ按式Et=(1+μ)(1–2μ)E1/(1–μ)近似估算。路堤土和桩用轴对称4结点四边形单元（CAX4）离散，桩间土用轴对称4结点四边形应力–孔压耦合单元（CAX4P）离散，共剖分6720个单元，结点数为6989个。图6给出复合地基有限元网格示意图。

图5 有限元模型Fig.5 Finite element model

图6 有限元网格Fig.6 Finite element mesh

图7给出本文解析解和有限元解获得的路堤荷载下端承水泥土桩复合地基整体平均固结度U随无量纲时间因数Tv=cvt/H2的变化曲线，解析解计算时n0=2.0，L=20，N=6。图中也给出了卢萌盟等[5]基于等应变假设的固结解析解的计算结果。从图7中可以看出，本文固结度解析解计算的复合地基固结度曲线与有限元数值解的结果非常接近，两者之差的绝对值不超过1.7%，说明本文解析解具有较高的计算精度。由于采用了等应变假设，卢萌盟等[5]解析解计算的复合地基固结度数值大于本文解析解和有限元解，它与有限元解之差的绝对值不超过5.9%。假设桩土等应变后固结度的数值偏大，原因在于高估了柔性基础下复合地基的刚度，即高估了不排水桩刚度的影响。本算例Ecsp=107 MPa，数值要小于桩的压缩模量Ep=150 MPa。此外，图7还表明，等应变假设下端承不排水桩复合地基的固结速率与路堤下复合地基固结速率的数值差别并不大。

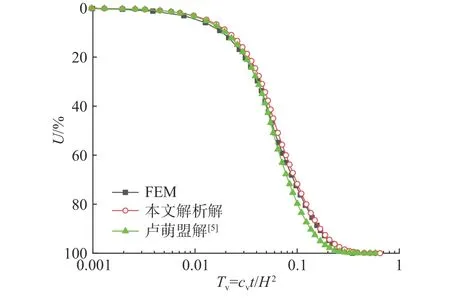
图7 不同解析解与有限元解的比较Fig.7 Comparison of various analytical solutions with FEM result

图8给出由本文解析解、李耀琨等[12]解析解和卢萌盟等[5]等应变解析解获得的复合地基固结度曲线的比较。李耀琨等[12]的解答考虑了设置垫层的刚性基础下复合地基桩–土沉降的不同，利用半无限弹性地基上圆形基础沉降计算公式计算复合地基桩–土差异沉降，没有考虑相邻桩的影响。图8表明，采用李耀琨等[12]解析解计算的水泥土桩复合地基的固结速率要大于本文解析解的计算结果，二者最大差值约4.3%，较之有限元解，二者最大相差约5.1%，其固结度曲线更靠近卢萌盟等[5]的等应变解答。

图8 本文解析解与其他解析解的比较Fig.8 Comparison of the proposed solution with several existing solutions

为考察桩土应力比对复合地基固结速率的影响，用本文解析解计算出不同桩土应力比下水泥土桩复合地基的固结度曲线，如图9所示，桩土应力比n0取2，3，5和7。图9表明，不同桩土应力比下复合地基的固结度曲线较为接近，说明对于诸如路堤等柔性基础下的水泥土桩复合地基，其固结速率对桩土应力比的变化不敏感，这与杨涛等[3]的数值模拟结果是一致的。n0从2变化到7时复合地基固结度略微增大，最大增幅不超过2.5%。图9表明本文固结解析解中桩土应力比n0取值2～3是合理的。

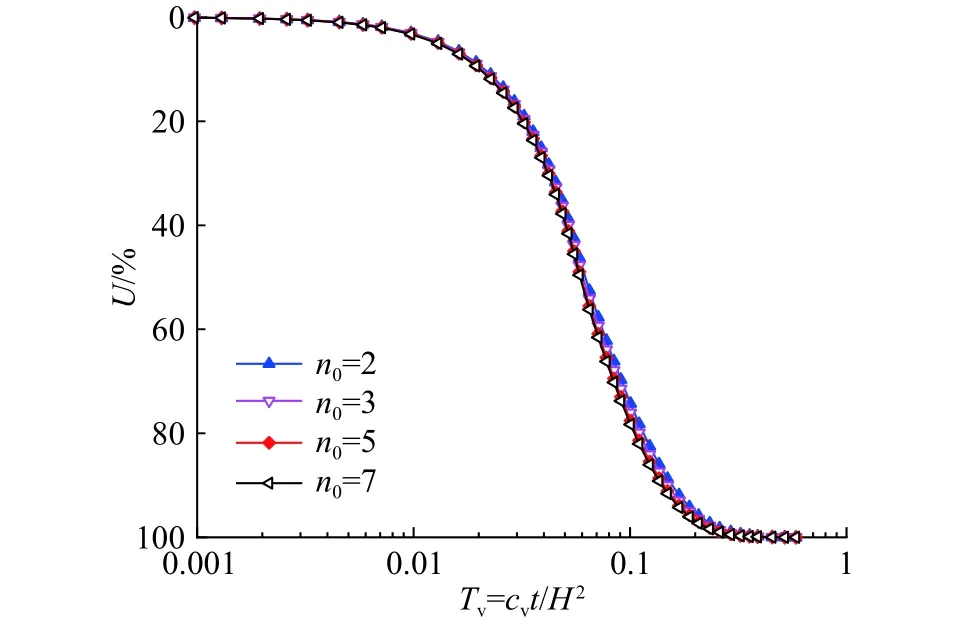
图9 桩土应力比对固结速率的影响Fig.9 Influence of column-soil stress ratio on the consolidation rate

4 结 论

a.建立了柔性基础下端承不排水桩复合地基固结解析解，可用于路堤荷载下不排水桩复合地基的固结分析。

b.本文固结度解析解与有限元解具有较好的一致性，计算精度高于现有的考虑桩–土差异沉降的固结计算模型。

c.桩土应力比对固结速率的影响不大。对柔性基础下的水泥土桩复合地基可取2～3。

d.基于等应变假设的不排水桩复合地基固结计算模型更适合刚性基础下复合地基的固结分析。如果将它们用于路堤荷载下端承不排水桩复合地基固结分析，计算出的固结速率数值偏大。