如何充分体验“怎样围面积最大”

□王 利

在“圆的面积”教学之后，教师可以通过以下教学过程，让学生充分体验“用一根绳子围出一块地，怎样围面积最大”。

一、通过列举加强对比

1.呈现题目：有两根长度相等的绳子，用它们分别围成长方形，怎样围面积会更大？

2.学生猜测、列举数据进行验证，全班交流。

3.得出结论：用绳子围长方形，在周长一定的情况下，围成正方形时面积最大。

二、通过计算加强对比

1.呈现题目：一根绳子长31.4米，如果用这根绳子在操场上围出一块地，怎样围面积最大？

2.学生交流：可以围成正方形。同时提出疑问：围成圆形面积会不会更大？

3.学生独立计算，展示方法。

方法一：围成正方形。

31.4÷4=7.85（米），7.85×7.85=61.6225（平方米）。

方法二：围成圆形。

31.4÷3.14÷2=5（米），5×5×3.14=78.5（平方米）。

因为78.5＞61.6225，所以用一根长31.4米的绳子围图形，围成圆形时面积更大。

4.举多个例子后得出结论：用周长一定的绳子围图形，围成的图形中，圆的面积＞正方形的面积。

三、通过画图加强对比

1.变化题目：一根绳子长31.4米，在操场上围出一块地，如果一侧靠墙。怎样围面积最大？

2.小组交流，得出不同的围法（如图1）。

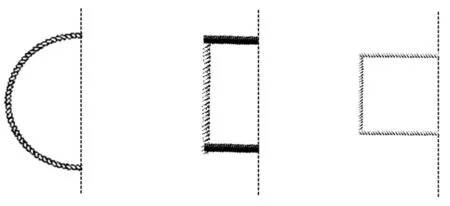
图1

3.提问：运用得出的规律，可以判断这三种围法谁的面积最大吗？

引导学生把这面墙看作对称轴，分别画出每个图形的另一半来进行判断。当学生分别画出半圆、长方形（长度是宽度的2倍）、正方形的另一半时，结果一目了然。因为周长一定时圆的面积最大，所以当每个图形面积都减少一半，周长还是一定，这时半圆的面积就是最大的。

得出结论：周长一定时，一面靠墙来围，围成半圆形面积最大。

四、通过公式加强对比

1.呈现题目：用一根绳子，直接围成一个圆与靠墙围成一个半圆相比（如图2），谁的面积更大呢？

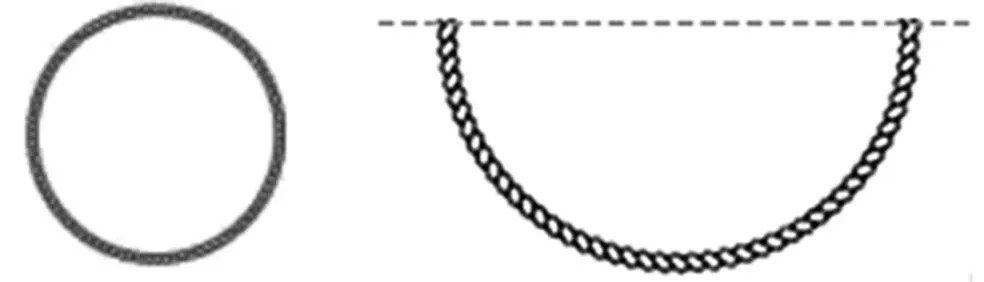
图2

由d1=r2，可得d1:d2=1∶2，那么S圆∶1S圆2=1∶4，所以也就是当周长一定时，一侧靠墙围成的半圆形的面积是独立围成的小圆面积的2倍。

以上教学过程，能够让学生学会从多个角度分析、解决问题，便于他们在遇到问题时灵活地选择解决问题的方法。