基于数据分布信息的相关滤波器算法研究

蒋琦，周刚

（四川大学锦江学院计算机学院，眉山 620860）

0 引言

图像识别与检测是计算机视觉的重点研究领域，相关滤波器算法因其简单的实现方法和较优秀的实现效果成为该领域的研究热点［1］。相关滤波器是利用图像中目标之间的相关性进行判别，其中相关性指的是图像信号的相似性，相关滤波器利用一定数量的训练数据的相关性得到滤波模板，然后通过滤波模板判断其他图像中目标与模板的相似程度［2］。因此，相关滤波器最重要的研究内容就是如何得到滤波模板。众多研究人员提出了大量算法，并取得了不错的实验效果。文献［3］提出了无约束最优权衡综合判别函数滤波器（unconstrained optimal trade-off synthetic discrimi⁃nant function，UOTSDF），通过平衡参数优化一个判别函数来得到滤波器。文献［4］提出了最优权衡综合判别函数滤波器（optimal trade-off synthetic discriminant function，OTSDF），这种滤波器在思想上与UOTSDF是一致的，不同之处在于有无约束条件。文献［5］提出了平均合成精确滤波器（av⁃erage synthetic exact filter，ASEF），先求出单张图像的弱滤波器，再集合多个弱滤波器求均值得到一个强滤波器；文献［6］提出了最小输出误差平方和滤波器（minimum output sum of squared error，MOSSE），通过高斯函数产生峰值，最小化实际相关输出与期望输出误差的平方和而得到滤波器。文献［7］改变思路，将支持向量机［8］（support vector machine，SVM）的思想引入相关滤波器，在最大化响应峰值的同时最大化分类间隔，提出了最大间隔相关滤波器（maximum margin correlation filter，MMCF）。MMCF利用了SVM优秀的分类泛化性能，兼顾大间隔原理和最小化样本均方误差，使这种相关滤波器相比传统的相关滤波器在性能上获得了较大提升。

但是，MMCF在结合SVM的同时，并未考虑到SVM存在的问题。SVM在建立分类超平面时只利用了边界上的样本点，忽略了样本的整体结构信息以及样本之间的结构联系，因此所得的超平面并不一定符合样本实际结构信息，而MMCF也继承了这个缺点。为了解决上述问题，本文提出两种方法进行改进，两种算法都是充分利用样本数据的结构信息，提高所得训练模板的识别和检测效果。

1 相关工作

本节首先简要介绍SVM，再对相关滤波器和MMCF进行简要阐述。

1.1 支持向量机

SVM是一种经典的分类算法，在当今计算机视觉领域仍然发挥着重要的作用［9］。SVM提取训练样本的特征，在样本特征空间寻找样本点的最大间隔，通过建立分类超平面尽量分隔不同类别的样本，以达到分类的目的。在实际训练中，SVM的求解其实是使该超平面与任一样本之间的最小L-2范数距离最大化。设有一数据集为U=则SVM的定义如下：

其中，w是分类超平面法向量，b为偏置量，ξ为松弛变量，T表示转置，C为惩罚系数，y i为样本标签，x i是输入数据x i的向量形式。SVM在众多的分类应用中取得了不错的效果，但仍然存在一些问题，并没有考虑样本的结构信息和内在联系。

1.2 最大间隔相关滤波器

相关滤波器利用模板与目标的相关性进行判别，其主要研究问题为求解出滤波模板w。传统的相关滤波器可以被看作为优化输入图像的理想期望相关输出与训练图像和模板的相关输出之间的欧式距离［10］。相关滤波器定义为：

其中，⊗为互相关运算，g i为期望相关输出，不同的相关滤波器算法所构建的g i并不相同。

大多数相关滤波器的改进思路都集中于g i的构建上，但改进效果都有一定局限性。文献［7］将SVM的思想引入相关滤波器，提出了MMCF，进一步提升了相关滤波器的鉴别能力。MMCF的定义为：

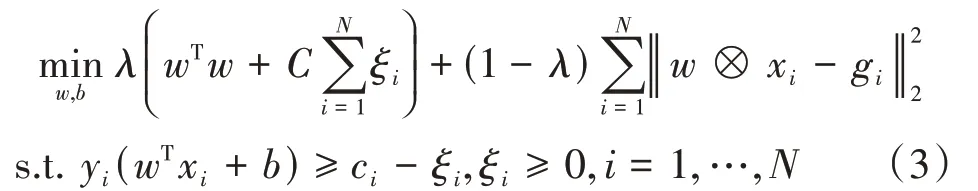
其中，w既是分类超平面法向量，也是滤波模板，λ为平衡系数，用于平衡支持向量部分和相关滤波部分的权重，c是一个与样本有关的常量。MMCF利用SVM和相关滤波各自的优点，提升了相关滤波器的实验效果。但同时也继承了SVM的缺点，样本的训练并不充分。

2 算法原理

为了解决MMCF所存在的未利用样本整体分布信息和样本内部联系的问题，本文提出了两种方法，分别是基于最小类内方差和最小类局部保持方差的相关滤波器。

2.1 基于最小类内方差的相关滤波器

SVM在建立分类超平面时未考虑样本整体信息，致使MMCF在训练时同样存在这个问题。针对SVM这一问题，文献［11］提出了将Fisher线性判别的思想与SVM结合起来，提出了最小类内方差支持向量机（minimum class variance support vec⁃tor machine，MCVSVM）。设有一数据集为U={x i||i=1,…N}⊂Rd×N，且分别属于两类{A+,A-}，则MCVSVM的定义如下：

其中，S w为类内散度矩阵，其定义为：

其中，m A是A类样本的均值。类内散度矩阵用于描述异类样本的整体分布情况。因此，在加入S w之后，SVM所计算的最大距离由欧式距离变更为马氏距离。

受MCVSVM的启发，为了解决MMCF存在的问题，也可将类内散度矩阵引入MMCF，提出了最小类内方差相关滤波器（minimum class variance correlation filter，MCVCF），其定义如下：

其中，MCVCF将类内散度矩阵加入到模型中，在训练时充分利用每一类样本的整体分布信息，能得到更加鲁棒的滤波器。

但模型（6）并不能够直接进行应用，还需要进行求解。且根据相关卷积定理［12］，相关滤波器的相关运算需通过傅里叶变换转换到频域中变换为相乘运算，能极大提高运算速度。因此，需先将模型（6）转换到频域中，再利用wolf对偶问题进行求解。

将模型转换到频域，由于MCVCF由两部分构成，所以转换过程可以分为两个部分。首先对模型中的支持向量部分进行傅里叶变换，内积在变换过程中只是按1d的比例进行了缩放，d是样本数据的维度则该部分变换之后如下：

其 中，̂是 频 域 中 的w，b'=b×d，̂=是频域中A类的均值，̂是频域中的x，†表示共轭转置。

相关滤波部分的转换如下：

其中，是对角线元素为所有元素的对角矩阵，分别是x i、g i经过傅里叶变换转换到频域的数据。另外忽略掉1d，因为它是一个常数，对最终效果没有影响。̂可改写为：

其中，1=[ 1…1]T，将式（9）代入式（8）：

完成对两个部分的傅里叶变换，合并成MCVCF的频域形式：

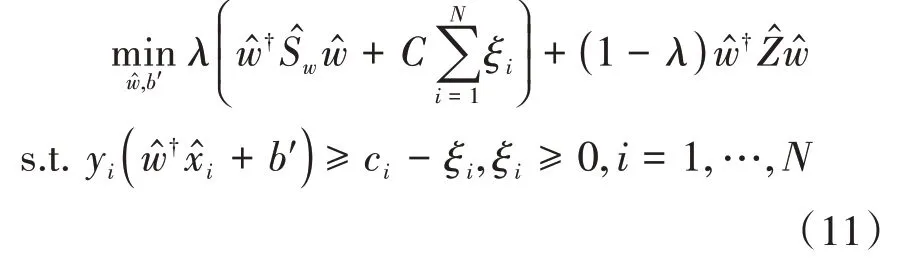
可通过Lagrange对偶问题对式（11）进行求解，首先构造式（11）的Lagrange函数：

其中，αi、βi是Lagrange乘子，再对式（12）求偏导：

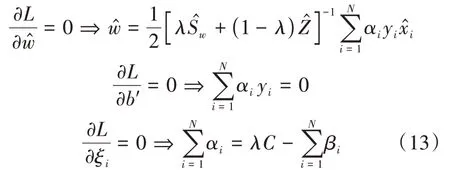
将式（13）的结果代入式（12），可得MCVCF的对偶问题：

其中，α=[α1,…,αN]T。得到式（14）后，使用SMO算法进行求解，通过该算法求得Lagrange乘子向量α*，则可利用下式求解MCVCF在频域中的滤波器向量̂：

其中，Y是对角线元素为y i的对角矩阵。̂是频域中的滤波器向量，在实际应用中，还需要将其通过傅里叶逆变换转换到空间域，并根据样本数据大小转换为相同尺寸的滤波模板矩阵W*，便可利用W*与待测试图像进行互相关运算以求出相关性。

2.2 基于最小类局部保持方差的相关滤波器

在结合SVM的同时，MMCF同样未考虑到样本内部的结构信息。针对SVM这一事实，文献［13］利用局部保持投影［14］的思想，提出了最小类局部保持方差支持向量机（minimum class locality preserving variance support vector machine，MCLPVSVM）。设有一数据集为U={x i|i=1,…,N}⊂Rd×N，则MCLPVSVM的 定 义如下：

其中，Z w是局部保持散度矩阵，用于描述数据内部的结构信息。设有K=1,2两类样本数据，则Z w的定义如下：

其中，Z K是第K类数据的局部保持散度矩阵，其具体构造如下：

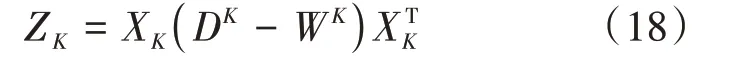
其中，X K是第K类数据的矩阵形式，D K是一个对角矩阵，其元素的定义是是W K矩阵的元素，W K是邻接图权重矩阵，设x Ki、x K j是第K类样本的数据点，G是数据集U的邻接图，G用于表示数据局部流型结构，L=D-W是G的拉普拉斯矩阵。G共有N个节点（即数据点），如果节点i在节点j的k个最近邻居中，则x Ki∈N K(x Kj)，以高斯核的形式构造权重矩阵W K，其元素的构造形式如下：

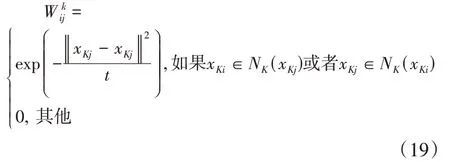
其中，t是高斯核函数参数。

MCLPVSVM较好地解决了SVM未考虑样本内部结构的问题，因此，可将局部保持散度矩阵引入MMCF，提出最小类局部保持方差相关滤波器（minimum class locality preserving variance correla⁃tion filter，MCLPVCF），其定义如下：

其中，Z w是局部保留散度矩阵，其定义与式（17）、（18）、（19）相同。

MCLPVCF的求解与MCVCF的求解过程基本一致，最终求解出的MCLPVCF的频域滤波器向量是：

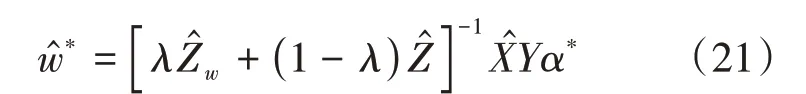
在实际应用中，仍需要将转换到空间域中，得到空间域滤波器W*。

3 实验及结果分析

为了验证所提算法的有效性和参数对模型的影响，本节将进行仿真实验，并在相同实验条件下与MOSSE、OTSDF、MMCF、最大间隔矢量相关 滤 波 器［15］（maximum margin vector correlation fil⁃ter，MMVCF）、零混叠大间隔相关滤波器［16］（zero-aliasing maximum margin correlation filter，ZAMMCF）进行对比。所有实验都是基于Intel i5处理器、16 GB内存、MATLAB R2020a的应用环境。

3.1 参数影响

为了讨论参数对所提算法的影响，首先将进行手写数字识别的实验。本实验采用的是MINIST标准手写体数字数据集，这个数据集包含70000张手写体数字。为了便于参数讨论，从中随机挑选1000张图像进行实验，其中800张作训练集，200张作测试集。

MCVCF的参数主要有λ和C，表1给出了在不同的参数设置下MCVCF的识别率。从表1数据可以看出，λ和C的设置对识别率有一定的影响，总体来看，在λ=0.5和C=0.1左右识别率相对较高，在λ=0.7和C=1时识别率最高。

表1 不同参数下MCVCF的识别率（%）

MCLPVCF有k、λ、t和C四个参数，参数讨论相较复杂，C对实验结果的影响与MCVCF类似，因此本文只讨论k、λ、t对MCLPVCF的影响。图1给出了参数k、λ、t不同组合下的手写数字识别的识别率。其中（a）是固定参数C=1、λ=0.6时的识别率，（b）是固定参数t=1、C=1时的识别率，（c）是固定参数k=30、C=1时的识别率。可以看出，三个参数对MCLPVCF的实验结果有一定的影响，三个参数的共同点在于在数值偏小时识别率都较低，在增大到一定程度时识别率会趋于平稳。

图1 参数k、λ、t对MCLPVCF识别率的影响

3.2 检测实验

为了进一步验证所提算法的有效性，本部分将进行人眼检测实验，并与其他相关滤波器算法作对比。此实验采用的是Yale人脸数据集，此数据集包含15类的165张人脸图像。从中选择一部分人工标注剪切人眼作训练集，再从另一部分随机选择15张图像作测试集。本实验MCVCF固定参数λ=0.6、C=1，MCLPVCF固定参数λ=0.6、C=1、k=5、t=1.5，MMCF、MMVCF和ZAMMCF固定参数λ=0.6、C=1，OTSDF固定参数λ=0.6。本实验的评价指标是检测准确率，所有算法所检测出的人眼标注框与真实人眼标注框重合率大于0.3时认为检测到了人眼，以检测到的目标数与总体图像数的比值作为检测准确率。

如图2是MCVCF和MCLPVCF的实验效果图，其中黑色虚线框为MCVCF标注的人眼位置，红色实线框为MCLPVCF标注的人眼位置。

图2 MCVCF、MCLPVCF人眼检测效果

表2给出了所提算法与其他相关滤波器算法的实验结果。能够看出，MCVCF和MCLPVCF的检测准确率相较所比较的大部分相关滤波器算法有所提升。

表2 不同滤波器的检测准确率（%）

3.3 识别实验

相关滤波器的另一个重要应用领域就是目标识别，因此本部分将进行一个物体识别和一个人脸识别实验。具体实验方法为：采用一对多的策略，选择其中一类图像为正类，其他类为负类，经过多次实验求得平均识别率和标准差。

物体识别实验采用的是COIL100物体数据集，这个数据集包含100类的7000张彩色图像，所有图像中的物体都进行了校准处理，并呈现出不同的角度。为了实验的方便，将数据集中所有的图像缩小为60×60大小，随机选择每类的［20，25，30，35，40，45］张图像作训练集，其他图像作测试集，重复测试40次求得平均识别率。本实验中，MCVCF固定参数λ=0.6、C=1，MCLPVCF固定参数λ=0.6、C=1、t=0.5，在训练集图像数目为20、30、35时k=3，其 余 情 况k=2，MMCF、MMVCF和ZAMMCF固定参数λ=0.6、C=1，OTSDF固定参数λ=0.6。

COIL100的实验结果如表3所示，所提两种算法的平均识别率相比其他算法都要更高，尤其相比MMCF，MCVCF能提高0.9%～1.4%，而MCLPVCF则能提高1.5%～5.6%。

表3 不同滤波器在COIL100数据集上的平均识别率及标准差（%）

人脸识别实验采用的是AR人脸数据集，这个数据集包含120个人的3120张图像。随机选择每类的［5，10，15，17，20］张图像作训练集，其他图像作测试集，充分测试40次求得平均识别率。MCVCF固定参数λ=0.6、C=1，MCLPVCF固定参数λ=0.6、C=1，训练集图像个数为5时固定参数k=2，t=0.5，为10、15、17时k=3，t=1.5，为20时k=4，t=1，MMCF、MMVCF和ZAMMCF固定参数λ=0.6、C=1，OTSDF固定参数λ=0.6。

AR数据集的实验结果如表4所示，可以看出，大部分情况下，所提两种算法都取得了最优和次优的平均识别率，在训练集图像数目增多的情况下，这种优势则更加明显。

表4 不同滤波器在AR数据集上的平均识别率及标准差（%）

从上述所有实验可以看出，无论是目标检测还是目标识别实验，MCVCF和MCLPVCF所取得的实验结果都比其他滤波器尤其是MMCF要更优秀，这说明在增加了对样本总体结构和内部结构信息的利用后，滤波器的构建和训练得到了优化，具体应用效果得到了提升。

4 结语

本文提出了两种基于数据分布信息的相关滤波器算法，所提算法可用于解决传统相关滤波器尤其是MMCF样本训练不充分的问题。本文在详细推导了算法模型和求解过程之后，进行了参数影响实验、人眼检测实验、物体和人脸识别实验，从实验结果可以看出，所提算法的检测准确率和平均识别率均取得了最优，证明了所提两种算法增加样本结构信息进行训练的有效性。