基于多参数融合优化的深度神经网络设计研究

蒋正锋，廖群丽

（1.广西民族师范学院数理与电子信息工程学院，崇左 532200；2.广西理工职业技术学院电子工程与智能化学院，崇左 532200）

0 引言

近年来，随着计算机技术的发展，深度学习（deep learning）在计算机视觉、自然语言处理和语音识别等多个领域［1］都已取得显著的效果，表现出极大的应用价值，现已成为人工智能的一个研究热点，并开创了神经网络发展的新纪元。

神经网络起源于1943年的McCulloch-Pitts（MCP）模型，是人工神经模型的最早的原型［2］。1985年感知器算法被提出来，使得MCP模型能对多维数据进行二分类处理，随后反向传播算法的提出为现代神经网络的快速发展打开了大门。20世纪80年代，启发卷积神经网络［3］和递归神经网络［4］相继被提出，而20世纪90年代，LeNet［5］应用于数字识别，取得了不错的效果。2006年，因深度神经网络理论在机器学习中取得初步成功的应用，Hinton等人提出了深度学习［6］的概念，引起了人们的关注。经过多年的发展，从单层网络逐渐发展到多层网络［7-8］，而多层的神经网络可能包含上百层以及上百兆的训练参数。2012年提出的深度学习架构AlexNet摘取了2012年视觉领域竞赛ILSVRC［9］（imageNet large-scale visual recogni⁃tion challenge）的桂冠，Top-5的错误率降低到15.3%［10］，其效果大幅度领先传统的方法。随后的几年，识别错误率不断被新提出更深层的卷积神经网络刷新，在2014年，VGGNet取得了89.3%的平均正确率［11］，2016年He等人提出的ResNet，将分类的错误率降低到3.57%［12］，而2017年由胡杰等人提出的SENet错误识别率只有2.25%。各种不同的深度神经网络模型的提出，促进了深度学习的发展。

深度学习的快速发展，离不开设计更加优秀的深度学习模型，人们也逐渐意识到深度学习模型的结构是深度学习研究的重中之重。深度学习的本质就是构建具有多个隐层的人工神经网络模型，人工神经网络的结构不管浅层还是深层主要是根据实验和经验来设计，但目前还没有一套具体理论可遵循。本文基于TensorFlow框架，采用一种先简单后复杂，多参数融合逐步优化的神经网络设计方法，为后续设计更复杂的深度神经网络提供了思路。

1 TensofFlow简介

Google公司在计算机相关的很多领域都有卓越的表现，人工智能领域也不例外。TensforFlow是Google公司2015年开发的基于DistBelief的一款优秀开源的深度学习框架，设计神经网络结构代码简洁，得到越来越多开发者的青睐。TensFlow不是全部由Python编写，很多底层代码是由C++或CUDA编写的，它提供Python和C++的编程接口，对线程和队列的基本运算能从底层来实现，也能较方便调用到硬件资源。用户借助Tensor⁃Flow灵活的架构，可部署到多种平台（CPU、GPU、TPU）进行分布式计算，为大数据分析提供支持。TensorFlow的跨平台性也好，在各种设备（桌面设备、服务器集群、移动设备、边缘设备）下工作。总之，TensorFlow为计算机视觉、自然语言处理和语音识别等机器学习和深度学习提供了强有力的支持，并且其灵活性的数值计算核心也可广泛应用于其他科学领域。

2 深度神经网络模型设计

构建一个神经网络模型，没有具体理论可遵，但与待解决的具体问题有关。以TensorFlow的经典实战项目MNIST手写数字识别为例，探索如何逐步设计一个满足要求的多参数融合的神经网络模型。设计任意一个浅度或深度的神经网络，一般来说按如下的4个步骤：①数据预处理。②构建符合要求的初步模型。③选择激活函数、损失函数和优化器。④训练模型和评价模型。

本文将详细讨论整个设计神经网络步骤中的各个环节。

2.1 数据的预处理

为了在训练中更加容易提取数据的相关信息，需要对数据进行预先处理。数据预处理包括归一化技术、非线性变换、特征提取、离散输入、目标编码、缺失数据的处理和数据集的划分等。数据集的划分根据评估模型方法验证和交叉验证来划分。模型方法为验证时，选择数据集后，一般会把数据划分为三个子集：训练集、验证集和测试集。训练集的大小占整个数据集的70%左右，用于构建预测模型，验证集占整个数据集的15%左右，评估训练阶段模型的性能，测试集也占整个数据集的15%左右，评估模型未来可能性的性能。

选择MNIST数据集，它是著名的手写体数字机器视觉数据集。两条途径获得MNIST数据集，一是从Yann LeCun教授的官网上下载，二是使用TensorFlow的官方案例，而MNIST数据集包含在TensorFlow中。MNIST数据集有60000个样本，其中55000个样本为训练集，另5000个样本为验证集的一部分，验证集总共10000个样本，还有5000个是从训练集中随机选择的，测试集样本数为10000。整个数据集的划分如表1所示。

在数据集MNIST中，每个样本包含了灰度值信息和这个样本对应的标签，每张图片样本都是28×28像素的手写数字组成，为了简化模型，通过降维处理，二维28×28的图片转化为有784个特征的一维向量，则训练集的特征为一个［55000，784］的张量，测试集和验证集的特征分别为［10000，784］和［10000，784］的张量。训练数据集对应的标签是一个［55000，10］的张量，其中第55000表示训练集中有55000张样本图片，10表示训练集中每张图片样本的标签是一个包含10个数字种类的one_hot编码。在实验中，用到训练集和测试集，训练集对神经网络进行训练，测试集验证设计的神经网络效果。

2.2 构建符合要求的初步模型

神经网络中输入层神经元的个数与数据集中样本的维度有关，而输出层神经元的个数与分类类别数量有关。MNIST数据集中样本是28×28二维的，转成一维向量有784个灰度值，决定神经网络模型的输入层中神经元的个数为784。MNIST数据集是手写体数字是0到9共10个分类，所以输出层神经元的个数为10。先设计一个没有隐含层的简单神经网络，即只有输入层和输出层，如图1所示。

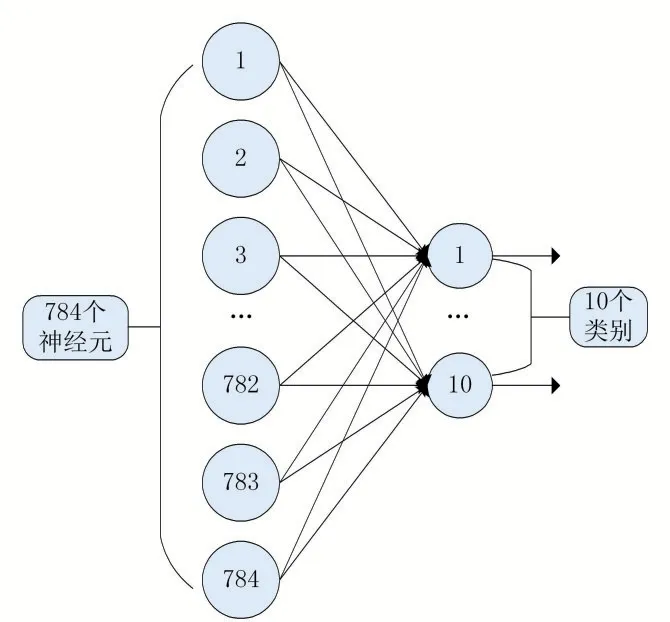
图1 没有隐含层的简单神经网络

无隐层神经网络输入层和输出层的神经元数量确定后，通过实验优化多参数融合的简单神经网络，然后在没有隐含层神经网络的基础上逐渐增加隐含层，隐层的层数以及每层神经元的个数通过多参数调优确定。

2.3 选择激活函数、损失函数和优化器

2.3.1 激活函数

激活函数是使神经网络具备了分层的非线性映射学习的能力，几乎可以逼近任意的函数，能解决更为复杂的问题。早期神经网络的激活函数有sigmoid函数或tanh函数，近年来在深度学习网络中应用relu函数比较多。如何选择激活函数，还没有一个确定的方法，主要还是凭一些经验。几个常用的激活函数如下：

（1）sigmoid函数。sigmoid是常用的非线性的一种激活函数，其定义如式（1）所示：

把输入z映射到0到1之间的范围，但在深度神经网络中sigmoid激活函数会导致梯度爆炸和梯度消失的问题，并且sigmoid函数的输出是非零均值信号作为下一层的输入，会导致收敛缓慢，并且sigmoid函数有幂运算，运算比较耗时等缺点。

（2）tanh函数。tanh函数解决了sigmoid函数的输出是非零均值信号作为下一层输入的问题，但梯度消失和幂运算问题在以tanh为激活函数的深度神经网络中依然存在。tanh函数的解析式如公式（2）所示。

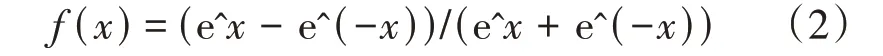
（3）relu函数。relu函数的解析式如公式（3）所示。

relu是一个分区间取最大值的函数，不是全区间可导的，但它解决了神经网络梯度消失的问题，只判断输入x与0的大小，计算速度非常快，收敛速度快于sigmoid和tanh激活函数。

2.3.2 损失函数

损失函数是估算设计的神经网络模型预测值ypre=f（x）与真实值yhat之间的差异，通常用L oss（yh at，ypre）来表示损失函数，常见的损失函数如下：

（1）0-1损失函数。0-1损失函数的定义如公式（4）所示。

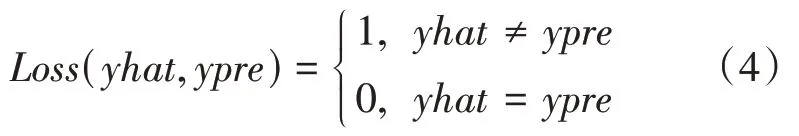
0-1损失函数不考虑预测值和真实值差异程度，如果预测正确，则损失函数的值为0，否则损失函数的值为1。

（2）平方损失函数。平方损失函数的定义如公式（5）所示。

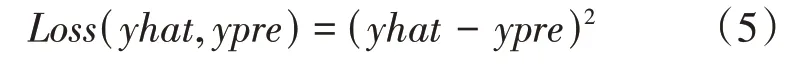
平方损失函数的值是预测值和真实值差异的平方。

（3）交叉熵损失函数。交叉熵是用来描述实际输出概率分布q（x）与期望输出概率p（x）的距离，交叉熵函数H（p，q）的定义如公式（6）所示。

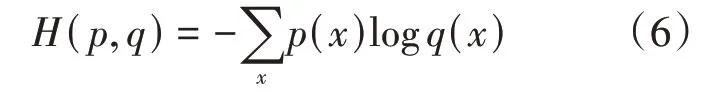
2.3.3 优化器

设计神经网络模型后，定义好损失函数，在训练模型时使损失函数随训练迭代次数的增加逐渐趋于0，这是优化器的作用。常用的优化器有梯度下降法（gradient descent）、动量优化法和自适应学习率优化算法等。

（1）梯度下降法。梯度下降法是最基本的优化器，主要分三种，即标准梯度下降法（gradient descent）、随机梯度下降（stochastic gradient de⁃scent）和批量梯度下降（batch gradient descent）。

（2）动量优化法。动量优化方法是基于梯度下降法，具有加速梯度下降的作用。一般有标准动量优化方法Momentum和NAG（nesterov acceler⁃ated gradient）动量优化方法。

（3）自适应学习率优化算法。传统优化器中学习率是常数或根据训练次数动态变化，没有考虑学习率其他变化的可能性，而学习率对模型的收敛有显著的影响，采取一些策略更新学习率，提高模型的训练速度。自适应学习率优化算法目前主要有AdaGrad算法、RMSProp算法、Adam算法和AdaDelta算法。

2.4 训练模型和评估模型

神经网络模型的参数是weight（权重）和bias（阈值），训练模型是通过训练样本和学习算法反复调整weight和bias模型参数值，使实际输出与理想输出的误差较少，最后得到神经网络解决问题所需要的参数。训练模型的学习算法中，最具有代表性的是误差反向传播（error backpropaga⁃tion，BP）算法，广泛应用于多层前馈神经网络。

评估模型的方法有验证和交叉验证，不同的评估方法也决定数据集的划分。分类问题常见的模型评价指标有混淆矩阵（confusion matrix）、准确率（accuracy）、精确率（precision）、召回率（recall）、特异度（specificity）等，如表2所示。

（1）混淆矩阵是一个N×N的矩阵，其中的N表示类别数量，混淆矩阵中的行表示样本的预测类别，列表示样本的真实类别。

（2）准确率是预测正确的样本数占所有样本数的比例。

（3）阳性预测值或精确率是阳性预测值被预测正确的比例。

（4）阴性预测值阴性预测值被预测正确的比例。

（5）召回率或灵敏度是在阳性值中实际被预测正确所占的比例。

（6）特异度在阴性值中实现被预测正确所占的比例。

表2中True Positive（TP）是被模型预测为正的正样本，False Positive（FP）是被模型预测为正的负样本，False Negative（FN）是被模型预测为负的正样本，True Negative（TN）是被模型预测为负的负样本。大多数情况下评估模型只用到准确率，根据具体的应用侧重于不同的评估指标。

表2 评估模型常见的指标

3 实验结果与分析

实验在Intel（R）Core（TM）i7-6700HQ CPU@2.6 GHz 2.59 GHz，8 GB内存的Windows 10系统上使用TensorFlow进行测试的。

3.1 简单神经网络设计

MNIST数据集中样本图片转成一维向量有784个元素，决定输入层神经元的个数为784，而手写体数字共10个类别，则输出层神经元的个数为10。无隐层简单的神经网络，只有输入层和输出层，层与层之间采用全连接方式。

（1）损失函数的比较。学习率设置为0.1，训练模型样本批次大小是100，迭代次数为30，优化器采用梯度下降法，比较交叉熵和平方损失函数作用于简单神经网络的识别准确率。

图2（a）是训练模型迭代次数与准确率之间的曲线关系，其中上边两条曲线为一组，是损失函数为交叉熵时训练集和测试集的准确率曲线，下边两条曲线是损失函数为平方损失函数时训练集和测试集的准确率曲线。由图2（a）可知，在任何迭代次数上，损失函数为交叉熵时训练集和测试集的准确率都大于损失函数为平方损失函数时训练集和测试集的准确率。图2（b）是迭代次数与损失值的曲线关系，同样也分两组，损失值高的一组是损失函数为平方损失函数时训练集和测试集的损失值曲线，损失值低的一组是损失函数为交叉熵时训练集和测试集的损失值曲线，图2（b）可知，损失函数为交叉熵时收敛速度快。由图2交叉熵与平方损失函数准确率和损失值的比较可知，选择交叉熵作为简单神经网络的损失函数。

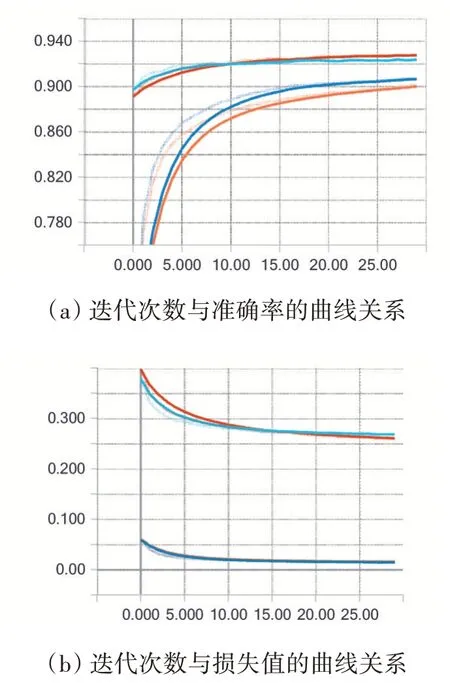
图2 交叉熵与平方损失函数的比较

（2）不同学习率。训练模型样本批次大小是100，迭代次数为30，优化器采用梯度下降法，损失函数为交叉熵，比较不同学习率（0.1、0.2、0.3、0.4、0.5、0.6）对神经网络模型的影响。

图3展示了基于不同学习率准确率的对比，上一行是训练集的测试结果，下一行是测试集的测试结果。

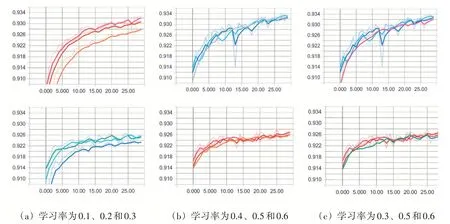
图3 不同学习率对神经网络准确率的影响

图3（a）展示学习率分别为0.1、0.2和0.3时准确率随迭代次数变化的三条曲线。实验结果表明，随着学习率的增加，神经网络的性能逐步改善，在训练集和测试集中，学习率为0.3时准确率几乎都是最高的，迭代次数为30准确率分别为93.30%和92.58%。图3（b）是学习率分别为0.4、0.5和0.6时准确率随迭代次数变化的曲线。实验结果表明，训练集中学习率为0.5和0.6时准确率波动较大，特别是学习率为0.5准确率不稳定。迭代次数为30时，学习率0.6训练集准确率最高，学习率0.5测试集准确率最高。图3（c）是学习率分别为0.3、0.5和0.6时准确率随迭代次数变化的曲线。实验结果表明，不管是训练集还是测试集，不同学习率的准确率相差不大，学习率0.5和0.6的准确率比学习率0.3的准确率稍高，但训练集中学习率0.5和0.6的准确率波动较大。由图3分析可知，学习率0.3到0.4之间比较合适，所以学习率选择0.3。

（3）批次大小。学习率为0.3，迭代次数为30，优化器采用梯度下降法，损失函数为交叉熵，比较不同批次大小（50、100、150、200、250、300）对神经网络模型的影响。

图4展示不同批次大小准确率的对比，上一行是训练集在不同批次大小的测试结果，下一行是测试集在不同批次大小的测试结果。图4（a）是批次大小分别为50、100和150时准确率随迭代次数的三条曲线。实验结果表明，训练集中，批次大小为50的准确率高于批次大小为100和150的准确率，而测试集中，批次大小为100的准确率高于批次大小为50和150的准确率。图4（b）表示批次大小分别为200、250和300时准确率随迭代次数的曲线关系，训练集中，迭代次数30批次大小200时准确率为93.03%，高于批次大小250和300对应的准确率92.89%和92.85%，而测试集中迭代次数30批次大小200时准确率也是最高的。图4（c）表示批次大小分别为100、200和300时准确率随迭代次数的曲线关系，不管是训练集还是测试集，批次大小100时准确率最高。由图4分析可知，批次大小为100模型的性能最好。

图4 不同批次大小对神经网络准确率的影响

（4）优化器的选择。训练模型样本批次大小是100，迭代次数为30，损失函数为交叉熵，学习率为0.3，比较不同优化器（梯度下降、Adam算法、AdaDelta算法和AdaGrad算法）对神经网络模型的影响。图5展示不同优化器在训练集和测试集上的准确率曲线，图5（a）表示的是梯度下降、Adam算法、AdaDelta算法和AdaGrad算法在训练集中准确率随迭代次数增加的变化曲线，最上边的两条准确率曲线对应的优化器是梯度下降和AdaGrad。实验结果表明，梯度下降和AdaGrad的性能优化Adam和AdaDelta算法，而AdaGrad算法的性能最优。图5（b）与图5（a）是对应的，曲线的长度表示准确率的范围，灰色曲线表示AdaGrad算法所对应的准确率。图5（c）表示在测试集中，不同优化器的准确率随迭代次数增加的变化曲线，实验结果表明，最上边的两条准确率曲线对应的优化器是梯度下降和AdaGrad，而AdaGrad算法的性能最优。由图5分析可知，优化器选择AdaGrad算法。

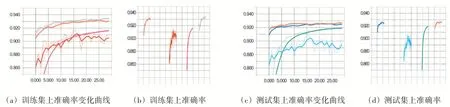
图5 不同优化器在训练集和测试集上准确率随迭代次数的变化曲线

以上所有实验结果分析表明，设计无隐层多参数融合具有较高准确率的简单神经网络，可参考表3所示多个参数及对应的值。

表3 无隐层的简单神经网络参数

3.2 单层隐含层神经网络设计

在无隐层多参数融合优化的简单神经网络基础上通过增加一隐层继续提高准确率，需考虑的是隐层神经元的个数、激活函数及迭代次数等方面。

（1）隐层神经元的个数。样本批次大小100，迭代次数30，损失函数为交叉熵，学习率0.3，优化器是AdaGrad算法，激活函数sigmoid，单层隐含层，比较隐层不同数量神经元对神经网络模型的影响。

图6展示了单隐层不同数量神经元在训练集和测试集中准确率随迭代次数变化的曲线，每幅图中6条曲线在迭代10次后明显分成两组，每组3条曲线几乎重合在一起。实验结果表明，单隐层神经网络在训练集的准确率高于在测试集的准确率，隐层不同神经元个数对神经网络模型的性能影响不大，如训练神经网络模型迭代25次时，图6（a）神经元个数为400、500和600在测试集中对应的准确率分别为98.04%，98.07%和98.10%，在训练集中对应的准确率分别为99.85%，99.83%和99.85%，准确率非常接近。图6（b）和图6（c）与图6（a）类似，隐层不同神经元的个数对准确率影响不大，所以选择隐层神经元个数为500。

图6 隐层不同神经元个数对识别准确率的影响

（2）激活函数。样本批次大小100，迭代次数30，损失函数为交叉熵，学习率0.3，优化器是AdaGrad算法，单隐层神经元个数为500，比较不同激活函数（sigmoid、tanh、rule和selu）对神经网络模型的影响。

图7展示不同激活函数准确率的对比，上一行是训练集上不同激活函数的测试结果，下一行是测试集上不同激活函数的测试结果。图7（a）表示激活函数sigmoid和tanh在训练集和测试集中准确率随迭代次数变化的曲线。实验结果表明不管在训练集还是测试集中使用tanh激活函数比使用sigmoid激活函数效果好。图7（a）上图展示迭代16次以后，使用tanh激活函数的准确率为100%，而使用sigmoid激活的准确率在99.30%～99.99%之间。图7（b）表示激活函数relu和selu在训练集和测试集中准确率随迭代次数变化的曲线。实验结果表明，测试集中使用relu激活函数比使用selu激活函数效果好,训练集中迭代20次前使用relu激活函数比使用selu激活函数效果好，迭代20次以后使用relu和selu激活函数的准确率都为100%。图7（c）是四种激活函数在训练集和测试集中准确率随迭代次数变化的曲线，训练集中使用relu激活函数准确率在迭代12次达到了100%，测试集中使用relu激活函数的准确率比使用其他三种激活函数的准确率高。

图7 不同激活函数对识别准确率的影响

以上单隐层所有实验结果分析表明，设计单隐层多参数融合具有较高准确率的神经网络，需确定隐层神经元的个数、隐层的激活函数、学习率、优化算法等参数参考表4所示。

表4 单隐层的神经网络模型参数

3.3 多层隐含层神经网络设计

在多参数融合优化的单隐含层神经网络的基础上再增加一隐层，继续优化神经网络模型。样本批次大小100，迭代次数30，损失函数为交叉熵，优化器是AdaGrad算法，两层隐含层，隐含层神经元的个数分别为500和300，隐含层的激活函数是relu，在测试集中比较不同学习率（0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5、0.55、0.6、0.65、0.7）对神经网络模型的影响。

由表5可知，学习率为0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45时的准确率高于学习率为0.5、0.55、0.6、0.65、0.7。学习率为0.1、0.15、0.2、0.25、0.3、0.35、0.4的准确率相差不大，它们的准确率随迭代次数的变化曲线几乎是重叠在一起，其中学习率0.2和0.25的性能最优。实验结果表明，多层隐含层神经网络的学习率设定为0.2。

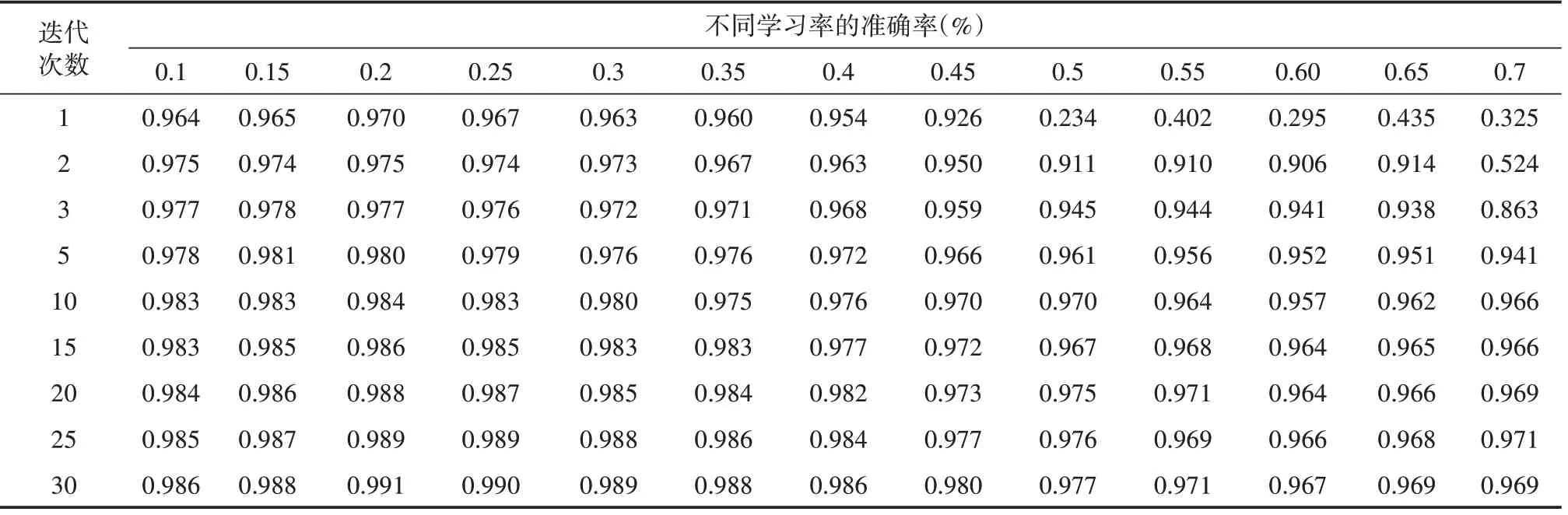
表5 测试集中不同学习率

样本批次大小100，迭代次数30，损失函数为交叉熵，学习率为0.2，优化器是AdaGrad算法，两层隐含层，隐含层神经元的个数分别为500和300，在测试集中比较隐含层不同激活函数（sigmoid、relu、selu和tanh）对神经网络模型的影响。图8展示了使用不同激活函数在测试集上准确率的对比，上一行是不同激活函数在训练集上准确率的测试结果，下一行是上一行对应损失函数随迭代次数的收敛曲线。图8（a）是激活函数sigmoid与relu准确率和损失函数值的对比，由上图中的曲线可知，使用激活函数relu的准确率高于使用激活函数sigmoid的准确率，下图中使用激活函数relu的多参数融合神经网络模型的损失函数随迭代次数增加收敛的比较快。

图8 不同激活函数对识别准确率的影响

图8（b）是激活函数selu与tanh准确率和损失函数值的对比，使用激活函数tanh的准确率比较高及损失函数收敛比较快。图8（c）是激活函数sigmoid、relu、selu和tanh准确率和损失函数值的对比。实验结果表明，使用激活函数relu和tanh的多参数融合神经网络模型性能比较好，而使用激活函数relu的神经网络模型的性能最好，所以选择relu作为激活函数。

不同激活函数在测试集中准确率随迭代次数的如表6所示。

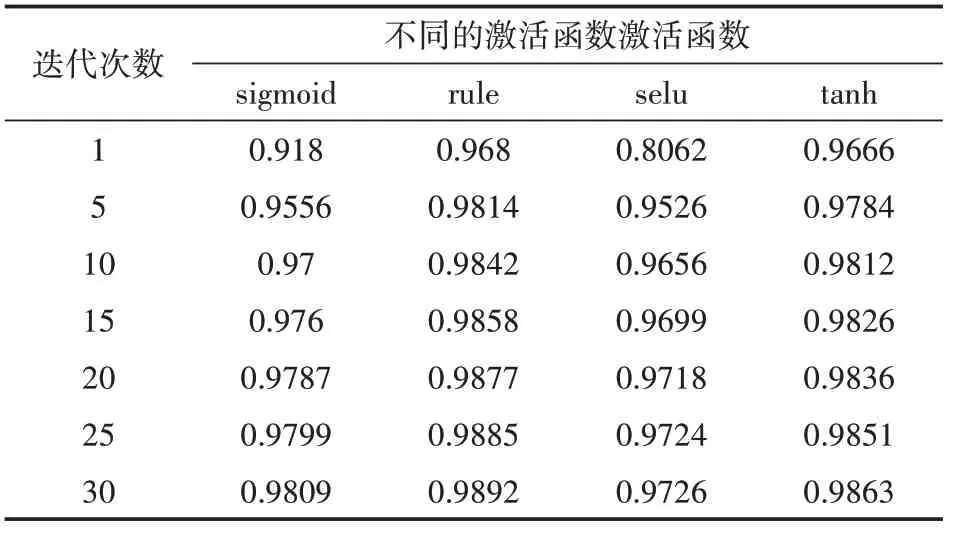
表6 测试集中不同激活函数

样本批次大小100，迭代次数30，学习率为0.2，优化器是AdaGrad算法，两层隐含层，隐含层神经元的个数分别为500和300，隐含层的激活函数是relu，比较不同损失函数（平方损失函数和交叉熵）对模型的影响。图9主要展示了使用不同损失函数在训练集和测试集上准确率的对比，上一行是不同损失函数准确率的测试结果，下一行是上一行对应损失函数随迭代次数的收敛曲线。上图和下图对比发现，识别准确率高的曲线对应的损失函数收敛的速度就快。图9（a）上图是在训练集中分别使用平方损失函数和交叉熵时神经网络模型的识别准确率曲线，由图中两条曲线对比可知，神经网络的损失函数为交叉熵优于平方损失函数，在训练使用交叉熵的神经网络模型迭代10次后训练集中的识别准确率达到了100%，其对应的10（a）下图损失值也快速收敛。图9（b）上图是测试集中分别使用平方损失函数和交叉熵时神经网络模型的识别准确率曲线，其中损失函数是交叉熵的神经网络模型的识别准确率高的。图9（c）是平方损失函数和交叉熵在训练集和测试集上的识别准确率曲线以及对应的损失函数的收敛曲线。实验结果表明，在训练集和测试集上损失函数是交叉熵都优于平方损失函数的多参数融合神经网络模型的性能。

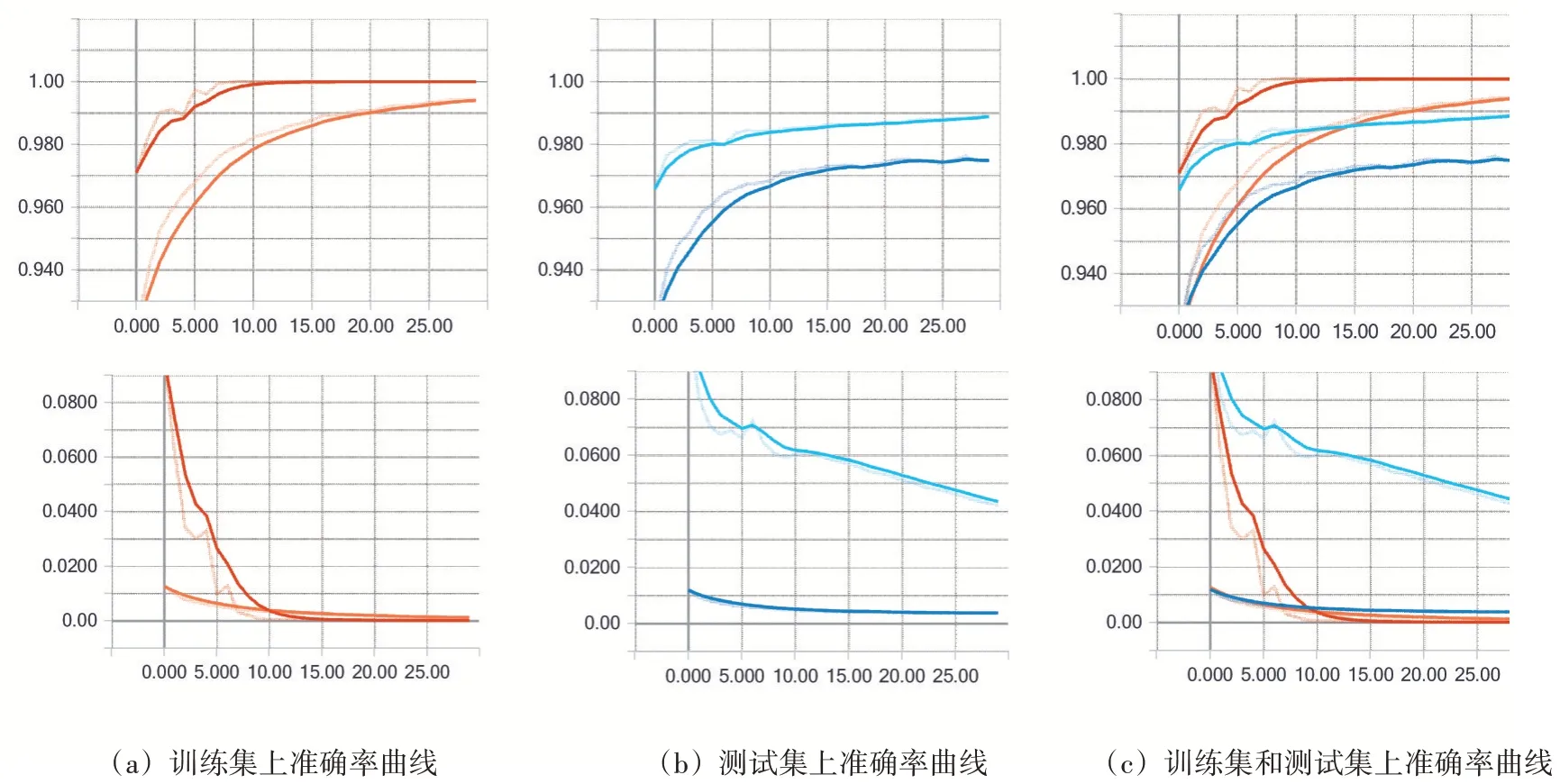
图9 不同损失函数对识别准确率的影响

样本批次大小100，迭代次数30，学习率为0.2，损失函数为交叉熵，两层隐含层，隐含层神经元的个数分别为500和300，隐含层的激活函数是relu，比较不同优化算法（梯度下降、Adam算法、AdaDelta算法和AdaGrad算法）对模型的影响。图10展示了不同优化算法的对比，上一行是梯度下降、AdaDelta算法和AdaGrad算法在训练集和测试集上识别准确率随迭代次数增加的变化曲线，下一行是上一行不同优化算法对应交叉熵的收敛曲线。图10（a）上图是梯度下降、AdaDelta算法和AdaGrad算法在训练集的识别准确率变化曲线，其中梯度下降和AdaGrad优化算法对应的准确率变化曲线在迭代5次时准确率都就到达了99%以上，并且AdaGrad优化算法稍微优于梯度下降优化算法，而AdaDelta优化算法对应的准确率变化曲线低于梯度下降和AdaGrad优化算法对应的准确率变化曲线。图10（b）上图是梯度下降、AdaDelta算法和AdaGrad算法在测试集的识别准确率变化曲线，在训练迭代3次后，识别准确率从高到低所对应的优化算法分别为AdaGrad算法、梯度下降优化算法和AdaDelta算法，迭代30次AdaGrad优化算法对应的准确率为98.90%。图10实验结果表明，AdaGrad算法的性能最优。

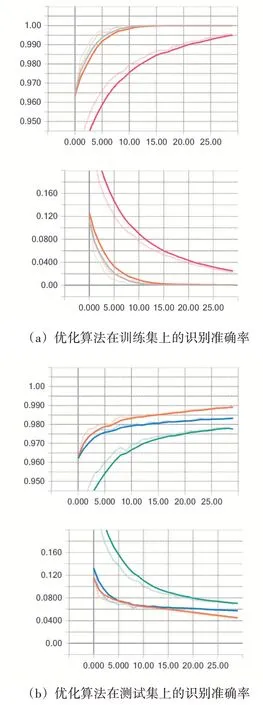
图10 优化算法在训练集和测试集上对识别准确率的影响

综合以上多隐层实验结果表明，设计多隐层多参数融合优化具有较高准确率的神经网络模型，隐层神经元个数、隐层的激活函数、优化算法、学习率、损失函数等参数可参考表7所示。

表7 多隐层神经网络模型参数

4 结语

深度学习是目前最火热的研究方向之一，它借助于计算机强大的计算和存储能力进行快速搜索而完成对样本的特征提取，同时缺乏对网络结构及参数在理论上的完全解释，所以结合领域知识的特征提取，设计多参数融合优化的深度神经网络是深度学习发展的一个方向。本文讨论了在无隐层神经网络模型的基础上逐渐怎样设计出一个多参数融合优化的具有较高准确率的深度神经网络模型，特别是为初学者构建深度神经网络模型提供了一种有效思路，也为以后在经典深度神经网络模型的基础上设计更复杂的神经网络打下基础。