具有随机收入和扩散干扰的相型风险模型的 期望折现罚函数
黎 琴
(菲律宾圣保罗大学 工商管理学院,菲律宾 土格加劳 3500)
1 模型与假设
在保险数学研究中,许多文献假设索赔到达时间的间距服从phase-type 分布,因为phase-type 分布包括了指数分布、超指数分布、Erlang(n)分布等,因此,研究这类更新风险模型,可以得到具有更一般性的结论.文[1]研究索赔到达时间间距服从phase-type 分布风险模型中的期望折现罚函数,文[2]推广了文[1]中的风险模型,考虑两类索赔风险模型的期望折现罚函数.文[3]基于文[2]提出的风险模型,研究直到破产时的总红利支付问题.文[4]探索带扩散干扰多阈值两类索赔更新风险模型,当两类索赔到达时间间距均服从phase-type 分布时,得到期望折现罚函数的相关性质.这些文献都假设单位时间年金收入率为一个常数或为阶梯函数.
近年来,随机年金收入的保险风险模型研究得到广泛的关注.文[5]假设年金收入到达过程为Poisson过程时,研究索赔过程为复合Poisson 过程风险模型中的期望折现罚函数.文[6]考虑索赔数量与索赔到达过程具有相依关系时的期望折现罚函数.
本文在文[7]研究的具有随机收入的更新风险模型中引入扩散干扰项,在索赔到达时间间距服从phase-type 分布时,探索期望折现罚函数和破产概率的相关性质.
考虑具有随机年金收入和扩散干扰的保险风险模型
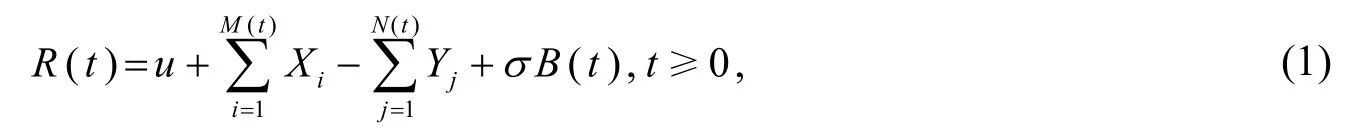
其中u≥ 0为初始资本; {M(t);t≥ 0}是参数为λ> 0的Poisson 过程,表示到时刻t时的年金收入次数; {Xi;i≥ 1}是独立同分布的随机变量序列,表示第i次的年金收入数量,其分布函数为F(x),x≥ 0,且概率密度函数f(x)=F′(x),Laplace 变换表示到时刻t时的索赔到达次数; {Yi;i≥ 1}是独立同分布的随机变量序列,表示第i次的索赔数量,其分布函数为且概率密度函数g(x)=G′(x)以及Laplace 变换{B(t);t≥ 0}为标准的布朗运动;σ> 0表示扩散系数.设{M(t);t≥ 0},{N(t);t≥ 0},{Xi;i≥ 1},{Yi;i≥ 1}和{B(t);t≥ 0}相互独立.索赔到达时间间距Ti(i=1,2,… )的分布函数K(t)服从PH(α,A)分布,其中是n×n矩阵,满足aii< 0,当i≠j时,aij≥ 0和且a=-Aen,en是分量均为1 的n维列向量,eT是e的转置,I表示单位矩阵.由文[8]可知,K(t) = 1-αTeAten,t≥ 0;k(t)=αTeAta,t≥ 0和
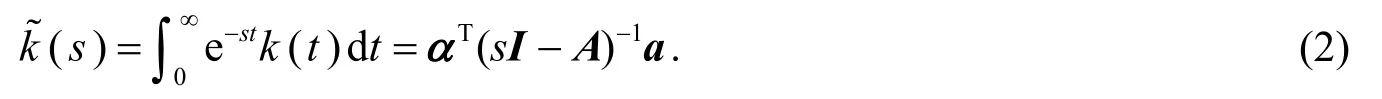
根据phase-type 分布的定义,索赔时间间距Ti(i=1,2,… )对应于终止连续时间Markov 链到达吸收状态时间,其中有n个瞬时状态{S1,S2,…,Sn}和一个吸收态{S0}.
定义最终破产时间τ=inf{t|R(t) ≤ 0},若对任意t≥ 0都有R(t) > 0,则τ=∞.R(τ- )表示破产前瞬时盈余,| R(τ)|为破产时赤字.破产概频
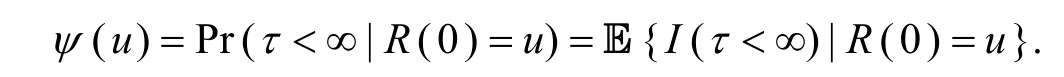
I(E)为集E的示性函数,即期望折现罚函数
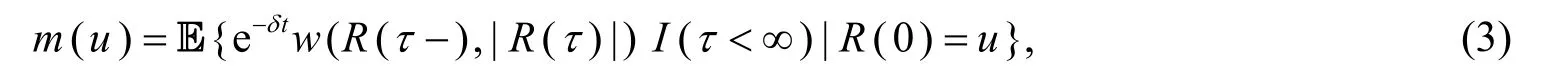
其中δ≥ 0,w(x1,x2)是一个非负函数,定义域为[0,∞ ) ×[0,∞ ).
设mi(u)表示R(0)=u,时的期望折现罚函数,即
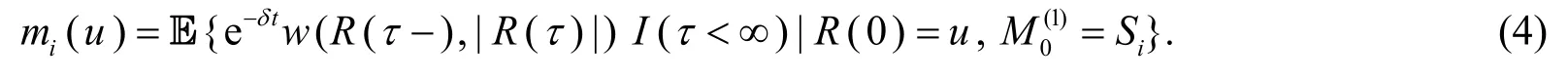
因此,有

其中m(u) ≡(m1(u),m2(u),… ,mn(u))T.
2 m(u)满足的积分-微分方程
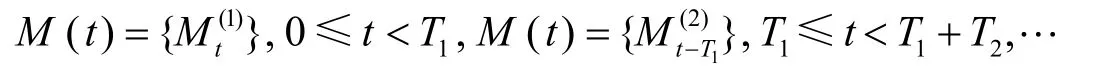
考虑极小的时间区间(0,)ε,易知,有且仅有下列五种情况发生: (1)没有收入到达也没有状态转移; (2)有一次收入到达且没有状态转移; (3)有一次状态转移但没有发生索赔且没有一次收入到达; (4)有一次索赔发生但没有一次收入到达; (5)两次或以上事件发生.因此
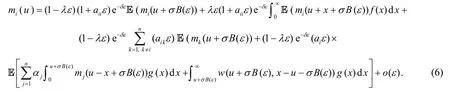
利用Itó公式
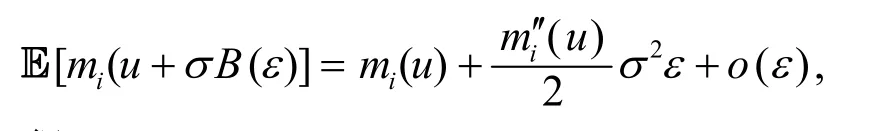
对式(6)进行整理,并令ε→0 ,得
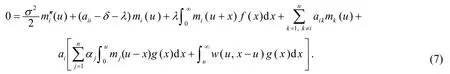
式(7)可以重写为
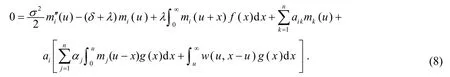
将式(8)写成矩阵的形式,可得到下面结论:
定理1期望折现罚函数向量m(u)满足积分-微分方程
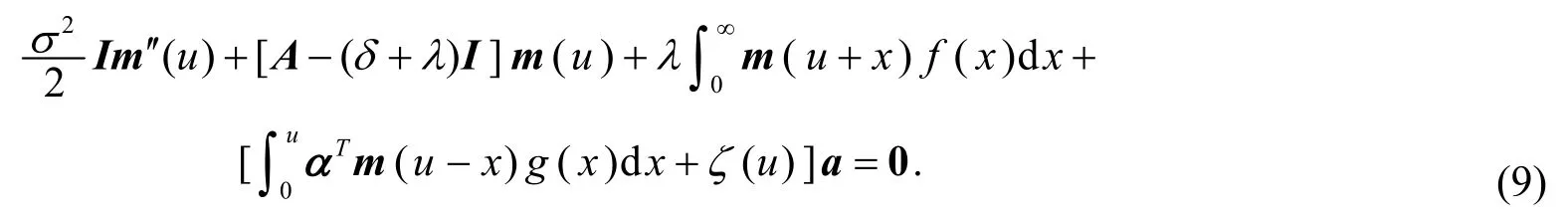
注1当σ= 0时,上式即为文[7]中的式(2.4).
注2当索赔到达过程为超指数分布时,即

由定理1,可得
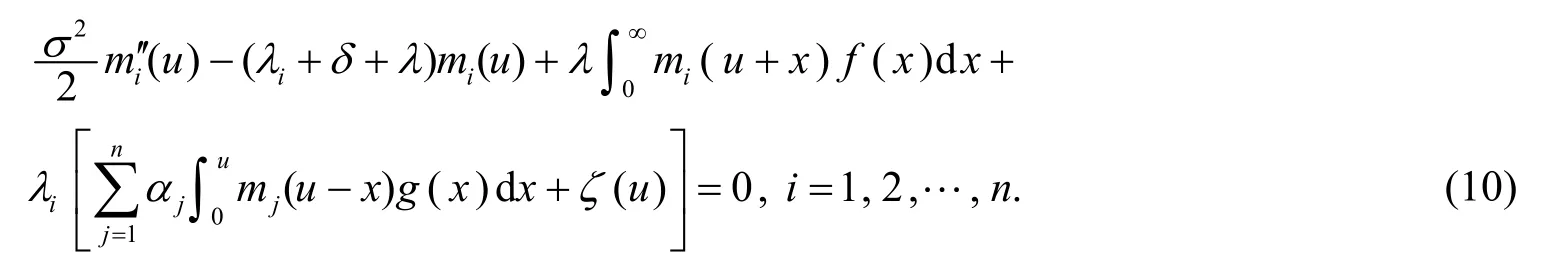
注3当索赔到达过程为广义Erlang(n)分布时,此时

由定理1 容易推出
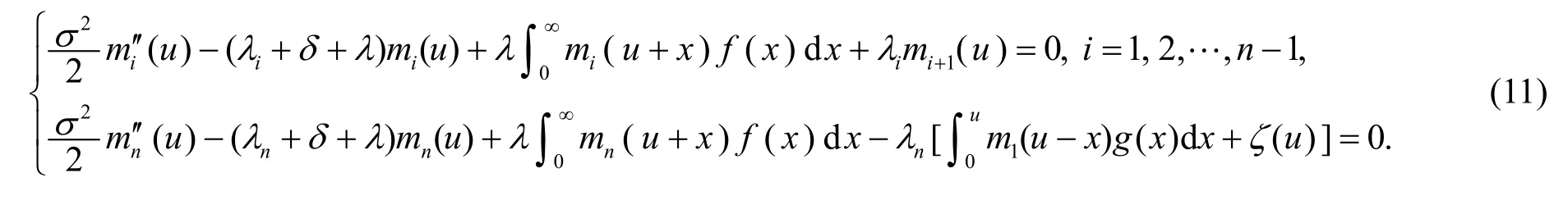
3 年金收入量服从超指数分布
假设年金收入量服从超指数分布,即

其中β1<β2< …<βn,Gi> 0,且G1+G2+ …+Gn=1,则分布函数
定义算子Tr,
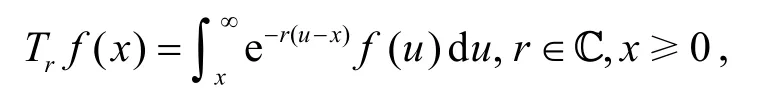
其中 ℜ(r) ≥0.容易验证: (1)即为f的拉普拉斯变换; (2)TrTsf(x)=算子Tr的其它性质可参考文[9].
注意到,对i=1,2,…,n,s≠βj,j=1,2,… ,n有
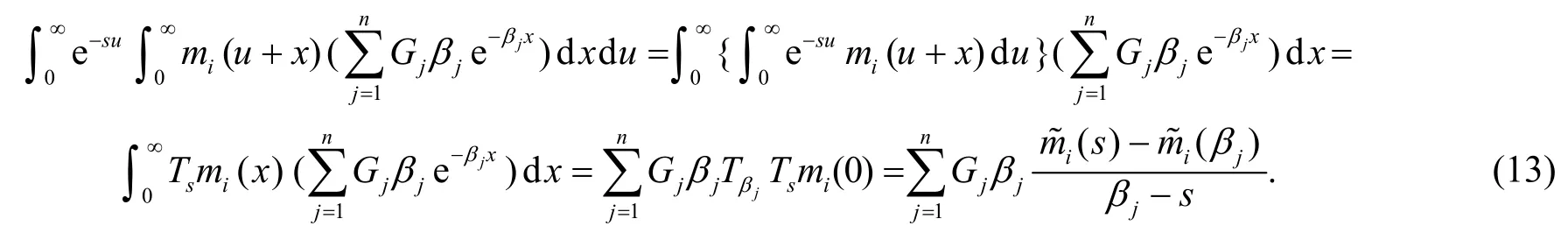
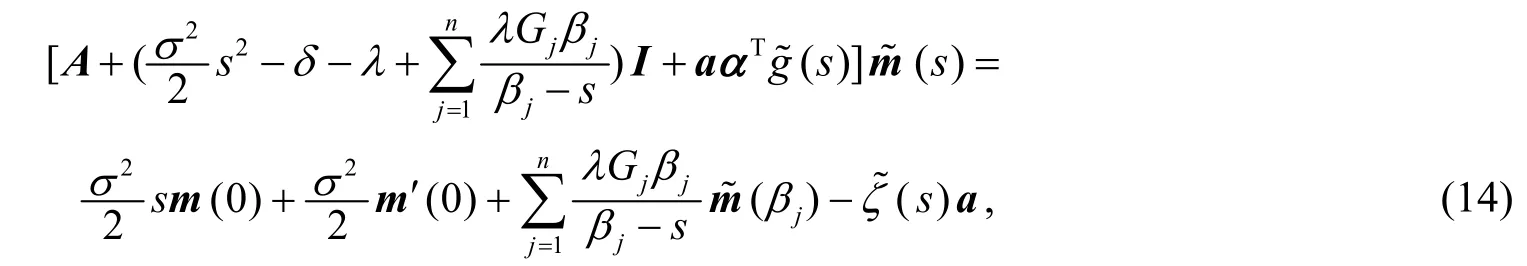
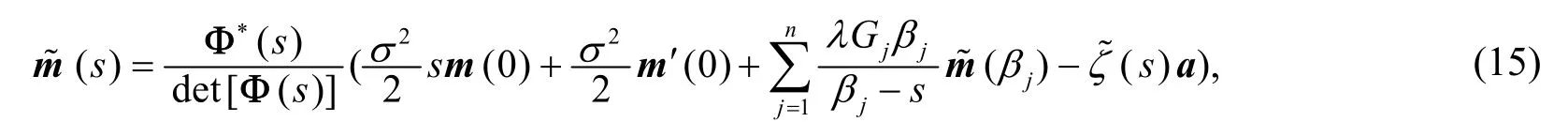
其中 Φ*(s)表示 Φ(s)的伴随矩阵.
由文[5],利用Rouché定理,当δ> 0时,推广的Lundberg 方程det[ Φ(s)] =0恰好有n个实部大于0的根,不妨设为ρ1,ρ2,…,ρn.当δ→ 0+时,则ρi(δ)→ρi(0),i=1,2,… ,n,且s= 0为Lundberg 方程det[ Φ(s)] =0的一个根.为简单起见,下面假设ρ1,ρ2,… ,ρn各不相同.

当设定初值条件m(0),m′ (0)时,由式(16),可解得
为了进一步的推导,首先引入矩阵差商的定义.矩阵 Φ(s)关于不同的数r1,r2,…的差商为
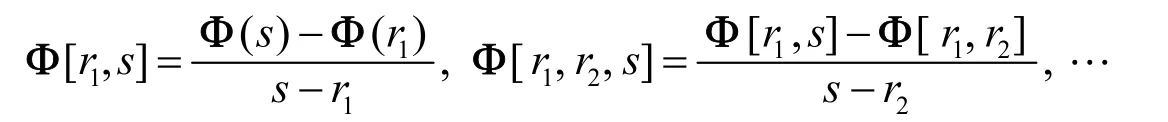
由式(16),有
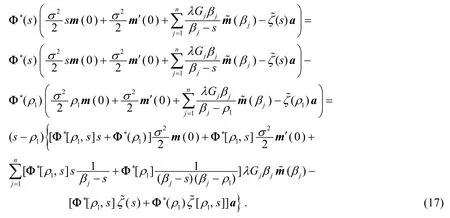
同时,由于s=ρ2是式(17)最后一个等式大括号内式子的一个零点,因此

当i= 1时,Φ*[ρ1,ρi]=Φ*(ρ1).将上式代入式(17),由s=ρ3,ρ4,… ,ρn也是式(15)分子的根,可得如下结论:
定理2期望折现罚函数的拉普拉斯变换为
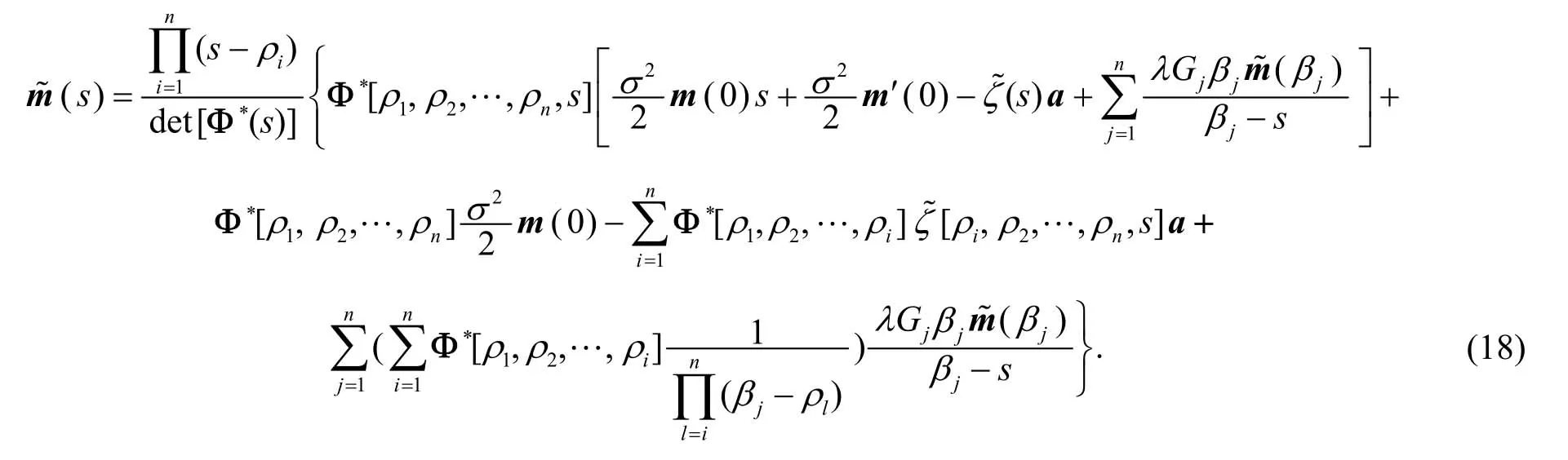
当索赔数量分布函数 ( )G x为有理分布函数族,即其拉普拉斯变换为有理分式时,利用文[7]的相似推导,可以得到期望折现罚函数的显式解.

