6016铝合金板成形极限NADDRG模型优化及验证

王彦东,钟 娟,史丹丹,郭新汝,申晓丽,赵志国

(1. 航鑫材料科技有限公司，山东 烟台 265706；2. 国家压力加工工程技术研究中心，山东 烟台 265713)

进入21世纪以来，机动车产业发展迅速，环境污染和能源短缺问题日益严重，轻量化已是汽车发展的必然趋势。当前主流的轻量化方法是采用轻量化材料，其中又以铝合金材料为主。6016铝合金综合性能较好，在汽车车身覆盖件应用广泛，其成形性能一直是研究的热点[1]。成形极限曲线(Forming Limit Curves，简称FLC)，是材料在不同应变路径下的极限应变描绘在以主应变和次应变为横纵轴的坐标轴中得到的，在冲压成形领域有着重要的应用。成形极限图可分为三个区域：曲线下方对应安全区域，曲线上方对应着破裂区域，曲线附近为极限区域。获得FLC最常用的方法是通过板材成形测试，通常受限于设备以及测试比较复杂，所以国内外很多学者致力于通过理论计算的方式得到FLC。由于理论计算得到曲线通常与实际生产应用有较大的差距，本文作者使用目前比较常用的NADDRG模型以及6016铝合金板，对产生差距的原因进行了应变路径提取分析，并对理论模型进行修改验证。

1 试样制备与测试

1.1 拉伸性能测试

试验材料为汽车用6016铝合金板，厚度为1.2 mm，制成图1所示拉伸试样，用INSTRON电子万能试验机对试样进行拉伸测试，拉伸性能见表1。

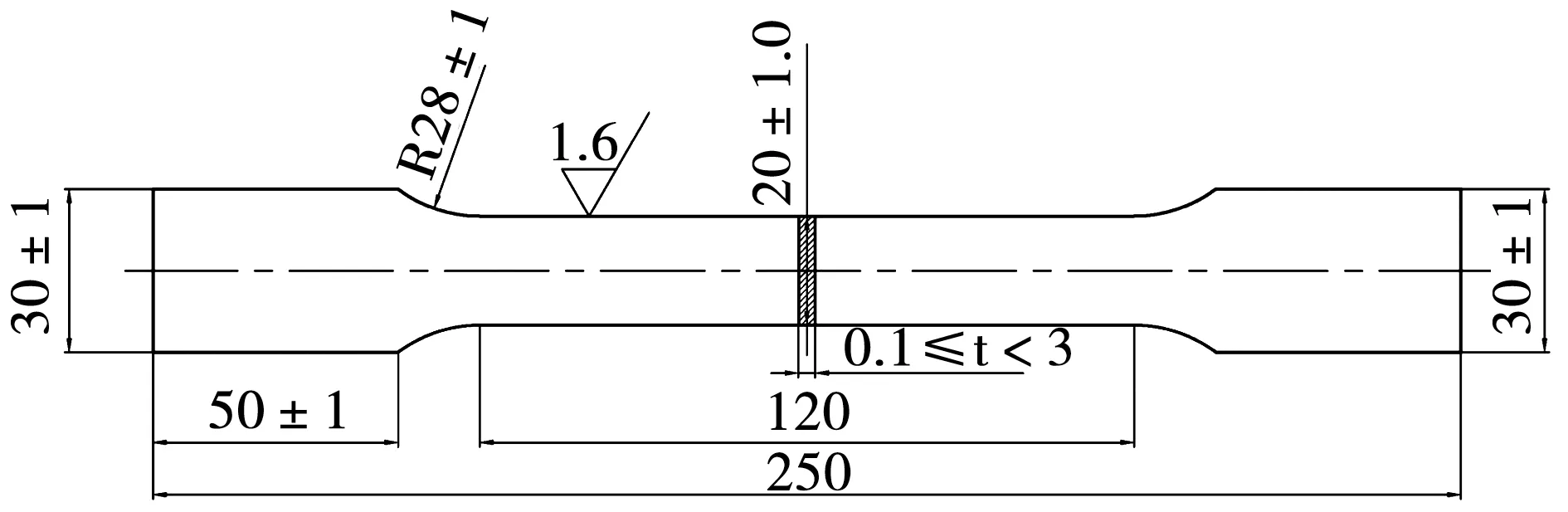
图1 拉伸测试板状试样(尺寸单位：mm)

表1 拉伸测试数据

1.2 成形极限曲线测试

采用Nakajima测试法对6016铝合金汽车板进行了成形极限曲线测试，通过不同宽度的试样得到不同应变路径下的极限应变。试样形状如图2所示。试样尺寸设置见表2。试验设备为德国Zwick公司生产型号BUP600的板材成形试验机，配备德国Gom公司生产的ARAMIS 3D 5M三维应变测量分析系统。

表2 成形极限曲线测试试样尺寸设置

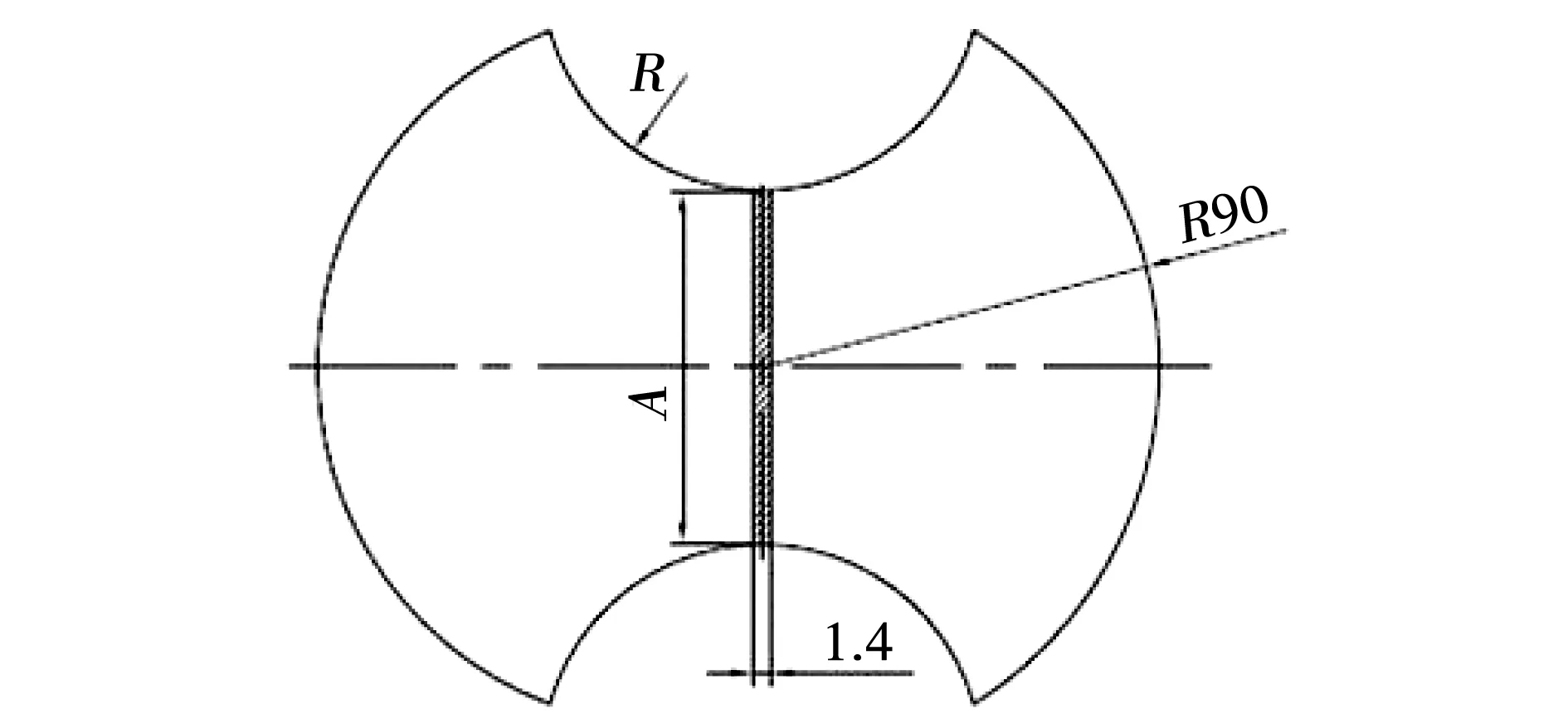
图2 成形极限曲线测试试样(尺寸单位：mm)

为获得测试过程中的应变情况，FLC试样在测试前需进行喷漆处理获得特征散斑。将晾干的试样放置在试验机压边圈之间，施加压边力，保证材料不会在试验过程中流入凹模内。启动设备后试样在凸模冲压力的作用下发生胀形变形，其表面的散斑发生畸变，当试样表面发生局部失稳产生破裂时即停止试验。三维应变测量分析系统对测试全程进行图像采集，最后根据存储在计算机上的图像采用软件完成应变计算分析工作，采用破裂或颈缩前应变截面线进行最佳反抛物线拟合找出极限应变值，描绘在坐标轴中，即得到材料的成形极限图。

2 NADDRG理论模型

因受限于设备以及成形极限曲线测试非常繁琐，得到一条曲线通常需要进行大量的试验，所以人们希望通过塑性理论，利用简单的力学性能推导出材料的成形极限。理论预测成形极限的方法从根本上说就是根据拉伸失稳理论判断板料最大成形能力的方法。1952年Hill和Swift分别提出分散性失稳和集中性失稳理论，阐述了两种失稳的力学模型，为以后塑性失稳理论的发展奠定了基础。但是基于连续性假设的材料在等双拉状态下不可能对其进行预测，所以在1967年Marciniak和Kuczynski提出了著名凹槽理论，通常简称M-K理论。后来，陈光南等通过对板料拉伸过程中表面损伤和内部损伤的研究，提出了平面应变漂移失稳准则，简称C-H准则[2-3]。北美拉深组织提出了一种可简单预测材料成形极限曲线的模型—NADDRG模型，根据该理论，当ε2=0时：

ε1=(23.3+360t/25.4)×n/0.21

(1)

式中：

ε1—主应变；

ε2—次应变；

t—材料厚度；

n—材料应变硬化指数。

当确定平面应变点(0，ε1)后，通过该点引两条直线，其中一条与坐标系横轴负方向成45°夹角，另一条与坐标轴正方向成20°夹角，得到曲线即为理论预测材料的成形极限曲线[4-5]。

3 结果与讨论

3.1 成形极限曲线测试与NADDRG模型预测对比

图3为6016铝合金板在室温条件下试验测得成形极限曲线(geometry strain)与运用NADDRG模型计算出的预测曲线。由图3可以看出，模型预测6016铝合金板材成形极限曲线结果比较接近实际测试，但实际检测结果中平面应变点并不是曲线的最低点，最低点要明显往右偏移，其主应变与理论预测平面应变点的主应变基本一致。

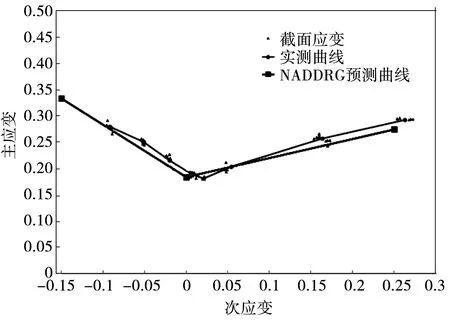
图3 实测成形极限曲线与NADDRG模型预测曲线

3.2 曲线最低点应变路径分析

通过分析将曲线最低点的试样在变形过程中不同时刻的应变放到坐标轴中，得到该试样从试验开始到破裂时的应变路径(如图4)。从图4可以看出，应变路径并不是完全平行于纵轴的线段，而是大致分为两部分：第一部分主应变和次应变同步增加，应变路径与坐标横轴正方向呈约45°夹角，这是因为球形凸模在行进过程中刚接触试样时，变形状态接近于等双向拉伸，此时主次应变基本相等；第二部分随着凸模和试样继续接触，次应变基本保持不变，主应变增加，直至达到极限应变，试样发生破裂。

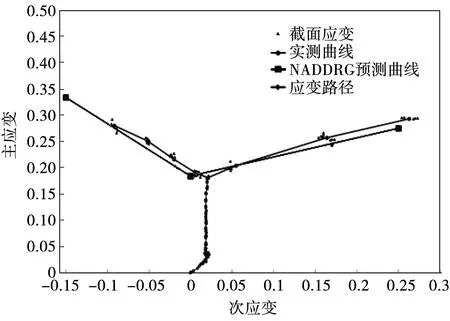
图4 曲线最低点应变路径

3.3 NADDRG模型改进

3.3.1 提出修改模型

笔者采用Nakajima法，润滑方式为硅胶垫加白凡士林，对6016铝合金板进行大量测试发现，通过试验得到的成形极限曲线最低点相较于NADDRG预测曲线次应变普遍向右偏移0.02左右，故对NADDRG模型进行修改，让预测结果更接近实际测试结果。修改后模型如下，当ε2=0.02时：

ε1=log[1+(23.3+360t/25.4)×n/0.21]

(2)

3.3.2 试验验证

为验证修改后NADDRG模型预测结果的准确性，笔者采用不同厚度的6016铝合金板进行成形极限曲线测试，将材料实测成形极限曲线与预测曲线描绘在坐标系中进行对比分析，图5为不同厚度6016铝合金实测和预测成形极限曲线。从图5可以可看出，修改后的预测曲线考虑到了应变路径非线性次应变偏移的问题，明显优于原来的预测模型，最低点位置非常接近实测结果，相较于原模型，与测试结果的相关性更高，更能反映材料的真实性能。

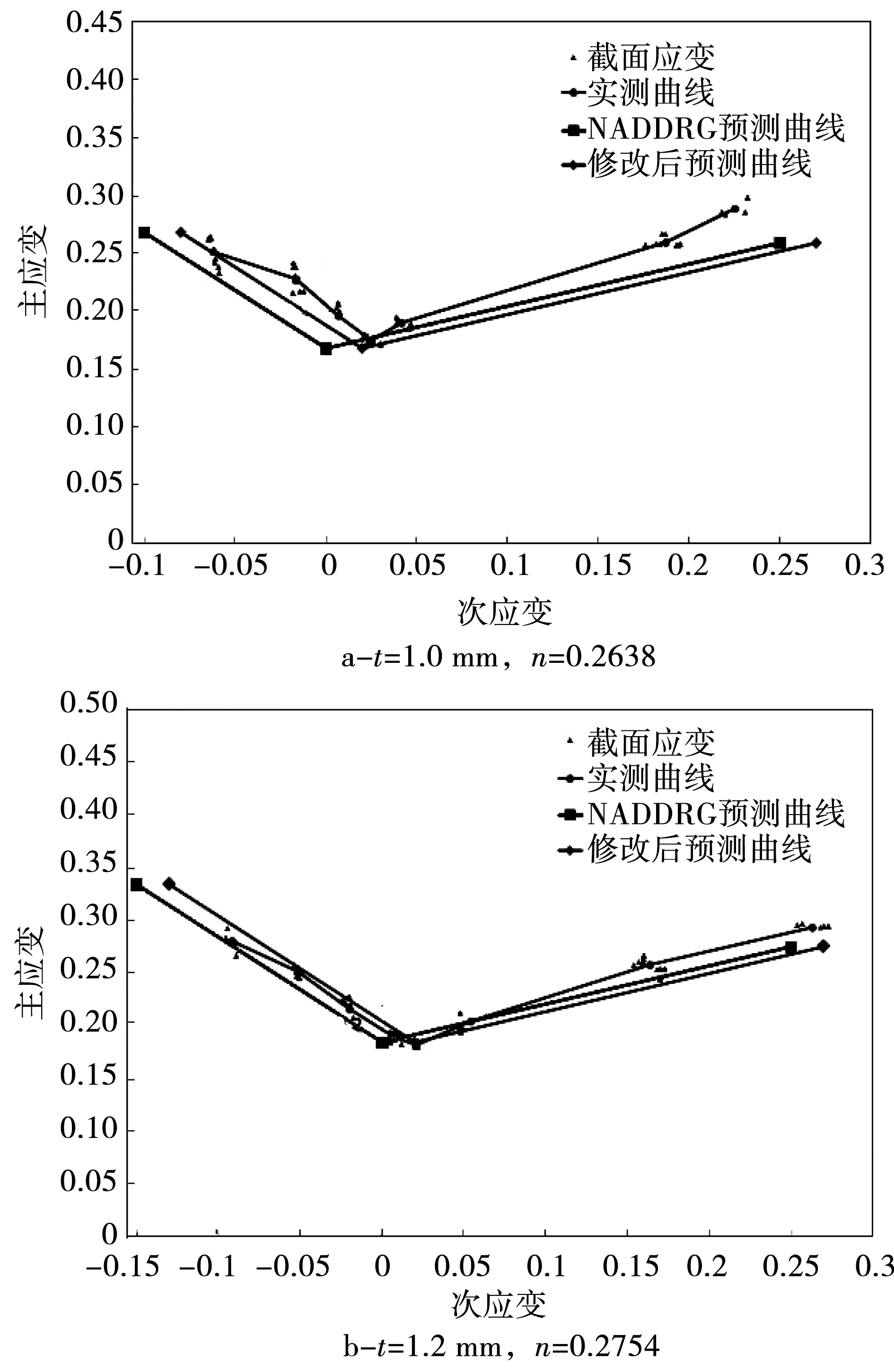
图5 不同厚度6016铝合金板实测和预测成形极限曲线

4 结 论

1)采用NADDRG模型预测6016铝合金板材成形极限曲线结果比较接近实际测试，但实际测试得到的曲线最低点次应变明显向右偏移，其主应变与预测结果基本一致。

2)通过分析得到曲线最低点的应变路径，可知其应变路径明显分为两个阶段：第一阶段的双向等拉伸应变状态导致主次应变同步增大，应变路径向右发展；第二阶段次应变基本保持不变直至试样发生失效，测试曲线最低点并不是平面应变点。

3)笔者对NADDRG模型进行修改，并采用不同厚度的6016铝合金板进行验证，修改后的预测模型曲线考虑到了应变路径非线性次应变偏移的问题，进一步提高了预测的准确性，与Nakajima法实测得到的结果更加吻合，预测结果更加可靠。