基于分位数回归的马尾松青冈栎混交林树高-胸径模型

孙拥康，汤景明，王 怡

（湖北省林业科学研究院，湖北 武汉 430075）

构建树高与胸径预测模型，是林业生产实践中快速、准确估测林木树高的常用方法，也是有效评估林分生长与收获的重要参考依据[1-2]。目前，已有许多专家学者对树高-胸径模型进行了深入研究，整体来看，已构建的树高-胸径模型形式以非线性模型和混合效应模型为主[3]。非线性模型通常采用最小二乘法（OLS）来进行参数估计，然而最小二乘法是基于均值回归，只能得到树高的平均预测，在处理具有尺度性的数据时往往会产生较大误差；此外，该方法要求模型误差服从独立正态分布假设，但在林业实际工作中，树高-胸径观测数据及模型的参数联合分布均很难满足该要求[4-6]。混合效应模型同时考虑固定效应参数和随机效应参数，既可体现样本总体的平均变化趋势，又可反映样本个体间的差异，相较于传统非线性模型拥有更好的灵活性[7]，但混合效应模型个体预测需要进行二次抽样来校正随机参数，对于大尺度区域的二次抽样不仅会大大增加调查成本，也会增大树高测量的误差[8]。加之，混合效应模型对数据信息要求较高，其应用数据条件必须是分组数据或纵向数据，如果数据没有这样的信息则无法使用该方法来进行分析，这就在某些情况下限制了模型的应用[9]。

分位数回归（Quantile regression）是Roger Koenker 和Gilbert Bassett 于1978年提出的一种回归方法[10]，其较经典的最小二乘法具有独特的优势在于[11-12]：1）分位数回归能够更加全面的描述被解释变量条件分布的全貌，而不是仅仅分析被解释变量的条件期望；2）分位数回归不受数据中异常点影响，估计结果对离群值表现的更加稳健；3）分位数回归对误差项并不要求很强的假设条件。近年来，分位数回归在林业研究中的应用越来越受到国内专家学者的关注。高慧淋等[13]利用分位数回归方法研究并拟合出了长白落叶松人工林最大密度线模型。马岩岩等[12]基于分位数回归方法构建了落叶松树干削度方程，比较分析了不同分位数及组合分位数的拟合与检验结果。辛士冬等[14]利用分位数回归模拟了人工樟子松树干干形，对比分析了不同分位数回归模型与传统非线性回归削度方程的预测精度。尽管也有部分学者应用分位数回归方法对树高-胸径模型进行了研究，如：王君杰等[15]基于分位数回归和哑变量方法构建了大兴安岭落叶松树高-胸径模型，得到了较好的模型预测效果。但从现有研究来看，一方面应用分位数回归方法开展林业树高-胸径生长关系的研究整体还较少；另一方面已开展的相关研究主要以纯林为研究对象，而以多树种、多层次的混交林为研究对象开展的研究还较少涉及[16-17]。基于此，本研究以湖北省林科院九峰试验林场马尾松青冈栎混交林为研究对象，在基础模型优选基础上，通过引入哑变量和分位数回归方法，构建混交林不同树种的树高-胸径分位数回归模型，以期为精确描述研究区混交林树高-胸径关系，进而促进森林质量精准提升和可持续经营等提供科学依据。

1 研究区概况

湖北省林科院九峰试验林场位于武汉市东郊（114°28′52″～114°31′53″E，30°30′1″～30°30′59″N），距市中心城区约20 km，总面积约333.33 hm2。海拔50～240 m；属亚热带湿润季风气候区，冬夏季季风交替明显；雨量充沛，年均降水量约1 200～1 400 mm，无霜期235 d；年日照时数为1 600 h，年均温度16.7℃；土壤以红壤为主，母岩多为石英砂岩、砂页岩，土层平均厚度为80 cm。优越的自然地理条件，适宜多种森林植物生长。场内主要乔木树种有马尾松Pinus massoniana、青冈栎Cyclobalanopsis glauca、湿地松Pinus elliottii、枫香Liquidambar formosana、麻栎Quercus acutissima、樟树Cinnamomum camphora、水杉Metasequoia glyptostroboides等；主要灌木树种有枸骨Ilex cornuta、山胡椒Lindera glauca、油茶Camellia oleifera、牡荆Vitex negundovar.cannabifolia、金樱子Rosa laevigata、野蔷薇Rosa multiflora等[18]。

2 材料与方法

2.1 数据来源

本研究数据来源于2019年对湖北省林科院九峰试验林场马尾松青冈栎混交林设置的3 块固定标准地和12 块临时标准地，标准地面积均为20 m×20 m，对标准地内胸径≥5 cm 的立木进行每木检尺，并对每块标准地各测树因子（胸径、树高、优势高、冠幅、株数等）和立地因子（海拔、坡度、坡向、坡位、土层厚度等）进行调查，共调查立木1 276 株（马尾松551 株、青冈栎725 株），林分年龄分布为18～35 a。将标准地调查数据按照3∶1 比例分为建模数据（9 块标准地，立木共计957 株，其中，马尾松426 株，青冈栎531 株）和检验数据（3 块标准地，立木共计319 株，其中，马尾松125 株，青冈栎194 株），模型数据见表1。

表1 模型数据统计Table 1 Statistics of model data

2.2 基础模型

用来描述树高-胸径关系的非线性模型有很多，本研究在参考国内外相关文献资料并结合混交林树高-胸径散点图变化趋势基础上，选取Richard 模型、Weibull 模型、Logistic 模型、Hossfeld 模型、Korf 模型、Gompertz 模型[19-20]6个代表性树高曲线模型作为候选基础模型，模型表达式见表2。

表2 5 个候选基础模型†Table 2 Five candidate basic models

2.3 哑变量的引入

构建包含哑变量的树高-胸径预测模型，不仅可实现模型对不同树种的相容性，也可在一定程度上既减少工作量又提高模型预测精度。本研究在候选基础模型优选基础上，引入含树种类型的哑变量，具体过程是将第i个树种定为Ki，将定性数据Ki转化为（0，1）[21]。即：

式（1）中：i=1、2，K1、K2分别为马尾松和青冈栎。

2.4 分位数回归

分位数回归最大的优势在于可以预测任意分位点处因变量的变化趋势，且不需要对模型误差要求严格的假设条件，因此，本研究选取了9 个分位点(τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9)构建不同树种的树高-胸径预测模型，利用加权最小一乘法统计各分位点的参数估计值，具体公式[22]如下：

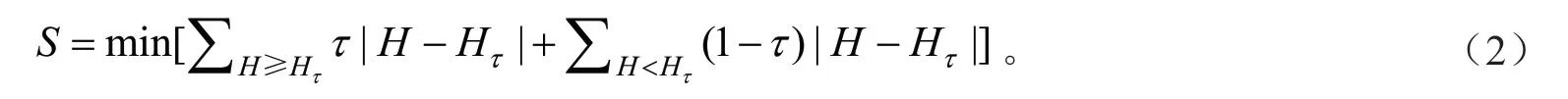
式（2）中：S为不同分位点估计值；H、Hτ分别为不同分位点τ的树高值与树高预测值；τ为分位点。

2.5 模型检验与数据统计

选用平均绝对误差（MAE）、均方根误差（RMSE）、确定系数（R2）3 个常用指标和T 检验对模型拟合精度及适用性进行检验与评价；图表、数据统计及回归分析分别基于Excel 2007、SPSS 17.0、Eviews 8.0 软件完成。

3 结果与分析

3.1 基础模型拟合与评价

利用马尾松、青冈栎全林调查数据对不同形式候选基础模型进行拟合与筛选，各模型参数估计值及评价指标值见表3。可以看出，6 个基础模型拟合确定系数R2均在0.71 以上，平均绝对误差MAE 介于0.96～0.97 之间，均方根误差RMSE介于1.18～1.20 之间，整体各模型精度较高且拟合结果无显著差异。根据模型精度较高且误差最小原则，并结合各模型参数生物学意义和模型收敛特性，本研究确定以模型Ⅰ（Richard 模型）作为马尾松青冈栎混交林最优树高曲线模型。

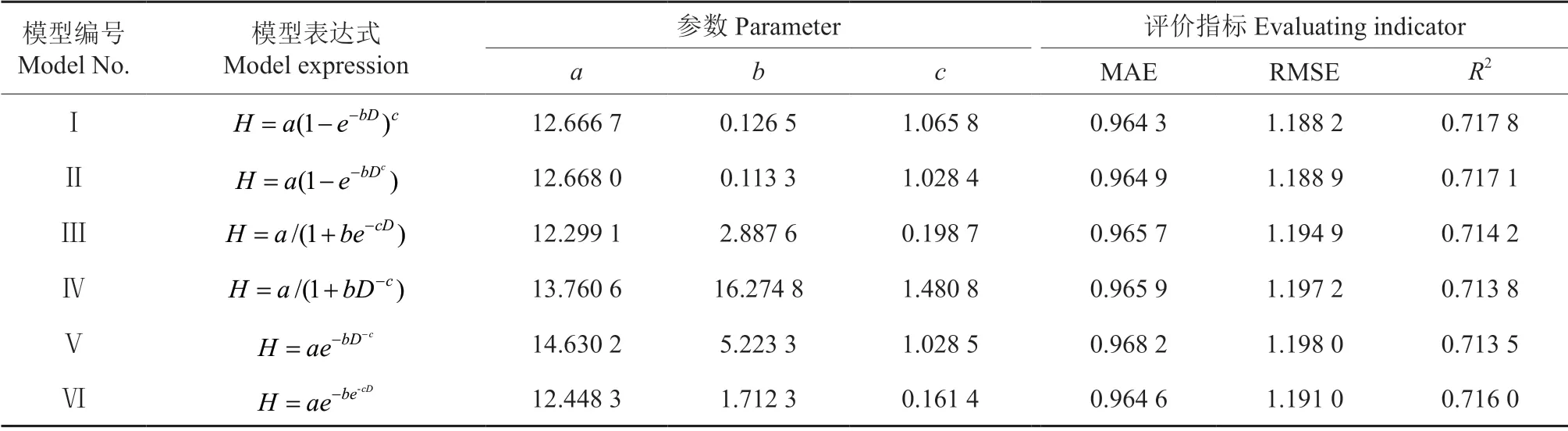
表3 基础模型参数估计及统计检验Table 3 Parameter estimation and statistical test of basic model

3.2 哑变量及分位数回归模型拟合与评价

在Richard 模型基础上，通过引入树种哑变量方法构建了含哑变量的马尾松青冈栎混交林树高-胸径模型：

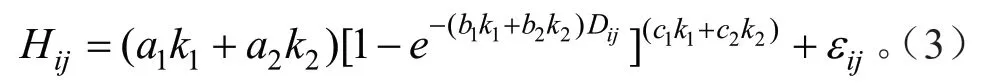
式(3)中：Ki为哑变量，当K1=1、K2=0 时为马尾松，当K1=0、K2=1 时为青冈栎；εij为误差项。

并对不同树种不同分位点(τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9)树高-胸径分位数模型进行了拟合与评价（表4），可以看出，基于树种哑变量的马尾松和青冈栎模型参数各不相同，也不同于基础模型求出的参数。从评价指标看，哑变量模型平均绝对误差MAE 介于0.87～0.92之间，均方根误差RMSE 介于1.0～1.2 之间，均低于基础模型；确定系数R2介于0.75～0.78，均高于基础模型，表明哑变量模型拟合精度整体要优于基础模型。而基于不同分位数模型的参数估计也各不相同，但各分位数模型评价指标表现出了一定的规律性，即平均绝对误差MAE 和均方根误差RMSE 随分位点的增加呈先减后增趋势，而确定系数R2则正好相反，呈先增后减趋势，除个别分位点处模型确定系数较低外，整体分位数回归模型确定系数均较高，介于0.77～0.91 之间，表明分位数回归模型整体预测能力要优于哑变量模型和基础模型。

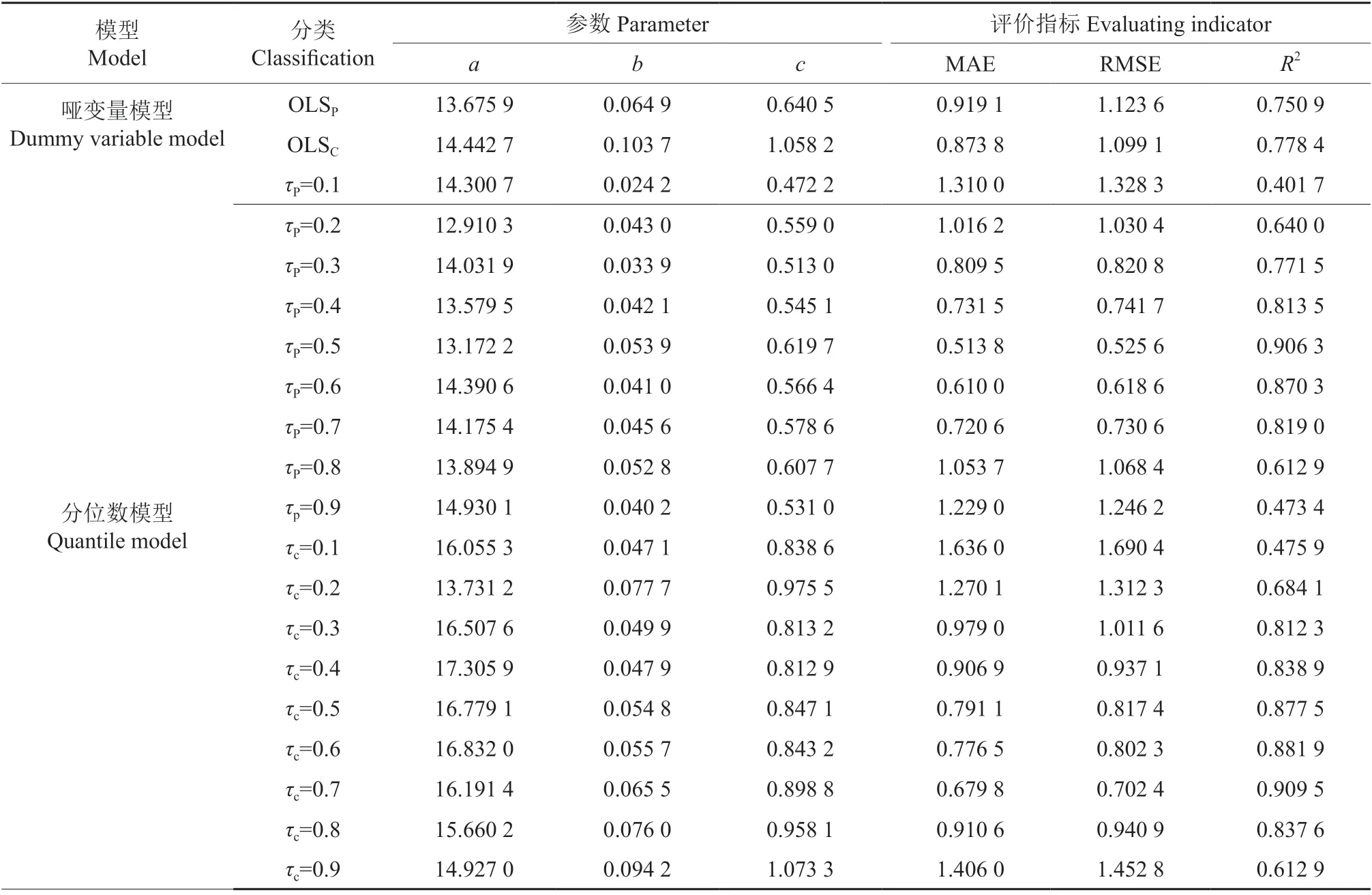
表4 哑变量及分位数回归模型参数估计及统计检验†Table 4 Parameter estimation and statistical test of dummy variable model and quantile regression model

为更直观分析分位数模型模拟树高曲线的变化趋势，分别对马尾松和青冈栎不同分位点的树高-胸径关系进行了拟合（图1），可以看出，通过分级拟合的树高曲线反映了相同立地条件下不同树种的生长情况。马尾松树高曲线整体较平缓，而青冈栎树高曲线则呈上升趋势，马尾松和青冈栎最优分位数模型分别为τ=0.5 和τ=0.7，说明同等立地条件下，青冈栎的生长势要高于马尾松，马尾松树高曲线更接近于总体平均水平。虽然不同树种在不同分位点的参数估计各不相同，但不同树种在不同分位点树高与胸径关系预测趋势走向基本一致，且各分位数曲线都穿过树高观测值，表明无论数据密集还是稀疏，含哑变量的分位数回归方法均能清楚描述树高曲线的变化规律，并达到良好的预测效果。

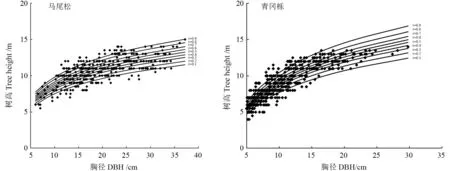
图1 不同分位数马尾松、青冈栎树高-胸径曲线模拟Fig.1 Simulation of height-diameter curve of Pinus massoniana and Cyclobalanopsis glauca with different quantiles

3.3 模型检验与综合评价

为更好地检验各树高-胸径模型预测水平，利用检验数据分别对基础模型、哑变量模型及分位数回归模型（选择最优分位数模型参与检验）进行了拟合，并对各树高-胸径模型预测值进行了配对T 检验，各模型独立检验及与综合评价结果见表5。从模型拟合情况看，各模型均具有较高的预测的精度，确定系数介于0.72～0.89 之间，由高到低排序为：分位数回归模型＞哑变量模型＞基础模型，与上述建模数据研究结果较一致；从配对T 检验情况看，不同树种模型预测结果整体差异性不大。但综合来看，分位数回归模型在描述树高曲线分布范围、变化规律以及模拟的稳健性上要优于哑变量模型和基础模型。

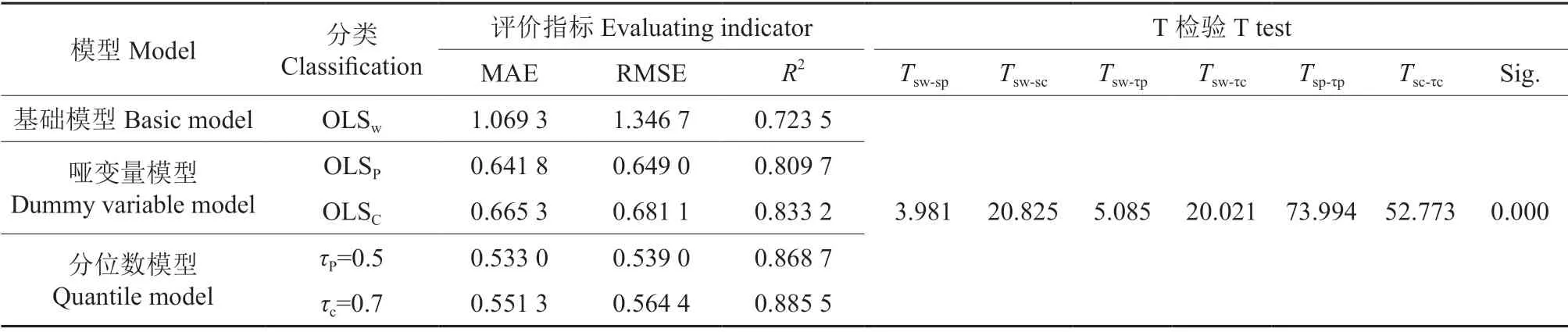
表5 不同树高-胸径模型的独立性检验†Table 5 Independence test of different tree height-diameter models

4 结论与讨论

4.1 讨 论

建立准确有效的树高-胸径模型在林业生产和实践中具有重要的现实意义。混交林是森林可持续经营的重要营林体制，因其林分树木个体差异和生境条件等的多变，树高-胸径关系往往是非线性的[24]。本研究利用6 个非线性树高-胸径模型对马尾松青冈栎混交林进行了模拟，结果表明综合表现最好的为Richard 模型，这与李海奎等[20]、张鹏等[25]研究得出树高-胸径最优模型为Weibull模型不同，这表明不同区域不同树种的树高-胸径拟合结果存在差异，树木种间竞争和生长、对环境的适应途径以及环境中的资源状况等均会造成混交林树高-胸径关系的多样[26]。基于哑变量和分位数回归方法构建的树高-胸径关系模型精度均高于传统回归方法，这与Bohora 等[27]、赵梦草等[28]利用分位数回归方法研究直径生长、树高生长的结论相一致，表明在对复杂的混交林进行研究时，将树种分组进行模型拟合是一个提高预测能力的可行思路，同时，也表明选取适当的非线性分位数回归方法相较于传统回归方法更能全面解释和获得树木生长信息，该方法可以应用到混交林或天然林的树高-胸径关系等的研究上，进而对其林分调查估测与科学经营提供科学指导。鉴于混交林林分结构和生长动态的复杂性和多变性，只考虑某些特定变量如树种、年龄等对树高胸径相关关系的影响，而忽略了环境效应、混交格局、种间竞争等的影响，难免会导致建立的模型适用范围受限、通用性不强等问题，因此，综合考虑多因素耦合的混交林树高-胸径模型势必成为未来研究的一个重要方向[23]。

4.2 结 论

本研究以湖北省林科院九峰试验林场马尾松青冈栎混交林为对象，通过对6 个代表性非线性树高-胸径基础模型优选，确定出Richard 模型为最优基础模型，在此基础上，通过引人树种哑变量和9 个分位点，构建了含哑变量的不同树种不同分位点的树高-胸径非线性分位数回归模型，结果表明：不同树种都有其对应的最优分位数模型，马尾松和青冈栎最优分位数模型分别为τ=0.5 和τ=0.7；整体看分位数回归模型拟合结果和预测能力要优于哑变量模型和基础模型；将分位数回归模型应用到混交林或天然林树高-胸径关系等的研究中是一个可行思路。鉴于本研究数据样本数量有限，只比较了树高-胸径模型的平均预测，而这种平均预测并不能代表整体数据结构的最佳关联性，如何既能考虑不同条件分布参数估计的差异，又能考虑整体数据内部之间的关联性还有待进一步研究[22,29]。