缺失数据下Topp-Leone分布的参数估计

郝淑颖

(荆楚理工学院 生物工程学院，湖北 荆门 448000)

0 引言

在利用试验数据进行统计推断时，经常会遇到数据的缺失，如进行寿命试验时有一些高可靠性产品的存在，要获得全部失效数据必然要经历很长的试验时间.为了节省试验费用,通常采用截尾试验来获得缺失数据样本，因此基于缺失数据的统计推断是一个重要且有意义的问题，如在文献[1-6]中罗倩，赵志文等讨论了在部分缺失数据样本下两个总体分布的参数估计和假设检验问题.Topp-Leone分布是一种具有有界支撑的连续单峰分布，可用于刻画元器件的寿命现象.目前已经有很多统计学研究者研究了这个分布的统计推断问题，并产生了一些研究成果.在文献[7]中GHITANY等研究了该分布的一些统计性质.文献[8-9]中MIRMOSTAFAEE等基于记录值讨论了Topp-Leone分布的Bayes统计推断问题.文献[10-11]中GEN等给出了Topp-Leone次序统计量的递推关系.文献[12-14]中FEROZE等在完全样本或者截尾样本下研究了Topp-Leone分布形状参数的极大似然估计和Bayes估计.

本文将进一步讨论在数据缺失样本下Topp-Leone 分布的参数估计问题，计算出参数的极大似然估计，并在不同的损失函数下得到了参数的Bayes和E-Bayes估计，且对各种估计进行分析.

1 极大似然估计及其渐近性质

设样本观测值服从Topp-Leone分布，其概率密度函数为

f(x,θ)=2θ(1-x)(2x-x2)θ-1,00.

(1)

假设对上述Topp-Leone分布进行n次独立观测，每次以概率P观测到样本值，以概率1-P丢失样本值.用(Xi,δi),i=1,2,…，n表示来自Topp-Leone分布总体的观测值，其中Xi表示来自Topp-Leone分布总体的第i个样本观测值，并且第i个样本观测值丢失，记δi=0，否则记δi=1.

下面求未知参数θ的极大似然估计.基于样本观测值(Xi,δi),i=1,2,…，n，则似然函数为

(2)

(3)

由极大似然估计的性质可得到如下定理.

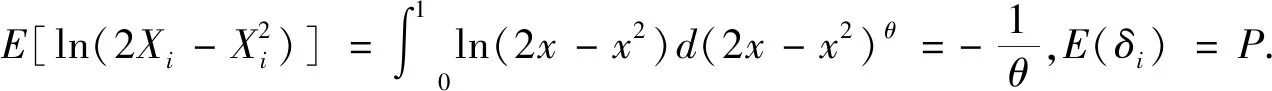
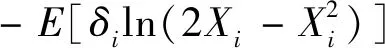
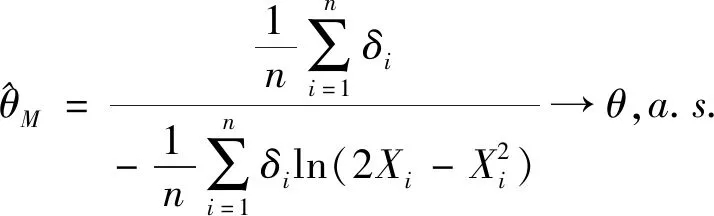
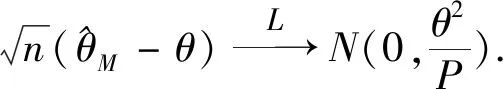
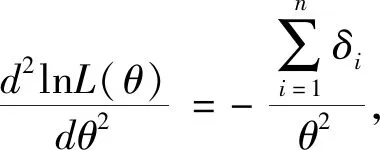
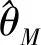
2 参数的区间估计与假设检验

在前面我们讨论了参数的点估计，有时要估计参数在某一范围中取值的情况，这样就是参数的区间估计.由第1部分的结论可以得到如下定理.

定理3 如果θ的极大似然估计由式(3)给出，则θ的置信度1-α的近似置信区间为

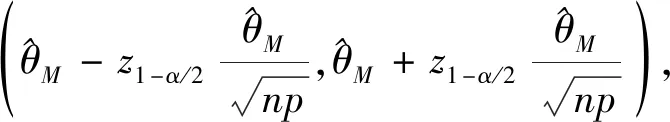
因此

于是θ的置信度1-α的近似置信区间为

下面讨论参数的假设检验问题.

H0:θ=θ0↔H1:θ≠θ0.

1) 对于假设检验

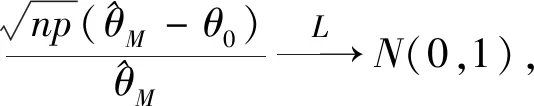
2) 对于假设检验H0:θ>θ0↔H1:θ≤θ0.

给定显著性水平α(0<α<1)，则检验的拒绝域为

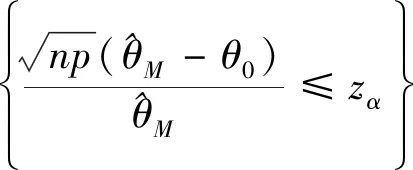
3) 对于假设检验H0:θ<θ0↔H1:θ≥θ0.

3 参数的Bayes及E-Bayes估计

在贝叶斯统计推断中“先验分布”和“损失函数”是参数估计精度的两个重要方面，最常用的是平方损失函数，由文献[15] 有下面的引理1.

引理1[15]设x=(x1,x2,…，xn)是来自某总体密度函数f(θ,x)的样本观测值，θ为其未知参数，则有

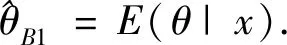
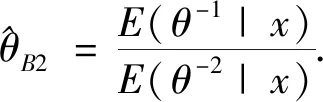
是未知参数θ的E-Bayes估计(expected Bayesian estimation)，其中π(a,b)是超参数a,b在集合D上的联合密度函数.

(4)

若取θ的先验分布为伽玛分布，其概率密度函数为

(5)

这里超参数a>0,b>0.

由式(4)、(5)，并根据Bayes公式可得到θ的后验密度为

(6)

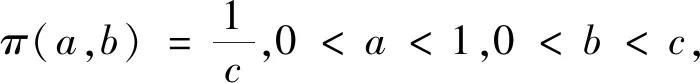
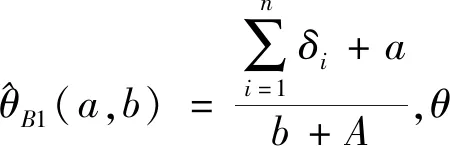
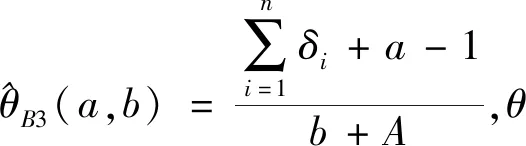
证明1)在平方损失函数下θ的Bayes估计为

根据定义1 ，则θ的E-Bayes估计为

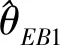
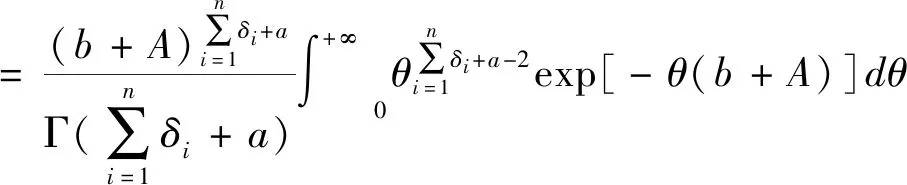
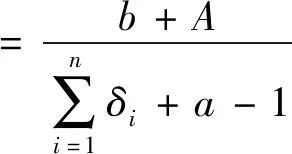
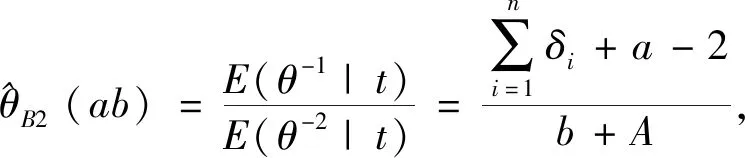
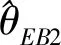
3) 由2)的证明可得θ的Bayes估计为

θ的E-Bayes估计为

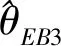
4 随机模拟

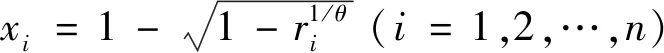
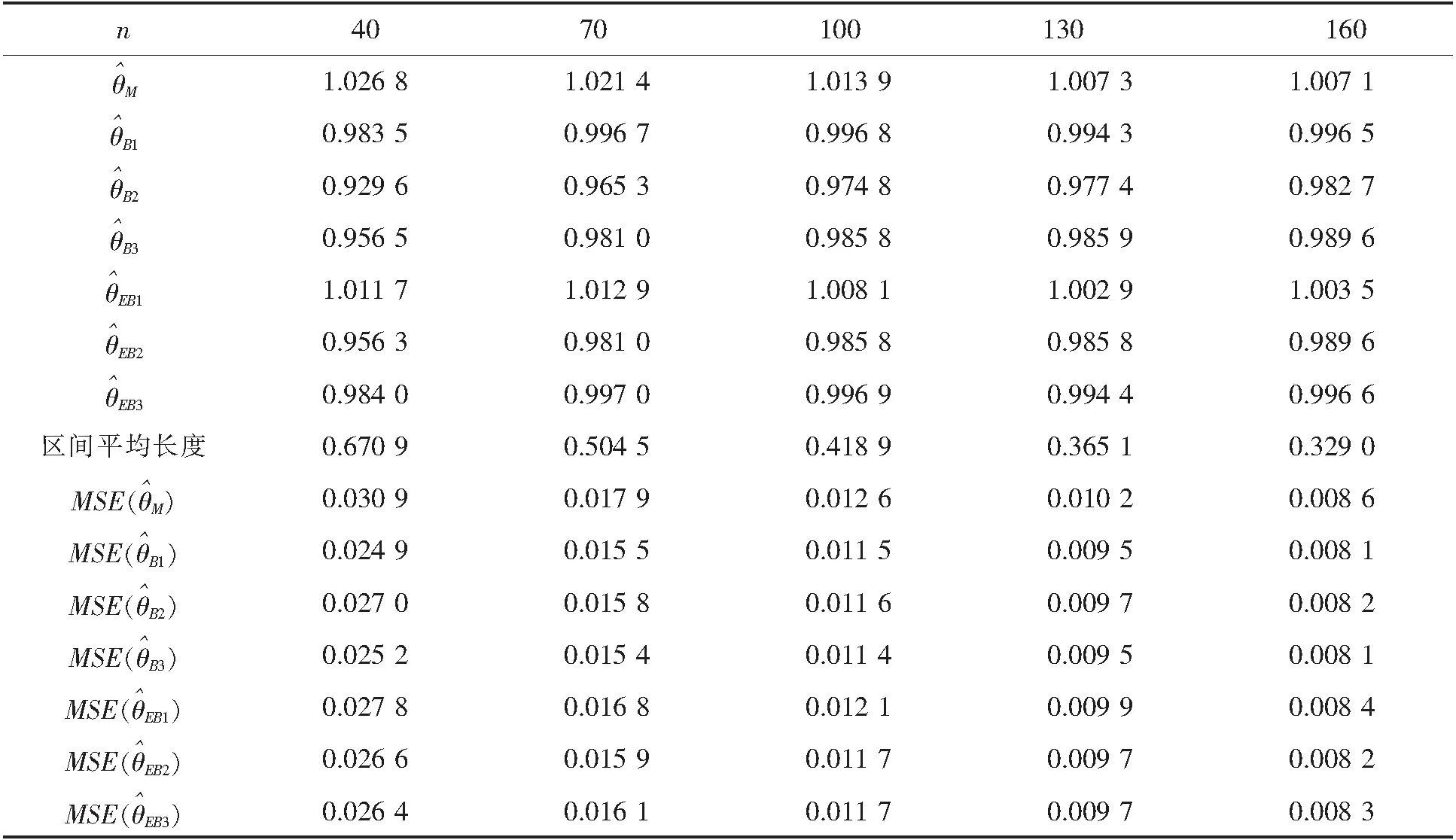
表1 参数估计的均值、均方误差及置信区间的平均长度

可以看到，参数θ的各种估计的均值都很接近真值.随着样本量n的增加，估计值之间越来越接近，置信区间的平均长度和均方误差都逐渐变小.参数的Bayes估计和E-Bayes估计的均方误差都要小于极大似然估计的均方误差，且在样本量较小时它们之间的差距更加明显.