基于三区间法的无人机发动机支架随机振动疲劳分析
王宣博,王子龙,王君凤,胡勇,韩世东
(航天时代飞鸿技术有限公司,北京 100094)
0 引言
活塞式航空发动机在中小型无人机应用广泛,该类型发动机一般通过调节风门和螺旋桨转速来改变发动机推力和无人机飞行速度,风门和螺旋桨转速变化,发动机振动频率也随之变化。活塞式航空发动机工作时产生的振动是无人机的主要振动来源之一,发动机产生的振动通过发动机支架传递到无人机机体,引起机体振动及噪声,导致部分结构及机载设备损坏,影响飞行安全[1]。振动疲劳是该类型无人机结构的典型疲劳问题,分析振动疲劳工况对增强飞机可靠性和寿命具有重要意义。
本文主要针对无人机的发动机支架结构进行研究,基于三区间法进行随机振动分析并结合仿真结果对支架结构进行优化,并对比优化前后的损伤情况,证明分析优化方法的可行性。
1 建立分析模型
1.1 动力学建模
发动机支架为点对称结构,由发动机转接板、支柱、减震橡胶等组成,如图1所示。因其点对称的支撑结构,建模时将模型切割为1/4大小,去掉半径<6 mm的圆角和倒角,简化减震橡胶处结构。采用Hypermesh作前处理,发动机用masses模拟,选取发动机质心位置进行加载,用MPC连接至发动机转接板孔位处,螺栓应力截面积取6 mm2。模型如图2所示。

图1 结构组成
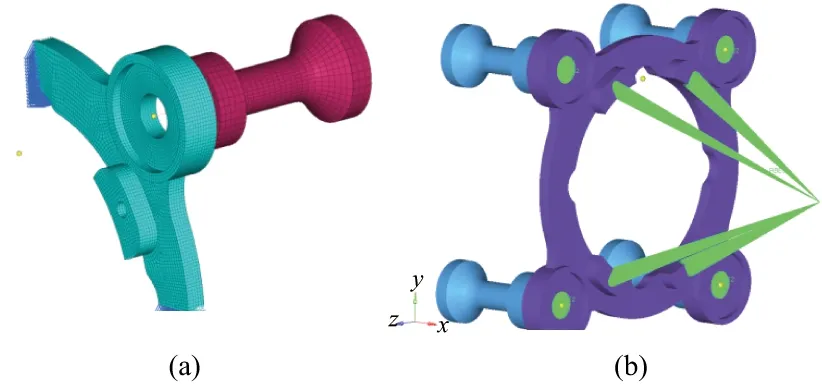
图2 简化模型
考虑到发动机转接板厚度的不均匀性,转接板采用solid单元,支柱采用solid单元,材料为铝合金,螺栓采用bar单元,材料为钢。各零件材料见表1,铝合金和钢的材料属性见表2。

表1 零件材料

表2 材料属性
1.2 边界条件
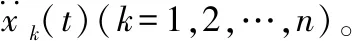
(1)
自相关函数代表随机振动过程加速度在时域内幅值的变化情况,其幅值呈正太分布,根据帕斯瓦定理,信号的平均功率在时域和频域守恒。对自相关函数作傅里叶变换,得到自功率谱密度函数如下:
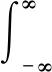
(2)
采用随机振动信号的加速度总均方根值评估随机振动工况的严酷度。运用功率谱密度计算方法求得加速度的总均方根值如下:
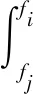
(3)
式中fi、fj分别为随机振动频率的上、下限。
振动测试频率为12.5 Hz,振动激励范围是15 Hz~500 Hz,振动分析选取1阶衰减对数频率范围f3=4×f0,得出数据绘制图3。
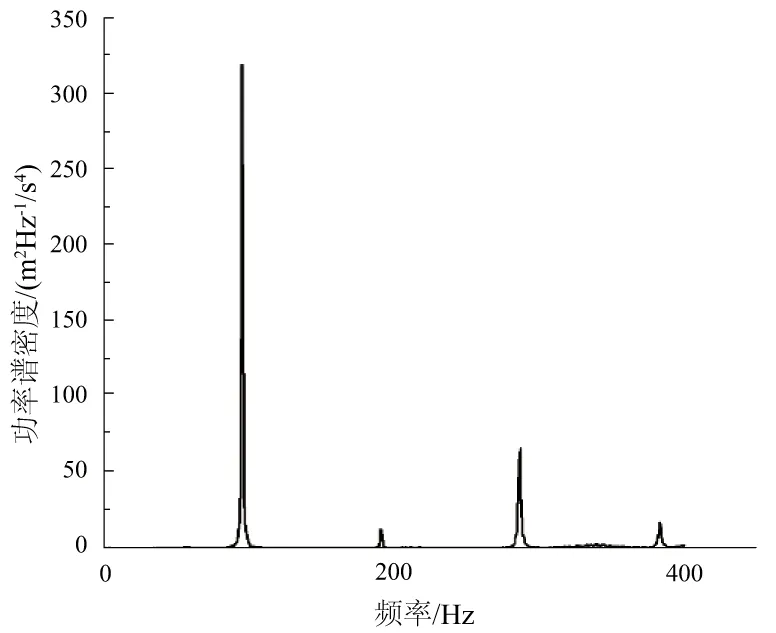
图3 随机振动曲线
2 仿真计算
2.1 固有频率分析
发动机支架疲劳是使用过程中长期处于振动环境产生的,疲劳分析是基于动力学仿真计算的基础。根据动力学仿真结果,结合材料的疲劳特性对疲劳寿命做出评估。因此,先进行固有频率计算,得到前6阶固有频率如表3、图4所示。
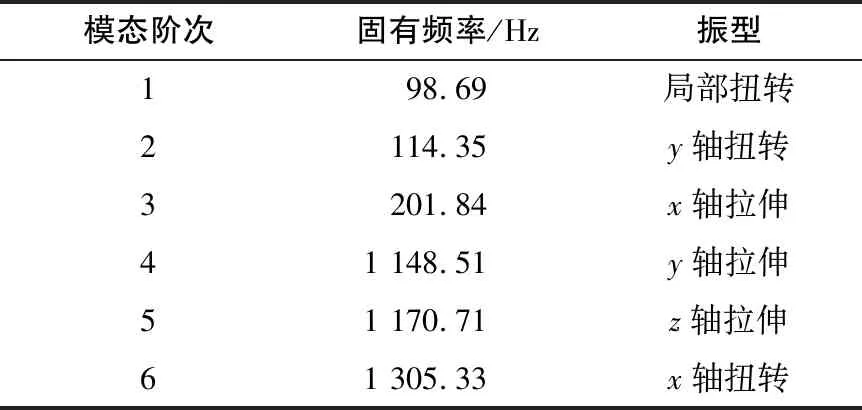
表3 固有频率统计
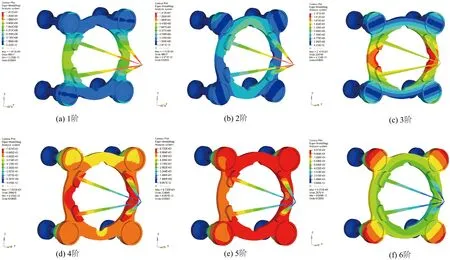
图4 固有频率分析
2.2 随机振动分析
建立工况,将振动频率曲线输入TABLED1,定义DTI,阻尼比0.02,结构激励方向沿全局坐标y向和z向。设置频率范围为0~600 Hz,特征值分析使用耦合质量矩阵法,得到发动机支架的位移和应力云图如图5所示。
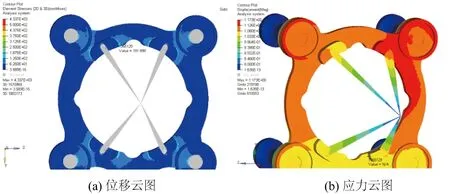
图5 随机振动下的发动机面板位移和应力云图
由图5可知,发动机在安装凸台过渡区的应力较为集中,大小为191.90 MPa。由图6可见,试验飞行过程中安装凸台过渡区的位置也出现了裂纹和断裂现象,证明仿真结果准确可信。

图6 发动机面板裂纹
图6圈内区域截面形状过于突变,容易产生应力集中,在安全方面具有隐患,对该区域进行优化,使区域内的集中应力分散并过渡至发动机支架面板内。对截面进行过渡处理,将该凸台位置与面板的连接处设计为带拔模角度的凸台,拔模角度为40°,并加厚了发动机支架面板厚度,如图7所示。
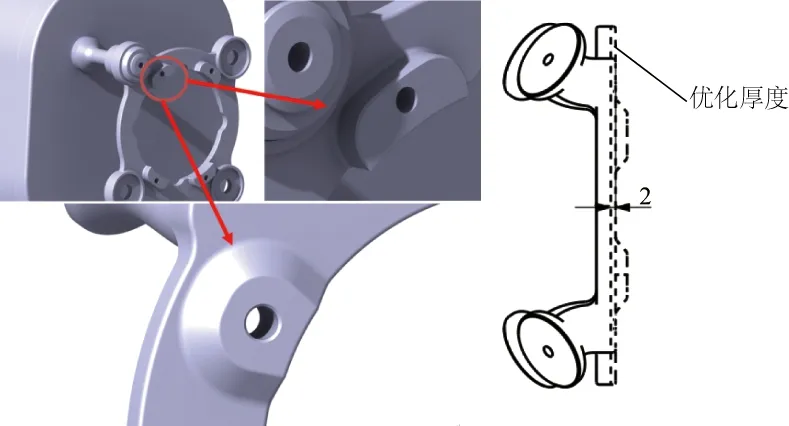
图7 优化凸台应力集中区域
重新对优化后的发动机面板进行随机振动分析,工况和边界条件同上,得到应力和位移云图如图8所示。由图8可见,优化后在发动机安装凸台处的应力减小为12.83 MPa。证明增加拔模角度对应力集中具有很大的改善。
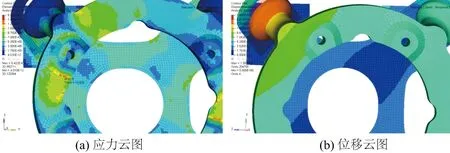
图8 优化后应力与位移云图
2.3 疲劳分析
根据Steinberg的三区间理论,结构在随机振动下的响应呈高斯分布,通过模态扩展和合并计算(表4),结合Mine线性累积损伤定律进行疲劳计算。

表4 高斯分布三区间法
(4)
(5)
(6)
(7)
根据随机振动仿真结果可知,优化后的发动机支架最大等效应力1σ为12.83 MPa,2σ为25.66 MPa,3σ为38.49 MPa。
由材料的ε-N曲线拟合公式可得
lgN=18.829 4-6.662 2lgσ
(8)
当D=1时,可得到寿命T:
(9)
得出T=44 831 167≈4.48×107,满足GJB150.16A[7]振动环境要求。
3 试验结果
将优化后的产品进行生产制造,对安装的后续机型进行了一系列的系统试验,未出现支架面板的裂纹问题,满足飞行器包线中各任务段的使用要求。优化后产品示意图如图9所示。

图9 优化后产品示意图
4 结语
本文针对某型无人机发动机支架建立动力学模型,并基于试验数据得到了随机振动的自相关函数,确定了振动疲劳边界条件,对结构进行模态仿真和振动疲劳分析,得出飞行过程中发动机支架安装凸台容易产生应力集中且发生振动疲劳损伤的结论。
针对此问题,提出了修改凸台连接处拔模角度的优化方案,使用三区间理论对优化后的凸台结构进行疲劳计算,优化后的疲劳寿命可达4.48×107,满足实际工程要求,证明了分析方法和优化方法的可靠性。
本文提出的方法可以不局限于文中论述的结构产品,还可应用于其他以活塞类航空发动机为动力的无人机所受振动影响的结构零部件的设计和校核工作。

