低频条件下二维振动应力释放规律研究

刘敏，杨扬，左敦稳

(1.南京航空航天大学 机电学院，江苏 南京 210016；2.中国电子科技集团公司 第二十八研究所，江苏 南京 210016)

0 引言

紧固件连接孔是飞机疲劳损坏的薄弱环节，因交变应力的作用，源于孔的疲劳裂纹极易扩展到受力结构件上而引发灾难性的事故[1]。开缝衬套冷挤压技术是目前国际上最先进的抗疲劳制造技术之一。它能在紧固孔附近形成一定厚度的残余压应力层，在增强紧固孔疲劳寿命的同时，还可有效提高其抗应力腐蚀和腐蚀疲劳的能力[2]。近20年来，研究者们对冷挤压孔工件的应力释放问题进行了一系列研究。ABDOLLAHI E等[3]结合非线性各向同性和非线性Chaboche运动硬化模型，模拟了铝合金2024-T3的循环塑性行为中的应力释放。MAXIMOV J T等[4]通过研究中碳钢冷挤压孔工件在循环拉伸应力下的应力释放过程，提出了应力释放的数学预测模型。但目前开缝衬套冷挤压技术所引入的应力在复杂交变应力工况下的释放规律尚不清楚，制约了这项技术的广泛应用。因此，关于开缝衬套冷挤压孔周边残余压应力的释放规律研究亟待开展。

振动时效具有清洁、高效、操作简便等显著优点，已逐渐取代其他方法成为残余应力释放的主要技术[5]。本文研究对象为小直径开缝衬套冷挤压孔工件，其共振频率较高，在15 kHz以上。而该孔工件在工况下受低频(100 Hz以下)振动载荷较多，因此传统的共振型二维振动[6]时效无法适用。为了便于模拟孔所受的复杂交变应力载荷，本文设计一种二维振动应力释放装置，使用频率在100 Hz以下，且频率连续可调，能输出多种振动轨迹图形，并基于此开展低频条件下二维振动法应力释放规律的研究。

1 二维振动法应力释放装置设计

1.1 低频二维振动实现原理

根据李萨如图形合成原理，频率比和相位差不同的两个正弦信号可以合成不同的轨迹图形。为了便于研究，本文设x方向的激励信号初相位是0，y方向的激励信号初相位是θ。根据二维振动合成理论，两个振动在x、y方向的合成振动轨迹为

(1)

其中：Ax、Ay分别为x、y方向的振动幅值；fx、fy分别为x、y方向的振动频率；θ分别为x、y方向激励信号的相位差；t为时间变量；x(t)为柔性铰链输出端沿x轴方向的位移；y(t)为柔性铰链输出端沿y轴方向的位移。

为实现两个垂直方向的纵振解耦、输出端振动参数即李萨如图形轨迹灵活可调，本文设计出一种双激励非共振型二维振动应力释放装置，其原理图如图1及图2所示。

图1 二维振动受力图

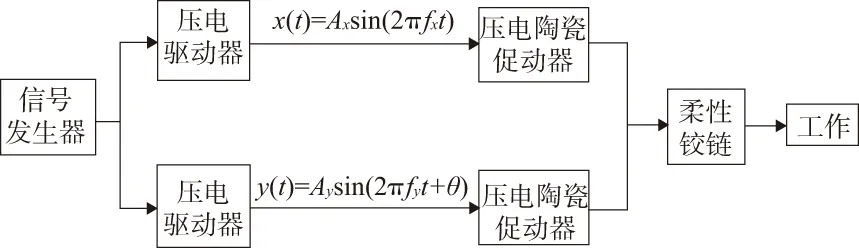
图2 二维振动系统原理图

二维振动系统激振机构的驱动单元选择压电陶瓷促动器，x、y方向分别由一支压电陶瓷促动器产生纵向振动，将位移载荷传递给柔性铰链的输入端，使输出端产生二维振动轨迹。

1.2 柔性铰链设计

柔性铰链是通过机构的自动变形进行力传递的，有着运动耦和及放大输出位移作用[7]，其中常用的直圆形柔性铰链受力示意图如图3所示。当铰链的一端处于固定状态时，对其另一端施加一定的力F和力矩M，使得柔性铰链产生θ角度角位移，此时铰链的柔度大小为[8]

图3 传统直圆形柔性铰链模型

(2)

从式(2)可以看出，铰链的柔度大小受多因素影响，主要有材料的弹性模量E、铰链沿z向的厚度b、切割半径r以及厚度t。为了使工作面在获得两个纵向振动的同时不受其他方向振动的扰动，需适当地控制t和r。

本文选用一种并联式直圆形柔性铰链(图4)，可以使相互垂直的两个纵向振动同时传递到工作面上，实现两个垂直方向的运动合成。

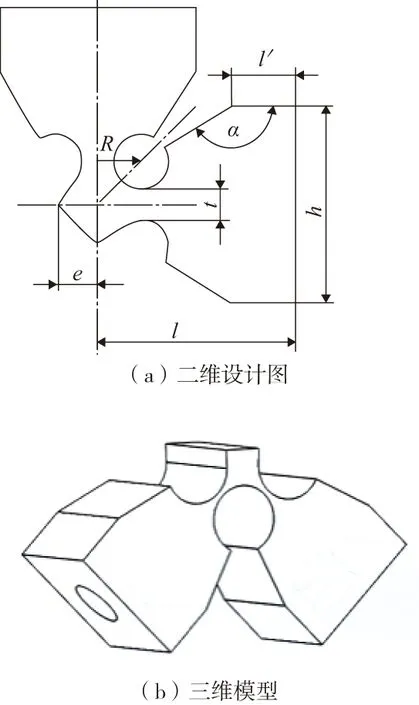
图4 柔性铰链结构示意图

1.3 谐响应分析及模态分析

本文通过对铰链输入端施加正弦位移载荷，激励频率范围10～100 Hz，计算输出端在指定振动频率下的位移响应，采用完全法(Full法)进行谐响应分析。考虑到柔性铰链应具有良好的拉伸刚度和旋转刚度，一般情况下选用弹簧钢或合金弹簧钢，本文选用30CrMnSi。30CrMnSi材料的密度ρ=7 850 kg/m3，弹性模量E=200 GPa，泊松比μ=0.3。结合谐响应分析结果，在参数为r=3.25 mm，t=0.5 mm的条件下，柔性铰链的输出性能较好，输出端的轨迹可以呈现较为理想的李萨如图形，符合本文设计要求。

对所设计的柔性铰链结构进行模态分析，发现其前4阶共振频率分别为1 057.1 Hz、5 478.5 Hz、6 512.4 Hz、8 824.2 Hz，均在100 Hz以上。在本装置中，实际工作频率在100 Hz以下，远远小于各阶共振频率，所以不会产生共振现象。

综合考虑柔性铰链的动态特性、模态特性，本文选取的一组柔性铰链的结构参数和材料参数如表1所示。

表1 柔性铰链几何参数表 单位：mm

2 二维振动系统振动特性测试

为了确保搭建的系统能够输出满足需要的振动轨迹，在仿真分析的基础上，对组装好的二维振动系统的振动特性进行检测，并与理论设计要求进行比较。采用PCB Piezotronics三轴加速度传感器进行在位动态测量，并将采集的加速度动态数据进行二次积分处理以获取对应的速度和位移数据，当振动输出端的位移轨迹符合李萨如图形规律的结果下可验证振动系统的可行性。主要测量步骤如下：

1)配置连接PCB传感器，通过磁吸底座将传感器固定在柔性铰链顶端运动输出面，传感器y方向朝上；

2)指定激励信号，调节两激励信号的频率比和相位差，频率比变化范围为1∶1，1∶5，1∶10，相位差变化范围为0，π/4，获得6条测试数据；

3)数据处理，使用MATLAB软件对测得的振动加速度数据进行分析处理，获得振动输出端位移数据并绘制位移轨迹图。

将测得的振动加速度信号经两次频域积分处理[9]计算后，获得6种图形参数下测得的位移图形如表2所示。

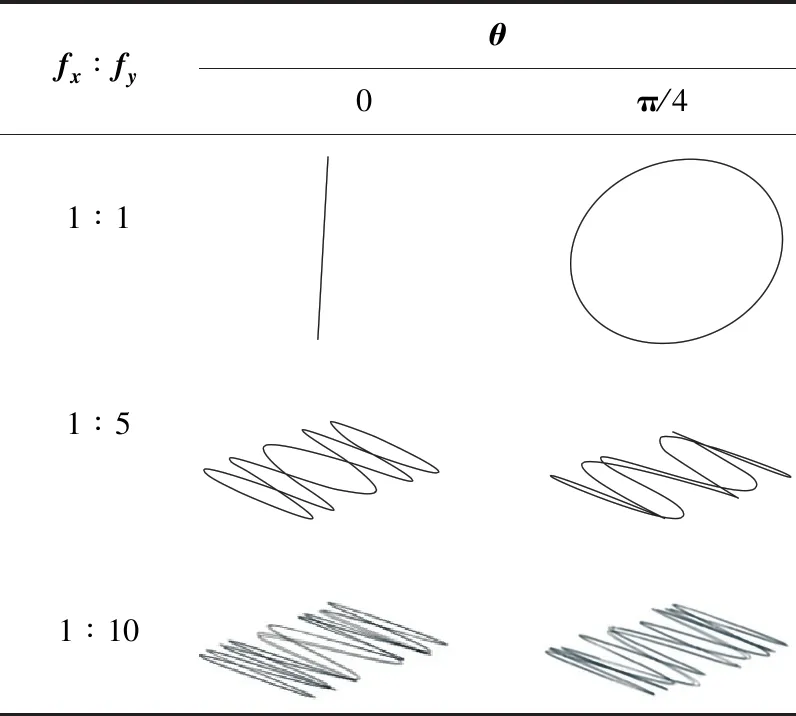
表2 振动加速度积分处理后的位移轨迹图

由表2可知，柔性铰链输出端在给定的激振频率比和相位差的条件下，能输出大致符合李萨如图形规律的位移运动轨迹。虽然测试所得的位移轨迹图形与理想图形存在偏差，但均在误差允许范围内，引起误差的原因可能与铰链的柔性、压电陶瓷促动器的位移输出精度等因素有关。

在验证了二维振动系统的柔性性能之后，需对其刚性性能进行验证。选取频率比为1∶1、相位差为0的最简图形对柔性铰链的运动刚度进行测试，激振频率为10 Hz。改变激励电压幅值，测得振动系统输出端的运动轨迹为沿y向的直线，位移轨迹峰值与激励电压的关系如图5所示。

图5 二维振动系统输出特性曲线

由输出特性曲线可知，二维振动系统输出位移幅值最大，可达320 μm，且位移幅值正比于电压幅值。因此可验证本文所设计加工的二维振动系统在刚度输出方面也满足设计要求。

3 低频二维振动应力释放实验

3.1 实验方案设计

实验所用工件材料为2A12铝合金板材，外径80 mm，中心孔直径11 mm，经开缝衬套冷挤压处理(图6)。

图6 冷挤压预处理工件图

实验所需正弦激励信号由信号发生器产生，经压电驱动器放大后输入至压电陶瓷促动器，同时用示波器显示信号波形质量。搭建二维振动法应力释放实验平台如图7所示。

图7 低频二维振动法应力释放实验平台

本实验中，影响二维振动法应力释放效果的关键因素有激振频率、相位差、振幅、激振时间、工件转速等。其中，两激励信号的频率比fx∶fy、相位差θ共同决定了振动输出端的轨迹图形，进而决定了单位时间内激振力的方向。本实验中选取基础频率为f=10 Hz，频率比fx∶fy和相位差θ的6种组合方式(表2)。激振电压V=10 V，激振时间为t=10 min，工件转速为n=5 r/min。按照上述实验条件，进行了6组实验。

3.2 实验结果分析

选取冷挤压过程中挤压芯棒挤出面进行研究，在孔周围到孔壁距离间隔1 mm取点，9 mm范围之外间隔2 mm取点。每个工件共取11个点，测量范围为距孔壁13 mm。测量同一点振动处理前后的径向应力SL和切向应力ST，振动前后应力对比图如图8所示。

分析图8可知，振动处理后工件周围应力呈现明显变化，且随着频率比的增大，应力变化幅度增大。分别对比不同方向的应力，切向应力的波动变化幅度明显大于径向应力。二维振动处理后，切向应力的变化可按到孔壁的距离分为两个区域：1～6 mm范围的测试点切向压应力减小，6～13 mm范围测试点切向压应力增大。

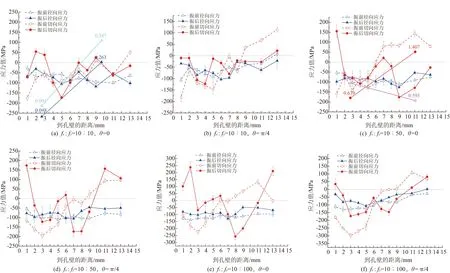
图8 振动前后应力对比图

因此将工件周围应力场划分为冷挤压已强化区域(距孔壁1～6 mm)、未强化区域(6～13 mm)，关注已强化区域内的径向应力和切向应力的变化并进行分析。

强化区域内振动前后平均应力变化率结果如图9所示。综合分析可知，随着频率比的增大，工件内部应力变化率总体呈现增大趋势，且在相同频率比下，相位差θ越大，应力变化率越大。

图9 强化区域振动前后平均应力变化图

4 结语

1)本文设计了一种低频非共振型二维振动应力释放装置，实现了在100 Hz以下频率连续可调输出稳定的振动轨迹。

2)基于有限元分析方法对所设计的二维振动系统进行模态分析和谐响应分析；使用PCB三轴加速度传感器对二维振动系统振动特性进行测试，验证了所设计二维振动应力释放装置的有效性。

3)对二维振动处理前后的工件进行应力测量，可知相位差与频率比综合作用于二维振动应力释放规律，相位差越大，应力变化率越大，同时，频率比的增大，也使应力变化率明显提高。