驱动方式与轮径差对悬挂式单轨车轮磨耗的影响分析

高润稼，曾京，戴鑫亮

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

悬挂式单轨作为一种新型的轨道交通系统具有较强的地形适应能力，其建设周期短，工程造价低，景观效果好[1]，近年来在全国多地得到了应用。与传统采用钢轮的轨道交通车辆不同，悬挂式单轨一般采用实心或充气橡胶轮胎。在列车运行时,橡胶轮胎可充分发挥其缓冲减振效果及较高黏着力的优势,可使车辆具有较高的加速、减速性能,但同时也不可避免地增大了车辆的运行阻力[2]。悬挂式单轨在运行过程中，走行轮的磨损往往是比较严重的，走行轮的过度磨损将影响车辆的启动、制动过程中的加减速性能，危及行车安全。

国内外许多学者都对单轨车辆轮胎磨损进行了研究，王国林等人提出采用虚拟外倾方法有效降低了走行轮胎磨损，并改善了其磨损均匀分布程度[3]；黄继刚等人提出了通过改变0°带束层弹性模量来控制走行轮轮胎偏磨的方法[4]；文孝霞等人探究了车辆中央悬挂参数刚度、走行轮定距对轮胎磨损的影响趋势[5]。

现阶段悬挂式单轨车辆走行轮的驱动方式主要有两种——独立驱动和同步驱动。为了选取合理的驱动方式以降低走行轮磨耗，本文将探究这两种驱动方式对走行轮磨耗的影响。

悬挂式单轨车辆走行轮在刚出现磨耗时，在不影响车辆正常运行时一般不会立即更换轮胎，此时走行轮之间会出现一定的轮径差。这种情况下车辆在后续运行过程中轮径差是会进一步加大还是减小，也是值得研究的问题。因此本文还将以磨耗功为依据，探究初始轮径差对走行轮后续磨耗的影响。

1 研究方法与计算模型

1.1 悬挂式单轨动力学模型

本文所研究的悬挂式单轨列车主要由车体、构架、悬吊装置、摇枕、走行轮、导向轮、稳定轮、一系橡胶堆、二系悬挂装置等组成。利用多体动力学计算软件UM建立单节编组的悬挂式单轨车辆系统多刚体动力学模型，如图1所示。

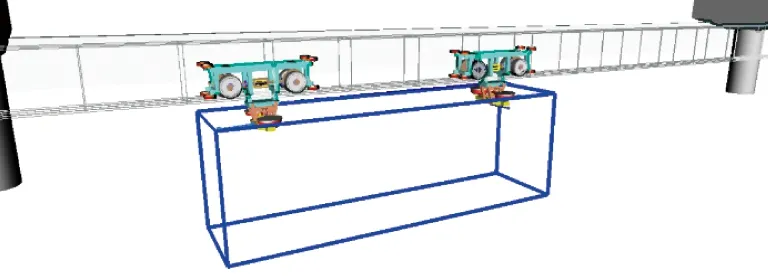
图1 悬挂式单轨动力学模型

车辆主要参数如表1所示。

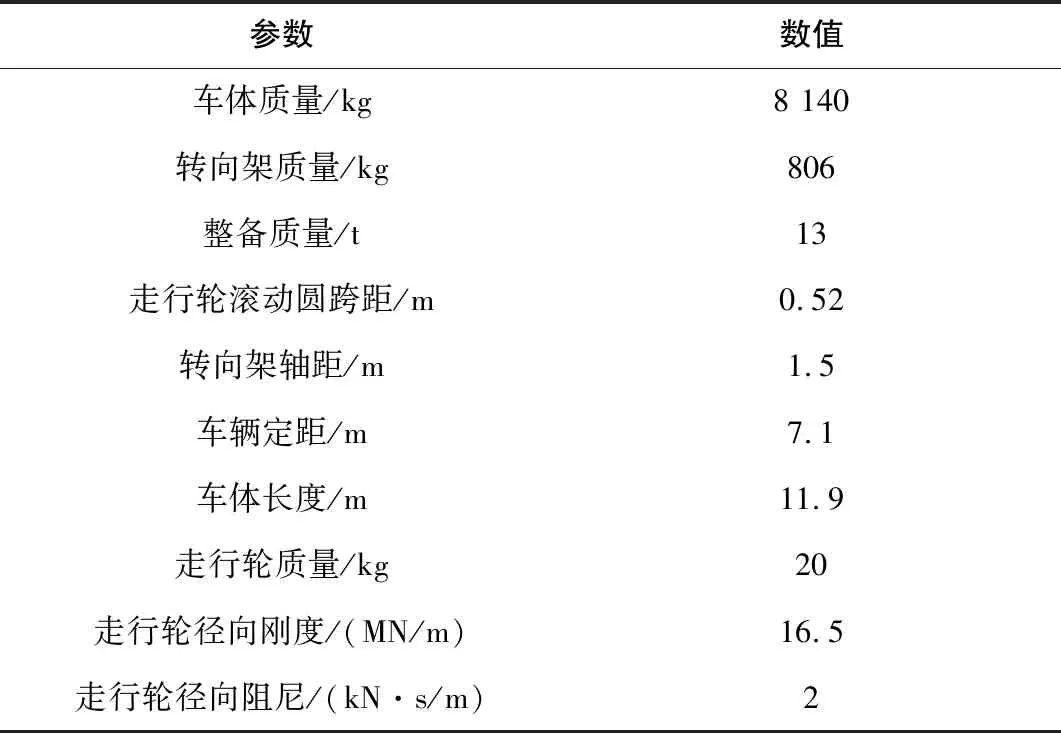
表1 车辆主要参数

考虑走行轮和导向轮在轨道梁内运行过程中侧倾角度较小，故采用基于弹性地基梁理论的Fiala轮胎模型来描述悬挂式单轨轮胎与轨道梁的相互作用关系。车辆模型中的减振器阻尼特性考虑为非线性，采用Maxwell模型来模拟抗横摆减振器、横向和垂向减振器的阻尼力。垂向止挡、横向止挡和部分悬挂元件亦为非线性。

由于不同的驱动方式可能对走行轮的磨耗程度有不同影响，因此建立独立驱动和同步驱动的车辆模型，其原理如图2所示。

图2 驱动方式原理图

独立驱动转向架采用4个驱动电机分别驱动每个走行轮，通过齿轮箱里的锥齿轮，可实现传动的换向。

同步驱动转向架的驱动电机位于构架的中部，差速器位于前后轮之间，驱动电机将动力传至前后差速器，差速器中的齿轮传动装置能够合理分配两侧车轮的转矩和转速，因此左、右两个走行轮可实现独立旋转。

1.2 走行轮磨耗模型

悬挂式单轨采用实心橡胶轮胎，车辆正常运行时，由于轨道梁的走行面存在不平顺的激扰，走行轮会出现纵向和横向滑移，走行轮受到轨面的摩擦力所做的功，从而加速轮胎的磨损。实际上橡胶轮胎的磨损是一个十分复杂的过程，包含了疲劳磨损、磨粒磨损、机械-化学腐蚀磨损等过程[6]。

由于直接计算橡胶轮胎的磨损量较为复杂，现在大都采用磨耗功理论定性地评价轮胎磨损的程度，磨耗功模型基本假设是单位体积的磨损量与磨耗功成正比[7]。磨耗功是轮胎与地面发生摩擦剪切、滑移的能量表现，与磨耗有很大的相关性[8]。磨损体积速率v与磨耗功率Wf的关系为

(1)

式中b0、b1为与花纹块磨损相关的材料参数。

本文以单位面积的磨耗功来衡量轮胎的磨耗性能，单位面积的磨耗功WA可表示为

WA=∬μdPdL

(2)

式中：μ为胎面与地面的摩擦因数；P为接触面上单位面积正压力；L为相对于接触面的滑移。

分别考虑每个轮胎的纵向磨耗功Wx和横向磨耗功Wy，则总磨耗功为

W=Wx+Wy

(3)

1)纵向磨耗功

走行轮的纵向磨耗功为轮胎的纵向滑移量×纵向摩擦力。产生纵向滑移时走行轮的滚动速度与走行轮的前进速度不相等，两者的差值即为相对滑移速度。因此纵向磨耗功可表示为

(4)

式中：ω为轮胎转动的角速度；r为轮胎滚动圆半径；v为轮胎前进速度；Fz为轮轨垂向力；μ为胎面与地面的摩擦因数；dt为测点时间间隔。

2)横向磨耗功

走行轮的横向磨耗功为轮胎的横向滑移量×横向摩擦力。由于轮胎的横向滑移量可以直接测得，因此横向磨耗功可表示为

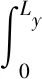
(5)

式中dy为轮胎横向位移。

1.3 磨耗功的仿真计算

仿真中直线工况车速设为60 km/h，曲线工况曲线半径为200 m，车速设为40 km/h；轨道梁的走行面施加实测不平顺激扰，仿真时长为20 s,采样时间间隔Δt为0.01 s。分别输出走行轮的垂向力Fz、走行轮角速度ω、走行轮前进速度v和走行轮横向滑移量dy。其中走行轮的垂向力Fz和走行轮横向滑移量dy时域上的结果如图3、图4所示(本刊为黑白印刷，如有疑问请咨询作者)。

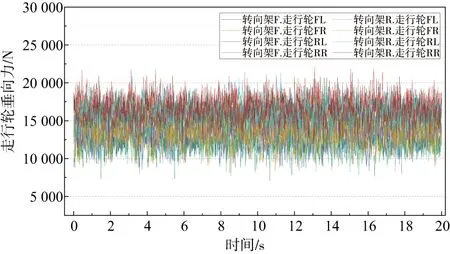
图3 走行轮垂向力

图4 走行轮横向滑移量

根据式(4)-式(5)补充基于数值仿真离散形式的磨耗计算公式：

(6)

(7)

式中：n为采样点序号；N为采样点总数；Δt为采样时间间隔；Δy为相邻采样点的轮胎横向位移。

将仿真得到的以上参数的数据结果，带入式(6)-式(7)可分别计算出每个走行轮在时域过程中的纵向磨耗功与横向磨耗功，再由式(3)即可算出单个走行轮总的磨耗功，取磨耗功的平均值作为对比分析的依据。

2 驱动方式对走行轮磨耗的影响分析

在直线轨道运行的情况下，对比分析独立驱动和同步驱动两种方式对走行轮磨耗的影响，分别计算得到走行轮的纵向、横向和总磨耗功，结果如图5所示。

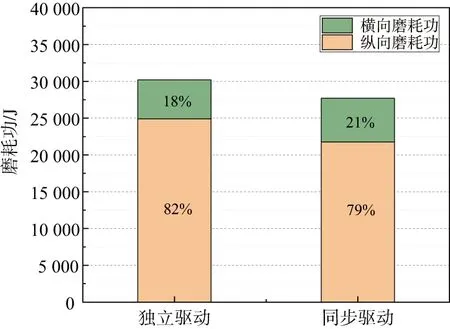
图5 走行轮磨耗功(直线工况)

由图5可知，在直线轨道运行的情况下，独立驱动下走行轮所产生的总磨耗功为30 206 J,同步驱动下走行轮所产生总磨耗功为27 698 J,同步驱动下走行轮磨耗功要明显小于独立驱动下走行轮磨耗功。分析总磨耗功的构成可知，无论是独立驱动还是同步驱动，走行轮的总磨耗功主要由纵向磨耗功构成，其约占总磨耗功的80%，横向磨耗功约占20%。两种驱动方式下横向磨耗功差别不大，总磨耗功的差异主要体现在纵向磨耗功上。这说明走行轮的磨损主要是因为纵向滑移下的摩擦做功所导致，驱动方式对纵向磨耗功产生一定影响，而对横向磨耗功影响不大。

在半径为200 m的曲线工况下，对比分析独立驱动和同步驱动两种方式对走行轮磨耗的影响，计算得到走行轮磨耗功结果如图6所示。

图6 走行轮磨耗功(曲线工况)

在半径为200 m的曲线工况下，总磨耗功主要还是由纵向磨耗功构成，纵向磨耗功约占总磨耗功65%，但横向磨耗功占总磨耗功的比例比直线工况增加，约占35%。独立驱动下走行轮所产生的总磨耗功为27 337 J,同步驱动下走行轮所产生总磨耗功为25 041 J,同步驱动下走行轮磨耗功小于独立驱动下走行轮磨耗功。这说明在直线和曲线工况下，同步驱动走行轮产生的磨耗功均小于独立驱动走行轮产生的磨耗功，驱动方式主要影响纵向磨耗功，对横向磨耗功影响较小。

3 轮径差对走行轮磨耗的影响分析

悬挂式单轨在运行过程中，走行轮会出现不可避免的磨损。为了探究当走行轮已经出现磨损、走行轮的轮之间出现了轮径差、磨耗轮(小轮)与非磨耗轮(大轮)在后续的运行过程中磨损程度的大小，以走行轮同步驱动转向架为例，拟定如图7所示的4种工况。

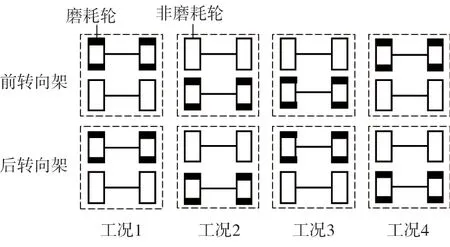
图7 轮径差对走行轮磨耗的工况分析

计算不同轮径差下工况1-工况4各个走行轮的磨耗功，并绘柱状图如图8-图11所示。图中走行轮FFL为前转向架前轮对左轮。符号中第一位F表示前转向架、R表示后转向架；第二位F表示前轮对、R表示后轮对；第三位L表示左轮、R表示右轮。小表示初始存在磨耗的磨耗轮，大表示不存在初始磨耗的非磨耗轮。

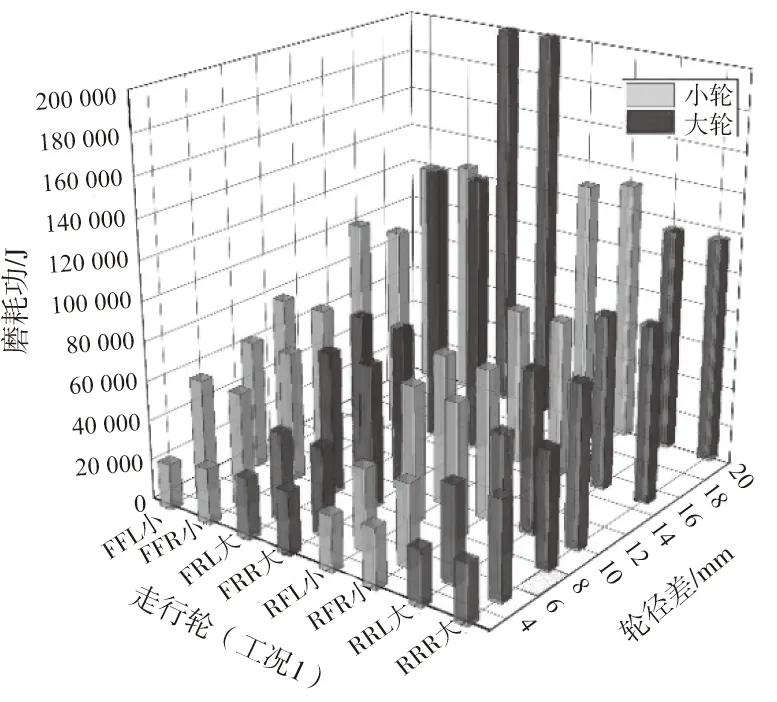
图8 工况1走行轮磨耗功

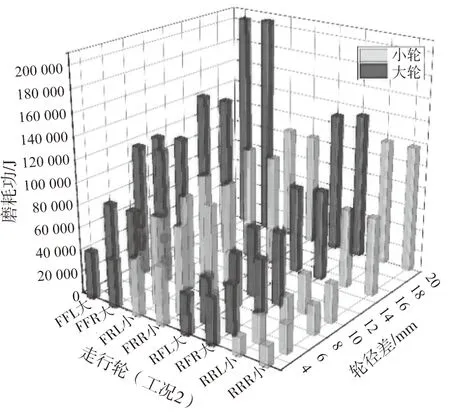
图9 工况2走行轮磨耗功

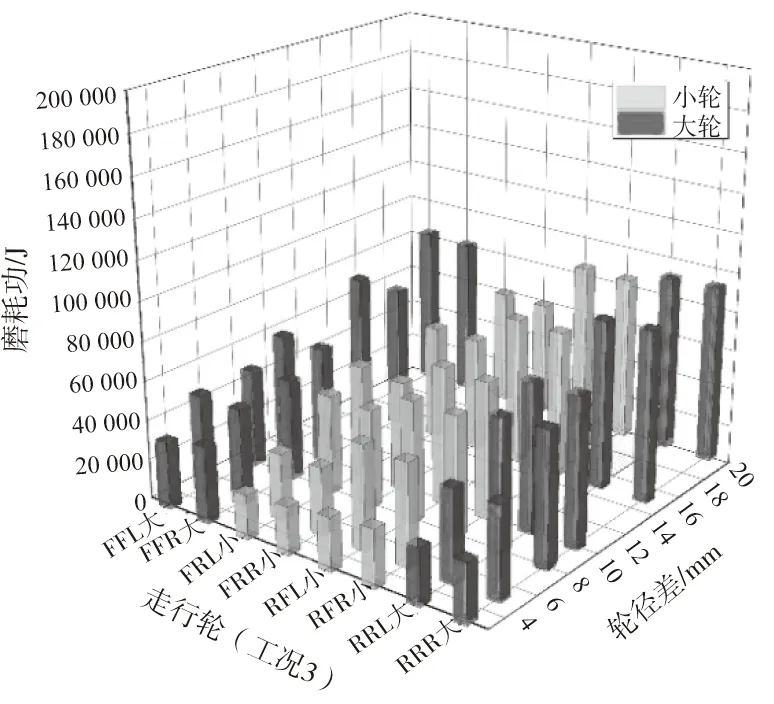
图10 工况3走行轮磨耗功

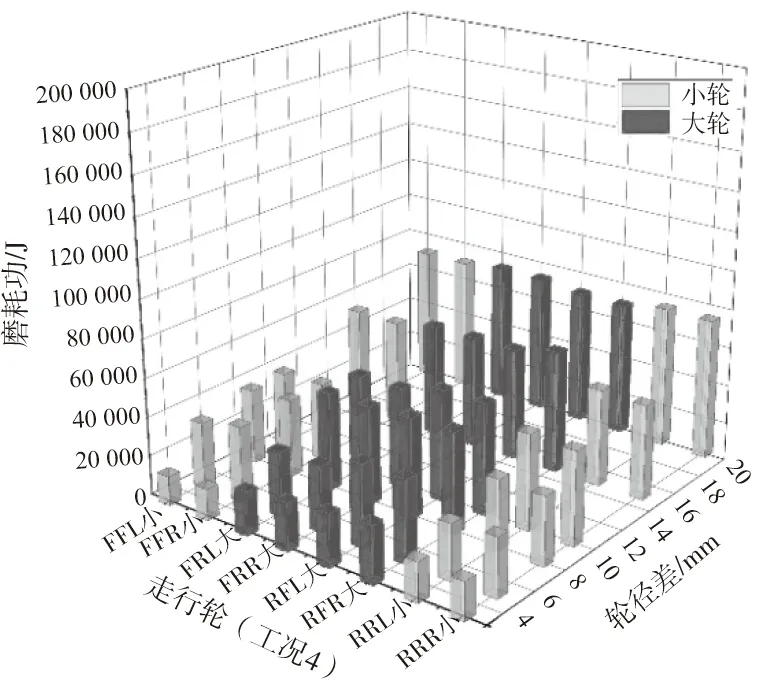
图11 工况4走行轮磨耗功

对比图8-图11中大轮磨耗功和小轮磨耗功的柱状图可知，当走行轮存在轮径差时，在后续的运行过程中，大轮的磨耗功基本都高于小轮。观察走行轮的磨耗功随轮径差的变化可知，轮径差越大，走行轮的磨耗功就越大。对比工况1、工况2和工况3、工况4可知，两个转向架的两个前轮对或两个后轮对出现初始磨耗(工况1、工况2)的工况要比两个转向架的一前一后轮对出现初始磨耗(工况3、工况4)工况的磨耗功要大。这说明轮径差出现在不同的位置也会对走行轮的磨耗功产生不同的影响。

将工况1-工况4的大轮和小轮的磨耗功分别取平均值，得到它们的平均磨耗功随轮径差变化的曲线如图12所示。

图12 磨耗功均值

由图12可以看出，大轮和小轮的磨耗功随着轮径差的增大而增大。大轮的磨耗功大于小轮的磨耗功，且两者之差随轮径差的增大而增大。这个趋势说明当走行轮出现轮径差后，大轮的磨耗比小轮大，大轮的轮径由于磨耗而减小的程度比小轮快，二者之间的轮径差有减小的趋势，走行轮的轮径差不会随着车辆的运行进一步加大。

4 结语

1)走行轮的磨损主要是因为纵向滑移下的摩擦做功所导致，驱动方式主要影响纵向磨耗功。无论是在直线还是曲线工况下，同步驱动下走行轮磨耗功均明显小于独立驱动下走行轮磨耗功。

2)走行轮轮径差的存在会使大轮和小轮磨耗程度不同。当走行轮存在初始轮径差时，在运行过程中大轮的磨耗功基本都高于小轮，且二者的差值随初始轮径差的增大而增大。

3)走行轮出现轮径差后，大轮的磨耗比小轮大，大轮轮径减小的程度比小轮快，二者之间的轮径差有减小的趋势，说明走行轮的轮径差不会随着车辆的运行进一步加大。