基于遗传算法的机器人加工位姿优化研究

王昊，张得礼，王宏涛

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

工业机器人由于其工作灵活、可移动和高重复定位精度等特点被广泛应用于搬运、喷漆、铣削、焊接、制孔等工业加工领域。工业机器人与CNC机床一样具有多轴功能，然而由于工业机器人独特的悬臂梁结构，与CNC机床相比刚度相对较差。CNC机床的刚度通常>50 N/μm[1]，而工业机器人的刚度仅为CNC机床的1/50～1/20，提高工业机器人的刚度对提高加工质量具有重要影响。工业机器人末端刚度由机器人关节刚度和机器人位姿决定[2]，所以对于型号已定的工业机器人，其位姿对末端刚度有着决定性作用。此外，机器人传递力和运动的运动学性能、规避奇异点的能力对机器人的加工性能也有较大影响[3]。国内外学者有关研究表明，可以通过寻优机器人加工位姿达到提高机器人末端刚度性能和运动学性能的目的。CHEN S F等建立了工业机器人末端刚度和关节刚度、机器人姿态的关系，并表明末端刚度随机器人姿态变化而变化[4]；ZARGARBASHI S H H等人提出一种与任务相关的优化方法，对机器人姿态进行寻优，从而选取满足任务要求的最优加工姿态[5]；KHAN W等人基于机器人运动性能评价指标，研究了机器人不同运动性能对机器人加工轨迹的影响[6]。然而上述优化方法仅考虑优化机器人的刚度性能或机器人的运动性能，并没有将二者综合考虑。LIN Y等人在对机器人加工位姿的优化时，对机器人的运动性能和刚度性能皆进行了研究，但其选择优化位姿的方式是在性能分布图中直接选择机器人关节角，未使用优化算法[7]。

本文基于机器人性能指标并结合遗传算法对机器人加工位姿进行优化。

1 机器人运动性能对加工位姿的影响

1.1 机器人正运动学模型

埃斯顿ER30机器人为六自由度关节式工业机器人，且所有关节均为旋转副。按照D-H参数法建立机器人D-H参数模型如表1所示。表1中，关节1-6分别代表机器人的6个关节；θi为关节i的关节角度；di为关节i的偏距，即连杆i-1与连杆i的距离；αi为关节i-1与关节i轴线之间的夹角；ai-1为关节i-1与关节i轴线之间公法线距离。

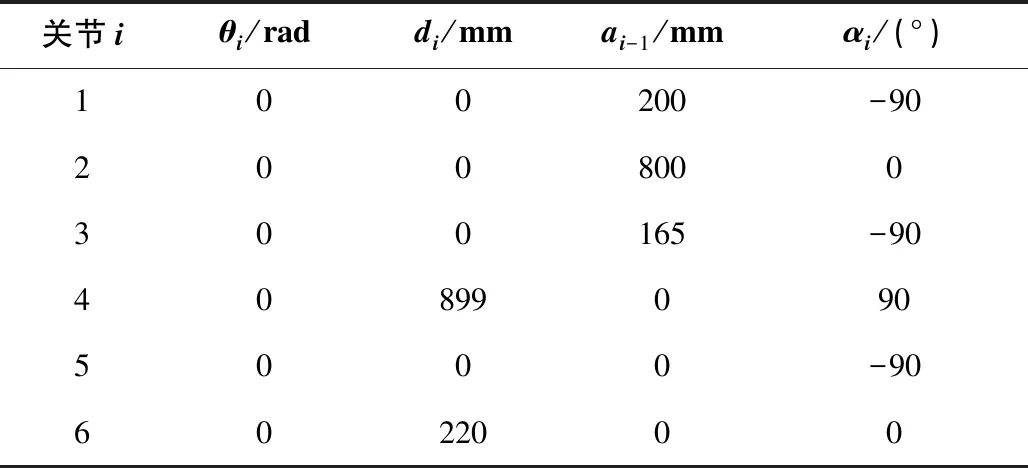
表1 ER30机器人D-H参数

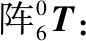
(1)

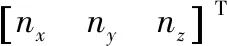
1.2 机器人运动性能评价指标

机器人运动性能是指机器人系统传递力和运动的能力，机器人的运动性能可以通过运动性能指标来评价。机器人运动性能指标除了可以评价机器人的运动性能还可以直观地衡量机器人当前位姿与奇异点距离的远近。本文选择基于条件数[8]的机器人运动性能的评价指标，条件数定义见式(2)，机器人运动性能评价指标KM见式(3)。

(2)

KM=1/K(JN)×100%

(3)

式中：n为雅克比矩阵的维数，本文机器人为6R机器人，所以n=6；tr(JN)为机器人雅克比矩阵的迹；JN为雅克比矩阵的规范标准型。

1.3 各关节角对运动性能的影响

在机器人的6个关节角中，θ1、θ6对机器人末端运动性能无影响[7]，所以设置θ1=0,θ6=0，仅需研究θ2、θ3、θ4、θ5对机器人末端运动性能的影响。式(1)中机器人空间位置px、py、pz主要随θ2、θ3变化而变化，机器人末端姿态n、o、a主要随θ4、θ5变化而变化，所以可通过KM在2、3关节空间中的变化，研究机器人空间位置变化对KM的影响。通过KM在4、5关节空间中的变化，研究姿态变化对KM影响。

为研究θ2、θ3对KM的影响，通过蒙特卡洛法绘制KM在2、3关节空间的分布如图1(a)所示。图1(b)为机器人末端运动性能在笛卡儿空间的分布。在R1、R2、R3三个矩形区域中机器人的末端运动性能较好。通常情况下，机器人进行加工时，待加工工件放于机器人前方，所以当机器人进行加工时，机器人末端通常处在R1区域，此区域内的机器人加工位姿符合加工实际且机器人运动性能较佳，此时θ2∈[-1,0.5]，θ3∈[-0.8,1.5]。

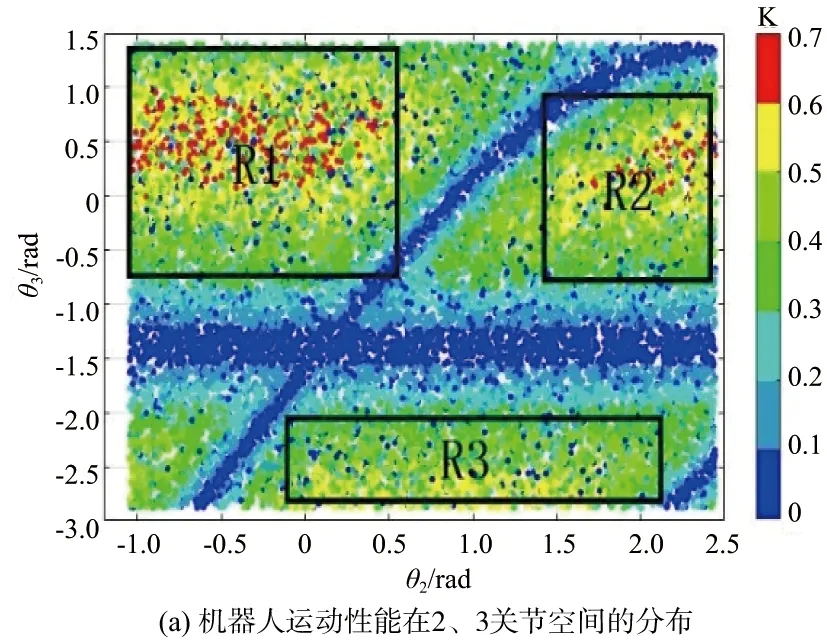
图1 机器人运动性能在关节空间中的分布

同理，绘制KM在4、5关节空间的分布如图2所示。由图2可知，KM主要随θ5变化而变化。在考虑姿态对KM的影响时，只需优化θ5的取值，以避免机器人四轴与六轴平行导致接近奇异点，机器人末端即可达到较好的运动性能。

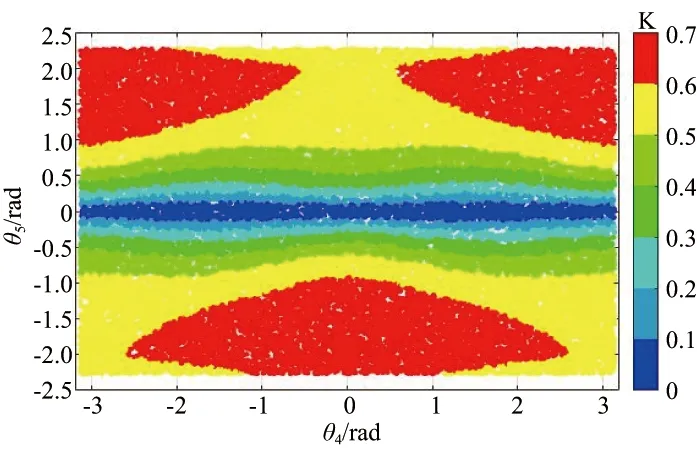
图2 机器人运动性能4、5关节空间中的分布

综合上文分析，当机器人四轴与六轴不平行远离奇异时，θ2、θ3变化导致的KM变化范围为[0,0.7]，θ4、θ5变化导致的KM变化范围为[0.5,0.7]。机器人末端运动性能主要受机器人位置变化即θ2、θ3变化的影响，机器人姿态变化即θ4、θ5变化对机器人运动性能影响较小。

2 机器人刚度性能对加工位姿的影响

2.1 机器人静刚度模型

对于6R串联机器人，加工时其末端误差主要来自于机器人关节的受力变形[9]。基于此可以建立机器人末端笛卡儿刚度矩阵K与关节刚度矩阵Kθ的映射关系[10]：

K=J-TKθJ-1

(4)

式中：J为机器人雅克比矩阵；Kθ=diag([Kθ1,Kθ2,Kθ3,Kθ4,Kθ5,Kθ6])，为机器人关节刚度矩阵。

由式(4)可知，机器人的末端刚度与机器人的雅克比矩阵J和关节刚度矩阵Kθ有关。机器人的雅克比矩阵J仅由机器人位姿决定，所以机器人末端刚度具有位姿依赖性。

2.2 机器人刚度评价指标

为减少计算难度和计算误差，引入机器人柔度模型：

(5)

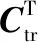
由于机器人末端所受力矩带来的末端变形远小于力带来的末端变形。机器人末端的角位移也远小于线位移，所以机器人刚度性能评价指标Ks可简化为[11]

(6)

2.3 各关节角对刚度性能的影响

由参考文献[7]可知，θ1、θ6对机器人刚度评价指标Ks无影响，设置θ1=0，θ6=0。机器人刚度性能在2、3关节空间的映射如图3所示。对比图3(a)和图3(b)，当θ4、θ5变化时，机器人末端刚度性能在2、3关节空间的分布基本不变。当机器人运动性能较好，即θ2∈[-1,0.5]、θ3∈[-0.8,1.2]时，由图可知，机器人的刚度性能在θ2→0.5，θ3→-0.8时较好。

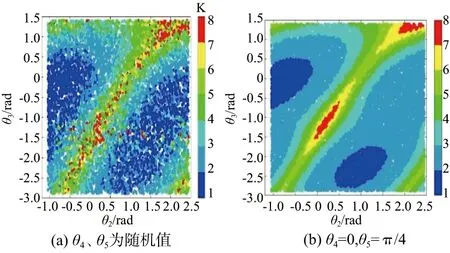
图3 2、3关节空间的机器人末端刚度性能

图4为机器人末端刚度性能在机器人4、5关节空间中的映射。由图4可知，当θ2、θ3为随机值时，机器人刚度性能的分布并无明显规律；θ2、θ3为固定值时，机器人刚度性能分布呈现明显规律，此时Ks取值区间为[2,4]。结合图3，无论θ4、θ5为何值时，机器人刚度性能分布规律不变，Ks取值区间为[1,8]。由此可知θ2、θ3对机器人刚度性能有较大影响，θ4、θ5对机器人刚度性能影响较小，即相较于机器人末端的位置变化，机器人末端的姿态变化对机器人刚度性能影响较小。

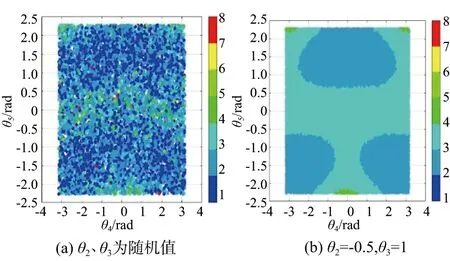
图4 4、5关节空间机器人末端刚度性能

3 基于遗传算法的机器人加工位姿寻优

根据上文的分析，可以归纳得到机器人加工位姿优化问题的数学模型，如式(7)所示。这是一个多目标、多约束且目标数学表达式不可导的优化问题，解决此优化问题需要在变量全局范围内对最优解进行搜索。遗传算法对优化问题没有太多数学要求，其较强的全局寻优能力的特点符合本文优化问题的要求。所以选用遗传算法实现机器人位姿优化。

(7)

1)使用遗传算法寻优机器人加工位姿需先设计变量和适应度函数，设置选择、交叉、变异算子，设置终止条件，步骤如下。

步骤1：设计变量和取值范围。机器人末端运动性能和刚度性能主要受机器人位姿影响，其中θ1、θ6对机器人末端运动性能和刚度性能均无影响，所以待优化变量为θ2、θ3、θ4、θ5。结合上文分析设置各变量取值范围为：

θ2∈[-1,0.5],θ3∈[-0.8,1.2],θ4∈[-π,π],

θ5∈[-2.5，-0.5]∪[0.5,2.5]。

步骤2：设计适应度函数。适应度函数有两个评价指标KM和Ks，以KM和Ks的和作为适应度函数。参考文献[12]考虑到在加工时机器人的运动性能与刚度性能对加工效果都有明显影响，设置权重ω1=2/3，ω2=1/3。最终的适应度函数如式(8)所示。

Fit(θ2，θ3，θ4，θ5)=0.000 1ω1Ks+ω2KM

(8)

步骤3：设置选择、交叉、变异算子。使用轮盘赌选择法对种群中的个体进行选择。为快速淘汰低适应度值的个体，交叉方法为均匀交叉，交叉算子pc=0.8。变异算子pm通常在[0.001,0.1]区间取值，本文变异算子pm=0.05。

步骤4：设置终止条件。遗传算法终止条件有多种，本文以达到目标代数作为终止条件，当迭代代数达到50代时停止优化。

2)完成以上设置后，使用遗传算法对机器人加工位姿进行优化，步骤如下所示。

步骤1：生成初始种群。随机生成符合取值范围的25组关节角θ2i,θ3i,θ4i,θ5i(i=1～25)，并以二进制编码的方式将25组关节角编译成25个染色体作为初始种群。

步骤2：计算Fit。计算初始种群中25个染色体Fit(θ2，θ3，θ4，θ5)。

步骤4：判断是否终止遗传算法。若代数g<50，则g+1，进行步骤5；若代数g>50,则停止优化，输出优化结果。

步骤5：遗传操作生成下一代子群。根据当前种群中各染色体Fit值，对种群中所有个体进行选择、复制、交叉以得到新的种群。进行步骤2。

运行遗传算法得到的优化结果如表2所示。此优化结果对应的机器人位姿如图5所示。优化位姿与随机位姿的性能指标值如表3所示，相较于随机位姿优化后的位姿各项性能得到了较大提升。

表2 遗传算法优化结果(θ1、θ6=0)

图5 优化后的机器人加工位姿

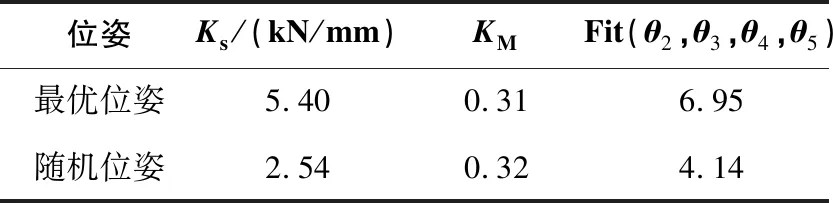
表3 优化位姿与随机位姿的各评价指标值

4 结语

机器人6个关节中，θ2、θ3对机器人运动性能影响较大，θ4、θ5对机器人运动性能影响较小，θ1、θ6对机器人运动性能无影响。当θ2∈[-1,0.5],θ3∈[-0.8,1.2],θ4∈[-π,π],θ5∈[-2.5,-0.5]∪[0.5,2.5]时机器人运动性能较好且机器人位姿符合加工实际。

使用遗传算法对加工位姿进行优化，设计了一种综合机器人运动性能评价指标和机器人刚度性能评价指标的适应度函数，并通过系数设计调整两种性能在优化过程中的比重，最终得到了一个符合加工实际且性能较好的机器人加工位姿。