垂线偏差对高原山区长大隧道横向贯通精度的影响

王 博

(中铁第一勘察设计院集团有限公司，西安 710043)

1 概述

我国高速铁路大规模建设，促进了铁路测量新技术的快速发展。高速铁路大多以桥隧代路，尤其在西部高原复杂山区，长大隧道占比较大，隧道进、出口及各斜井口处大多地势险峻、地形复杂[1]。进洞联系测量时，垂线偏差将直接影响进洞联系测量的方向精度，从而影响最终的横向贯通精度[2]。

在垂线偏差影响规律以及隧道横向贯通精度研究方面，相关学者进行大量研究工作，杨柳根据横向贯通精度的要求，对洞内外控制网进行设计，并对横向贯通误差进行了估算[3]；周亮等分析了隧道洞外、洞内贯通误差影响值的估算方法，但均未考虑垂线偏差的影响[4]；路伯祥等对垂线偏差计算方法进行分析[5]；高佩华等提出在测量设计时需顾及垂线偏差影响的建议[6]；杜传鹏研究垂线偏差等对长大隧道贯通误差影响规律并研制了长大隧道贯通误差分析软件[7]。另外，刘志进行垂线偏差对联系测量的定性影响分析，并提出了构网形式的联系测量方案[8]。在前人研究的基础上，依托某高原山区实验网数据，对某高原山区长大隧道横向贯通精度的影响进行深入研究。

2 垂线偏差的计算方法

求解垂线偏差方法包括天文大地测量法、重力测量法、天文重力测量法和GNSS水准测量法[9]。其中，GNSS水准测量法利用高程异常和垂线偏差间的关系来求解垂线偏差，对于长大隧道平面控制测量是获取垂线偏差的最快捷方法[10]。

GNSS水准测量法测定垂线偏差的方法如下。

(1)分别通过GNSS和水准测量获得基线边两端点A、B间的大地高差和正常高差，从而精确测定该基线两端点的高程异常差，有

Δζ=Δh-ΔH

(1)

(2)垂线偏差在任意垂直面上的投影分量，可由下式计算[11]，有

μ=ξcosA+ηsinA

(2)

(3)则A、B两点间垂线偏差与高程异常差的关系[12]为

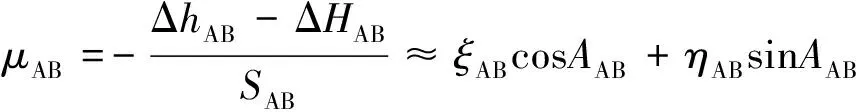
(3)

式中，ξAB、ηAB分别为基线方向AB的垂线偏差μAB在子午圈和卯酉圈上的分量；SAB为基线长度，AAB为沿基线观测方向的大地方位角。

由式(3)可知，在局部区域高程异常差变化不大，即测站小范围内的大地水准面波动较为平稳时，垂线偏差与基线边长度成反比。因此，为减小垂线偏差的影响，进洞联系测量时，后视定向边应尽量选择长边。

(4)对于某一测站点，若存在两条基线边，则垂线偏差计算公式为

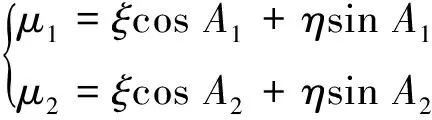
(4)

式中，A1、A2分别为沿基线观测方向的大地方位角。

求解方程组即可获得该测站点的垂线偏差分量ξ和η，有

(5)

3 垂线偏差对隧道横向贯通精度的影响分析

观测方向的垂线偏差改正，即以法线为准的观测方向和以垂线为准的观测方向之间的差别，可由下式计算[13]，有

ΔL=(-ξsinA+ηcosA)tanα

(6)

式中，ξ和η分别为测站点在子午圈和卯酉圈方向上的垂线偏差分量；A和α分别为测站点至目标点的大地方位角和高度角。

由式(6)可知，当α≈0，即基线边两端点大致等高时，垂线偏差对观测方向的影响ΔL≈0，故选择洞外GNSS控制点时应尽量等高。

假设A=0°，α取1°～10°，垂线偏差分量取5″～30″，根据式(6)计算ΔL，计算结果如表1所示。

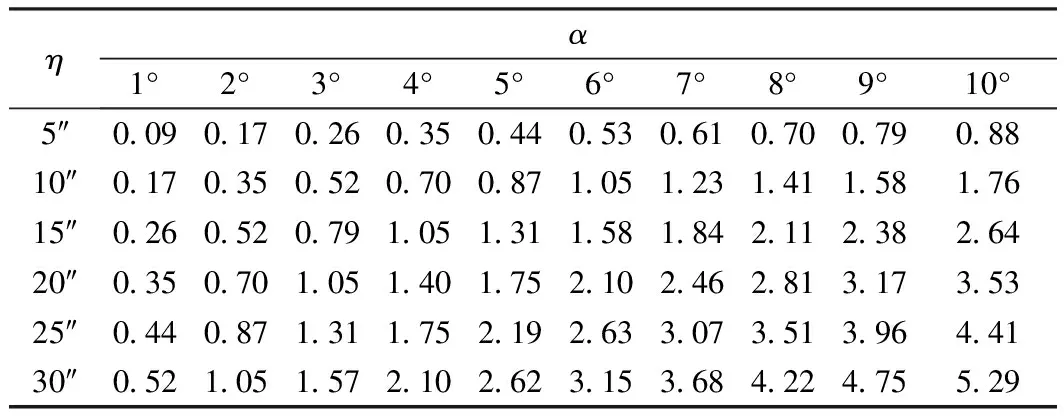
表1 垂线偏差改正计算结果 (″)

由表1可知，与基线边垂线偏差分量以及高度角的大小成正比，基线边高度角一定时，随基线边垂线偏差分量的增大而增大；当在某一局部区域，垂线偏差大小基本一致时，高度角的大小对影响非常明显。垂线偏差对该角度的影响值为

Δβj=(-ξjsinAjk+ηjcosAjk)tanαjk-

(-ξjsinAji+ηjcosAji)tanαji

(7)

由式(7)可知，当三点处于同一高程面时，垂线偏差对角度的影响。对于长大隧道，主洞段各导线点大致等高，故主洞段导线测量基本不受垂线偏差的影响。当斜井为直伸且坡度比较均匀时,,同样有。因此隧道洞内导线测量受垂线偏差的影响可忽略不计。

如图1所示，A、B、C、D为洞外GNSS控制点，1、2、…为洞内导线点，进洞联系测量时以AB为后视定向边，则进洞方向垂线偏差对方向精度的影响反映在角度βA和上。

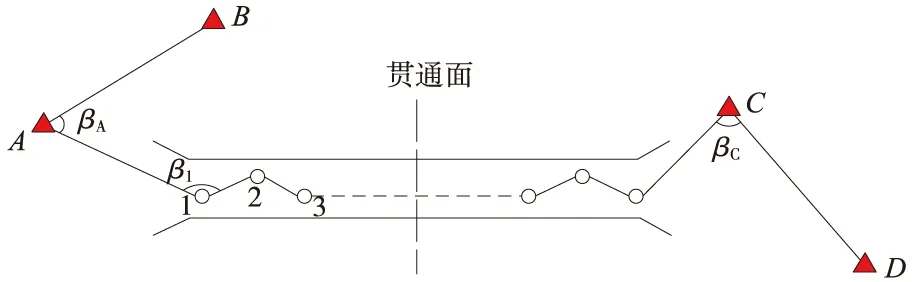
图1 隧道洞内、外引测关系

由式(7)可得，ΔβA=ΔLA1-ΔLAB，Δβ1=ΔL12-ΔL1A；由于在局部区域垂线偏差分量基本相等，由式(6)可知，同一基线边正反方向的垂线偏差改正大小相等，符号相同，即ΔLA1≈ΔL1A。另外，隧道洞内各点高程基本一致，有ΔL12≈0。则进洞方向垂线偏差对方向传递的总影响为

Δ进=ΔβA+Δβ1=ΔLA1-ΔLAB+

ΔL12-ΔL1A≈-ΔLAB

(8)

即垂线偏差对横向贯通误差的影响主要反映在进洞联系测量后视定向边的方向精度上，则垂线偏差对隧道横向贯通误差影响的估计公式为[14]

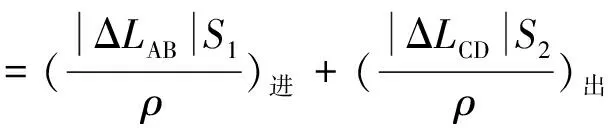
(9)

式中，S1、S2分别为进、出口进洞联系点至贯通面的垂直距离；ΔLAB、ΔLCD分别为进洞和出洞端后视定向边的垂线偏差改正值。

当后视定向边两端点高程基本一致时，垂线偏差引起的横向贯通误差Δ垂线≈0。要减小垂线偏差引起的横向贯通误差，需减小后视定向边的垂线偏差改正ΔL，即增加后视定向边的距离、减小后视定向边的高度角，尽量采用长边、小高差的后视定向边引测方向进洞。此外，由式(9)可知，当ΔL一定时，垂线偏差对横向贯通误差的影响随开挖距离的增大而增大，考虑目前我国长大隧道的现实情况，应将垂线偏差对隧道横向贯通精度的影响作为重点。

4 高原山区垂线偏差实例计算分析

在西部某高原山区(平均海拔4 300 m)，建立全长约14 km的实验网，以模拟长大隧道测量控制网，网形如图2所示。在实验网两端分别布设了1个进洞联系点和2个后视定向点，进洞联系点与后视定向点间的关系分别为短距离大高差和长距离小高差。为模拟长大隧道洞内CPⅡ导线网的情况，每隔400 m左右布设1个控制点(共32个)，所有控制点均埋设强制对中墩。为增加网形强度，测量时在离每个控制点横向方向约10 m处放置1个旁点(临时棱镜点)，构成点对形式。实验网采用工程独立坐标系，以沿线路走向首尾两个进洞联系点JKPA、CKPD的连线为X轴正方向，则Y坐标较差可直接作为横向误差进行对比。对实验网进行GNSS静态相对定位测量(国家C级)、二等导线测量和二等水准测量，GNSS高精度测量成果将作为导线测量成果对比测试的参考基准。

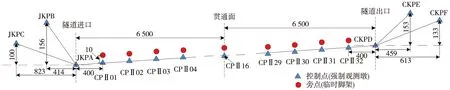
图2 实验网网形示意(单位：m)

根据前述公式，计算各洞外GNSS控制点的垂线偏差分量，结果如表2所示。

由表2可知，进、出口端的垂线偏差分量差异较大，但在局部区域基本一致。根据表2计算成果及观测数据，进一步计算基于不同后视定向边时由垂线偏差引起的横向贯通误差影响值，计算结果如表3所示。

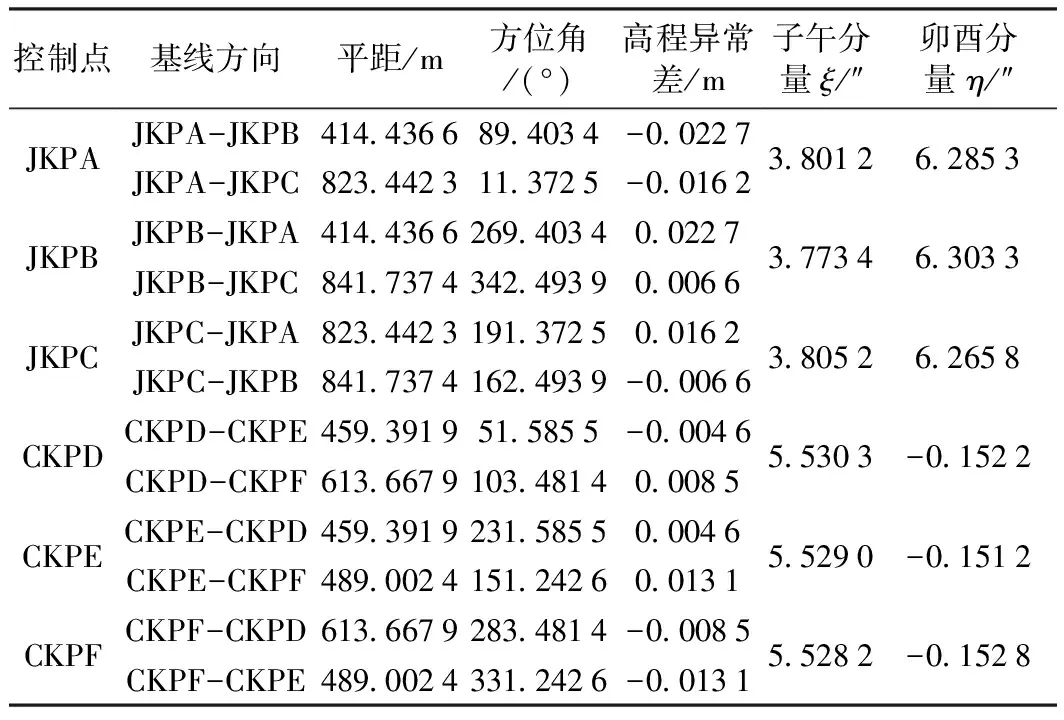
表2 实验网洞外GNSS控制点垂线偏差分量计算

由表3可知，垂线偏差对实验网横向贯通误差的影响非常明显，最大达到46.11 mm。采用不同的后视

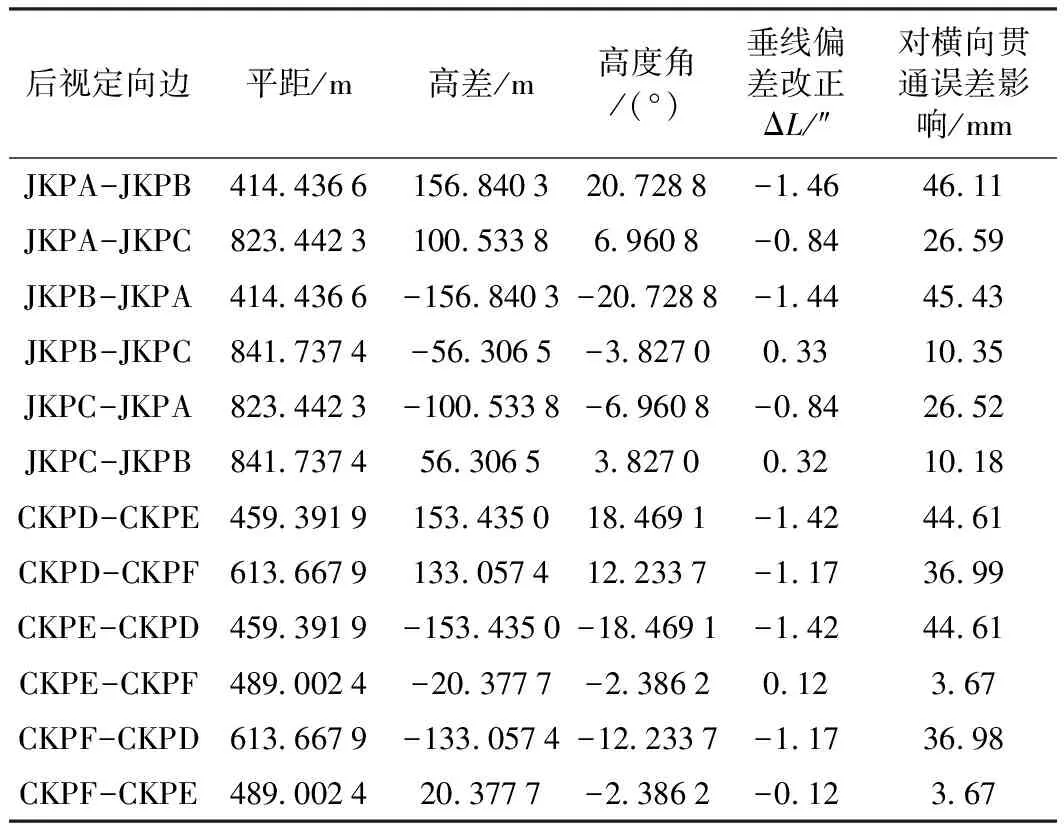
表3 垂线偏差对横向贯通误差影响值的计算

定向边时，垂线偏差对横向贯通误差的影响差异极大(若以CKPE-CKPF为后视定向边，则垂线偏差对横向贯通误差影响值仅为3.67 mm)，说明后视定向边的选择对横向贯通误差影响极大。

以实验网GNSS观测结果作为真值，将导线测量的贯通点(CPⅡ16)坐标与之对比，为验证垂线偏差的影响，对比方案作如下设计。

方案一：进出口分别采用短边、大高差的后视定向边(JKPA-JKPB、CKPD-CKPE)，不进行垂线偏差改正。

方案二：在方案一的基础上加垂线偏差改正。

方案三：进出口分别采用长边、小高差的后视定向边(JKPA-JKPC、JKPD-JKPF)，不进行垂线偏差改正。

方案四：在方案三的基础上加垂线偏差改正。

基于上述4种方案，对至贯通点的Y坐标及与GNSS测量的Y坐标成果较差以及横向贯通误差进行统计，结果如表4所示。

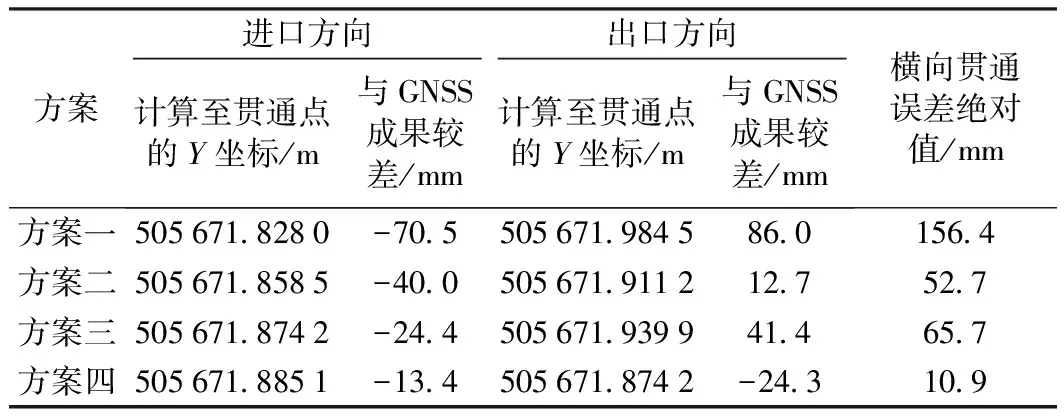
表4 横向贯通误差比较

由表4可知，采用长边、小高差的后视定向边计算的横向贯通误差(65.7 mm)明显优于采用短边、大高差的后视定向边的计算结果(156.4 mm)。进、出口分别采用同样的后视定向边，加垂线偏差改正后(方案二、方案四)计算的横向贯通误差明显优于加垂线偏差改正前(方案一、方案三)的计算结果。方案四在采用长边、大高差的后视定向边的基础上，添加垂线偏差改正，计算的横向贯通误差最优，仅为10.9 mm，说明采用长距离、小高差的后视定向边并添加垂线偏差改正对提高最终的横向贯通精度作用明显。

在进行隧道洞外控制网设计时，应慎重考虑洞外各控制点的相对位置关系，尽量使各控制点处于同一高程面以避免垂线偏差对隧道横向贯通精度造成较大的影响。在高原复杂山区地形条件下，受客观条件的限制，洞外各控制点往往无法满足基本等高的条件，而山区地形起伏过大，容易产生较大的垂线偏差，故控制网设计时后视定向边应尽量设计成长边、小高差，控制网精度估算时应考虑垂线偏差的影响，测量时应对全站仪观测数据加垂线偏差改正。

现行规范中[15]，控制网精度估算时仅顾及洞外GNSS和洞内导线网引起的隧道横向贯通中误差，并未考虑垂线偏差的影响，这对高原复杂山区长大隧道控制网的精度控制不利。高原山区地形条件复杂，一般难以选取到最优的后视定向边方案，故在进行控制网精度估算时，应以最不利情况进行估计，在顾及垂线偏差影响时，隧道横向贯通误差为

(10)

式中，m洞内、m洞外分别为洞内外控制测量误差对横向贯通误差影响值中误差。

5 结论

(1)在高原山区复杂地形条件下进行长大隧道贯通控制测量时，垂线偏差对隧道横向贯通精度的影响不可忽略，且影响值随开挖距离的增大而增大。

(2)垂线偏差对横向贯通精度的影响主要反映在进洞联系测量后视定向边的方向精度上。控制网设计时，应对洞外GNSS控制点的布设位置进行重点设计，后视定向边应尽量设计成长边、小高差，以减小垂线偏差的影响。

(3)添加垂线偏差改正对导线测量横向贯通精度增益明显，高原山区长大隧道测量时，应对后视定向边添加垂线偏差改正。