考虑平衡气体效应的斜爆轰波驻定窗口的研究

张镭潆,归明月,张雨桐,崔 皓,张 辉

(南京理工大学 瞬态物理重点实验室,江苏 南京 210094)

高超声速飞行技术是以吸气式及其组合式发动机为动力,在大气层或跨大气层以马赫数大于5的速度远程巡航飞行,该技术可以应用于高超声速巡航导弹、高超声速飞机和空天飞机等新型飞行器,因而引起国内外广泛的关注[1]。斜爆轰发动机应用于高超声速飞行,具有结构简单、体积小、能量利用率高等优点[2-3],成为研究的热点。

在障碍物作用下,高超声速的可燃气流可形成驻定于障碍物的爆轰波,据此原理设计的发动机称为驻定斜爆轰发动机。过去的几十年,针对斜爆轰现象已经进行了大量的实验研究[4-8]、数值研究[9-16]和理论研究[17-21]。这些研究主要集中于爆轰波的结构和爆轰波的驻定特性,本文将针对后一种情况展开研究。由于斜爆轰波可以认为是斜激波与燃烧的耦合,燃烧释放的能量使斜爆轰波的极曲线较斜激波萎缩,即驻定于斜劈的斜爆轰波的形成受到很大限制,较斜激波困难得多。PRATTT等[17]理论推导了斜爆轰波的极曲线关系式,并首次提出了驻定窗口的概念。EAMNUEL等[18,20]从理论上证明了流动偏转角(斜劈角)θ小于CJ爆轰对应的最小角度θCJ时,斜爆轰波后Taylor波的存在可以维持斜爆轰波的自持。这些分析均是基于一步反应的化学模型。伍智超等[21]对考虑了真实气体效应的极曲线进行了分析,对一组非线性方程组进行求解,得到了不同情形下的极曲线,然而,该方程组无法对极曲线进行定性讨论。

在真实的飞行状况下,随着飞行条件的不同,爆轰强度发生相应的变化,导致化学平衡的移动和平衡组分的变化,即平衡气体效应,此时,波后化学反应的释热量不同,进而斜爆轰波的强度也发生变化,以往的研究没有考虑到这种效应。本文基于考虑平衡气体效应的斜爆轰波的极曲线关系式,采用迭代算法,绘制了斜爆轰波的极曲线和驻定窗口,并讨论了不同的来流参数对驻定窗口的影响,比如来流速度、初温、初压和混合物的当量比等。

1 斜爆轰波极曲线的理论推导

高超声速可燃气流经过角度为θ的斜劈时,在其壁面形成驻定斜爆轰波,如图1所示。

图1 角度为θ的斜劈形成的斜爆轰波的示意图

在斜爆轰波的波阵面建立质量守恒方程、切向和法线的动量守恒方程、能量守恒方程。

质量守恒方程:

ρ1u1n=ρ2u2n

(1)

法向动量守恒方程:

(2)

切向动量守恒方程:

(ρ1u1n)u1t=(ρ2u2n)u2t

(3)

能量守恒方程:

(4)

式中:下标1和2分别代表斜爆轰波前和波后的状态,ρ为混合气体密度,un和ut分别为混合气体速度在斜爆轰波阵面法向和切向的速度分量,p为混合气体压力,h为混合气体的焓。

气体的焓h可以表示为标准生成焓h0和显焓,即:

(5)

利用式(1)～式(5),可得到斜爆轰波角β和斜劈角θ(流动偏转角)间的关系,即斜爆轰波的极曲线[22]:

(6)

式(6)中等号右边分子中“-”代表过驱爆轰,“+”代表弱欠驱爆轰。Ma1n为斜爆轰波前气流的马赫数在法向方向的分量,γ为混合气体的比热比,c1为斜爆轰波前气流的声速,Q为反应热,wk为混合气体中的第k组分的质量分数,hk为混合气体中的第k组分的生成焓。

在方程(6)中,爆轰波后的比热比γ2、反应热Q与爆轰波后的平衡成分有关,是未知量,计算时需要预先给定初值,因此方程(6)无法直接求解。本文采用迭代算法,求解的过程如下:

①爆轰波后的比热比γ20和反应热Q的初始值采用CJ爆轰波后的平衡成分计算比热比γCJ和QCJ,随后,根据斜爆轰波前后关系式和极曲线关系式得到波后的参数p2、ρ2、h2、u2和斜爆轰波角β;

②根据波后的压力p2和温度T2,利用计算平衡组成的代码CEA,得到爆轰波后的平衡组分和比热比γ2;

③将计算得到的比热比γ2与预先设定的比热比γ20进行比较,按照收敛判据|γ2-γ20|<1.0×10-6,如不收敛,再次进入第①步和第②步计算,直到收敛。

爆轰波极曲线迭代求解的具体流程如图2所示。

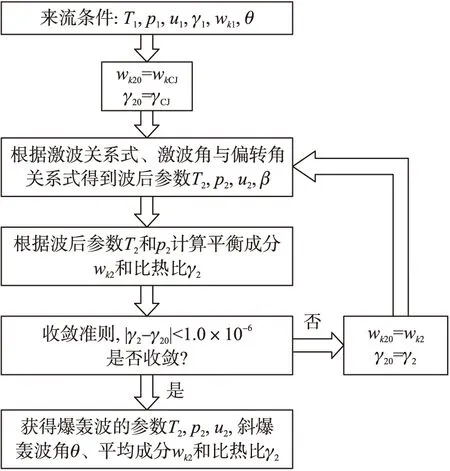
图2 求解过程流程图

2 斜爆轰驻定窗口及其影响因素

2.1 爆轰波后参数随爆轰波强度的变化

考虑真实气体情形时,涉及到多种组分和多步化学反应,对于一定的温度和压力,化学反应最终会达到平衡状态,反应系统具有不变的组分。当来流速度发生变化时,爆轰强度随之变化,化学平衡发生偏移,平衡系统的组分和热效应都将随之变化,即方程(6)中的反应热Q和波后的比热比γ2亦发生变化。因此,不同强度的爆轰波对应不同的反应终态及相应的流场参数。

对于初温为298 K,初压为101.325 kPa的氢气-空气的混合气体,考虑平衡气体效应。该温度气体包含9种组分:H2、O2、H、O、OH、HO2、H2O2、H2O、N2。当斜劈角θ=0°时,方程(1)～方程(5)描述的是正爆轰,此时,可以用来流马赫数代表爆轰波的强度,分别绘制爆轰波后压力、温度、燃烧产物H2O质量分数(w(H2O))、平衡成分的比热比、反应热等参数随来流马赫数的变化,见图3。随着来流马赫数增加,爆轰波强度增加,波后的温度和压力也相应增加,如图3(a)和3(b)所示,达到化学平衡时,燃烧产物H2O的质量分数呈下降趋势,如图3(c)所示,这与复杂的基元反应有关。平衡成分的比热比则呈增加的趋势,如图3(d)所示,这是由于气体的比热比与基本粒子的自由度有关,自由度越小,比热比越大。随着爆轰波强度的增加,自由度较大的三原子分子的浓度下降,比如H2O,故平衡成分的比热比变大。同时,反应热Q变小,如图3(e)所示,这是由于随着爆轰波强度增加,平衡向自由基和离子增多的方向移动,故反应热随之下降。

图3 爆轰波后不同参数随马赫数的变化

2.2 斜爆轰波驻定窗口及影响因素

当来流的马赫数为9时,根据方程(6),绘制爆轰波极曲线,如图4所示,方程(6)的分子中的“-”号对应的曲线是图中实线,代表过驱爆轰,“+”号对应的曲线是图中虚线,代表弱欠驱爆轰,这部分违反热力学第二定律,属于不存在的区域。当方程(6)中的变量N=0时,有唯一解,即实验中观察到的CJ爆轰,图中在过驱爆轰和欠驱爆轰的交点,对应的流动偏转角为θCJ。对于过驱爆轰,最大的流动偏转角θmax为斜爆轰波脱离斜劈的角度,该角度将过驱爆轰分为上下两部分:强过驱爆轰和弱过驱爆轰。由于弱过驱爆轰的熵增较小,因此,实际爆轰过程中出现的往往是这部分,也称为斜爆轰波可以驻定的区域[θCJ,θmax]。根据方程(6),绘制不同来流马赫数对应的斜爆轰极曲线,如图5(a)所示,由图可见,随着来流马赫数的增加,斜爆轰波越强,相应的驻定区域[θCJ,θmax]越大,将这些区域连接,可构成斜爆轰波的驻定窗口,如图5(b)所示。

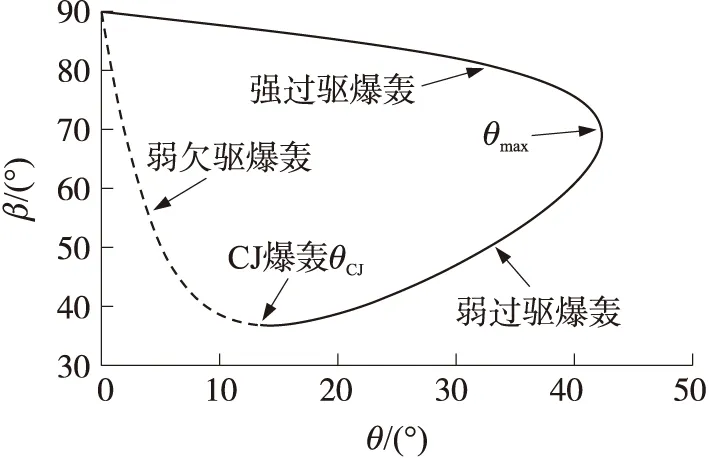
图4 等当量比氢气-空气混合物在Ma=9时的爆轰极曲线(T1=298 K,p1=100 kPa)

图5 等当量比氢气-空气混合物的斜爆轰驻定窗口(T1=298 K,p1=100 kPa)

为了更加清晰地描述平衡气体效应对斜爆轰驻定窗口的影响,本文将平衡气体效应(多组分)与一步反应(双组分)的斜爆轰波极曲线进行比较。一步反应的热力学参数取自文献[23],该参数是国外研究者研究爆轰较多采用的热力学参数,其具体值为:比热比γ=1.17,反应热Q=43.28RT0/M,摩尔质量M=21 g/mol,活化能Ea=46.37RT0。图6为考虑平衡气体效应的多组分与一步反应的双组分的氢气-空气混合物的斜爆轰驻定区域的比较。图6(a)为2种情况斜爆轰极曲线的比较。由图可观察到的驻定区域更大。按照图5的方法绘制不同来流马赫数对应的驻定窗口,可得图6(b),由图可见,考虑平衡气体效应的斜爆轰波的驻定窗口更大。出现这种差异的原因是由于一步反应体现的是反应的总体效应,且反应前后的比热比为常数,无法反映不同斜激波的波后温度对斜激波的影响,故得到的斜爆轰波的强度相对较弱,而考虑平衡气体效应时,斜爆轰波后的平衡气体中的比热比是随着波后温度(来流马赫数越大,波后温度越高,见图3(b))的增加而增加,如图3(d)所示,因此,计算得到的斜爆轰波强度较大,故其驻定窗口也越大,也更加接近真实的飞行情况。

图6 考虑平衡气体效应和一步反应的斜爆轰驻定窗口的比较

斜爆轰波的驻定受多种因素的影响,比如飞行马赫数、可燃混合物的初温、初压、当量比(φ)等。图5描述了飞行马赫数对斜爆轰波驻定窗口的影响,在讨论混合物初温、初压和当量比对驻定窗口的影响时,均采用飞行马赫数为9,相应的计算结果如图7～图9所示。

对于等当量比的氢气-空气预混气,当初始压力为100 kPa时,斜爆轰波的驻定窗口随不同初始温度的变化如图7所示,初始温度越高,爆轰波驻定区域越大,即爆轰波越容易驻定。当混合物初温为298 K时,斜爆轰波的驻定窗口随不同初始压力的变化如图8所示,初始压力对驻定窗口的影响不大,这主要是由于初始压力对化学平衡的影响不大,使得波后的比热比和反应热受压力的影响有限。当混合物的初始压力为100 kPa,初始温度为298 K时,斜爆轰波的驻定窗口随不同氢气-空气混合气体的当量比的变化如图9所示,混合气体的当量比越小,即气体处于富氧状态时,爆轰波越容易驻定。

图7 斜爆轰波驻定窗口随初温的变化

图8 斜爆轰波驻定窗口随初压的变化

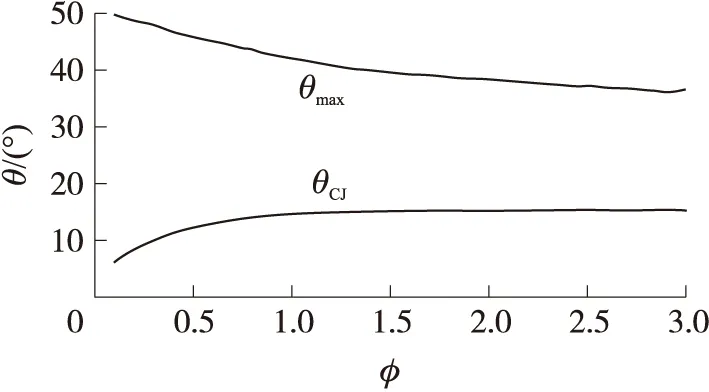
图9 斜爆轰波驻定窗口随混合物当量比的变化

3 结论

考虑平衡气体效应的斜爆轰波的极曲线关系式,采用迭代算法,分析了斜劈诱导的斜爆轰波的驻定特性,得出如下结论:

①对于正爆轰,考虑平衡气体效应时,随着爆轰波强度的增加,波后压力、温度和比热比均增加,而爆轰产物H2O的质量分数和反应热下降。

②与一步反应相比,考虑平衡气体效应时,波后平衡气体的比热比会随着爆轰波强度的增加而增加,因此,形成的驻定窗口也较大,更符合真实的飞行状况。

③斜爆轰波的驻定受不同因素的影响,飞行马赫数、混合物初温和当量比影响较大,初压影响较小,其中飞行马赫数和混合物初温越大,驻定窗口越大;混合物的当量比越小,驻定窗口越大。