基于特征增强和优化SVM的工控入侵检测

黄一鸣，赵国新，魏战红，刘 昱

(北京石油化工学院 信息工程学院，北京 102617)

0 引 言

随着ICS网络的开放、工控协议的通用化以及“震网”等病毒的活跃，工控系统面临着严重的安全威胁，亟需有效解决方案[1]。作为重要的信息安全防护手段，入侵检测的研究成为工控信息安全领域的一个热点[2]。

入侵检测本质是对异常数据和正常数据进行分类[3]。SVM作为一种高效的学习方法，在构建入侵检测系统时表现优秀[4]。SVM的分类性能受惩罚参数c和核函数参数g的选取影响极大[5]。粒子群优化算法(particle swarm optimization，PSO)参数少、易于实现，被广泛应用到SVM参数寻优中[6]。王华忠等[7]将PSO-SVM与PCA相结合应用于工控入侵检测中，不仅提高检测精度也大幅缩短训练时间。陈东青等[8]改进了KPSO算法，提出了基于MIKPSO-SVM的入侵检测框架，并使用标准工控入侵检测数据集验证，取得了良好的效果。

输入数据质量同样影响入侵检测性能[9]。对输入数据进行转换或重构对于入侵检测[10]具有重要意义。常用的转换方法如主成分分析(PCA)和线性判别分析(LDA)忽略了部分特征所包含的分类信息，具有一定有局限性的。Fan等[11]提出了对数边际密度比变换(logarithm marginal density ratios transformation，LMDRT),充分利用特征所包含的信息，提高了数据质量。

本文通过LMDRT增强了输入工控数据质量，并针对粒子群算法易陷入局部最优等问题，使用种群聚集程度指导权重自适应变化优化粒子搜索能力，结合粒子重构策略提高种群跳出局部最优能力，改进了粒子群算法，并用于SVM工控入侵检测模型的优化与构建。用密西西比大学(MSU)标准工控入侵检测数据集进行模型检测，验证了该方法在提高检测精度与效率的优越性。

1 对数边际密度比变换

对数边际密度比变换是Fan等[11]提出的一种非参数数据转换方法。由于边际密度比被认为是最强大的单变量分类特征，LMDRT充分利用各个特征所包含的分类信息，变换后的数据具有更高的数据质量和更优的分类性能。其原理如下：

假设(A,B)是一组已标记样本，其中A=(a1,a2…,aT)∈RT表示特征量，B∈{0,1}表示类别标签。分类器h 表示样本从特征空间到类别标签的数据依赖映射。其构造目的通常是为了最小化风险P (h (A)≠B)。设类别0与类别1的条件概率密度分别为g(A)和f(A)，即(A|B=0)～g 和(A|B=1)～f。根据贝叶斯决策规则有I(r (a)≥1/2)，则

(1)

为简化式(1)，可设P (Y=1)=0.5，则分类的决策边界为

{a:f(A)/g(B)=1}={a:log f(A)-log g(B)=0}

(2)

设gj(aj)和fj(aj)分别为g(A)和f(A)第j个特征的边际值，即特征空间A各个特征的边际密度。根据朴素贝叶斯模型的假设理论，给定类别的各个特性的条件分布相互独立,则有

(3)

由于边际密度比被认为是最强大的单变量分类器，因此新变换的数据充分利用了原始数据中包含的分类信息，且充分考虑了每个特征所表现出的类别差异。因此，可以认为LMDRT是对原始特征最强大的转换，这将显著提高原始数据的质量。同时，线性分类问题的决策边界不再是原始特征的线性组合；而是如下式所示的非线性形式

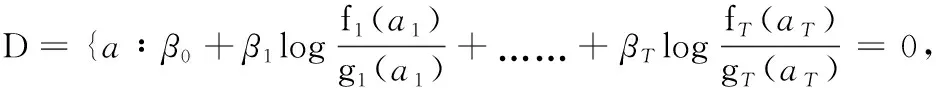
(4)

由于各个特征的边际密度gj和fj未知，需要其进行估计，这里采用非参数核密度估计法对其进行计算。LMDRT的详细过程如下。

假设有N个已被标记类别的样本，S={(Ai,Bi),i=1,2,…,N}，其中Ai∈RT表示特征量，Bi表示数据类别标签。

(1)数据拆分

将S随机拆分为互斥的两部分S1和S2。记S1=(A(1),B(1)),S2=(A(2),B(2)),N1和N2分别记为S1和S2样本的数量。

(2)类条件概率密度的核估计

(5)

(6)

(3)数据转换

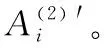
(7)

LMDRT具体流程如图1所示。

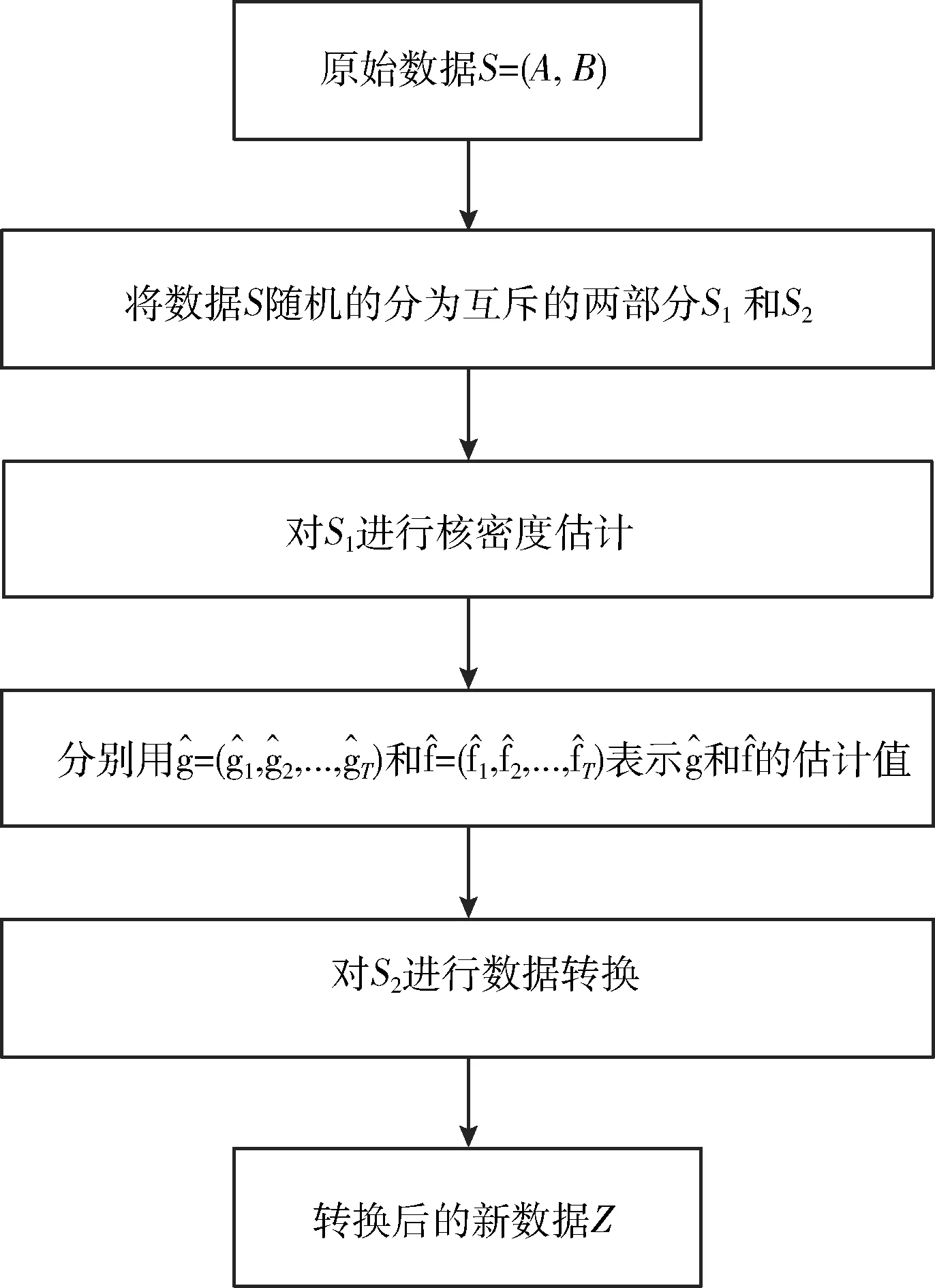
图1 对数边际密度比变换流程

2 改进粒子群算法

2.1 粒子群算法

粒子群优化算法(particle swarm optimization，PSO)的相关定义请参见文献[12]，其简要原理如下：

对于n维空间中包含m个粒子的粒子群，其每个粒子位置Di=(αi1,αi2,…,αin)与速度Vi=(βi1,βi2,…,βin)依据迭代中每个粒子历史最佳适应度位置Li=(li1,li2,…,lin)和全体粒子历史最佳适应度位置Lgbest=(lg1,lg2,…,lgn)。对每个粒子速度和位置进行更新，公式如下

(8)

(9)

虽然粒子群算法易于实现且可操作性强但其依旧存在寻优稳定性差、算法收敛精度低且易陷入局部最优等问题，本文针对其存在的问题做出如下改进。

2.2 改进的PSO算法

2.2.1 粒子初始位置改进

为保证种群均匀分布，本文使用佳点集法确定粒子初始位置以避免初始种群聚集度过高[13]。其原理如下：GS是S维欧式空间的单位立方体，GS中的点r=(r1,r2,…,rS)，满足

Pn(k)={({r1k},{r2k},…,{rSk})，1≤k≤n}

(10)

其偏差为φ(n) = C(r,ε)n-1 + ε， C(r,ε)为一常数且只与r和ε有关，则称r为佳点，Pn(k)为佳点集。为满足上述条件通常取

r={2cos(2πk/p),1≤k≤n}

(11)

式中：p为满足(p-3)/2≥S的最小素数。

在种群规模一定情况下，佳点集的取点比随机取点更均匀，更具多样性且更稳定，其在搜索空间中的映射作为初始种群更具遍历性，更有助于全局最优点的寻找，且具有更好的寻优稳定性。

2.2.2 惯性权重的改进

对于粒子群算法而言，惯性权重w用以平衡种群的全局搜索和局部搜索能力，w越大种群全局搜索能力越强，w越小种群局部搜索能力越强。w通常的调整策略是随着迭代次数递减，以获得较好的收敛性能。但该方法忽略了个体在更新进化过程对权重的调整需求。事实上，个体间的聚集程度可以作为w调整的依据。在粒子群进化过程中，前期多数个体与最优个体聚集程度低，则需要较高的权重，以提高种群的全局搜索能力，后期个体与最优个体的聚集程度高，则需要较低的权重，以获得较好的局部搜索能力。

本文引入曼哈坦距离[14](Manhattan distance)来评估个体间的聚集程度，从而指导w的调整，距离计算公式如下

(12)

式(12)表示粒子i到粒子j的距离，其中，粒子i在n维空间表示为Xi=(xi1,xi2,…,xin)，f 表示粒子适应度值。记种群有N个粒子，则粒子间平均距离有

(13)

则粒子自适应惯性权重调整方法如下

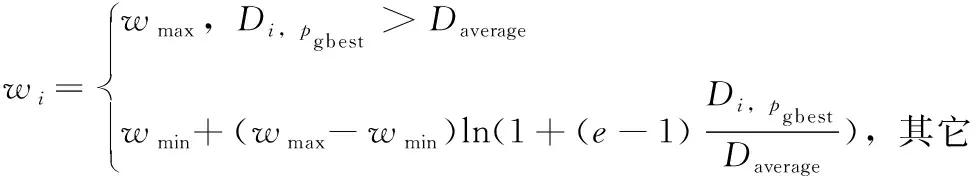
(14)

式(14)表示粒子i的惯性权重，pgbest表示当前迭代的全局最优位置，wmax和wmin为惯性权重的上下限，根据文献[15]分别为0.9和0.4。

2.2.3 粒子位置更新的改进

由于粒子群算法后期种群的聚集度增高，多样性降低，使种群难以跳出局部最优点。为解决这一问题，本文采用粒子重构的方法，让适应度较差的粒子向适应度较好的粒子学习进而生成新的粒子来替代适应度较差的粒子。其过程如下。

首先对种群中粒子的按适应度值进行排序，适应度差的前Np个粒子记为重构对象，剩余粒子记为学习对象。Np值由下式确定

Np=round(0.8Nt/T)

(15)

式中：N表示种群总粒子数；t表示当前迭代数；T表示总迭代数。由于粒子多样性随迭代次数呈下降趋势，因此重构个体随迭代逐渐增加。根据文献[16]，重构对象最多为种群的80%。

对重构对象Xp=(xp1,xp2,…,xpn)的每一维度，随机选取一个学习对象Xg=(xg1,xg2,…,xgn)，同时生成一个决策参数Ppj,(j=1,2,…,n)，Ppj为分布在区间[0,1]上的随机数。粒子重构方法如下

(16)

式中：x′pj为重构后第j维的值，Pc是学习概率，设置为0.8。

下面是结合自适应权重和粒子重构策略的粒子群优化算法的执行步骤：

步骤1设置种群规模、个体维数以及最大迭代次数。根据佳点集(式(10)、式(11))在搜索空间中的映射初始化粒子群；

步骤2计算粒子适应度，进行种群每个粒子间适应度对比记录全局最优适应度位置，进行粒子旧位置与新位置对比记录个体最优适应度位置；

步骤3使用式(12)、式(13)分别计算种群中每个粒子与全局最优位置的距离和种群平均距离，使用式(14)确定每个粒子的惯性权重；

步骤4 将惯性权重带入式(8)、式(9)来更新粒子的速度与位置；

步骤5 按适应度排序粒子，低适应度粒子按式(15)、式(16)进行重构；

步骤6 若未满足设定的结束则重复执行步骤2～步骤5直至达到设定最大迭代数。

3 基于特征增强数据和优化SVM的工控入侵检测算法模型

3.1 SVM算法

支持向量机的定义请参见文献[17]，其基本原理如下。

SVM求解问题可视为在原空间上求解一个二次规划问题

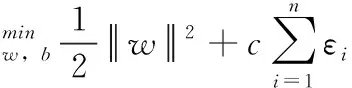
(17)

式中：c为惩罚参数，表示对错误分类的惩罚程度。εi为松弛变量。利用拉格朗日乘子法，式(15)可改写为

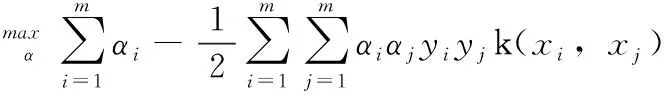
(18)

式中：αi拉格朗日乘子，k(，)为核函数。本文中使用高斯核函数，即

(19)

本文使用LMDRT对原始数据进行数据质量的提升，并通过改进的粒子群算法对SVM的c和g的寻优。此外，由于LMDRT和传统SVM都是针对二分类问题，因此采用一对一的方式(one-oversus-one)构建k(k-1)/2个分类器，采用投票法实现工控网络入侵攻击的多分类。

3.2 构建相关入侵检测模型

基于LMDRT增强后数据和AWPRPSO-SVM的工业控制系统入侵检测模型构建流程如图2所示。

图2 入侵检测模型构建流程

入侵检测模型构建过程分为3个阶段：

(1)预处理：将数据集划分为辅助变换数据S1和被变换数据S2进行LMDRT变换；将变换后数据Z划分为训练集和测试集并进行归一化处理。

(2)SVM参数寻优：将SVM的参数c和g作为优化的对象，使用训练集对SVM模型进行训练。选取5折交叉验证下的分类准确率的相反数作为适应度，利用AWPRPSO算法迭代寻找到最优的SVM参数。

(3)模型测试：将优化后参数c和g带入并构建对应的SVM分类模型，使用LMDRT变换后的数据对模型进行验证。

4 实验结果与分析

4.1 数据集

本文使用的标准工业控制系统入侵检测公开数据集由美国密西西比州立大学提供，研究人员通过采集天然气管道控制系统网络层数据，记录并整理了8种攻击数据(包括正常数据)，每条数据包含26个属性特征和一个攻击类别标签，每种攻击形式、说明及对应类别标签见表1。

表1 攻击形式说明及对应标签

4.2 预处理

LMDRT：从原始数据集中随机且均匀地选取16 000组数据用于数据读数边际密度比变换，均匀地选取其中10 000组作为辅助变换数据，余下6000组变换后用于后续仿真。

4.3 仿真参数的设定

本文所有的算法与模型均进行了相应仿真测试实验，仿真实验平台如下：Inter Core i7-8565U 1.80 GHz，8 GB内存，Windows 10，MATLAB R2016b。随机且不放回抽取数据集中数据，按标签比例划为辅助变换数据10 000条、训练数据4000条和测试数据2000条。AWPRPSO算法相关参数设定如下：种群规模为20，最大迭代次数50，搜索维数为2，加速因子c1和c2分别为1.6和1.5，惯性权重上下限分别为0.9和0.4，粒子重构中学习概率为0.8。本文中其它算法的最大迭代次数、群体规模、搜索维数和加速因子都和AWPRPSO算法相同，惯性权重固定为0.8。使用优化算法对SVM的参数c和g进行迭代寻优，搜索范围都为[0.001，1000]。

4.4 仿真结果与分析

4.4.1 训练结果分析

为了验证算法的优化效果，本文将AWPRPSO与PSO、GA算法对SVM参数进行寻优的结果进行比较。分别使用LMDRT特性增强前后的训练集训练入侵检测模型，在训练的过程中，算法的运行时间和训练精度见表2。

从表2可以看出，在LMDRT变换后，每种算法的准 确精度和训练时间均有了一定程度的改善，且变换后数据的训练精度均高于变换前，说明LMDRT增强了数据的特征，通过了数据质量。且变换后的数据训练时间在同一算法下有了一定的改善，也验证了变换后数据提高数据分类的效率。

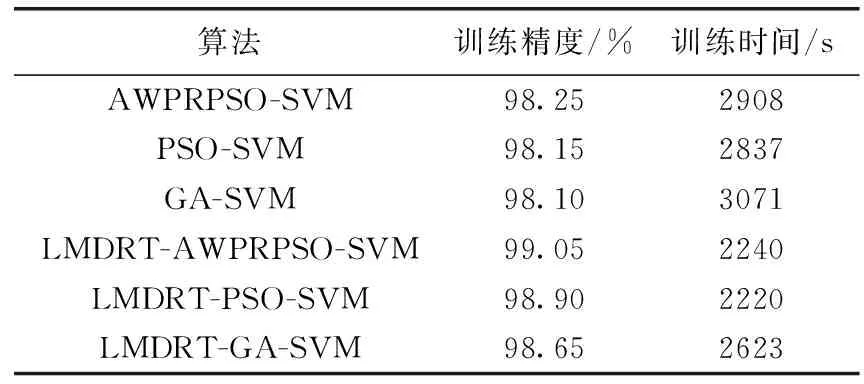
表2 训练时间和训练精度

LMDRT变换后的数据训练集在各算法优化SVM的5折训练精度与迭代次数关系曲线如图3所示。

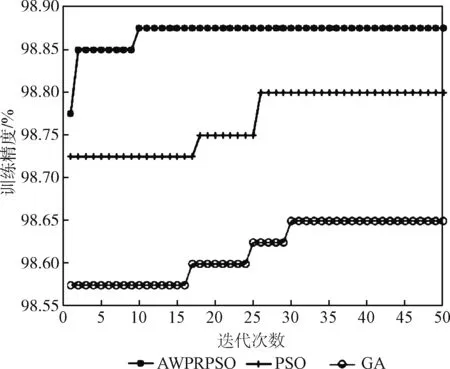
图3 不同算法优化SVM的训练准确率曲线

从表2和图3可以得到，AWPRPSO算法对SVM的寻优精度最高，达到了98.88%，GA算法的精度最低，只有98.65%。算法的收敛速度方面，AWPRPSO的收敛速度最快，第10代左右就收敛到最优；PSO次之，在第26代左右收敛到最优；而GA收敛最慢。综合来说，AWPRPSO在收敛速度与寻优结果上都有着一定优势。

4.4.2 测试结果分析

(1)总体的检测效果分析。根据入侵检测的评价标准。记录变换前后各个算法下使仿真结果用准确率、误报率和漏报率指标来评估模型的分类性能。记录实验的总体结果见表3。

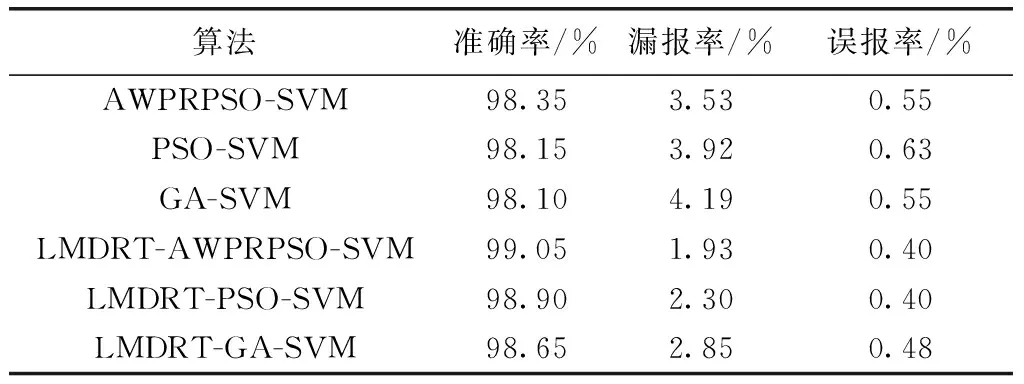
表3 各个入侵检测模型的检测结果

根据表3，LMDRT变换后数据在每种算法下的结果准确率、误报率、漏报率整体优于变换前数据，其中，AWPRPSO-SVM的准确率最高，为99.05%，误报率最低为仅为1.93%，漏报率与PSO-SVM同为最低只有0.4%，整体检测效果相比其它方法有了一定程度的改善。综合可得，基于AWPRPSO-SVM在构建的入侵检测模型具有良好的检测效果，而且对数边际密度比变换后数据可以有效提高入侵检测模型的性能。

(2)各攻击类型数据检测效果分析。MSU工控入侵检测标准数据集包含8种攻击形式(包括正常数据)，图4为变换后数据在各个算法下8种攻击形式的检测准确率曲线。

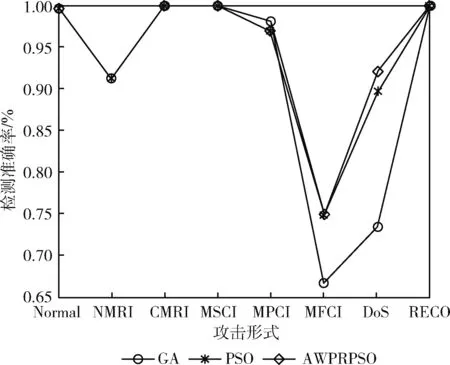
图4 8种攻击形式的检测准确率曲线

从图4可以看出，在检测NMRI、CMRI、MSCI和RECO攻击时各个算法检测效果基本一致；在检测MPCI、MFCI以及Dos攻击时，AWPRPSO和PSO监测效果高于GA，检测MPCI和Dos攻击时AWPRPSO表现明显优于其它算法。

图5是LMDRT-AWPRPSO-SVM模型对测试集进行预测分类的结果和理论分类的结果对比。

图5 LMDRT-AWPRPSO-SVM入侵检测分类结果

从图5中可观察LMDRT-AWPRPSO-SVM分类器测试集数据的整体分布以及误分点的情况。由图可知，该方法在检测NMRI、CMRI、MSCI、MPCI和RECO攻击时效果优异，几乎没有误分的情况；但MFCI和Dos攻击时，由于攻击数据整体偏少，误分的情况较严重。

5 结束语

针对传统工控入侵检测数据转换方法下分类信息利用不充分而导致检测效果不佳，本文采用对数边际密度变换对数据特性进行增强，取得了良好的效果。另外为提高SVM入侵检测模型的准确率，本文将结合自适应权重和粒子重构策略的粒子群优化算法进行SVM的参数c和g进行寻优，使用寻优得到的SVM分类器构建入侵检测模型，并对模型进行实验验证。对比增强前后的数据的实验结果，总结得出：增强后的数据提高SVM入侵检测模型的性能，且AWPRQPSO优化之后的SVM入侵检测模型的总体上性能也优于其它算法优化的SVM模型。LMDRT-AWPRQPSO-SVM在工控入侵检测方面有着良好的表现，对未来相关研究具有一定参考价值。