具有记忆功能的海鸥优化算法求解方程组

许 乐，莫愿斌,2+，卢彦越

(1.广西民族大学 人工智能学院，广西 南宁 530006；2.广西民族大学 广西混杂计算与集成电路设计 分析重点实验室，广西 南宁 530006；3.广西民族大学 化学化工学院，广西 南宁 530006)

0 引 言

目前，求解方程组的智能优化算法有环拓扑混合群体智能算法[1]、粒子群优化算法[2]、正余弦算法[3]、锥模型信赖域算法[4]以及布谷鸟算法[5,6]等，这些算法解决了很多科学、社会、工程等领域的复杂问题。

其中，海鸥优化算法(SOA)[7,8]是Dhiman G博士等提出的一种智能优化算法，通过模拟海鸥的生活习性(迁徙行为和攻击行为)而建立的数学模型，和其它智能优化算法进行比较，SOA算法的基本原理易懂，易于实现，具有全局搜索和局部搜索的能力等特点。但是，SOA算法也存在容易陷入局部最优、过早收敛以及求解精确度低的缺点，因此，许多学者进行了一系列的研究和改进。例如：文献[9]将改进的海鸥优化算法用于PEM燃料电池实验建模，提高了算法的性能。文献[10]将海鸥优化算法应用在四川盆地渝西区块H井区页岩气储层最优化测井解释中。

为解决基本的海鸥优化算法(SOA)存在的缺点，提出一种具有记忆功能的海鸥优化算法(MSOA)。该算法考虑到了海鸥具有记忆功能，即海鸥的前期搜索经验对后期搜索提供了一系列的支持。通过引入记忆功能来提高算法的求解能力和精确度，避免算法陷入局部最优。文中通过引入标准测试函数对MSOA算法进行性能的测试，同时引入了方程组进行仿真实验，通过算法之间的对比表明该算法在解的数量和质量上都具有优势，进一步验证了MSOA算法的寻优能力。

1 问题描述

(1)线性方程组是各个方程关于未知量均为一次的方程组，其一般形式如下

(1)

方程组可以转化Ax=b，进一步转化：Ax-b=0，令f(x)=Ax-b，则构造目标函数如下

F(x)=f12(x)+f22(x)+…+fn2(x)

(2)

(2)设非线性方程组[11,12]如下

(3)

所以，为了计算出适应度值，把线性方程组和非线性方程组的求解问题统一转换为目标函数的最小值思想，即目标函数就是适应度函数。目标函数统一如下所示

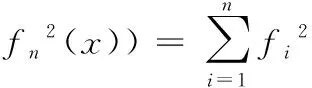
(4)

2 改进的海鸥优化算法

2.1 引入记忆功能

海鸥优化算法的介绍以及相关定理请参考引言里面的文献，文中MSOA算法是在SOA算法海鸥群体进行攻击行为基础上改进的，引入两个随机因子以及两个学习因子；同时在种群更新中，加入了海鸥种群的最佳位置和个体的历史最优值。一方面，MSOA算法使得海鸥向个体历史最优位置的学习；另一方面，它又增强了向群体最佳位置的学习，从而避免了种群陷入局部最优解区域，增强了种群的寻优性能。记忆功能的公式如下所示

Pm(t)=ds(t)×x×y×z+Pbs(t)+(Pg(t)-Ps(t))×r1×w1+(Pbs(t)-Ps(t))×r2×w2

(5)

式中：随机因子r1和r2设置为0和1之间的随机数，从而增强海鸥飞行过程中的随机性，学习因子w1、w2的值设置为0.9，从而保证算法能够更好收敛，增强了海鸥向个体学习以及群体学习的能力，Pg(t)表示海鸥个体的历史最优位置，Pm(t)为记忆个体，Ps(t)为上一代个体。

为了增强算法的求解能力，需要将迭代出来的海鸥位置，即记忆个体与上一代个体位置的适应度进行比较，选出最优的位置。判断如下所示：

if 记忆个体的适应度值>上一代个体的适应度

上一代个体位置替换记忆个体位置

else

记忆个体的位置保持不变

MSOA算法不但更新当前群体的全局最优值，而且更新了每个海鸥个体的历史最优信息。这样不仅能够使海鸥个体跳出局部极值进入解空间的新区域继续进行搜索最优解，也还能够提高算法的收敛精度和收敛速度，避免陷入局部最优。

2.2 MSOA算法的求解步骤

具有记忆功能的海鸥优化算法的求解过程分为初始化过程、适应度计算过程、循环迭代过程、筛选过程、更新适应度值和位置过程、输出结果过程6个过程。具有记忆功能的海鸥优化算法(MSOA)的求解步骤如下所述：

步骤1种群初始化。设置种群大小popsize，最大迭代次数maxiter，线性频率fc，螺旋形状的参数u、v等；

步骤2计算当前海鸥种群每个个体的适应度值，计算出当前海鸥种群的全局最优位置和设置个体最优位置；

步骤3迭代寻优，更新海鸥的位置；

步骤4计算出海鸥避免碰撞后的新位置；

步骤5计算出海鸥的最佳位置方向；

步骤6计算海鸥靠近最佳位置；

步骤7引入具有记忆功能式(5)结合攻击行为的公式计算出海鸥的新位置，从而得到新的一代海鸥个体；

步骤8比较记忆个体和上一代个体的适应度值，把最好的个体保存下来；

步骤9更新海鸥的位置和适应度值，个体更新和全体更新；

步骤10是否满足条件，若满足，结束循环，否则，继续迭代寻优；

步骤11输出海鸥的最佳位置和适应度值、输出迭代过程；

步骤12结束程序。

3 实验结果与分析

为了测试MSOA算法的寻优能力和精确度，首先使用10个标准测试函数进行测试，测试算法的寻优能力；最后，将MSOA算法运用在求方程组的解，其中，方程组包括5个线性方程组和10个非线性方程组。实验中使用的仿真软件是MATLAB R2017a，操作系统是windows10，64位，处理器Intel(R) Core(TM) i5-8300H CPU @ 2.30 GHz 2.30 GHz。

3.1 标准测试函数的测试

算法的参数设置：最大迭代次数都为200，SOA算法的种群大小为200，线性频率fc为2，两个螺旋参数u和v的大小都为1；PSO算法的种群大小为200，学习因子为2，惯性因子等于0.8；MSOA算法的种群大小为80，频率fc为2，两个螺旋参数u、v的大小分别为0.001、0.9。在本次实验中，每个标准测试函数的维度都设置为30，每个函数都分别独立运行10次，分别统计出SOA算法、PSO算法以及MSOA算法的平均值、最优值以及最差值。其中，表1说明了标准测试函数相关参数的设置，表2给出了3种算法的不同函数实验结果；为了体现算法的寻优效果，图1～图10给出了每个函数对应的迭代曲线图。

表1 标准测试函数的相关参数

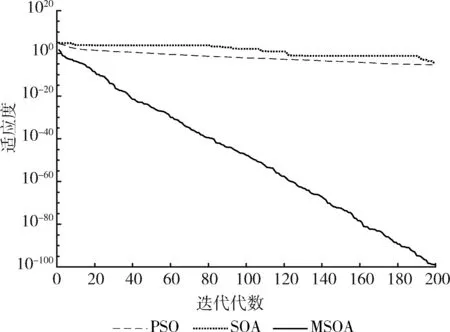
图1 函数f1的迭代曲线

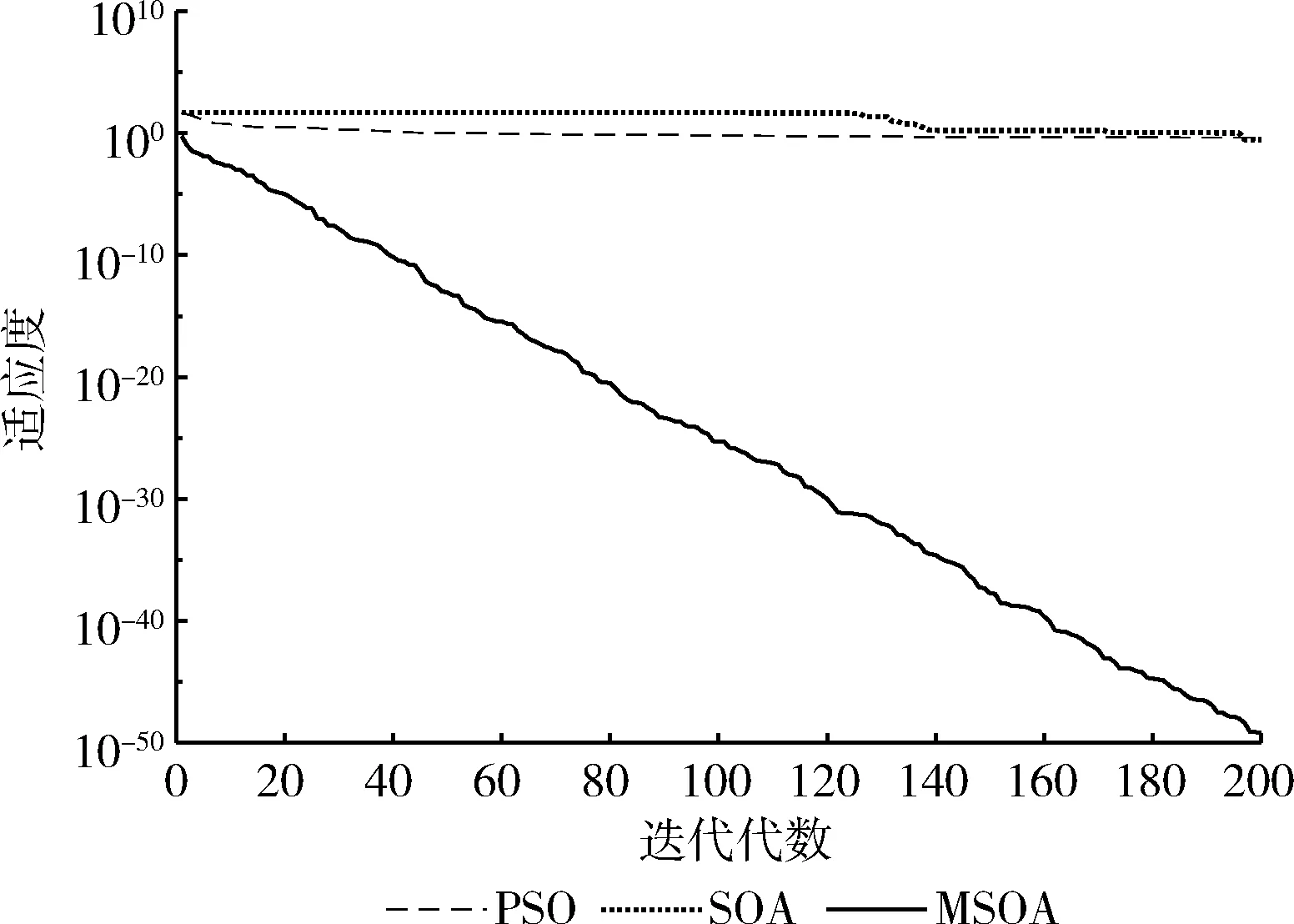
图2 函数f2的迭代曲线

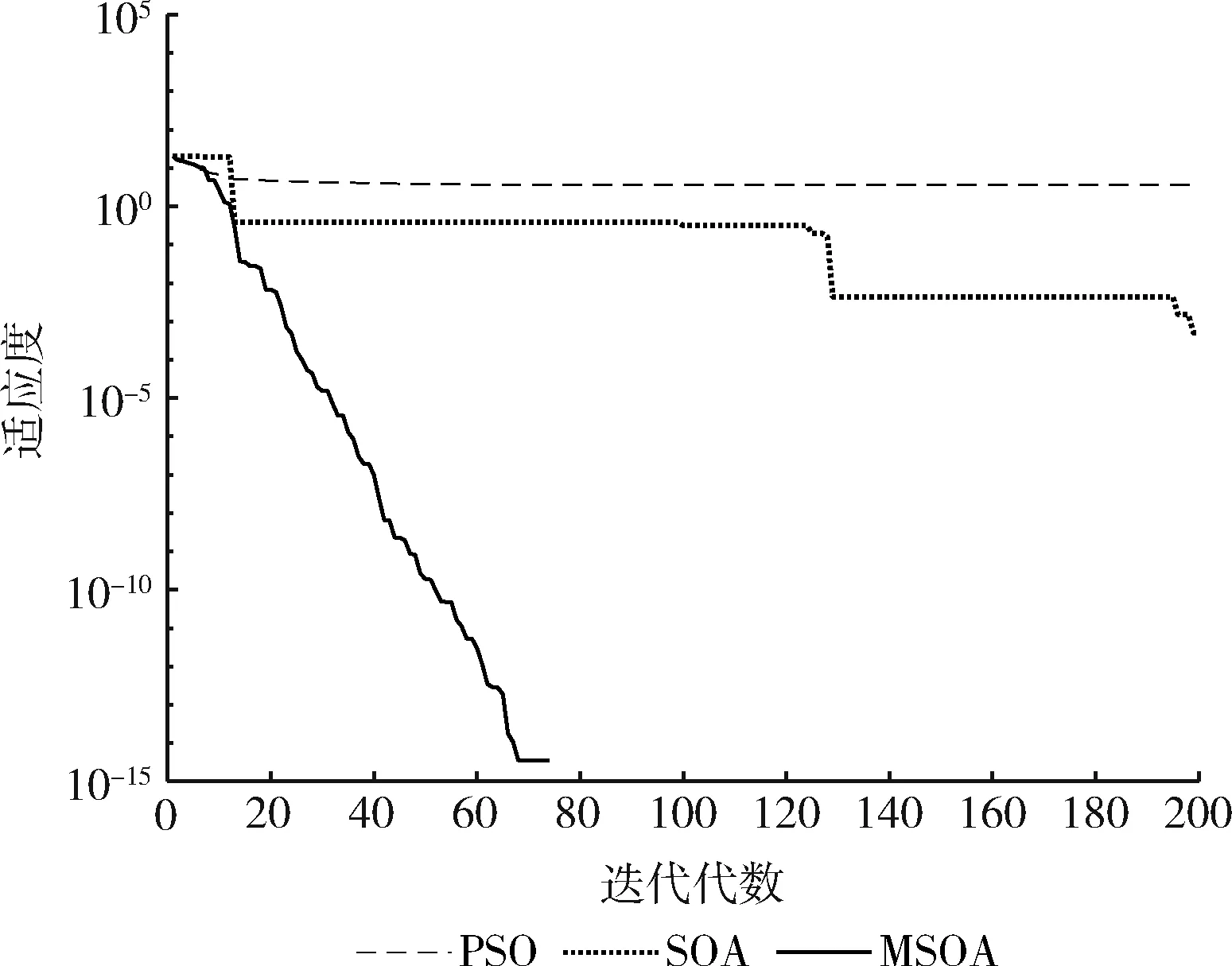
图3 函数f3的迭代曲线

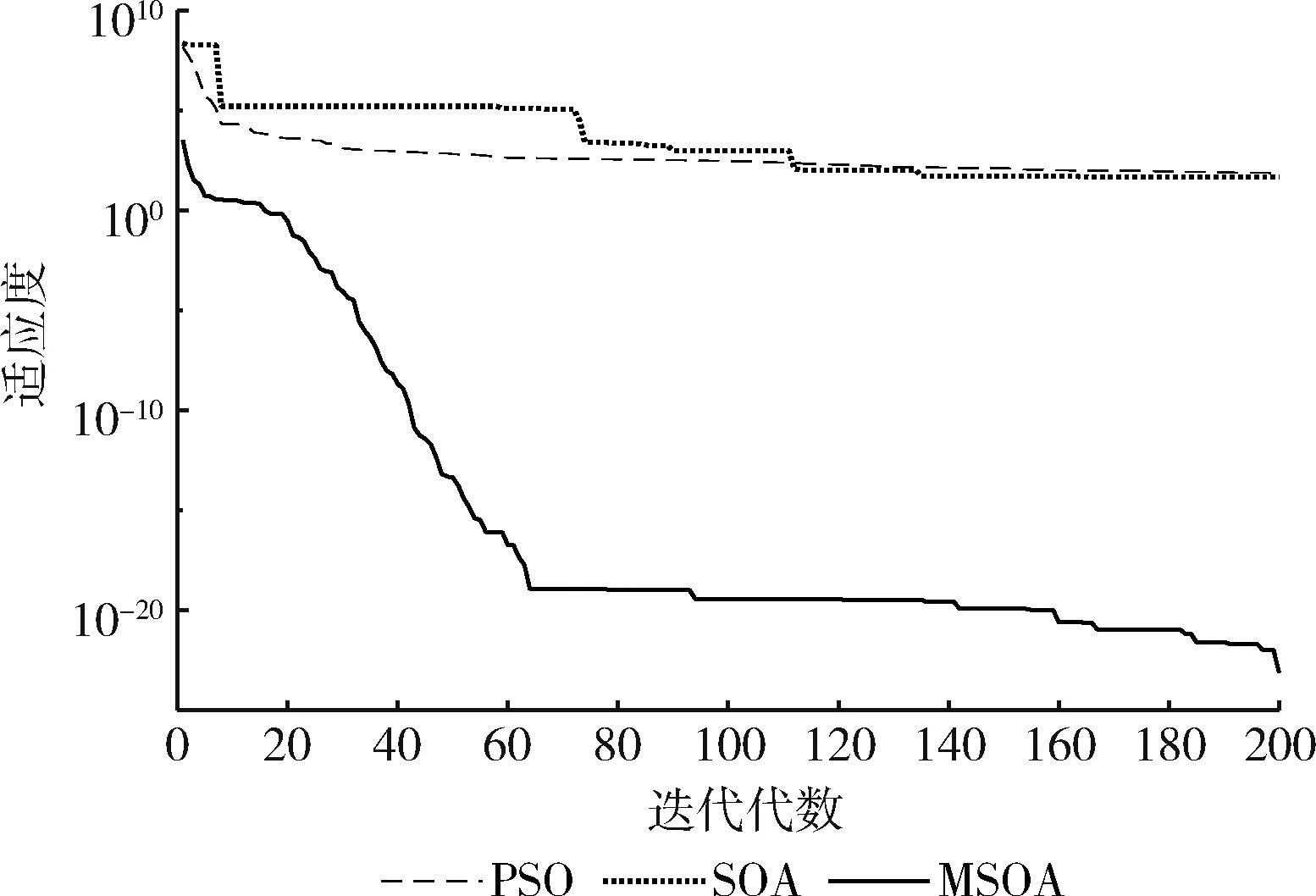
图4 函数f4的迭代曲线

表2 SOA、PSO、MSOA算法的实验结果

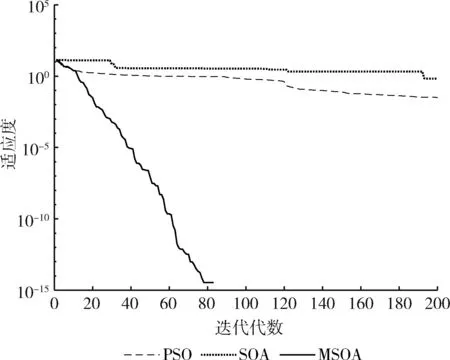
图5 函数f5的迭代曲线

图6 函数f6的迭代曲线

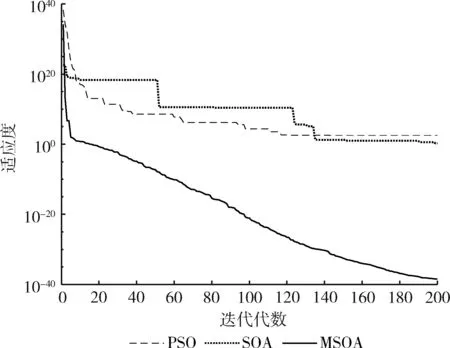
图7 函数f7的迭代曲线

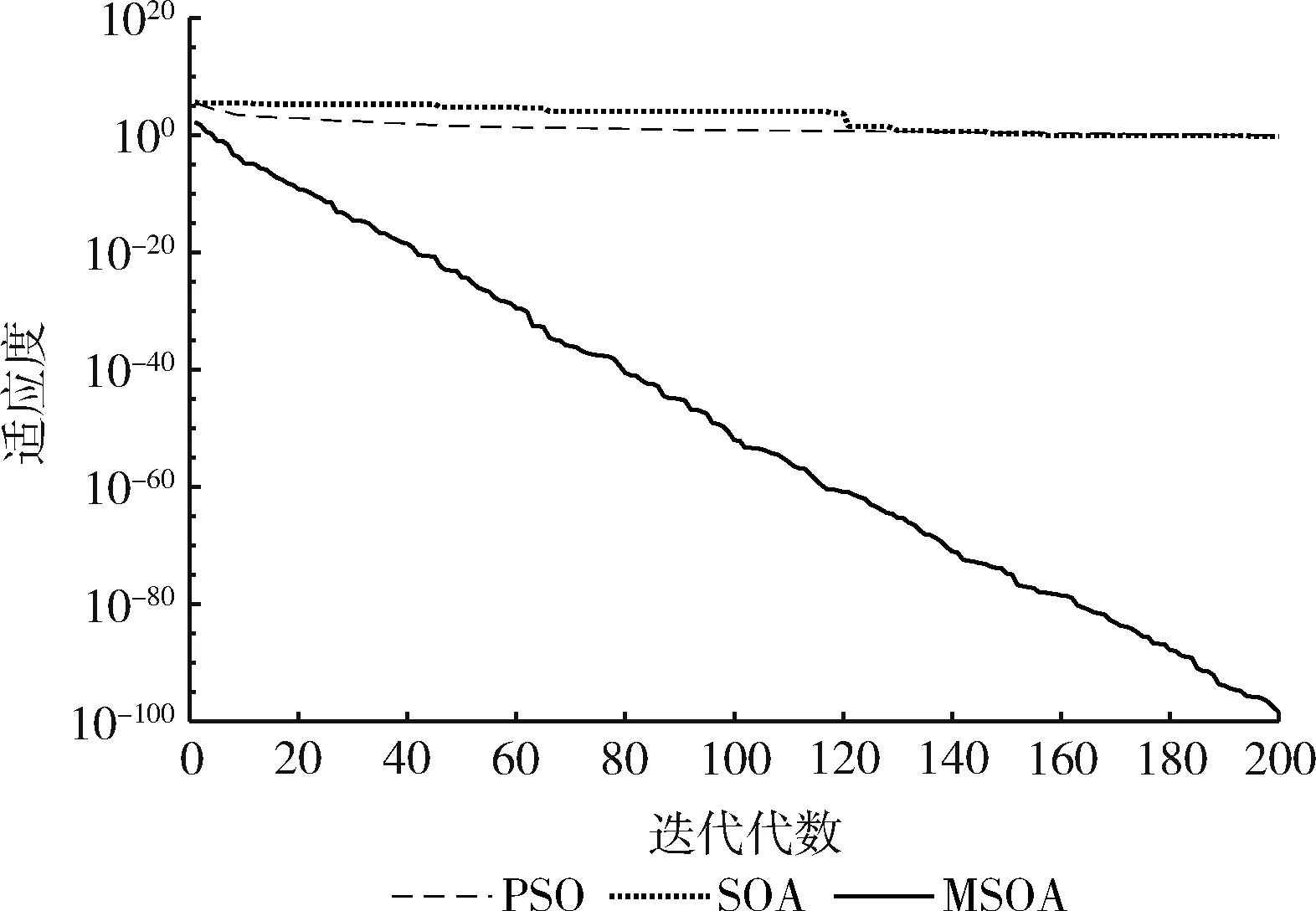
图8 函数f8的迭代曲线

图9 函数f9的迭代曲线

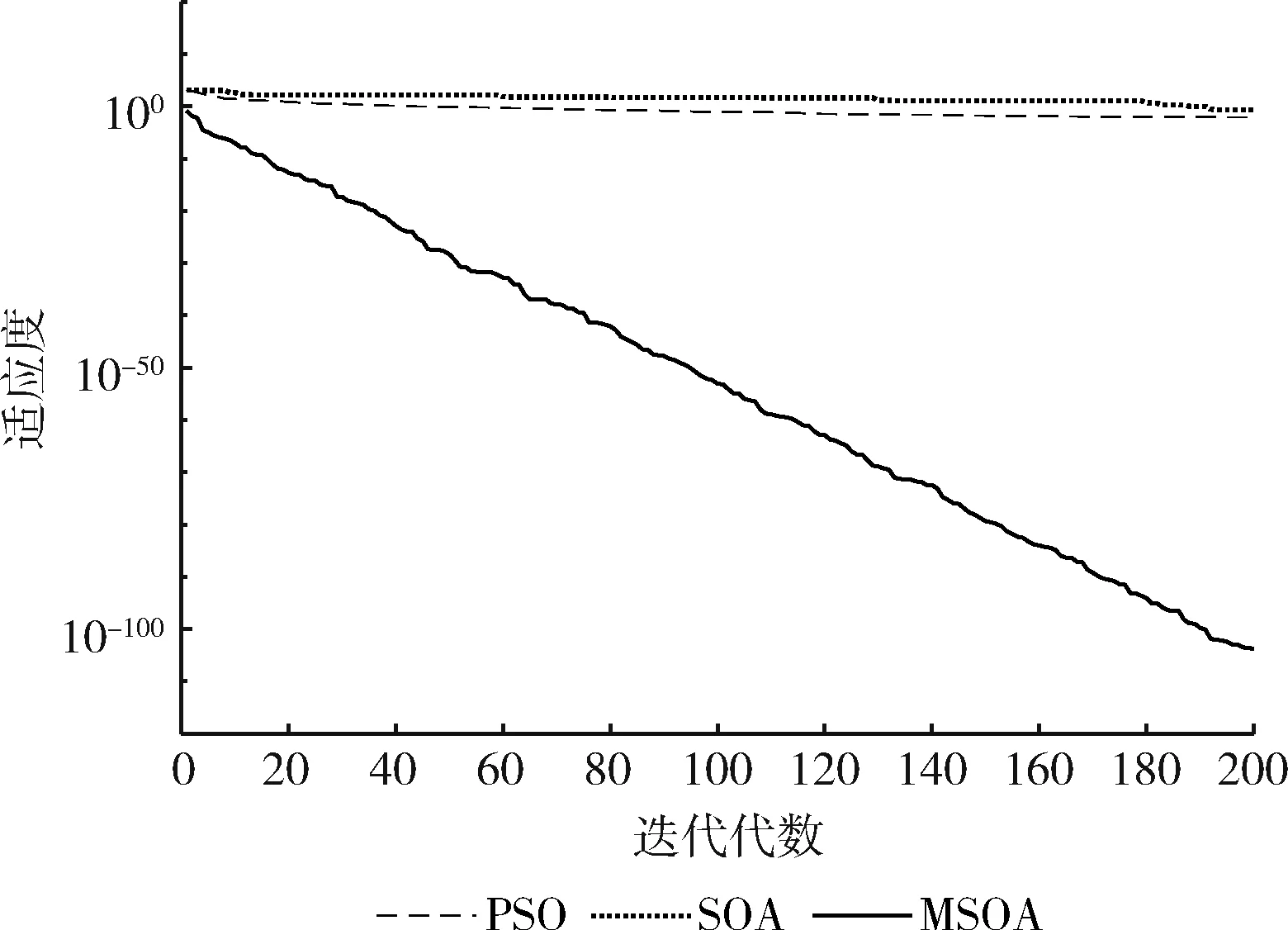
图10 函数f10的迭代曲线

实验结果分析：从表2可以看出，通过MSOA、SOA、PSO算法进行对比，MSOA算法具有更好的寻优能力，其值更接近于理论值。对于单峰函数f1，MSOA的平均求解精度更高，比PSO高了95个数量级，SOA的平均值没有找到最优值。对于函数f2，MSOA的平均求解精度比SOA、PSO高了49个数量级。对于函数f3，PSO算法没有找到理想值，SOA的求解精度比PSO高，MSOA算法的值为0，与理论值一样，说明MSOA求解能力以及精度比PSO、SOA好。对于函数f4，SOA与PSO在平均值上都没有找到理想最优解，MSOA的求解效果最好，平均求解精度为e-23。对于函数f5，PSO的平均求解精度比SOA高了1个数量级，但是MSOA值为0与理想值完全一样，求解精度更高。对于函数f6，SOA与PSO的求解精度一样，能够找到较为理想的解，但是MSOA的求解精度比两者高了24个数量级。对于函数f7，SOA没有搜索到理想的值，MSOA的平均求解精度比PSO算法高了24个数量级。对于函数f8，SOA与PSO都没有在最大的迭代次数内找到最优值，MSOA算法的平均求解精度最高。对于函数f9、f10，SOA与PSO都能找到合理的解，但是通过最优值、最差值以及平均值进行比较，MSOA算法的效果更好。从图1～图10的迭代曲线可以看出，MSOA算法能够避免陷入局部最优解，使得算法求解精度较高，搜索解的能力较好。

3.2 线性方程组的测试

为了测试该算法求解线性方程组的性能，选取了5组线性方程组[13]进行了测试，每个方程独立运行10次，结果取平均值，实验结果见表3。实验参数的设置：PSO算法的最大迭代次数为200，种群大小为200，学习因子为2，惯性因子等于0.8；人工鱼群算法(AFSA)的种群大小为80，最大迭代系数为200，感知距离visual=1，移动最大步长step=0.01，最多试探次数try_number=100，拥挤度因子delta=0.618；斑鬣狗优化算法(SHO)[14]的种群大小为30，迭代次数为100；MSOA算法的种群大小为200，最大迭代次数为100。线性方程组如下所示

其中，方程组(1)的理论值为(1,3,6)；方程组(2)的理论值为(0.3333,0.3333,0)；方程组(3)的理想值为(12,27,6,-13)；方程组(4)的理论值为(1,2,3,4,5)；方程组(5)的理论值为(1,2.5,3,6.5,7)。

实验结果分析：从表3可以看出，对于方程组(1)，利用传统方法(牛顿法)能够求出理想值，PSO、AFSA以及SHO算法的值接近理论值，SOA的值与理论值有一定的差距，通过比较，MSOA的求解精度更好；对于方程组(2)，5种方法都能找到理论值、精确度较高，但是SOA存在求解精度偏低；对于方程组(3)，AFSA、SOA在最大迭代次数内没有找到理想解，MSOA的平均精度比PSO、SHO高；对于方程组(4)，传统方法、PSO、AFSA以及SHO的解接近理论值，但MSOA的效果更好；对于方程组(5)，牛顿法、AFSA、SOA算法偏离理想值，PSO和SHO的值接近理想值，但是MSOA更具有优势，说明传统方法已经不适合大型计算。总的来说，MSOA算法的寻优能力和求解精度都比其它算法的效果好。

3.3 非线性方程组的测试

为了测试MSOA算法在求非线性方程组的性能，文中引入了文献[15,16]中的非线性方程组进行了仿真实验，MSOA、SOA、PSO、SHO的种群大小为500，最大迭代次数为1000，其它参数和线性方程组测试一致。其中方程组(1)～方程组(6)分别运行10次取平均值，方程组(7)～方程组(10)分别运行50次取平均值。实验结果见表4～表6，图11给出了方程组(10)的进化曲线，非线性方程组如下

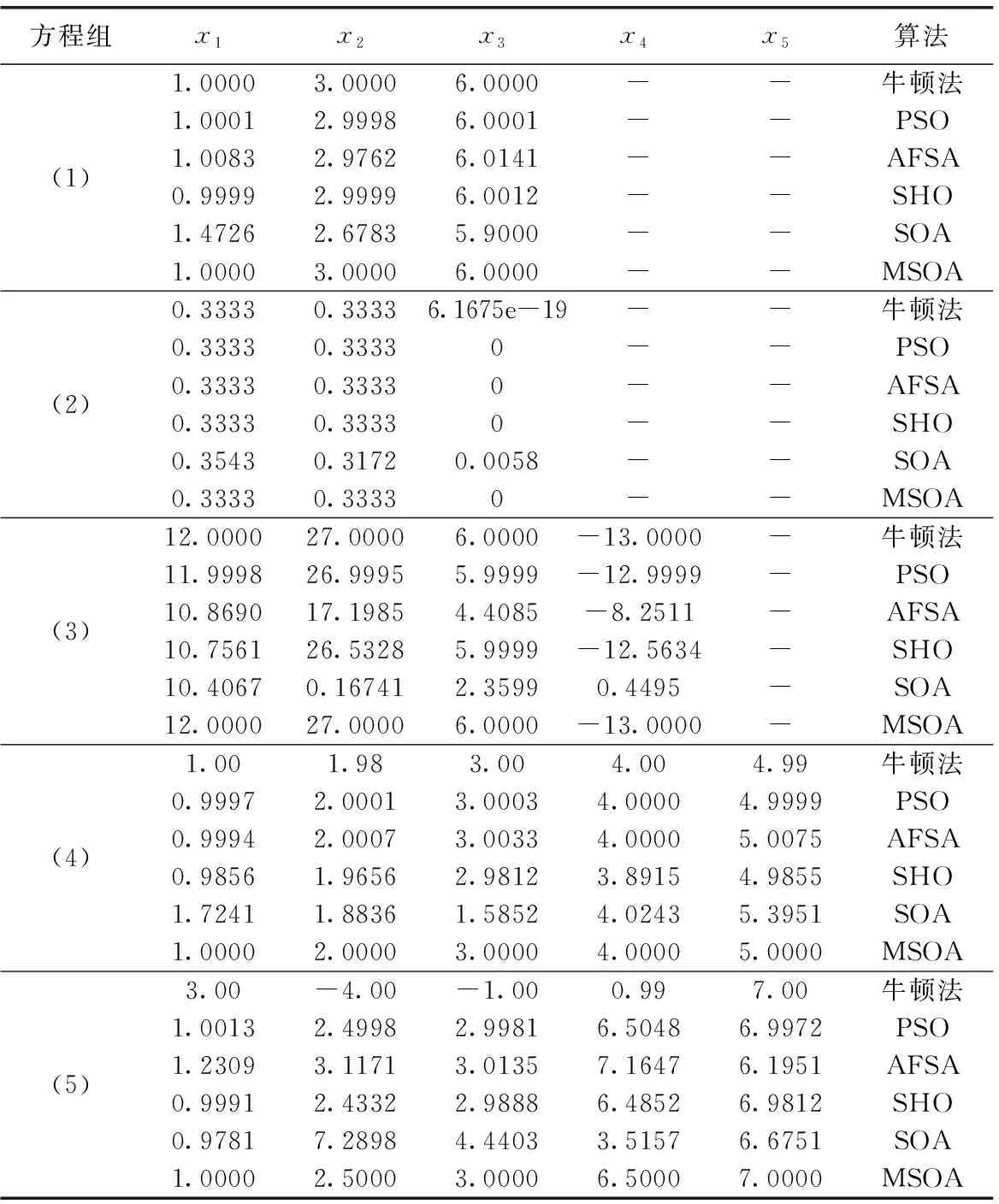
表3 线性方程组的实验结果

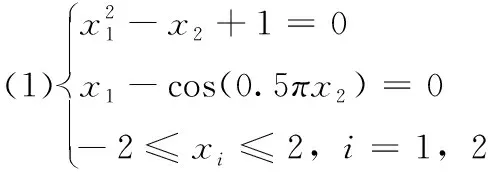
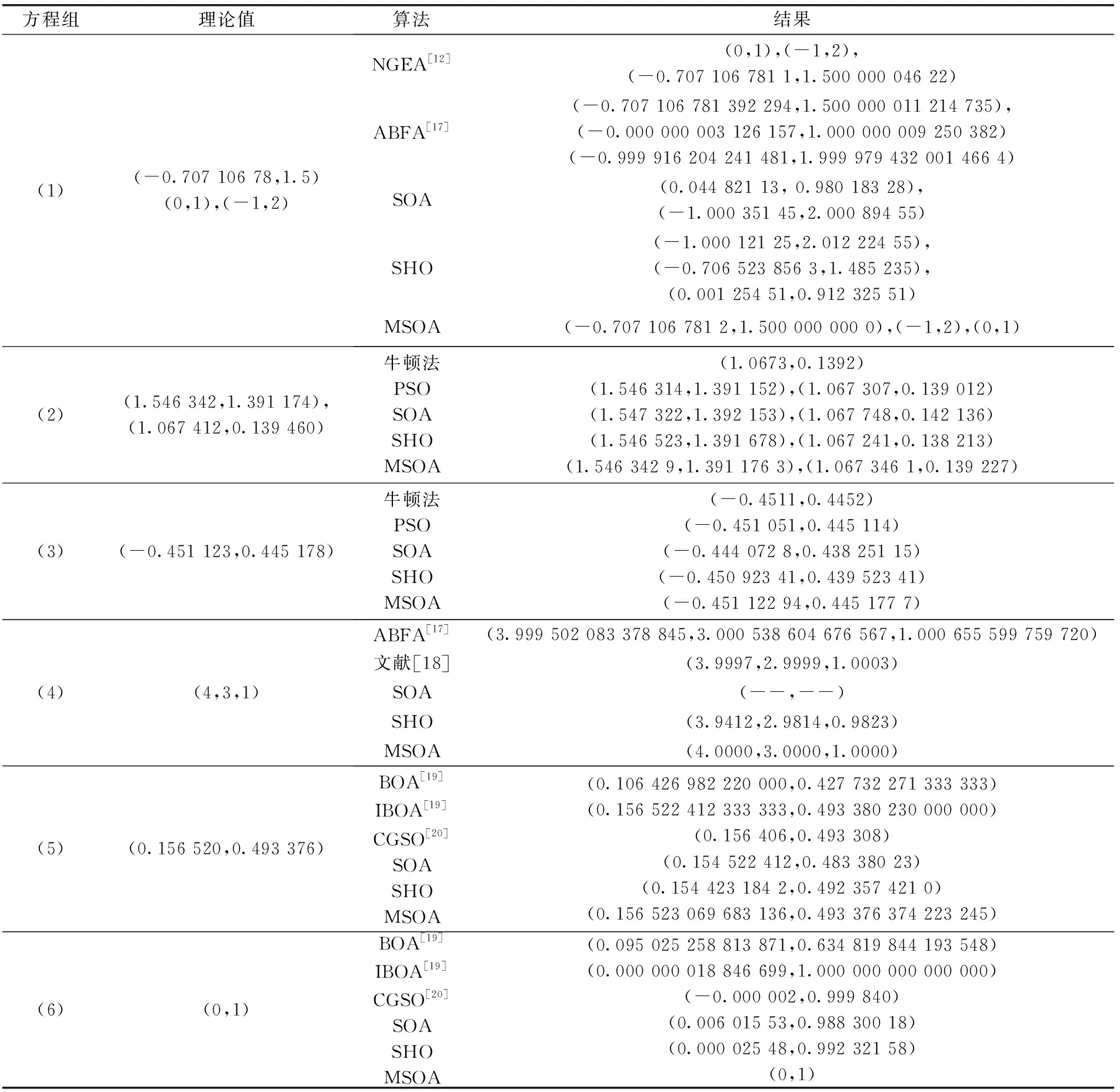
表4 非线性方程组(1)～方程组(6)的实验结果

实验结果分析：从表4可知，对于方程组(1)，文献[12]和文献[17]能够找出方程组的全部解且其值接近于理论值，SOA算法只能找出两个解且求解精度不高，SHO算法找出了3个解，但是求解精度不高，而MSOA算法更具有优势；对于方程组(2)、方程组(3)，MSOA算法的求解精度都要高于其它算法；对于方程组(4)，ABFA算法的值接近于理论值，文献[18]的求解精度较高，SOA算法没有找到值，SHO算法的求解精度一般，但是MSOA的求解精度较高一点；对于方程组(5)，BOA算法没有找到较好的解，而IBOA算法的求解能力比BOA算法要高，CGSO算法的求解精度较好，SOA和SHO算法与理论值有一定的差距，而MSOA算法在求解精度更好；对于方程组(6)，BOA和IBOA算法相比，IBOA算法更具有优势，CGSO、SOA、SHO算法的值接近于理论值，而MSOA算法的精确值为0和1，求解精度优于参考文献中的算法。所以，MSOA算法具有较好的求解能力。

测试方程组(7)～方程(9)，其中，方程组(7)有4个近似解，分别为(0.8165,1.547)，(-0.8165,-1.547)，(-0.8165,1.547)，(0.8165,-1.547)。方程组(8)也有4个近似解，解分别为(-1.563 53,0.277 63)，(-0.789 71,1.088 30)，(1.563 53,0.277 63)，(0.789 71,1.088 30)。方程组(9)有10个近似解，分别为(-1.810 89,-0.349 09)，(-1.810 89,0.349 09)，(-1.502 22,-0.409 08)，(-1.502 22,0.409 08)，(-1.791 30,0.301 93)，(-1.791 30,-0.301 93)，(-0.947 27,0.785 02)，(-0.947 27,-0.785 02)，(-0.213 06,1.256 85)，(-0.213 06,-1.256 85)。

实验结果分析：从表5可知，对于方程组(7)、方程组(8)，MSOA算法能够找出方程的全部解，通过与提供的近似解相比，发现MSOA算法的解接近于近似解，精确度较高，寻优的能力较好，MMODE算法[16]也能找出4个最优解，搜索到的全部解还没有完全接近于理论解，但是该算法的最大迭代次数为50 000，运行时间较长，所以在时间方面MSOA算法更具有优势；对于方程组(9)，MMODE算法[16]找出了方程组的全部解，且搜索到的解与真实值比较接近，IBA算法[21]也能找出方程组的全部解且求解的成功率达到了100%，而MSOA算法能够找出10个最优解，接近于理论解，通过MMODE、IBA、MSOA算法的结果进行对比，改进算法具有一定的优势。

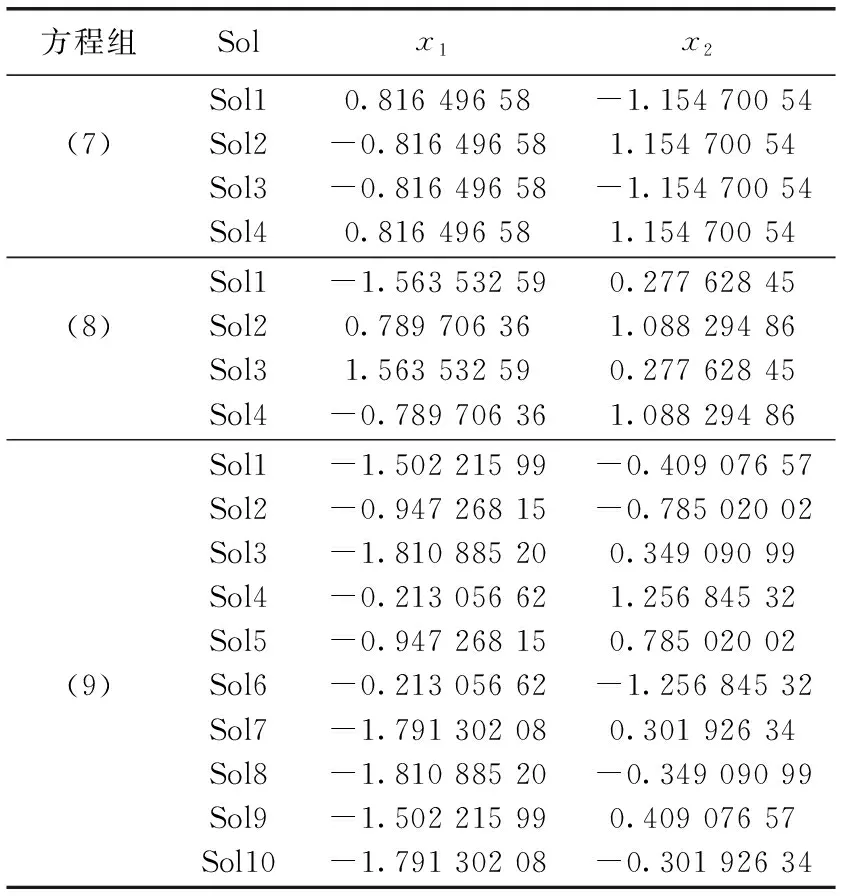
表5 非线性方程组(7)～方程组(9)的实验结果

测试方程组(10)，其中，对于方程组(10)，方程组有16个解，分别如下所示：(0.1644,-0.9864,-0.9471,-0.321,-0.9982,-0.0594,0.411,0.9116)、(0.1644,-0.9864,-0.9471,-0.321,-0.9982,0.0594,0.411,-0.9116)、(0.1644,-0.9864,-0.9471,-0.321,0.9982,-0.0594,0.411,0.9116)、(0.1644,-0.9864,-0.9471,-0.321,0.9982,0.0594,0.411,-0.9116)、(0.1644,-0.9864,0.7185,-0.6956,-0.998,-0.0638,-0.5278,0.8494)、(0.1644,-0.9864,0.7185,-0.6956,-0.998,0.0638,-0.5278,-0.8494)、(0.1644,-0.9864,0.7185,-0.6956,0.998,-0.0638,-0.5278,0.8494)、(0.1644,-0.9864,0.7185,-0.6956,0.998,0.0638,-0.5278,-0.8494)、(0.6716,0.741,-0.6516,-0.7586,-0.9625,-0.2711,-0.4376,0.8992)、(0.6716,0.741,-0.6516,-0.7586,-0.9625,0.2711,-0.4376,-0.8992)、(0.6716,0.741,-0.6516,-0.7586,0.9625,-0.2711,-0.4376,0.8992)、(0.6716,0.741,-0.6516,-0.7586,0.9625,0.2711,-0.4376,-0.8992)、(0.6716,0.741,0.9519,-0.3064,-0.9638,-0.2666,0.4046,0.9145)、(0.6716,0.741,0.9519,-0.3064,-0.9638,0.2666,0.4046,-0.9145)、(0.6716,0.741,0.9519,-0.3064,0.9638,0.2666,0.4046,-0.9145)、(0.6716,0.741,0.9519,-0.3064,0.9638,-0.2666,0.4046,0.9145)。

表6 非线性方程组(10)的实验结果

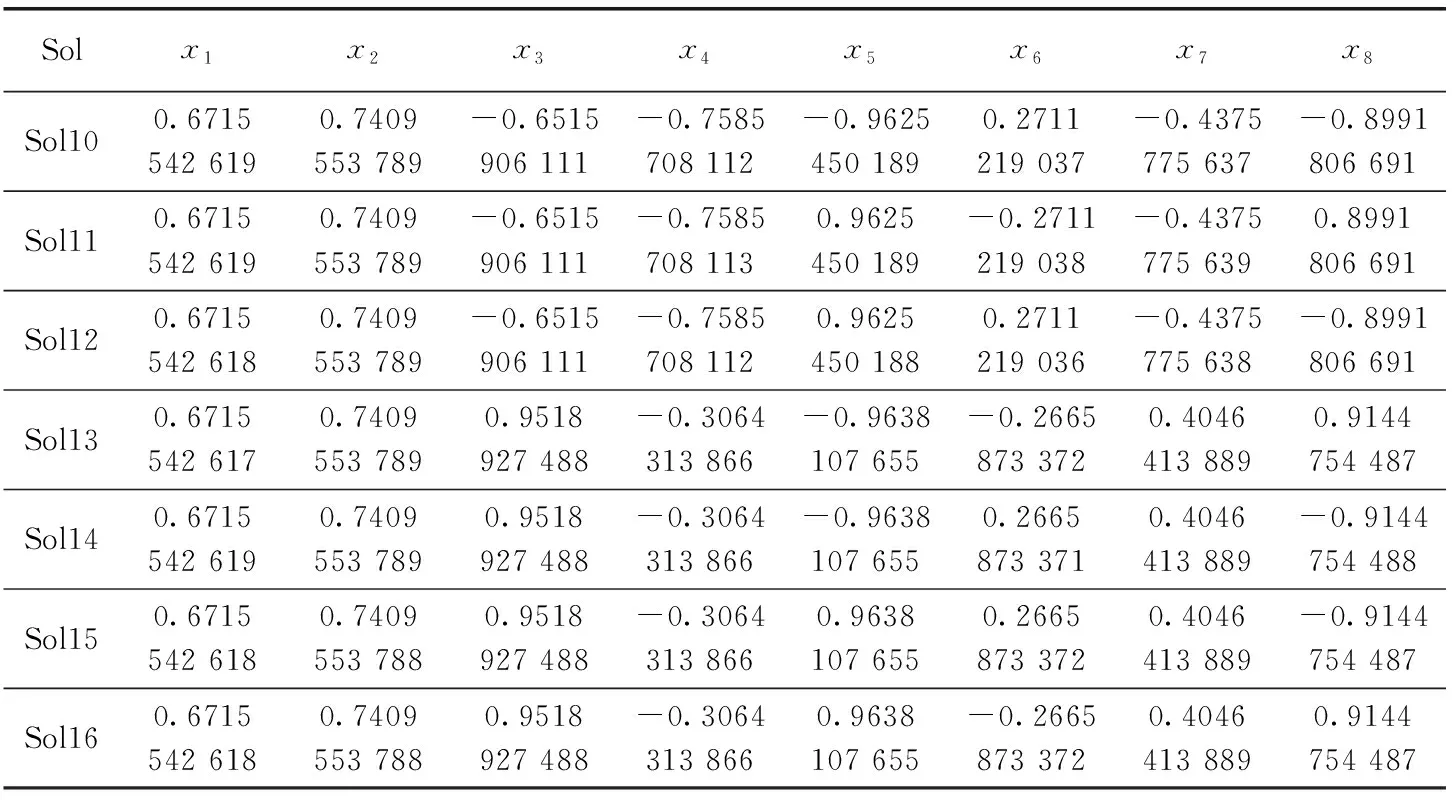
续(表6)

实验结果分析：从表6可知，对于含有16个解的方程组(10)，MSOA算法找出了方程组的全部解且求解精度较高，而MMODE算法[16]求解该问题时，16个解还不能很好地搜索到，IBA算法[21]在最大迭代次数为5000时，搜索到了15个近似解且成功率为93.75%。从方程组的进化曲线图可以看出，MSOA算法在求解该问题时能够在较短的时间内收敛。通过比较，进一步说明改进算法的寻优能力较好。

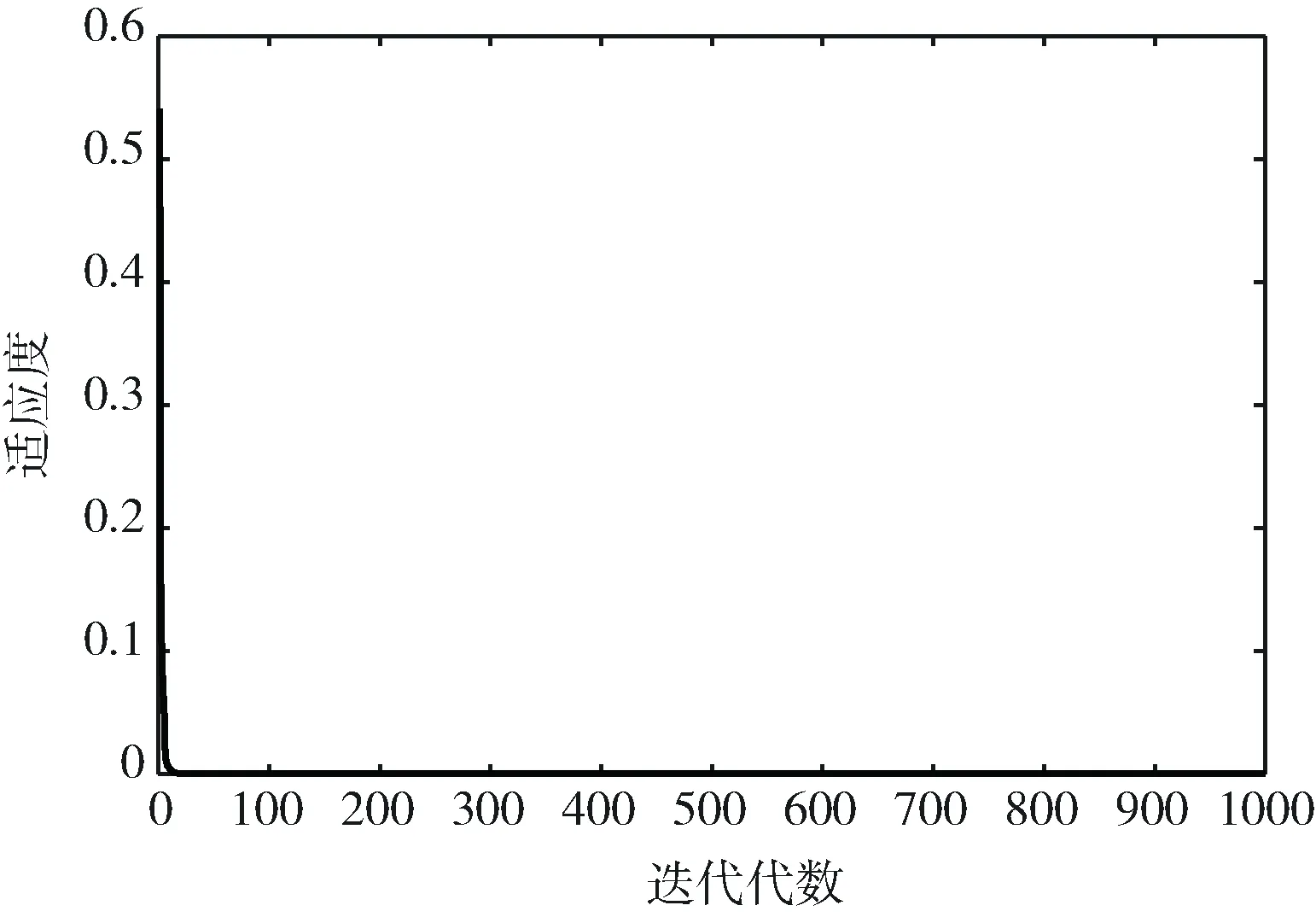
图11 方程组(10)的进化曲线

4 结束语

分析了基本的海鸥优化算法(SOA)存在容易陷入局部最优的问题，提出了一种具有记忆功能的海鸥优化算法(MSOA)。在算法测试方面，首先引入了10个标准测试函数进行测试，通过PSO算法以及SOA算法的对比，结果说明MSOA算法具有良好的寻优能力；其次，MSOA算法对5个线性方程组进行求解，通过与传统方法、其它智能算法进行比较，MSOA算法的平均求解精度、最优值等都要优于其它方法；最后，引入了10个非线性方程组进行测试，MSOA算法分别与文献中的方法以及其它新算法进行仿真对比，结果表明该算法在求解的数量以及精确度上都具有一定的优势，进一步说明MSOA算法的寻优能力较好。