罚处共享最近邻密度峰聚类算法

高润峰，苏一丹，覃 华

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

密度峰聚类算法(density peak clustering，DPC)，具有对初始点不敏感、能对各种形状进行聚类等优点[1]。但该算法也存在一些不足，例如：需要手动选择聚类中心点，主观性较大，自动化程度差；当簇的密度差异较大的时候，密度较小簇的中心点不容易被发现导致聚类结果不准确。针对这些问题，国内外学者进行了研究。Xie等用K近邻计算样本点的密度，并采用模糊加权K近邻来分配样本[2]；Liu等提出用高斯核确定阈值来自动选择聚类中心[3]；Liu Rui等通过共享最近邻和两次分配策略优化非簇中心点的分配[4]；王洋等利用基尼系数自动识别聚类中心[5]；Sun等提出一种基于数据分布和线性判断的自动选择簇中心方法[6]；贾露等采用物理学中的万有引力来优化密度峰聚类[7]；Zhao等将数据空间划分为圆形网格，通过网格相似度来实现密度峰聚类[8]；Cheng等用密度核来避免噪声[9]。

上述改进的DPC算法中，共享最近邻密度峰算法(shared nearest neighbor density peak clustering，SNN-DPC)的聚类效果较好[4]，但仍存在不能自动化选簇中心和容易忽略密度较小的簇等问题，针对这些问题，提出一种罚处共享最近邻密度峰聚类算法(penalty shared nearest neighbor density peak clustering，PSNN-DPC)，主要思路是：首先找出罚处点，使用共享最近邻和罚处系数计算样本点的密度，然后再根据改进的样本密度确定与更高密度点的距离计算γ，根据迭代阈值方法γ进行迭代以选出聚类中心，接着采用二次分配策略将簇的非中心点分配到对应的簇中。通过在各种数据集上的实验，验证所提算法是可行的。

1 共享最近邻密度峰聚类算法

共享最近邻的定义为：对数据集X中的任意一点i和j，点i的K近邻集合为Г(i)，点j的K近邻集合为Г(j)，那么点i和点j的共享最近邻定义为

SNN (i,j) = Γ (i)∩Γ (j)

(1)

SNN相似度(SIM)定义为：对数据集X中的任意一点i和j，有

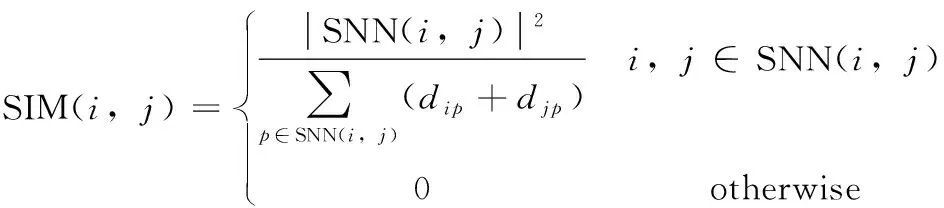
(2)

式中：dip与djp分别是点i和j到它们的共享最近邻集合中一点p的欧氏距离。

SNN局部密度是通过将与点i附近k个相似度最大的点L(i)={x1,x2,x3,…,xk}的SNN相似度(SIM)进行相加，即

(3)

点i为数据集X中的任意一点，其与密度更大最近点j的距离，定义为点i距最近更大密度点的距离(相对距离)即

(4)

特殊的，如果该点是局部密度最大点，点i距最近更大密度点的距离(相对距离)定义为

(5)

点i为数据集X中的任意一点，其决策值为

γi=ρi*δi

(6)

本文采用了罚处思想来改进算法，后文给出密度ρ的新定义。

2 罚处思想与迭代阈值法

2.1 罚处思想

由于SNN-DPC算法的特点：一般来说，SNN局部密度都较大，使得密度在决策值中所占权重较大，会忽略低密度簇的中心点，该算法给出的解决方案是针对特殊数据集采用非常规方法选点，即选择δ较大的点而忽略常规方法中选择γ较大点，但此方法不具备普适性，也无法实现自动化，对此本文提出了一种罚处思想来罚处高密度簇中的非密度中心，改进密度分布不均时的聚类效果，罚处思想主要有两点：第一点是对罚处区域的定义，第二点是对罚处点的定义。

罚处区域：当某一区域点都具有较大的SNN局部密度ρold，如果该数据集中有其它低密度簇的中心点存在，那么传统的密度峰聚类算法会忽略低密度簇的中心点的存在，从而造成忽略低密度簇。为降低低密度区域中，中心点被其附近其它簇高密度点影响，需要对这些高密度中的点的密度进行罚处，这些高密度点所处的区域我们称为罚处区域。

罚处点(penalty point，PP)：当发现其附近k个点的SNN传统局部密度ρold都较高，可以认为其在罚处区域，把在罚处区域的点称为罚处点(penalty point，PP)。将罚处点的k个相似度最大的点分为两类，一类是离该点较近的n个Pi={x1,x2,x3,…,xn}，另一类是离该点较远的z个Qi={x1,x2,x3,…,xz}。根据聚类中心的特点：聚类中心附近的点较密集，所以对该点较近的点贡献的SNN局部密度值不作罚处，但对该点较远的点贡献的SNN局部密度值作罚处，这样对高密度簇中真正的聚类中心影响不大，且可以有效地降低高密度簇中非聚类中心的密度值。由此，我们将SNN新的局部密度定义为

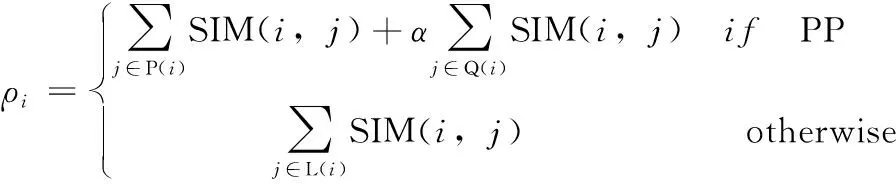
(7)

式中：α为罚处系数，该系数的作用是对惩处点中距离该点较远的z个点贡献的SNN局部密度进行罚处。在传统SNN局部密度中，对SNN局部密度都采用一个度量标准，所以在高密度簇中，每一点的传统SNN局部密度都较高；而在低密度簇中，每一点的传统SNN局部密度都较低，导致会遗漏在密度较小簇中的聚类中心。我们引用罚处系数α后，新的SNN局部密度削弱了高密度簇中的非聚类中心的SNN局部密度值，使得低密度簇中的聚类中心显现出来，从而减少低密度簇中心点被忽视的机率，使得聚类结果更加准确。

距离远近的判断标准：对于数据集X中任意一点i，计算其距离最远的第k个邻居的欧氏距离Ei，若距离小于等于1/2Ei则认为其距离较近，否则认为其距离较远。

2.2 迭代阈值法

迭代阈值法[10]是图像分割中广泛使用的方法，由于图像前景和背景值的差别较大，使用迭代阈值法可以将前景和背景区分开来，利用这一特点，我们将该方法移植到数据集分割上，把一个数据集分割成两个互相之间差别很大的数据集。由于密度峰算法聚类中心的γ的值都远远大于非中心的γ值，非常符合迭代阈值法适用的条件，所以迭代阈值法很适合用于选择密度峰聚类中心。本文用迭代阈值法选出簇中心的子算法如下：

输入：数据集W={μ1,μ2,μ3,…,μn}

输出：阈值T，数据集M和数据集I

步骤1计算数据集W中n个数据的平均值，记为m0，且T=m0；

步骤2将数据集W分为大于等于T和小于等于T两组数据集，分别为M={σ1,σ2,σ3…,σn1}和I={θ1,θ2,θ3…,θn2}；

步骤3令T0=T，对数据集M和数据集I进行求平均值分别为m1，m2并计算出新的阈值T=(m1+m2)/2，通过新的阈值T计算出新的数据集M和数据集I；

步骤4重复步骤2到步骤3，直到阈值T=T0为止。

传统密度峰聚类算法由于不能自动根据γ的区分簇中心和非簇中心，而采用手动选择聚类中心的方法，造成算法自动性差，主观性强，在某些数据集上也很难进行选点。本文提出使用迭代阈值法将聚类中心点自动选择出来，实现密度峰的自动聚类，提高了算法的自动化程度。

3 罚处共享最近邻密度峰聚类算法

3.1 算法描述与分析

本文所提算法的基本过程为：首先判断出罚处点，通过使用公式计算γ，对γ进行排序，并且通过迭代阈值找出簇中心，最后通过两次分配策略[4]分配样本点。

所提算法描述如下：

输入：数据集Xi={x1,x2,x3,…,xn}，K近邻个数k，罚处系数α

输出：聚类结果ψ={C1,C2,C3，…,Cm}(m为聚簇个数)

步骤1计算样本间的欧式距离形成距离矩阵Dn*n={dij}n*n；

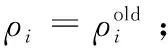
步骤4使用式(4)和式(5)计算δi；

步骤5使用式(6)计算决策值γi；

步骤6使用迭代阈值法，选出聚类中心。

步骤7分配确定从属点：

(1)初始化队列Q，将所有聚类中心点ψ={C1,C2,C3，…,Cm}加入队列Q；

(2)取出队列Q中的一点r；

(3)分配点r的邻居中的确定从属点，并将其加入队列Q；

(4)重复步骤7(2)和步骤7(3)直到队列Q为空为止。

步骤8分配可能从属点：

(1)寻找未分配的点并重新编号；

(2)形成分配矩阵M，其行对应于未分配的点的编号，列对应于簇；

(3)填充矩阵M；

(4)根据矩阵M对可能从属点进行分配；

(5)判断是否还有未分配的点，如果还有则令邻居数量k=k+1，重复步骤8(3)到步骤8(5)。

上述算法的一些关键细节说明如下：

(1)步骤7(3)中，可能从属点的定义和分配规则：如果r和r的邻居e的SNN的值大于k/2，即|SNN(r,e)|≥k/2，则定义e为确定从属点，如果e是确定从属点，则将其分配到r所在的簇中。

(2)步骤8(3)中，矩阵M的填充规则：对于所有未分配的点p，找到它所有邻居点q，判断q属于哪一簇，并在M中对p编号的行q所属簇的列数上+1，直到处理完p所有的邻居。重复填充，直到所有未分配的点全部处理完。

(3)步骤8(4)中，根据矩阵M对可能从属点分配规则：寻找矩阵M中的最大值，如果最大值大于0，则记录其出现的行和列，将行所对应的点分配到列所对应的簇上，直到M中的最大值等于0为止。

3.2 算法时间复杂度分析

计算SNN相似度(SIM)与传统SNN-DPC算法的时间复杂度相同为O(kn2)，计算δ和ρold为O(kn2)；计算ρ时的复杂度小于O(kn)；γ需要进行排序，对其排序的时间复杂度为O(nlogn)；进行迭代阈值时的复杂度为O(n2)；两次分配策略需要O((k+m)n2)的时间复杂度，因此所提算法的时间复杂度为O((2k+m+1)n2)，与传统SNN-DPC算法同处一个数量级。

4 仿真实验

仿真实验的计算机硬件环境为Intel Pentium Gold G5400 (3.7 GHz) CPU，内存8 GB。在Windows10 x64平台下使用MATLAB R2019a实现所提算法。

4.1 实验数据集说明

本实验使用了5个人工数据集、6个UCI真实数据集、2个图像数据集，数据集的详细情况见表1到表3。

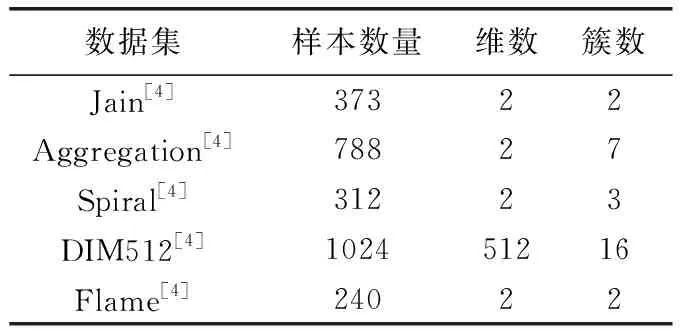
表1 实验用的人工数据集

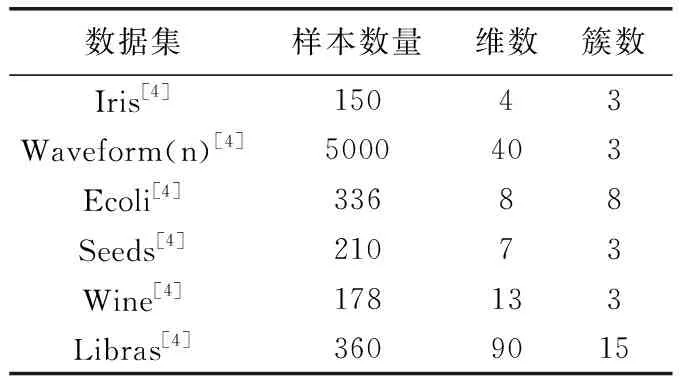
表2 实验用的UCI数据集

表3 实验用的图像数据集

4.2 人工数据集上的实验结果及分析

本文算法与原始SNN-DPC算法[4]在人工数据集上的比较如图1到图6所示，圆圈代表决策图中正确的聚类中心；结果图中聚类中心使用星星标出，经过聚类被分为同一簇的拥有相同的图案。

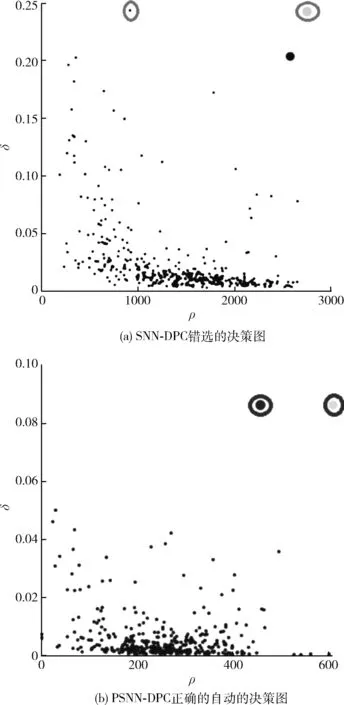
图1 两种算法在Jain数据集上决策图的对比

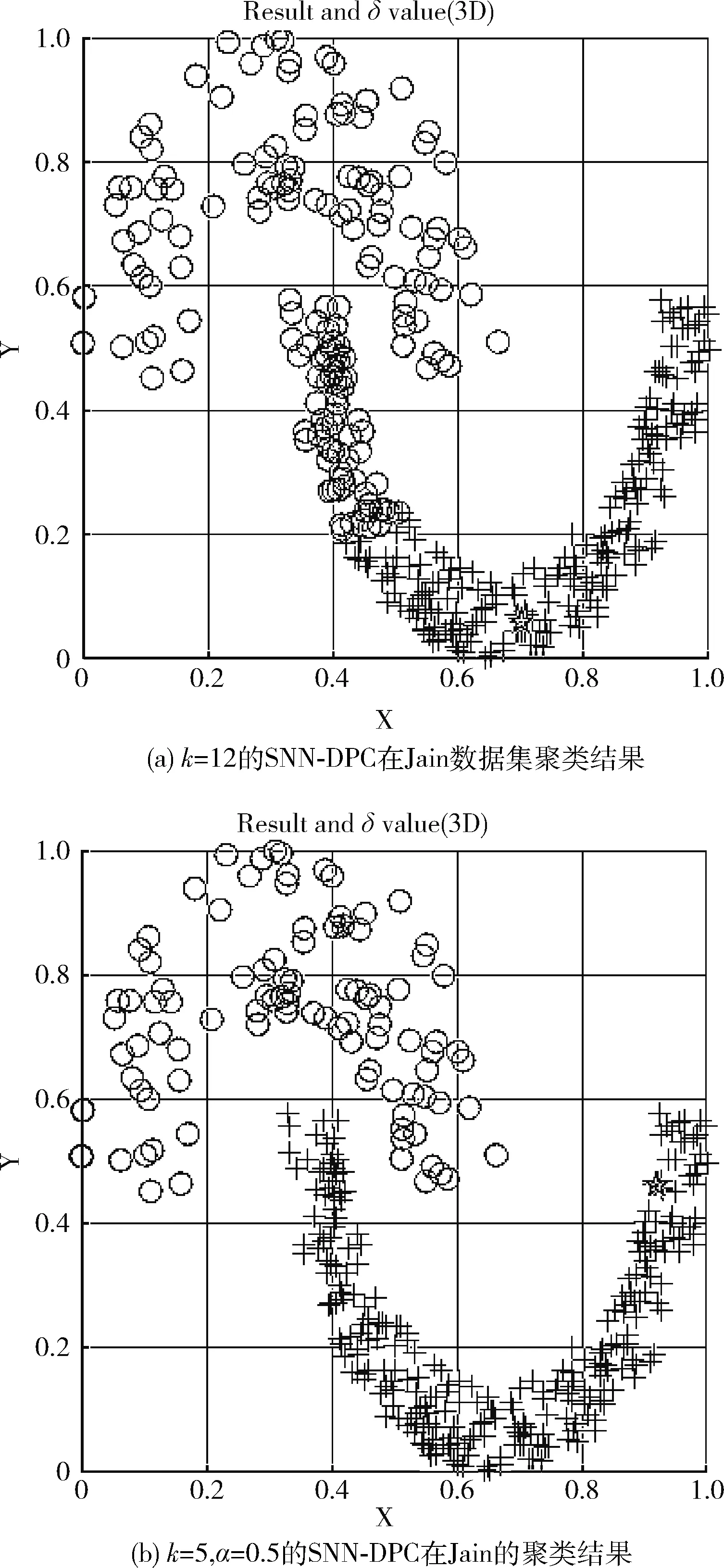
图2 两种算法在Jain数据集上聚类效果的对比

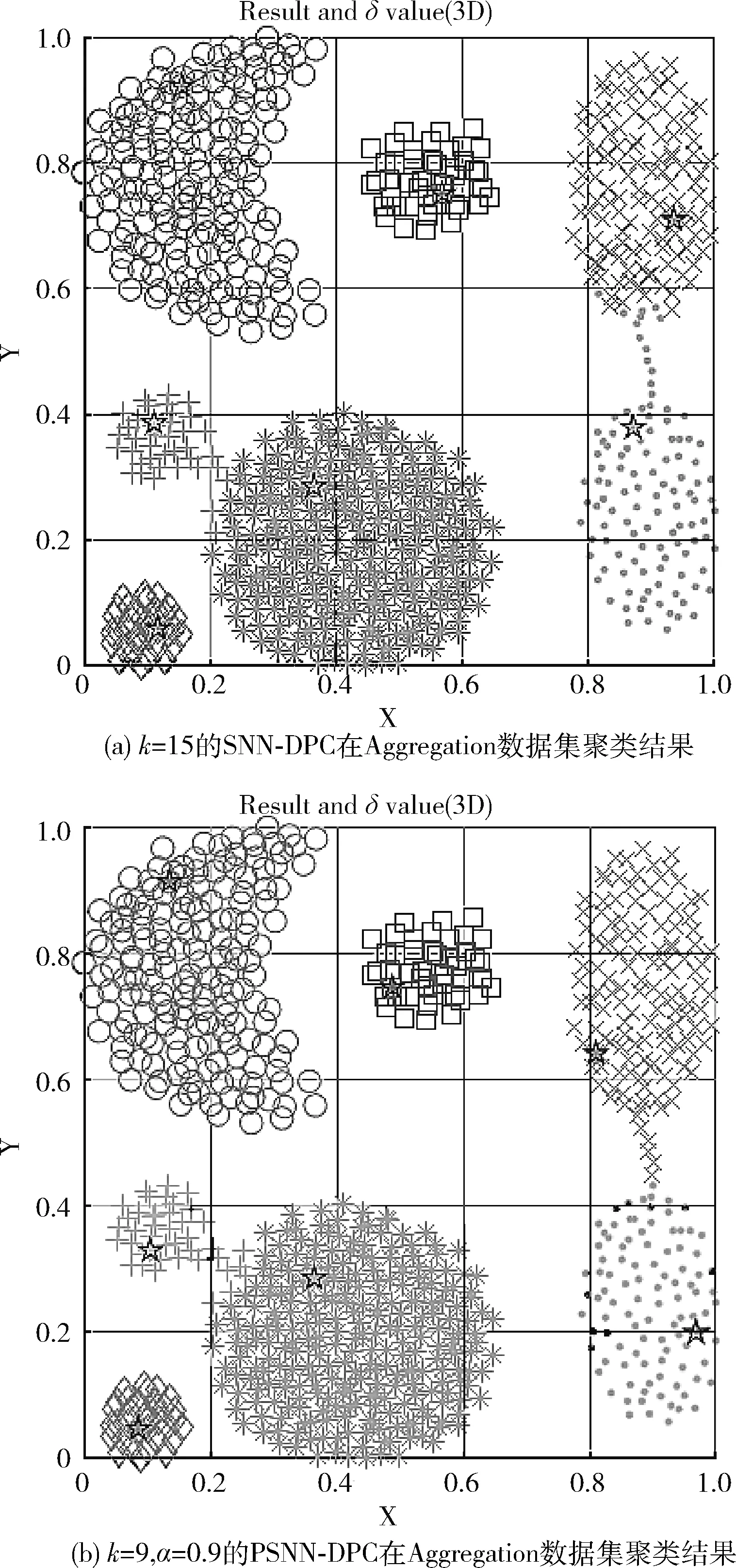
图3 两种算法在Aggregation数据集上聚类效果的对比

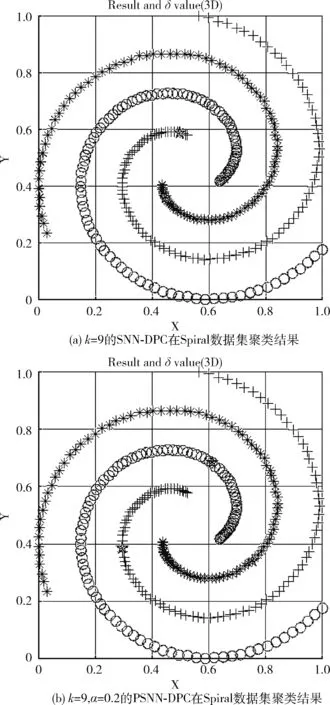
图4 两种算法在Spiral数据集上聚类效果的对比

图1为SNN-DPC和PSNN-DPC的决策图对比，从图1可看出：由于SNN-DPC没有对高密度中心点进行罚处，导致其决策图右上角的两个点并不全是真正的聚类中心，SNN-DPC将其错选为聚类中心；而PSNN-DPC引入了罚处策略，决策图中右上两点即为正确的聚类中心，从而能选出正确的聚类中心。图2显示，SNN-DPC把两个聚类中心点都选择在密度较大的簇上，忽略了密度较小簇的聚类中心，出现了错选聚类中心点的问题，导致聚类出错；而PSNN-DPC引入了罚处和迭代阈值法后，可以正确自动选择聚类中心，没有忽略密度较小的簇中的聚类中心，可以正确的将其分为两簇。对此问题，SNN-DPC[4]采取的办法是用非常规方法选点，选相对距离较高的点，而不选其算法中γ较高的点，这种方法不具备普适性，且主观性大，不能实现自动化选中心点。

根据图1和图2，PSNN-DPC中的罚处策略可以有效地将低密度簇中的聚类中心显露出来，进而对密度分布不均的数据具有良好的聚类效果。

图3的聚类结果对比显示，在每个簇不同形状差异的数据集Aggregation中，PSNN-DPC和SNN-DPC都能正确识别聚类中心，但PSNN-DPC较原始算法有所提升，体现簇的边界方面。SNN-DPC会在将部分边界区域较多的错分，而改进的PSNN-DPC算法错分的数量较小。反映在指标上的是，原SNN-DPC算法的AMI为0.9500而PSNN-DPC的AMI为0.9687，提升了大约2%；虽然幅度不大但是PSNN-DPC是自动选择聚类中心的；而原始算法是需要手动选择聚类中心的。图4的聚类结果对比显示，在Spiral数据集中，PSNN-DPC和SNN-DPC都能准确地识别簇，验证了本文算法在环形数据中具有良好的聚类效果。

图5的聚类结果对比显示，由于DIM512数据集具有较高的维数和较多的簇中心，给自动识别簇中心带来了一定难度，但PSNN-DPC依然表现了良好的效果，正确识别了聚类中心且发现16簇，聚类结果完全正确。这说明本文算法不仅能处理簇数量小维数低的数据，在簇数量多、维数高的情况下，依然能准确地自动地识别聚类中心和簇数，具有良好的普适性。

图6的聚类结果对比显示，在Flame数据集中，PSNN-DPC较SNN-DPC有较大的优势，虽然两者都正确的聚类中心和两簇，但PSNN-DPC的AMI达到了0.9615，较SNN-DPC的0.8975提升了近7%，能够准确地将该数据集分为两类。这说明本文引入罚处思想和迭代阈值后，边界点归属的划分准确性提高，所提的改进思路是有效的。

从这5个在模拟数据集中的聚类结果我们可以发现，PSNN-DPC算法不仅仅可以自动地准确地确定聚类中心，增加算法的自动化，而且由于引进了罚处思想，使得低密度簇中的密度中心得以显露，由此聚类效果更加准确，解决了传统SNN-DPC算法中的问题。

4.3 UCI数据集上的实验结果及分析

本文将对PSNN-DPC和其原始算法(SNN-DPC)、经典密度算法DBSCAN以及DPC算法和其近年来改进的其它DPC改进算法，如WDPC[7]、DPC-CP-GS[8]进行对比，结果采用AMI[11]、ARI[12]进行量化对比，其取值范围皆为[-1,1]，值越大代表聚类结果与真实情况越吻合，AMI和ARI的特点是可以衡量极端情况下的聚类效果，如果一个方法聚类效果相比随机分配都不如，其值可以为负数；这相比传统的ACC等指标更能准确反映聚类效果。实验结果见表4和表5。表中的符号“-”表示文献未给出该指标的结果。

图5 两种算法在DIM512数据集上聚类效果的对比

图6 两种算法在Flame数据集上聚类效果的对比

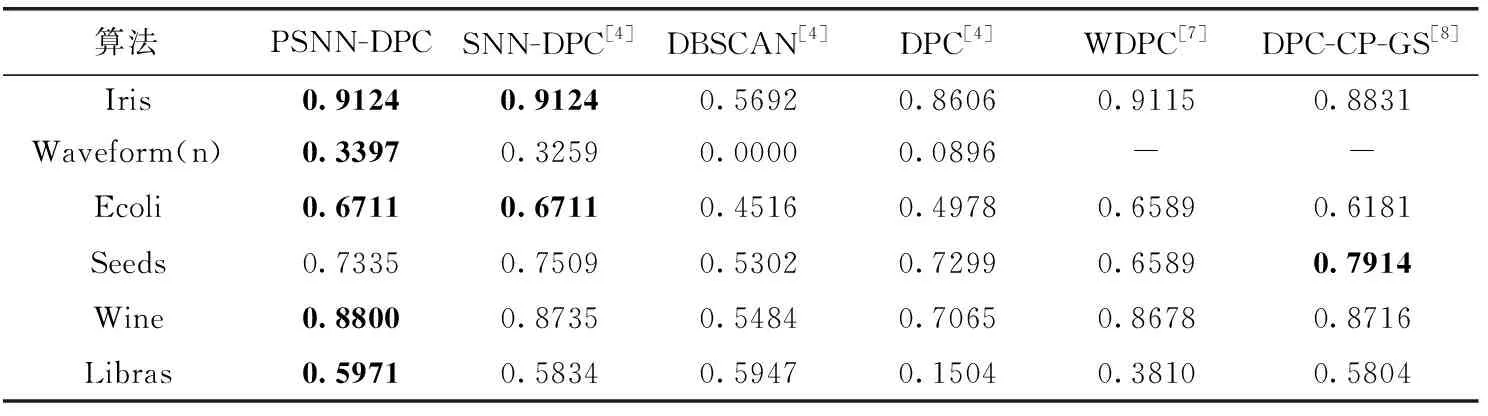
表4 各算法聚类结果AMI指标的对比

表5 各算法聚类结果ARI指标的对比

通过表4和表5的结果分别进行分析：

在最常用的Iris数据集中，本文算法较SNN-DPC算法持平，均为实验中算法里最好的，对比其它算法，PSNN-DPC在该数据集中其聚类效果最高有60.3%的提升，平均也有10%的提升。

在噪声比较多样本数量大且维数较大的Waveform数据集中，由于本文所提算法具有罚处的特性，使得在该数据集中较SNN-DPC算法提升了4%，对比其它算法有更大的优势，是所有实验算法中效果最好的，验证了PSNN-DPC算法不仅仅能自动找出聚类中心，还能拥有良好的聚类效果。

在大肠杆菌Ecoli数据集中，其与原始SNN-DPC算法并列第一，均具有良好的聚类效果，相比其它聚类算法具有至少2%的提升。

在种子Seeds数据集中，本文算法与其它两种算法相比略差，但是差距不是很大，也说明本文算法依然还是需要改进。

在具有13个特征的Wine数据集中，本文算法表现出了良好的聚类，较SNN-DPC算法有所提升，较DPC算法具有60.5%的提升，平均也有13.7%的提升，验证罚处思想在聚类中具有一定的优势。

在Libras数据集中，本文AMI指标较原始SNN-DPC算法有所提高，也领先于其它算法。

综上所述，本文所提算法的聚类效果在大多数UCI真实数据集上优于其它算法，这说明引入迭代阈值法和罚处思想，不仅可以准确无误地自动找出簇中心，还可以有效地减少低密度中心点被忽略的机率，提高簇中心点选择的准确度和样本点分配的准确率。

4.4 图像数据集上的实验结果及分析

聚类分析的一个重要方面是进行图像聚类，本文使用了一个物体数据集Coil-20和人脸数据集Olivetti face进行实验。因图像的维数较高，所以聚类前需要用降维方法来预处理数据。我们采用PCA法对图像进行降维，并且只过滤累计90%的主成分[13]，这样可以有效地降低维数并且可以降低噪音。我们将实验结果与手动的SNN-DPC作对比，结果见表6。

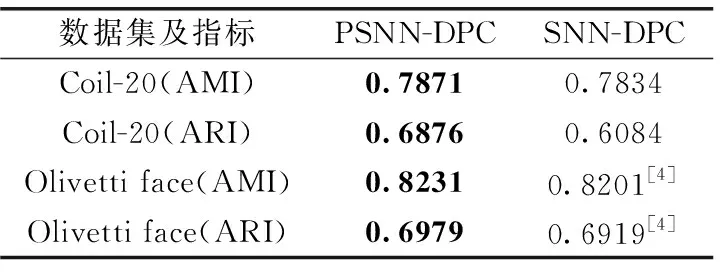
表6 SNN-DPC与PSNN-DPC在图像数据集中的对比

Coil-20是一个物品图片集合，其包含对20个物体从不同角度的拍摄，每隔5度拍摄一副图像，每个物体72张图像[14]。从表6可知，PSNN-DPC算法在该数据集中聚类结果的各项指标都优于SNN-DPC，其中ARI指标领先幅度较大，提升了约13%。Olivetti face数据集包含1992年4月至1994年4月之间在AT&T剑桥实验室拍摄的一组面部图像，数据集共有40个人，每个人具有10张不同的照片，由表6的结果可知，PSNN-DPC算法较SNN-DPC也有略微优势。根据这两组物品和人脸数据集的结果，PSNN-DPC在图像数据集中聚类是有效的，所提算法对图像数据聚类有良好的效果。

5 结束语

针对大多数密度算法容易忽略低密度簇和不能自动选择聚类中心的问题，本文在SNN-DPC算法的基础上提出一种罚处共享最近邻密度峰聚类算法，利用罚处思想使高密度簇非聚类中心的局部密度变小，令低密度簇中的聚类中心得以显现；迭代阈值思想可以通过阈值将数据分为普通点和簇中心点。人工数据集和UCI真实数据集以及图像数据集上实验结果表明所提算法是可行的、有效的。