借助抽象思维 解答数学难题

陈勇华

(福建省连江华侨中学 350599)

图像是将考察对象抽象后的产物，是最先使用的数学语言，也是直观形象的语言，文字语言是对图像的描述解释与讨论.符号语言则是对文字语言简化和再次抽象的产物.教学中应结合具体例题的讲解促进三种语言的科学转化，以更好的提高学生的解题能力与解题效率.

一、“图像语言向符号语言转化”在解题中的应用

如图1，四面体A-BCD的四个面均是直角，若AB⊥平面BCD，BD⊥CD，AB=BD=CD，AC上存在一动点P.若CP的长度为x，△PBD的面积用f(x)表示，则f(x)的大致图象为( ).

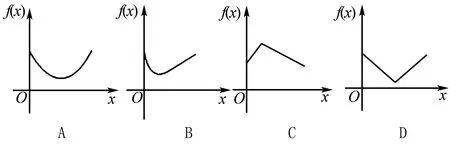
图1

该题为立体几何题目，难度中等.解答该题需要根据题意由图像语言转化为符号语言论证图像中线与线、线与面之间关系，找到相关参数之间的内在关联，而后通过类比进行作答.过点P作PF∥AB交BC于点F，过点F作FE∥CD交BD于点E，连接PE，如图2.

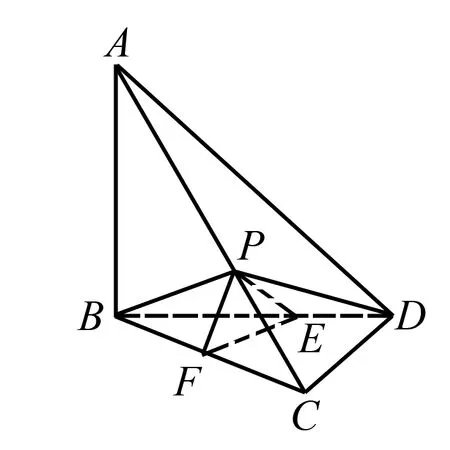
图2

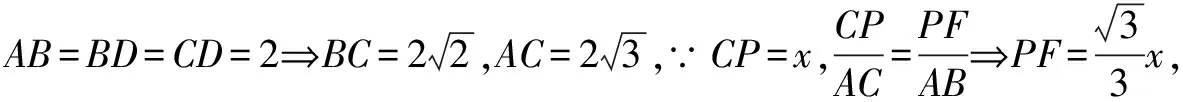
二、“符号语言向图像语言转化”在解题中的应用

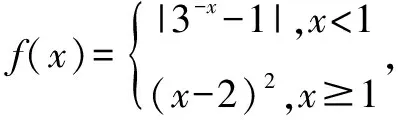
A.(2，3) B.(4，5) C.(4，+∞) D.[4，5]

该题为分段函数题目，考查学生画函数图象的熟练程度，难度中等.解答该题需要认真审题，合理的抽象将符号语言转化为图像语言.结合图像寻找相关参数的取值范围.根据题意，画出函数f(x)的图象，如图3所示：

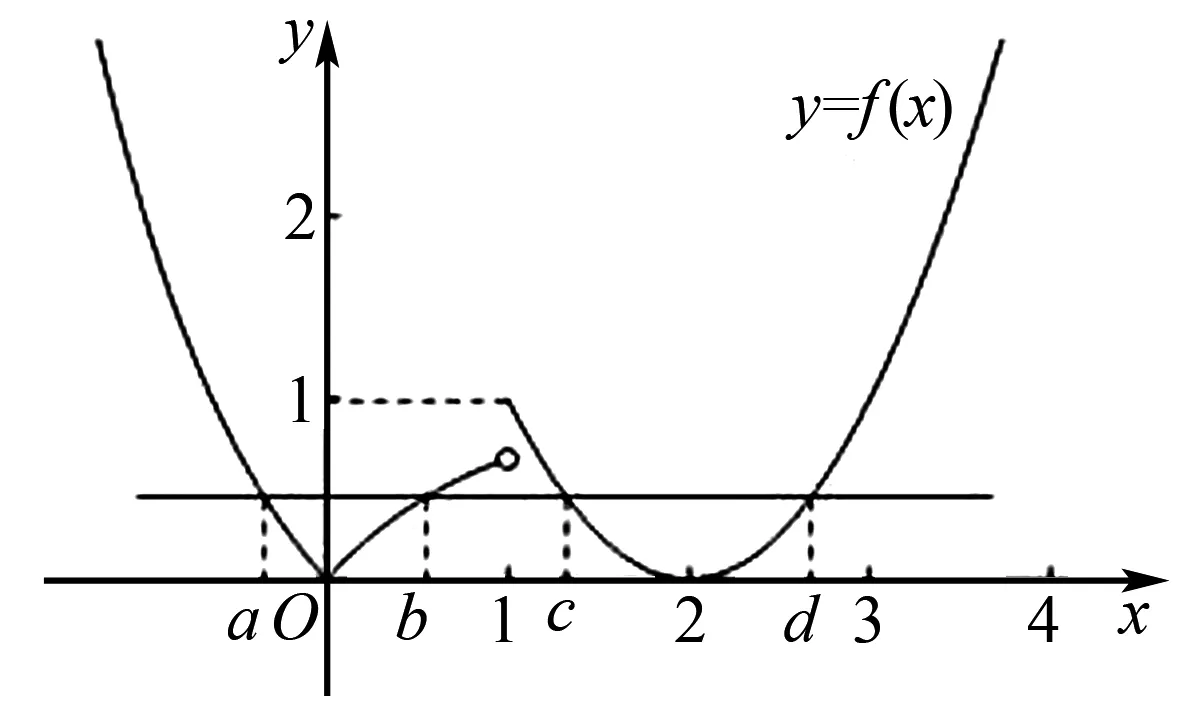
图3

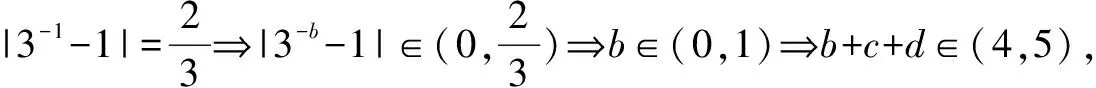
三、“文字语言向图像语言转化”在解题中的应用

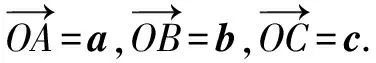
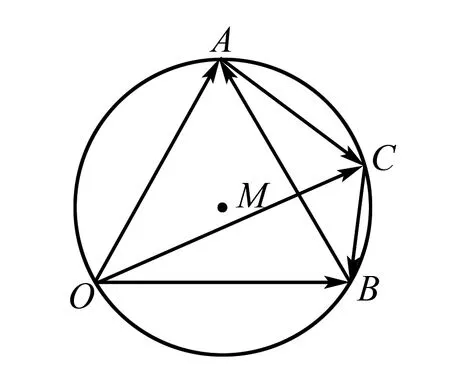
图4

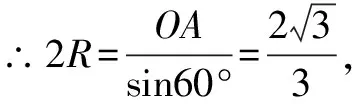
四、“文字语言向符号语言转化”在解题中的应用

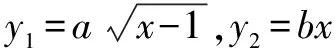
高中数学教学充分吃透数学抽象的内涵，把握数学抽象在教学中的具体体现，通过相关理论的灌输以及例题的讲解，从而使学生把握数学抽象的具体表现形式，掌握在不同的问题情境中进行合理抽象，这样，则可以大大提高其解题能力的同时，还能顺利完成核心素养的培养目标.