风洞分布式支撑天平测力试验技术研究
闫万方,张晨凯,蒋坤,张江
(中国航天空气动力技术研究院第二研究所,北京100074)
0 引 言
目前,风洞测力试验多以单台天平尾支撑或腹/背支撑的方式进行,其特点是气动载荷传递路径单一,测量误差小。随着航空航天技术的发展,新型布局飞机、箭弹等型号研制层出不穷,传统单天平支撑测量方式已经无法满足某些型号高精度测力需求。民用飞机测力试验中,常规单尾支撑、腹/背支撑方式对阻力及俯仰力矩测量精度影响较大,支撑干扰修正困难;双机身飞机等新布局飞行器测力试验,单天平支撑方式存在非对称支撑导致的测量载荷严重不匹配、天平载荷容量受限以及单侧支撑干扰无法消除等问题。近年来,针对不同试验需求,国内外风洞研究机构开展了分布式支撑试验技术研究。国外,S. Marija等针对某飞机试验发展了分布式外置天平测力试验技术,利用6 个外置单分量力传感器组成测力平台,实现气动力测量;T. Milan 等也采用类似技术实现机翼三分量气动力的精确测量。国内,Liu Bokai 等针对某高超声速飞行器风洞试验开发分布式悬浮天平测力系统,相比采用内式单尾支撑天平测力方法,测力系统的刚度和分辨率显著提高,获得了较好动态测量效果。上述分布式支撑测力试验技术均采用外置天平分布式测量方法,即利用在风洞试验模型外部多个自由度设置单分量天平方式实现测量。
采用双尾支撑测量形式,其主要难点在于:一是模型—多支撑天平系统组装后处于过约束状态,加工、装配误差会使系统内应力过大,致使系统整体刚度、传力路径及天平灵敏度等发生变化,从而导致测量偏离真实状态甚至试验失败;二是分布式天平地面静态校准方法,直接影响了系统的测量精度。
本文基于某双机身飞机测力试验,以6 分量天平双尾支撑测量为例,发展多维力天平内置的分布式支撑天平测力试验技术;设计可实现双天平之间位姿微调的双支撑测量系统,解决系统内应力过大问题;提出两种6 分量双支撑天平校准及测力方法,分别进行校准和加载验证。
1 试验需求及测力系统
1.1 双体飞机CTS 试验
在中国航天空气动力技术研究院(CAAA)的FD-12 风洞进行某双体无人机空射平台挂弹轨迹捕获(CTS)试验,如图1 所示,分别测量机—弹分离后挂弹受载、运动轨迹以及载机受挂弹轨迹干扰受载情况。与以往试验不同,本试验载机为双机身布局飞机,传统单天平支撑测力方式存在单侧支撑干扰无法消除、非对称支撑导致的测量载荷严重不匹配等问题,无法满足载机载荷精确测量需求。针对这一问题,采用双支撑天平测力形式,通过解决双支撑天平固有内应力问题及校准、测量方法,实现载机干扰载荷准确测量。

图1 某双体无人机空射平台挂弹CTS 试验Fig.1 CTS wind tunnel experiment for missile using a double-body airplane as lunch platform
1.2 双支撑天平测力系统
双支撑天平测力系统如图2 所示,主要包括双体载机模型、双天平、双尾支杆、后端双支撑接头和位姿微调装置。由于双体载机气动布局的特殊性,为尽可能提高载机载荷测量精度,兼顾CTS 并联运动机构的轨迹空间需求,载机模型支撑方案采用“双机身—双尾支撑”的形式。两台天平分别置于双机身内,载机模型通过双支撑天平系统最终固支于风洞支架上,实现气动载荷测量。其特点是支撑刚度大,测量干扰小,支撑装置组装方便,误差可控。双支撑天平系统与CTS 运动机构在所有试验工况下均不发生空间干涉,可实现载机—挂弹分离后载机受挂弹轨迹干扰的6 分量气动载荷准确测量。

图2 双支撑天平测力系统示意图Fig.2 Schematic diagram of the twin-sting-balance aerodynamic force measurement system
双支撑系统的研制是本项试验的关键之一,需具备位姿微调功能,以消除模型—天平系统装配时固有的过约束以及加工、装配误差而导致的系统内应力。针对这一问题,设计双支撑天平系统位姿微调装置,如图3 所示,主要包括双尾支杆、支撑转接、楔形调整块和双接头。双尾支杆分别安装于方形支撑转接上,并采用专用螺母紧固;两支撑转接分别装入双接头的两侧接口,通过楔形调整块胀紧紧固,组成双支撑系统。

图3 双支撑系统位姿微调装置Fig.3 Position and attitude adjustment device of the twin-sting-balance measurement system
微调装置的调整原理如图4 所示,结合图3,安装两支撑转接的双接头两端接口内分别留有沿纵向和侧向调整间隙,与两支撑转接配合安装的两组楔形调整块分别沿纵向(上、下)和侧向(左、右)对应位置对称布置,通过对单侧楔形调整块施加不同预紧拉力,可实现双尾支杆之间纵向和侧向相对位姿微调;两支撑转接在楔形调整块胀紧前可沿轴向自由移动,实现双尾支杆相对轴向位置微调;另外,尾支杆与支撑转接之间通过“键”实现滚转定位和微调。模型—双支撑系统组装时,通过判断组装前后两天平零点变化实现双支撑系统位姿微调。实践表明,该设计可有效消除双支撑天平系统装配应力。

图4 调整原理Fig.4 Adjustment principle of the measurement system
1.3 天平设计
双支撑天平测力系统需研制,并按照图纸加工两台相同的天平,以减小由于天平间差异而导致的测量误差。单台天平设计载荷如表1 所示,综合考虑模型尺寸约束、天平灵敏度、强度/刚度要求等,天平最大直径为22 mm。

表1 单台天平设计载荷Table 1 Design loads of a single wind tunnel balance
不同于单天平测力,双支撑天平测量传力路径复杂。例如,模型受载偏航力矩M
时,大部分载荷以双天平受轴向拉力、压力形式承受,这与单支撑天平受载传力有质的区别;另外,由于模型受载变形,单台天平还需承受整个系统内力,天平受力更为复杂。双天平研制需尽量减小分量间测量干扰。本文新研制天平采用文献[11]所述的天平结构形式,最大程度减小各分量尤其是轴向力的测量干扰,双天平实物图如图5 所示。
图5 天平实物图Fig.5 Real photo of the wind tunnel balance
2 校准及测力方法
双支撑天平测力试验技术的另一关键是天平系统的校准及测力方法。本文提出两种6 分量双支撑天平方法:“合成式校准测力”方法和“广义式校准测力”方法。
合成式方法需分别对两台天平采用同样方法校准,较繁琐;另外,若要获得较高的测力精度,对系统中天平相对位姿、内应力水平等要求较高。广义式方法将系统当作广义天平校准,对系统装配要求较低,且校准相对简单,但对校准架的校准能力要求较高,需确保校准系统和试验系统保持一致,即双天平系统校准完成后不能再次拆装,通用性差。
2.1 “合成式校准测力”方法
2.1.1 数据处理方法
“合成式校准测力”方法是将双支撑天平分别视作独立测量个体,采用相同的方法校准分别获得天平公式,风洞试验时,将两天平的独立测量载荷通过坐标系转换合成到模型坐标系下,即可获得模型的气动载荷。双天平坐标系及合成坐标系如图6 所示,双天平与模型连接视为刚性连接,合成坐标系即为模型坐标系。

图6 双天平坐标系及合成坐标系示意图Fig.6 Coordinate systems of the twin-sting-balance and combination model
“合成式校准测力”方法流程图如图7 所示。

图7 合成式校准及测力流程Fig.7 Calibration and force measurement process of the combination method
具体测量方法及步骤如下:
(1)分别对单台天平实施静态校准,校准公式由式(1)给出,式中,i
=1,2,…,6。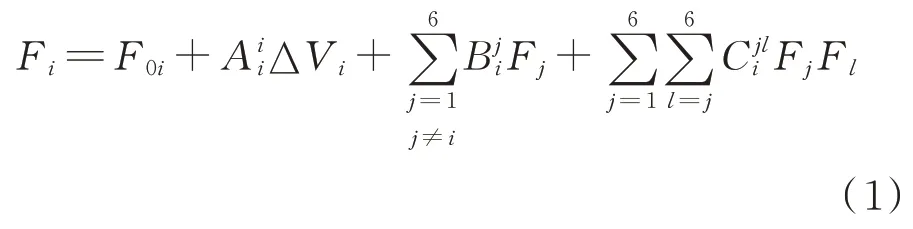
φ
和φ
。(3)实施风洞试验,获得双天平的体轴系载荷,分别记为F
[Y
,Z
,X
,M
,M
,M
]以及F
[Y
,Z
,X
,M
,M
,M
]。(4)将双天平的体轴系载荷通过式(2)分别转换至双天平坐标系O
-X
Y
Z
和O
-X
Y
Z
下,记为F
[Y
,Z
,X
,M
,M
,M
]及F
[Y
,Z
,X
,M
,M
,M
],其中,i
=1,2。
F
[Y,Z,X,M,M,M
],即试验时模型的气动载荷。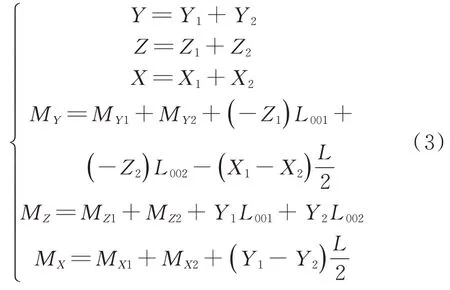
L
为两天平轴线之间的距离;L
和L
为两天平校准中心与合成坐标系原点的轴向距离。2.1.2 校准结果及加载验证
首先,对双天平分别进行复位补偿型体轴系校准,获得单台天平体轴系校准公式;其次,对“合成式校准测力”方法合理性进行检验加载验证。基于双支撑天平系统检验加载装置,进行“广义式校准测力”方法研究,并开展对比分析验证。上述工作在CAAA 的ABCS-300 型校准架上进行。
单天平校准及双支撑天平系统检验加载载荷如表2 所示,检验加载载荷依据试验模型预估而定。单天平静态校准及标模试验(ADA-028324 8#标模在Ma
=2.0 时的重复性精度)结果如表3所示,可以看出:新研制天平各分量具有良好的测量重复性和较小测量误差,尤其是轴向力分量,综合加载误差和综合加载重复性精度达到了国军标GJB 2244A-2011中的先进指标要求;两天平的标模试验结果良好,重复性精度满足风洞试验指标要求。
表2 天平校准、检验加载载荷Table 2 Calibration and check loads of the balance

表3 单天平静校精准度、标模试验精度Table 3 Static calibration and standard model experiment accuracy of the balance
双支撑天平系统检验加载平台如图8 所示。为满足校准架空间限制要求,设计相应专用校准支杆、专用6 分量加载装置,用于实现双天平系统的受载模拟,同时,该装置也用于“广义式校准测力”方法研究。专用加载装置安装在试验模型上,加载坐标系与模型(合成)坐标系重合。基于该校准装置,结合2.1.1 节所述的数据处理方法,进行双天平单分量检验校准、多分量组合检验校准等,对两台天平的校准公式、合成校准及测力数据处理方法以及双支撑天平系统可靠性进行验证。

图8 双支撑天平系统检验校准Fig.8 Calibration and validation of the twin-sting-balance measurement system
单分量施加检验载荷时双支撑天平系统测量载荷与加载载荷对比如表4 所示,可以看出:各分量测量相对误差均在0.3%以内,测量精度较高,尤其是纵向分量M
和Y
,相对测量误差均在0.1%以内。多分量检验加载的综合加载误差和综合加载重复性结果(二者均指相对于满量程校准载荷)如表5 所示,可以看出:采用“合成式”方法的各分量综合加载误差均优于0.5%,其中,力载荷Y
、Z
、X
误差均在0.2%以内,误差水平与单台应变天平测量误差水平相当,满足风洞试验需求,表明“合成式校准及测力”方法可行;双支撑天平系统的综合加载重复性误差优于0.1%,几乎达到了国军标GJB 2244A—2011 中的先进指标要求,表明系统各部分连接、测量可靠。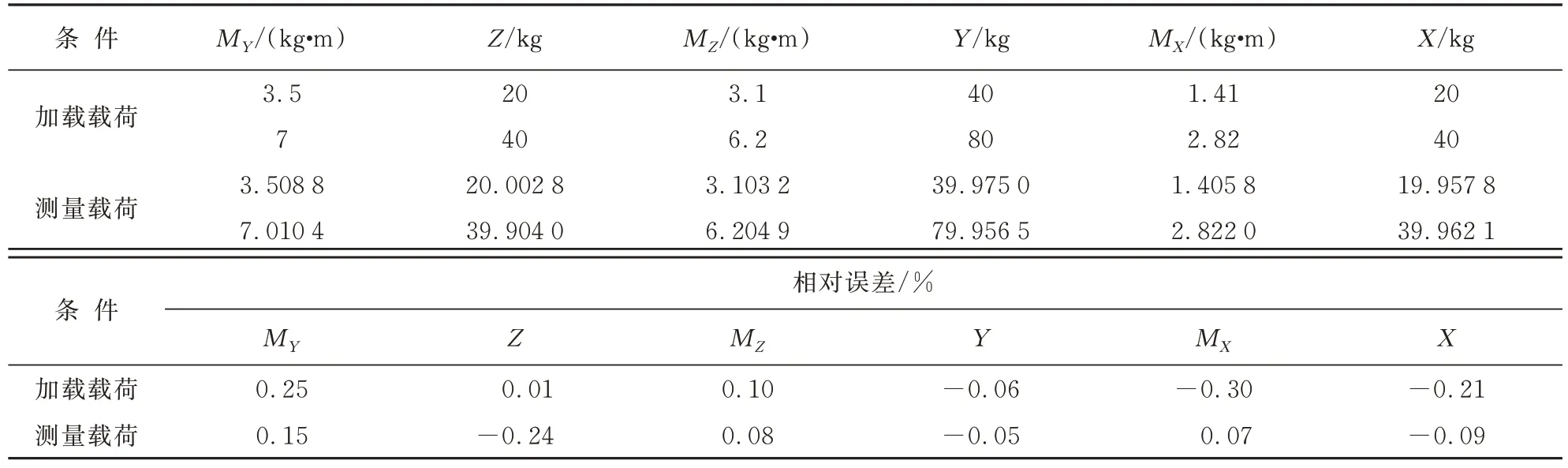
表4 单分量检验加载数据Table 4 Validation data of single component
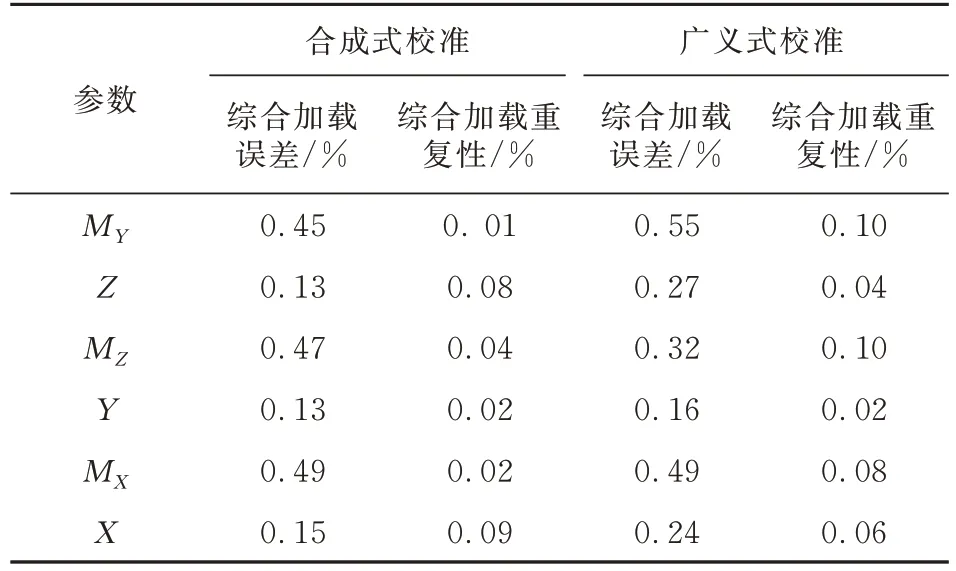
表5 综合加载分析Table 5 Comprehensive calibration analysis
2.2 “广义式校准测力”方法
基于2.1.2 节所述的双天平检验加载装置,本节给出“广义式校准测力”方法。将双支撑天平系统作为测量整体,即将双天平系统视为一个广义天平,采用神经网络法对该广义天平进行校准可获得广义天平公式。利用校准样本点对网络进行学习/训练并建立神经网络数学模型,将12 路天平信号输出作为网络模型输入,网络输出即为期望的6 分量气动载荷。此方法对系统装配要求较低,且可作为常规天平实施校准;但需校准系统和试验系统保持一致,即双天平系统校准完成后不能再次拆装。若校准设备可满足双支撑天平系统的广义式校准,则该方法也可优先选用。
神经网络是指用大量简单的计算神经元构成的非线性系统,对于求解此类非线性广义天平系统测量问题具有良好的响应能力。“广义式”校准方法采用的神经网络模型如图9 所示,12 路天平电压信号作为模型输入层,6 路测量气动载荷作为模型输出层;隐含层和输出层的传递函数分别为正切S 型传递函数和线性传递函数;通过网络学习/训练和优化,隐含层和输出层的节点数分别为9 和6;经上述设置和训练,该网络模型可获得较高的模拟精度。需要说明,利用神经网络法获得广义天平公式,相比而言没有实际物理意义。

图9 广义式校准神经网络模型Fig.9 The neural network model of the integration calibration method
共选取16×8=128 组载荷作为校准样本点来训练网络模型,采用与2.1.2 节相同的检验载荷作为网络模型检验点,用于检验神经网络模型的精度,并与“合成式”方法进行对比分析。
采用神经网络法对双支撑天平系统进行校准的6 分量载荷样本点及相应网络模型误差分布如图10 所示。

图10 广义式校准样本点及相应网络模型误差分布Fig.10 Sample points and network model error distribution of the integration calibration method
从图10 可以看出:利用训练好的网络模型反算得到的样本点载荷误差带较小,侧向M
、Z
误差在±1.2%以内,纵向M
、Y
误差在±0.6%以内,轴向M
、X
误差在±0.8%以内,这与采用多项式拟合方法的常规天平校准样本点误差带统计水平相当,表明通过训练/学习和优化,该神经网络模型对双支撑天平系统的测量模拟精度已经达到较高水平。两种校准方法获得的同一检验载荷误差分布对比如图11 所示,其中Comb_calibration 为“合成式”校准方法,Integ_calibration 为“广义式”校准方法。检验载荷由17 组组合载荷组成,前7 组载荷相同,重复施加7 次,用于检验测力系统重复性测量精度(图11 中灰色显示部分),后10 组载荷用于检验测力系统的综合加载误差(图11 中其他部分)。
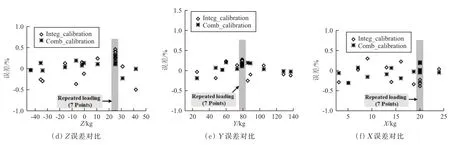
图11 两种校准方法检验校准载荷误差对比Fig.11 Check loads error comparison of the two calibration methods
从图11 和表5 可以看出:两种校准方法对于同一组检验载荷的相对误差水平相当,即对双支撑天平系统采用广义式校准也可达到与组合式校准相当的测量精度。
3 双体飞机风洞试验
综合考虑现有校准设备能力(空间)限制,最终采用“合成式校准测力”方法进行风洞试验。典型试验状态下(侧滑角β
=0°,攻角α
为 0°~1.6°),载机的俯仰力矩M
、法向载荷Y
和轴向载荷X
随攻角α
的变化曲线如图12 所示。图中分别给出了该状态下单台天平的受载以及载机气动载荷情况,其中,图例‘Balance1’和‘Balance2’分别为两天平分别受载,‘Comb_Model’为载机的真实受载。从图12 可以看出:双支撑天平系统中的两台天平的承载和测量呈现出了较好一致性。通过风洞试验,进一步验证了本文试验系统和校准、测量方法的可靠性,以及双支撑天平测力方法对于解决此类问题的可行性。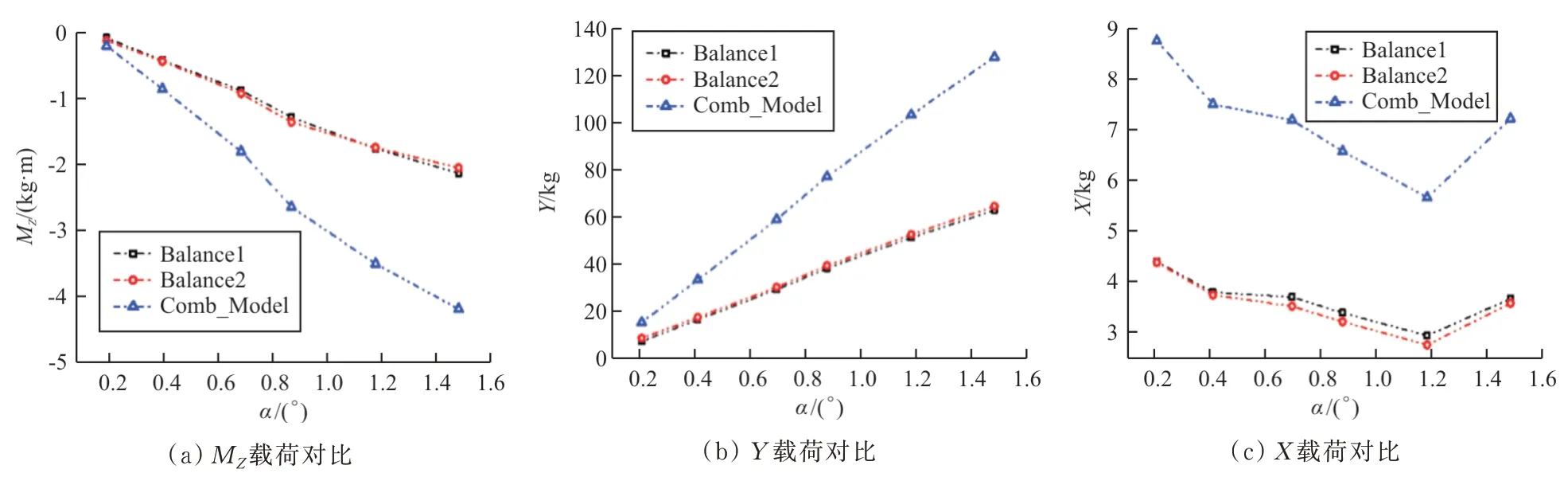
图12 典型状态下双天平和载机的气动载荷Fig.12 Aerodynamic loads of the double-body airplane and balances in typical fly condition
4 结 论
(1)针对双支撑天平测力存在模型—天平系统装配时固有的过约束以及加工、装配误差而导致系统内应力较大的问题,研制了具有消除系统内应力功能的双支撑天平系统,并给出微调原理和方法,该系统可有效消除双支撑天平系统装配内应力。
(2)提出两种校准测力方法:“合成式校准测力”和“广义式校准测力”方法,并实施校准研究和对比验证,双支撑天平系统各部分连接可靠,测力方法可行,测量误差与单台应变天平水平相当,可满足风洞试验测量精度需求。
(3)最终采用“合成式校准测力”方法进行风洞试验,取得了良好测量效果。需要说明,本文所述分布式支撑天平测力试验技术不限于双天平测量,也可拓展为多支撑天平(大于3)试验技术。

