先进战斗机纵向飞行特性与放宽静稳定度研究
皇甫乃章 ,杨蓓 ,但之华 ,孙鹏辉
(1.南昌航空大学飞行器工程学院,南昌330063)
(2.上海宇航系统工程研究所一室,上海201109)
(3.北京航空航天大学能源与动力工程学院,北京100191)
0 引 言
面对复杂的战场环境,先进战斗机通常会从减少被探知概率和增加机动能力两个方向对飞机整体进行优化提升以提高战场生存能力,这在一定程度上改变了飞机的气动布局、重量分布和控制方式,使先进飞机的稳定性特性相比传统飞机有较大的差别。
飞机稳定性是表征飞机在受到扰动之后能否自动返回原本稳定状态的特性,分为静稳定性和动稳定性。静稳定的飞机不一定具有动稳定性,但静稳定是飞机动稳定的前提,与真实的稳定性密切相关。静稳定的飞机能够在较少外部控制下保持稳定可靠的飞行状态,但过度稳定的飞机会导致做机动时需要更大的操纵力矩和更长的响应时间,影响飞机的机动性能。
B. C. Anderson、R. W. Klein 等、L. Pasley等提出将放宽静稳定技术与机动载荷控制技术相结合来改善战斗机机动性能的方案;在此基础上,李立等、马界祥等和 J.Kalviste分别从气动力学出发分析放宽静稳定度对翼面气动力的影响;K. Wilhelm 等、郑遂等研究了放宽静稳定对飞机动 态 性 能 的 改 变 ;Yan Jianning 等、B.Newman 等、T.Wagner 等就如何更好地利用放宽静稳定度在飞机机动性方面优势的控制方法进行了大量研究。不再满足于将放宽静稳定设计只是作为飞机设计的优化环节,而将其引入到飞机概念设计阶段,即从飞机设计初期就加入稳定性控制的观念,从而跳出传统最小稳态裕度的严格限制,使飞机设计师有更大的设计空间。放宽静稳定技术及相应的主动控制技术,在更多的飞行器领域得到研究和应用,比如,在民用航空领域利用其提升经济效益;在隐身性能优秀的飞翼飞机上,利用其改善机动能力和可操控性能,空空导弹利用其来提升近距离格斗能力等。由于传统飞机整体气动布局设计求变的大趋势以及飞行控制技术的发展,先进战斗机采用放宽静稳定度的主动控制技术成为一种必然。要进一步发展放宽静稳定度的主动控制技术,就需要对放宽静稳定带来的飞机动态特性的影响有更全面的认知。
常用的放宽静稳定度的方式有两种,一种为固定重心位置,前移焦点位置,这涉及到改变飞机的整体气动布局,耦合因素过多,不利于单独分析放宽静稳定的作用;另一种是固定焦点位置,后移重心位置,这种方式理论分析简便,且在实际运用中的重心控制也可通过改变配重或燃油转输的方式较为方便地实现。
本文在前人研究的基础上,采用第二种放宽静稳定度的方法,针对某型先进战斗机,通过建模仿真,研究放宽静稳定度对飞机纵向的俯仰力矩总力矩系数、平衡点、开环收敛特性、阶跃特性、模态特性的影响。
1 战斗机非线性数学模型
数学模型建模假设:地球呈平面且不旋转,飞机为刚体、质量恒定且沿中垂面对称(飞机的惯性积I
=I
=0),不考虑发动机进动效应。从飞机受力情况出发(如图1(a)所示),构建平衡方程。本文默认焦点位置在0.348 处,选取重心位置x
在 0.26~0.40 区间,如图 1(b)所示。
图1 重心和焦点位置Fig.1 The position of barycenter and neutral point
1.1 气动参数计算及分析
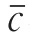

C
、总侧向力系数C
、总升力系数C
、总滚转力矩系数C
和总偏航力矩系数C
的具体表达式,其具体形式详见文献[24]。根据式(1),通过重心后移分析放宽静稳定度对某型战斗机的纵向静稳定特性的影响,如表 1 和图 2~图 5 所示(δ
=0°、δ
=0°、β
=0°、q
=0°)。
表1 放宽静稳定度飞机纵向稳定性分析Table 1 Analysis of longitudinal stability of aircraft with relaxed static stability
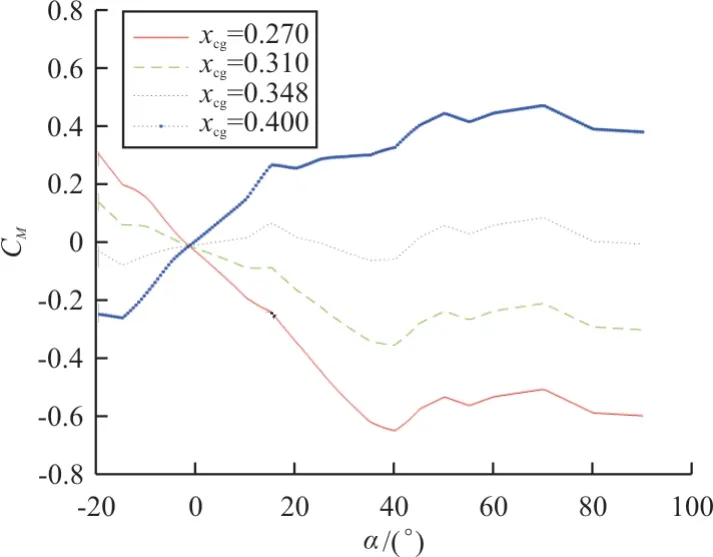
图2 α 和 xcg 变化对 CM 的影响Fig.2 α and xcg change the effect on CM

图3 α =0 时,δe 和 xcg 变化对 CM 的影响Fig.3 α=0,δe and xcg change the effect on CM

图4 δe=25°时,α 和 xcg 变化对 CM 的影响Fig.4 δe=25°,α and xcg change the effect on CM

图5 δe=-25°时,α 和 xcg 变化对 CM 的影响Fig.5 δe=-25°,α and xcg change the effect on CM
从图2 可以看出:在攻角小于约40°时,C
与α
近似呈线性关系,之后趋近于定值。在参考重心位置x
=0.35 时,只有满足攻角α
大于 0 时,俯仰气动力矩系数C
小于 0;攻角α
小于 0 时,总俯仰气动力矩系数C
大于0,飞机才为完全的纵向静稳定。随着重心位置后移,俯仰气动力矩系数C
愈发难以满足上述静稳定条件,在x
为0.27、0.31时,飞机在任意攻角下都能实现俯仰稳定;在x
=0.35 时,飞机只能在攻角为40°附近时才能勉强不借助操纵面实现俯仰力矩的配平;x
=0.4 时,飞机为完全的静不稳定,俯仰力矩系数在正攻角情况下恒大于0,即受到抬头扰动时,无法自动产生低头力矩进行平衡,反而增大的力矩系数会产生抬头力矩,进一步加速攻角增大,直至大攻角完全失速。从图3 可以看出:总俯仰气动力矩系数C
会随着重心位置x
后移、随着升降舵偏转角δ
增大而减小,即逐渐产生更大的低头俯仰力矩。从图4 可以看出:在图2 的基础上将升降舵偏转角δ
设为正值上限25°,相比图2 相同攻角情况下,俯仰力矩系数明显减小,面对抬头扰动飞机的可用控制低头力矩明显增加。因此飞机能通过升降舵偏转角δ
有效提供俯仰稳定,防止飞机受到抬头扰动后,无法自动恢复以致达到极端攻角。但襟副翼同向偏转角δ
能提供的最大可用俯仰力矩有限,当重心位置x
过分后移,即稳定度过于放宽,大量可用俯仰力矩被维持俯仰稳定所占用,势必对飞机的俯仰机动能力产生不良影响。从图5 可以看出:当受到低头力矩扰动(α
<1°),也能通过升降舵低头产生抬头控制力矩进行调节。1.2 某型战斗机非线性数学模型的建立

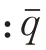
由于飞机在惯性坐标系中运动,绝对加速度为牵连加速度、相对加速度和科氏加速度的矢量和。根据实际情况忽略掉科氏加速度,可得飞机投影到体坐标系各方向上的加速度为
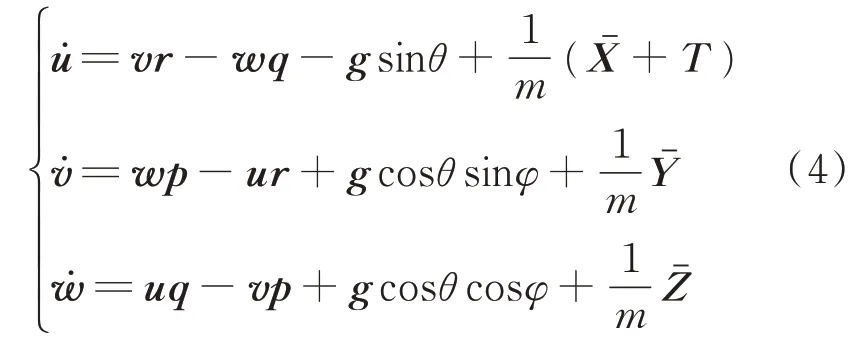
T
为发动机推力,其可描述为油门杆开度δ
的非线性函数,由于篇幅限制,在此省略其具体描述过程。为了方便建模时函数调用和数据插值,将体坐标系的速度分量v
、u
、w
转换为气流坐标系的总速度V
、攻角α
、侧滑角β
来描述速度大小及方向的变化: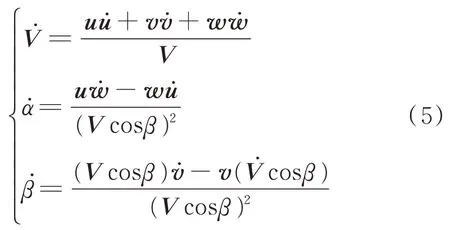
再根据动量矩定理可推导出:

I
、I
、I
为对应体坐标系各轴的惯性矩;I
为相对于x
-y
和y
-z
平面的惯性积。


1.3 放宽静稳定度对非线性数学模型开环特性的影响
为进一步分析重心及放宽静稳定度对先进战斗机开环特性的影响,在不同的重心和初始条件下(V
=150 m/s、α=0、θ
=0、q
=0、X
=0、Z
=-2 000 m),对所建立的非线性数学模型进行开环仿真分析,具体如表2 和图6~图7 所示。
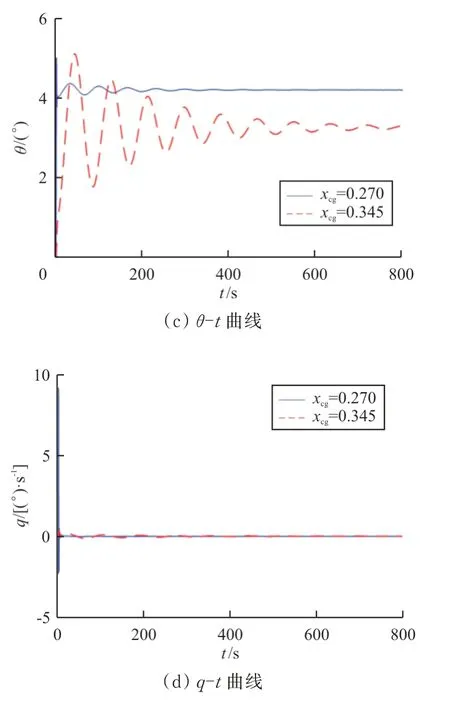
图6 xcg分别为0.270 和0.345 时,适度放宽静稳定性的非线性模型开环特性曲线Fig.6 xcg=0.270 and xcg=0.345,the open loop characteristic curve of nonlinear model with moderate relaxation of static stability

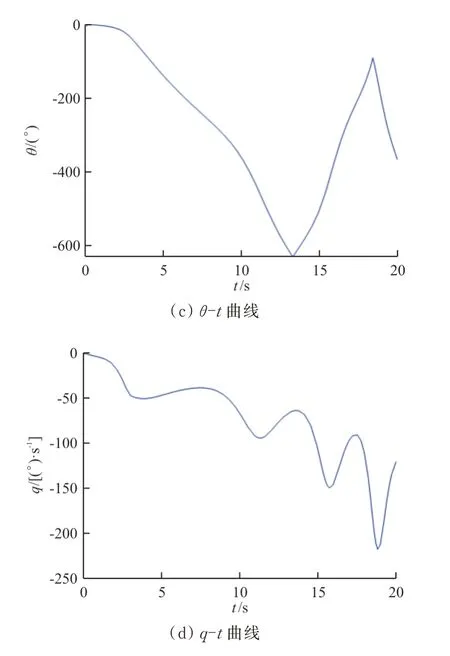
图7 xcg=0.36 时,完全放宽静稳定性的非线性模型开环特性曲线Fig.7 xcg=0.36,the open loop characteristic curve of nonlinear model with complete relaxation of static stability

表2 放宽静稳定度飞机非线性数学模型开环特性Table 2 Open loop characteristics of nonlinear mathematical models of aircraft with extended static stability
从图6 可以看出:当x
=0.345 时,虽然适当放宽静稳定度后,飞机仍能够收敛到平衡点附近,但相比于x
=0.27 时,受重心位置后移的影响,收敛时间明显变长,且振幅增大。从图7 可以看出:由于重心位置已经后移越过焦点,飞机已无法在开环条件下稳定飞行,飞行状态完全发散,需要采取增稳控制。
2 放宽静稳定度对非线性模型平衡点的影响
2.1 飞机非线性数学模型的运动配平

图8 飞机纵向配平参数Fig.8 Aircraft longitudinal trim parameters
2.2 飞机配平点特性受到放宽静稳定的影响
配平条件为2 000 m 海拔高度水平直飞,利用上述优化配平函数trim 以及仿真模型调用函数sim,对重心位置x
从0.26 到0.34(战斗机在该区间都为静稳定状态),飞行总速度V
从100 到250 m/s 范围内的配平点进行等距采样(如图9 所示)。在纵向平面内分析,飞机的俯仰力矩可分为由机身产生的俯仰力矩和升降舵产生的俯仰力矩两部分,前者主要受攻角影响,后者主要受升降舵偏角影响。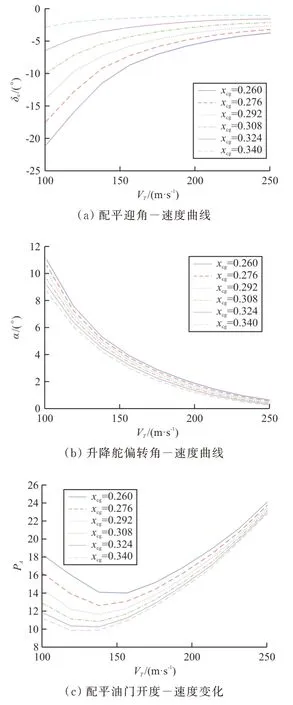
图9 放宽静稳定度对飞机平衡点的影响Fig.9 Influence of relaxing static stability on aircraft equilibrium point
从图9(a)可以看出:当速度恒定,重心后移时,在保持静稳定情况下,重心越来越接近焦点,所产生的扰动力矩减小,平衡所需的力矩系数也减小,随之配平攻角越接近0。
从图9(b)可以看出:配平所需升降舵偏角随重心位置后移有逐渐增大的趋势,若采集重心位置后移越过焦点之后(飞机静不稳定状态)的数据,所需升降舵偏角会变为正值且数值随之进一步增加。这主要是由于在飞机静稳定时,重心在焦点之前,升力绕重心产生的机身俯仰力矩对飞机整体形成低头的效果,升降舵面需要通过低头(升降舵偏转角为负),产生向下的气动力,从而生成绕重心使飞机抬头的力矩与机身俯仰力矩进行配平;当飞机静不稳定后,重心移到焦点之后,机身产生的俯仰力矩变为抬头力矩,升降舵面又需要通过抬头(升降舵偏转角为正),产生向上的气动力,进而生成绕重心使飞机低头的力矩与机身俯仰力矩进行配平。这个过程为连续过程,故随着重心的向后移动(数值增大),升降舵偏角也会从正值到负值逐渐增大,图9(b)只展示了飞机在静稳定状态下随重心位置变化的规律。
从图9(c)可以看出:推力随着重心位置后移而逐渐减小,在低速下尤其明显。这是由于图9(a)中,随着重心位置的后移,攻角随之减小,产生的阻力系数减小,对低速时的阻力影响更明显。同时,由于升降舵偏角对阻力也有一定的影响。又因如图3 所示,在飞机保持静稳定条件下,升降舵偏角随重心位置后移增大趋近于0,也进一步减小了阻力系数,从而使推力随重心位置后移的减小变化更加明显。
综上所述,随着纵向静稳定性的放宽,飞机保持定速直飞状态飞行所需的升降舵偏角、攻角和推力都会减小。这样就减小了定速直飞阻力,进而减小了巡航耗油率,变相增加巡航半径,又留出更多的可用控制俯仰力矩,提高了飞机的机动性能。
3 战斗机的纵向线性模型放宽静稳定的特性分析
3.1 纵向运动线性模型
本文仅考虑飞机纵向运动,输入参数的向量u
=[δ
δ
]。输出为包含4 个参数的向量y
=[V α θ q
]。利用配平函数trim 获得在设定重心位置处的纵向配平点x
。再针对获得配平点x
,利用线性化函数linmod 获得将上述建立的飞机纵向非线性数学模型转换为飞机纵向小扰动线性化方程
A
、B
、C
、D
为所需的雅可比矩阵。在海拔高度h
=2 000 m、飞行速度v
=150 m/s 条件下,选取三个有代表性的重心位置(0.270、0.345、0.350)分析飞机纵向线性数学模型的油门杆阶跃响应和升降舵响应特性。通过线性化函数linmod 获得各重心位置对应的雅可比矩阵A
、B
、C
、D
,其 中A
和B
如 表 3 所 示 ,C
=I
,D
=O
:
表3 各重心位置对应的雅可比矩阵A 和BTable 3 Jacobian matrices A and B corresponding to each barycenter position
3.2 放宽静稳定度对阶跃响应特性的影响
为进一步分析放宽静稳定度对飞机性能的影响,在不同重心位置下分别给油门杆和升降舵施加阶跃信号,以便直观的显示速度、攻角、俯仰角、俯仰角速度在阶跃响应下的特性曲线,如图10~图11 所示。

图10 xcg 分别为 0.270 和 0.345 时,飞机线性模型对 δth 的阶跃响应曲线Fig.10 xcg=0.270 and xcg=0.345,step response curve of a linear aircraft model to δth
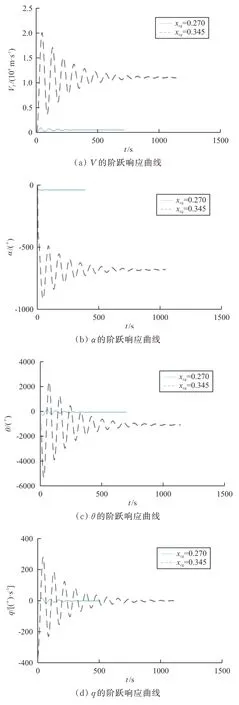
图11 xcg 分别为 0.270 和 0.345 时,飞机线性模型对 δe 的阶跃响应曲线Fig.11 xcg=0.270 and xcg=0.345,step response curve of a linear aircraft model to δe
从图10~图11 可以看出:以升降舵偏角为输入的传递函数阶跃响应相比于油门杆开度都有更大的最大超调量和更长的调节时间。重心位置为0.270 与0.345 时,重心位置仍在焦点之前,只是x
=0.345 非常接近焦点,虽也保持了传递函数的收敛性,最大超调量发生了数量级倍数的增大,调节时间也有明显的延长,收敛性显著减弱。当重心位置后移越过焦点到达0.35 时,如图12~图13 所示,可以看出:以油门杆和升降舵阶跃输入得到的响应表现出单调增加或减小的特性,说明相应的传递函数完全发散,飞机纵向线性小扰动模型受到扰动时无法再靠自身回到初始配平位置,呈现完全的静不稳定。
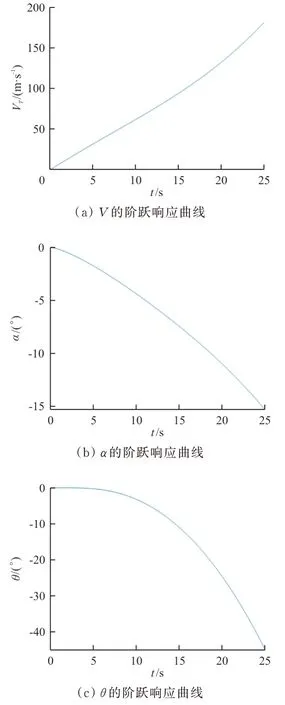
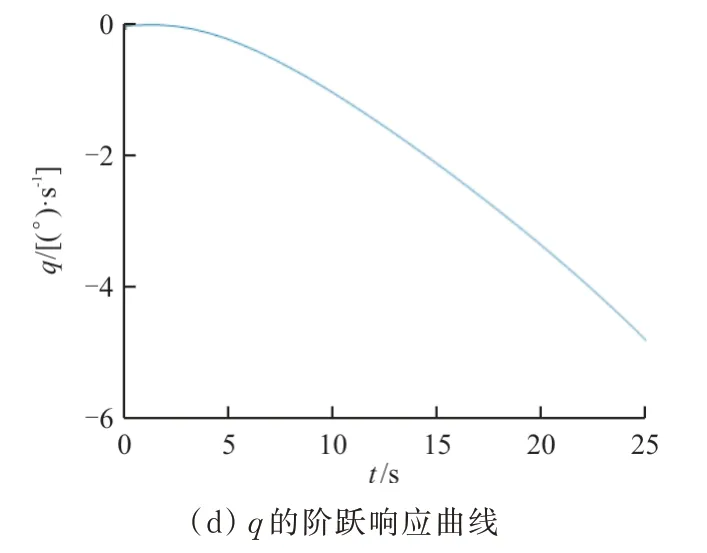
图12 xcg=0.35 时,飞机线性模型对δth 的阶跃响应曲线Fig.12 xcg=0.35,step response curve of a linear aircraft model to δth
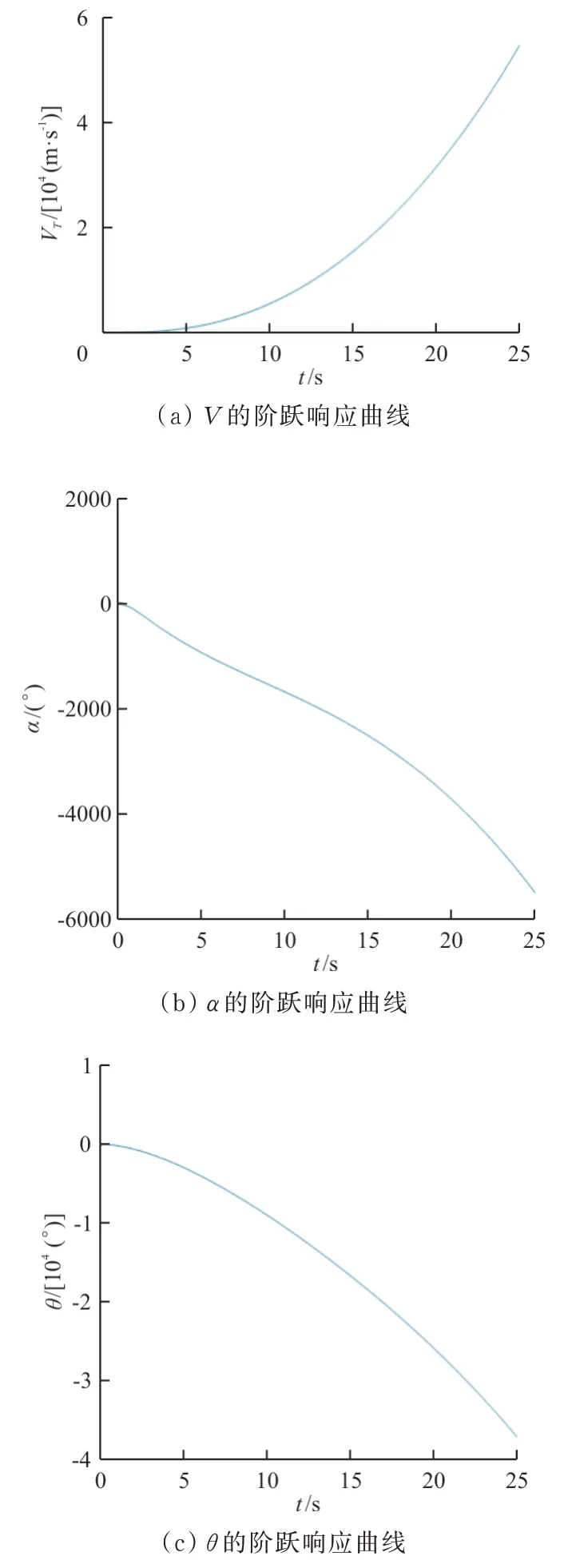

图13 xcg=0.35 时,飞机线性模型对δe 的阶跃响应曲线Fig.13 xcg=0.35,step response curve of a linear aircraft model to δe
3.3 放宽静稳定度对飞机纵向运动模态特性的影响
小扰动方程矩阵的四个特征根呈两组共轭复根形式,分别代表长周期模态和短周期模态。通常长周期模态对应的共轭复根数值相对较小,其模态特性为振动周期长、衰退慢,主要影响飞机速度变化,飞行员易于进行手动控制;而短周期模态对应的共轭复根数值相对较大,其模态特性为振动周期短、衰退快,主要影响飞机姿态变化,飞行员手动操作存在延时性的问题,很难实时调节,对操作品质影响更大。
两个典型运动的模态特性主要通过无阻尼固有频率W
、阻尼比ζ
和周期T
三个参数来描述。短周期模态周期短不易人工控制,因此短周期阻尼比ζ
是描述飞机稳定性特性的关键。短周期阻尼比ζ
过大会使飞机对操纵指令反应迟缓,不利于操作;而ζ
过小又会使飞机受扰易产生长时间、大幅度的振荡。利用damp 函数可获得两种经典模态的模态特性随静稳定度放开的变化,如表4 和图14所示。

图14 两典型运动模态无阻尼固有频率Wn、阻尼比ζ、周期T 随稳定度放宽的变化Fig.14 Variation of undamped natural frequencyWn,damping ratio ζ and period T with relaxation of stability of two typical motion modes

表4 不同重心位置的长、短周期模态特征值Table 4 The long and short period mode eigenvalues of different barycenter positions
从表4 可以看出:飞机的长周期和短周期共轭复根随重心后移都有相互靠拢且接近实轴的趋势,短周期相符靠拢的趋势更明显,长周期趋近实轴更加明显,这也表明两种模态的稳定性都在下降。
从图14 可以看出:随重心向后移动(从0.26到0.34),无阻尼固有频率W
逐渐减小(长周期从0.087 5 到 0.081 7,短周期从 2.167 3 到 1.441 4),周期T
逐渐增大(长周期从69.671 7 到77.002 4 s,短周期从1.622 7 到5.728 5 s),表明两种模态受扰后振荡持续时间都会明显延长;同时,随重心向后移动,长周期阻尼比逐渐减小(从0.094 3 到0.056 6),短周期阻尼比逐渐增大(从0.396 4 到0.648 8),进一步表明飞机纵向小扰动模型运动模态恶化。4 结 论
(1)先进战斗机总俯仰力矩系数随静稳定放开而增大,飞机本体模态可能变得静不稳定,但在特殊攻角和速度条件下,仍存在自稳定可能。主动控制需对这些特殊点进行考虑。
(2)飞机非线性模型的配平点特性随着静稳定度放宽呈较平稳的连续变化。可以用该性质实现静稳定和非静稳定状态的平滑切换。
(3)不仅放宽静稳定对飞机动态特性有明显的影响,初始平衡点选择也会在一定程度上改变仿真结果,需要谨慎地选取初始平衡点。

